标题里面的名词在后续的学习中频繁的出现,这里就做了一些总结,应该是没有什么错误的了,然后这段内容用例子来讲也没有多大的意思,数学抽象的苦该吃还得吃。
先来醒醒脑看上一眼
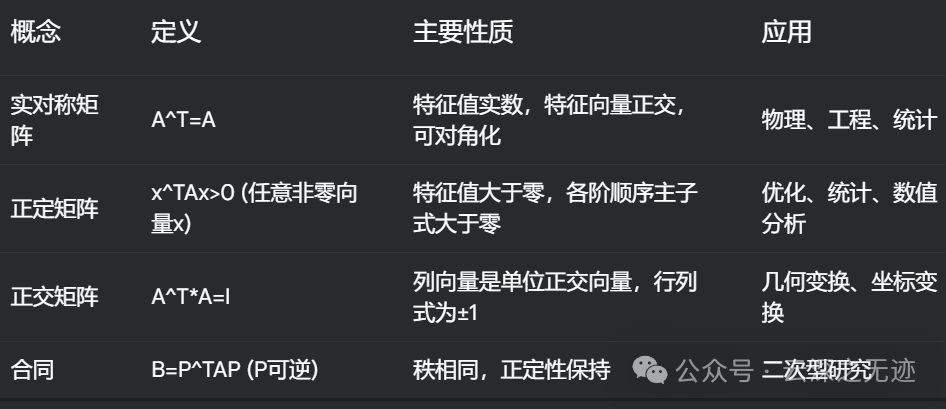
正交矩阵是线性代数中一类特殊的方阵。
如果一个方阵A满足:
A^T * A = A * A^T = I其中,A^T表示矩阵A的转置,I为单位矩阵,那么矩阵A就被称为正交矩阵。
旋转: 正交矩阵可以表示空间中的旋转变换。想象一个坐标系,经过正交矩阵变换后,坐标轴的位置会发生旋转,但原点和坐标轴之间的相互关系不变。
其实最出名的正交矩阵就是旋转变换中的:
| cosθ -sinθ || sinθ cosθ |
可以算这个的行列式,等于一,某种程度上面也可以回答为什么右上角的系数是负一。
列向量(或行向量)是单位正交向量:正交矩阵的每一列(或每一行)都是单位向量,且两两相互垂直。
行列式为1或-1:正交矩阵的行列式值要么是1,要么是-1。
逆矩阵等于转置矩阵:正交矩阵的逆矩阵就是它的转置矩阵。就因为这条性质才会有了矩阵的N次方的求解办法
保持向量长度不变:正交矩阵作用于一个向量后,向量的长度不会改变。
保持向量之间的夹角不变:正交矩阵作用于两个向量后,这两个向量之间的夹角不会改变。
实对称矩阵是指一个矩阵的转置等于其本身,且所有元素都是实数的方阵。也就是说,对于一个n阶矩阵A,如果满足A^T = A,且A中的所有元素都是实数,那么A就是一个实对称矩阵。
| 2 1 || 1 3 |
特征值均为实数:实对称矩阵的所有特征值都是实数。
特征向量相互正交:对应不同特征值的特征向量相互正交。
可对角化:实对称矩阵一定可以对角化,且存在一个正交矩阵P,使得P^TAP为对角矩阵,对角线元素即为矩阵的特征值。
实对称矩阵表示的是一个二次型。二次型在几何上对应于一个二次曲面。实对称矩阵的特征值和特征向量可以确定这个二次曲面的形状、大小和方向。
正定矩阵是实对称矩阵的一个子集。如果一个实对称矩阵的所有特征值都大于零,那么它就是一个正定矩阵。它的行列式大于零,所有主子式都大于零。

放图是为了让你看下面的子式概念
其实这个子式啥的频繁出现,一直也没有理解,这里补充一下。
主子式(principal minor)是指从一个方阵中选取相同行和相同列所构成的子矩阵的行列式。换句话说,就是从一个方阵的对角线开始,选取连续的几行几列,所形成的子矩阵的行列式。
顺序主子式:从矩阵的左上角开始,依次取1×1、2×2、...、n×n的子矩阵的行列式。
主子式:更一般地,从矩阵中任意选取k行k列(行号和列号相同),所形成的子矩阵的行列式。
| 1 2 3 || 4 5 6 || 7 8 9 |
顺序主子式:1,|1 2| | 4 5|,|1 2 3| | 4 5 6| | 7 8 9|,其实就是主对角线开始选择,顺序在主对角线的元素上面。
主子式:除了顺序主子式外,还有|2 3| | 5 6|,|1 3| | 4 6| 等。注意这个主子式其实就是任意选择,但是约束在于行列是相等的,也就是一个方形的矩阵。
在回答下面这个问题前:线性代数后记-对角化到施密特正交化
答案:是的,一定。
可以拆开研究,首先实对称矩阵:一个矩阵的转置等于其本身,且所有元素都是实数的方阵;正交相似化:将一个矩阵通过一个正交变换转化为对角矩阵的过程。
实对称矩阵的特征值:实对称矩阵的所有特征值都是实数。
实对称矩阵的特征向量:实对称矩阵的不同特征值对应的特征向量是相互正交的。
正交矩阵的构造:将实对称矩阵的所有特征向量单位化后,按列组成一个矩阵,这个矩阵就是正交矩阵。
对于一个实对称矩阵A,总能找到一个正交矩阵Q,使得Q^TAQ是一个对角矩阵,对角线上的元素就是A的特征值。这个过程就是实对称矩阵的正交相似对角化。
在合同和正定之间应该先说正定,因为前面的铺垫容易引入这个。
正定矩阵(Positive Definite Matrix)它本质上描述了一种特殊的二次型,即对于任意非零向量x,二次型x^TAx的值总是正的。
设A是一个n阶实对称矩阵。如果对于任意非零向量x∈R^n,都有:
x^TAx > 0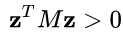
还有写法是这样的,注意M或者A都是实对称矩阵
则称矩阵A为正定矩阵。(接上文)
其中,
x^T表示向量x的转置。
x^TAx是一个标量,代表向量x经过矩阵A的线性变换后得到的新的向量与原向量x的内积。
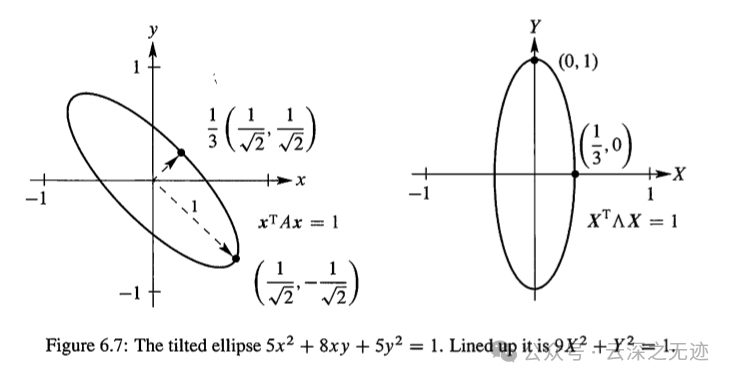
这个东西太抽象了,我找了一个图
从几何角度看,正定矩阵对应的是一个椭球。这个椭球的形状和大小由矩阵A的特征值和特征向量决定。所有的特征值都是正的,表明这个椭球的各个轴的长度都是正的,且没有退化的情况。
实际上,它里面的判定是最重要的:
所有特征值都是正的:这是正定矩阵的一个重要特征。
行列式大于零:正定矩阵的行列式一定是正的。
所有主子式都大于零:主子式是指矩阵中包含对角线元素的所有子矩阵的行列式。
存在唯一的Cholesky分解:即可以分解为一个下三角矩阵L和其转置L^T的乘积,且L的对角线元素都是正的。
具体的计算方法就是:
特征值法:计算矩阵的所有特征值,若所有特征值均为正,则矩阵为正定。
顺序主子式法:计算矩阵的所有顺序主子式,若均为正,则矩阵为正定。
合同变换法:将矩阵化为对角矩阵,若对角线元素全为正,则矩阵为正定。
二次型法:根据定义,对于任意非零向量x,计算x^TAx,若结果恒大于零,则矩阵为正定。
因为在这里的话,正定和实对称都说了,那他们的联系呢?
正定矩阵是实对称矩阵的一个子集。如果一个实对称矩阵的所有特征值都大于零,那么它就是一个正定矩阵。
正定矩阵的行列式大于零,所有主子式都大于零。
剩下就是一个合同了,在二次型里面时不时的出现:
定义: 对于两个 n 阶矩阵 A 和 B,如果存在一个可逆矩阵 P,使得:
B = P^T * A * P我这个写的不好看,看下面的:

其实这里需要补充一点,合同不是矩阵,而是矩阵之间的一种关系,称为合同,公式里面也表明了这一点。
那么称矩阵 A 和 B 合同。这里,P^T 表示矩阵 P 的转置。(接上文)
可以把合同矩阵看作是对同一个二次型进行了不同的线性变换。就像一个物体,从不同的角度去看,它的形状可能不同,但本质上还是同一个物体。
对称性: 如果 A 是对称矩阵,那么与 A 合同的矩阵 B 也一定是对称矩阵。
秩不变性: 合同矩阵具有相同的秩。
正定性: 如果 A 是正定矩阵,那么与 A 合同的矩阵 B 也一定是正定矩阵。
所有与单位矩阵合同的对称矩阵都是正定矩阵。
相似矩阵:要求存在可逆矩阵 P,使得 B = P^-1 * A * P。这里的P是逆矩阵
合同矩阵:要求存在可逆矩阵 P,使得 B = P^T * A * P。这里的是什么?是转置。
相似矩阵主要用于研究矩阵的特征值和特征向量,而合同矩阵主要用于研究二次型和矩阵的正定性,
假设有矩阵 A 和 B:
A = [[1, 2], [2, 4]]B = [[5, 0], [0, 1]]
如果我们能找到一个可逆矩阵 P,使得 B = P^T * A * P,那么 A 和 B 就是合同的。
这里的话就都总结好了,然后就是再来补充一些缺掉的知识。
我们频繁的说明喜欢对角矩阵,说下为啥喜欢,其实就是爱在它的性质,数学上面的努力其实是为了大一统和可计算性。
对角矩阵是一种特殊的方阵,它的特点是:除了主对角线上的元素外,其他所有元素都为0。
| 2 0 0 || 0 3 0 || 0 0 -1 |
对称矩阵:对角矩阵一定是对称矩阵。
上三角矩阵:对角矩阵也是上三角矩阵。
下三角矩阵:对角矩阵也是下三角矩阵。
单位矩阵和零矩阵都是特殊的对角矩阵。
对角矩阵的特征值就是主对角线上的元素。
对角矩阵的行列式就是主对角线上的元素的乘积。
加法和减法:同阶对角矩阵的加法和减法就是对应元素相加减。
数乘:用一个数乘以对角矩阵,就是将对角线上的每个元素都乘以这个数。
乘法:两个对角矩阵的乘法,得到的仍然是一个对角矩阵,且对角线上的元素是对应元素的乘积。
包括以前写的施密特正交化其实也是在蹭对角矩阵的光。
还有一种矩阵叫,正交相似矩阵,其实我只是在一个评论区看到的。正交相似变换是一种特殊的相似变换,它在保持矩阵特征值不变的同时,还具有保留对称性、简化矩阵等性质。
相似变换: 对于两个方阵A和B,如果存在可逆矩阵P,使得B = P^(-1)AP,那么称矩阵A和B相似。相似变换保持矩阵的特征值不变。
正交变换: 一个正交矩阵Q满足Q^TQ = QQ^T = I,其中I是单位矩阵。正交变换保持向量长度和向量之间的夹角不变。
正交相似变换就是指,如果存在一个正交矩阵Q,使得B = Q^TAQ,那么称矩阵A和B正交相似。
对称矩阵的对角化: 任意一个实对称矩阵都可以通过正交相似变换对角化。这是因为实对称矩阵的特征向量是相互正交的,可以构成一个正交矩阵。
奇异值分解(SVD): SVD是将矩阵分解为三个矩阵的乘积,其中两个是正交矩阵。
继续问,那正交相似矩阵一定合同吗?
我的回答是不一定。
我回答这种问题以前,是会先问自己,里面的名词的数学含义是什么?
合同的定义:对于两个n阶方阵A和B,如果存在一个可逆矩阵P,使得B = P^TAP,则称矩阵A和B合同。合同关系反映了两个矩阵在某种线性变换下的等价性。
正交相似的定义:对于两个n阶方阵A和B,如果存在一个正交矩阵Q,使得B = Q^TAQ,则称矩阵A和B正交相似。正交相似是相似的一种特殊情况,变换矩阵Q是正交的。
也就是说:正交相似是相似关系的一个子集,而相似关系是合同关系的一个子集。正交相似矩阵一定是相似矩阵,而相似矩阵不一定合同。
正交矩阵Q是可逆的,但不是任意可逆矩阵。因此,满足正交相似关系的矩阵不一定满足合同关系的任意可逆变换。
正交相似是比合同更强的条件,满足正交相似的矩阵一定相似,但未必合同。
小小的总结一下:正交相似就像用一个特殊的镜子去看一个物体,这个镜子不会改变物体的形状,只会改变它的方向。而合同则像用一个任意形状的透镜去看一个物体,可能会改变物体的形状。
正交相似是相似关系的一个特例,它要求变换矩阵是正交矩阵。实对称矩阵具有特殊的性质,它的特征向量是相互正交的,因此可以被正交相似对角化。合同是一个更广义的概念,它要求变换矩阵是可逆的。

今日封面
https://m.sohu.com/a/667524147_348129/?pvid=000115_3w_a