

计算机中通过高低电平表示1或者0,这样就可以表示一个二进制的数值。一个1或者0表示的数值位称为一个bit,而计算机中存储和传输数据的最小单位是一个字节(byte)也就是8个bit,所以说计算机所有计算本质上都是基于二进制。
在计算机中,我们可以使用1个或者多个字节存储一个数,但无论是多少个字节,其大小肯定是固定的,同时其所能表示的数值的范围也是固定的。比如说对使用1个字节存储的数进行计算或者传输,那么这个数所能表示的最小值为00000000最大值为11111111,转换为十进制为0 ~ 255。那么无论对这个数做了什么计算,无论计算之后的结果为多少都不能超出这个范围,同理使用2个字节存储的数范围为0 ~ 65535。
由于很多时候一个数据需要使用2个或者2个以上的字节表示,那么这种数据无论是存储还是传输的时候都会有一个顺序的问题,也就是大小端对齐(字节序)问题。在存储时高位字节在前为大端对齐,反之为小端对齐。在数据传输时先传输高位字节为大端字节序,反之为小端字节序。目前绝大多数平台内部都是小端对齐的方式存储数据,而大多数通信协议却都是用大端字节序传输数据,所以这一点值得注意一下。


计算机中使用二进制存储传输和计算数值,但是不能只有数值,计算的时候还得有正负之分。在计算机中使用最高bit位的数值来表示正负号,这个bit位称作符号位。
计算机中符号位的值为0表示这个数为正数,符号位值为1表示这个树为负数。由于符号位表示符号所以其不表示具体的值,除开符号位剩余的bit位用来表示数值也就是数值位。比如1个字节的整数00000001,其中最高bit(最左边)位的0为符号位,表示这个数为正数,数值位为1,所以其真值为1。同理2个字节的整数00000000_0000001,其真值也是1。


计算机只识别机器码,其实也就是二进制数,并且使用最高bit位表示符号位。那么两个真值为8和-8的8位整数,它们在计算机内部的机器值是否就分别是00001000和10001000?其实并不是,这只是8和-8的原码,而机器算计中的机器值是使用补码存储和计算的。
计算机中,正数的原码、反码和补码是一样的,所以上面那个例子中,真值为8的8位整数的机器值确实是00001000,但是-8就不是这么回事了。负数的首先将原码数值位按位取反得到反码,然后再将反码数值位加1之后则得到补码。我们来看一下-8这个例子,其原码为10001000,数值位按位取反之后的反码为11110111,然后数值位加1之后的补码为11111000。所以真值为-8的8位整数在计算机中的机器值为11111000,我们来看下面这张表:
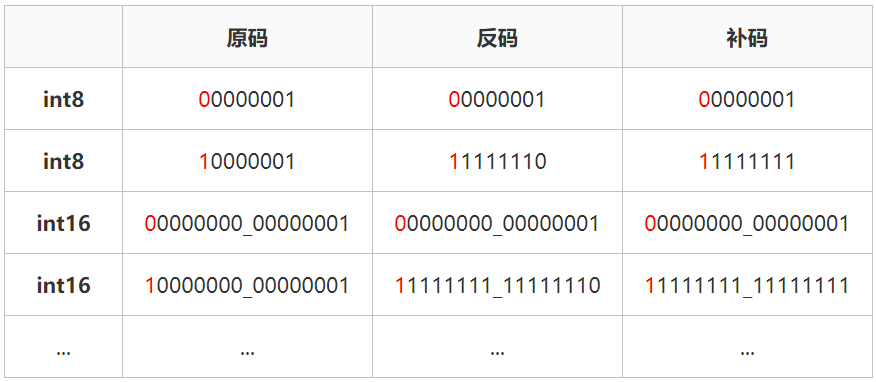
注:int8为8bit位整数占用1byte,int16为16bit位整数占用2byte。
刚说的是原码转补码的步骤,其实补码转原码的步骤是一样的。首先正数的原码补码是一样的不需要转换,我们看负数11111000,首先将数值位按位取反得到10000111,然后再将数值位加1得到10001000。我们再来看一个8位的整数10000000,是不是发现这个数原码和补码是一样的,那么这个看起来像是“-0”的数是怎么回事呢?其实可以将这个数看成是一个特殊值,它的真实含义就是最小值。8位的这种“-0”的真值为-128,16位的这种“-0”真值为-32768。所以只需要记住100...000这种补码就是最小值就行,我们看下面的这张表:
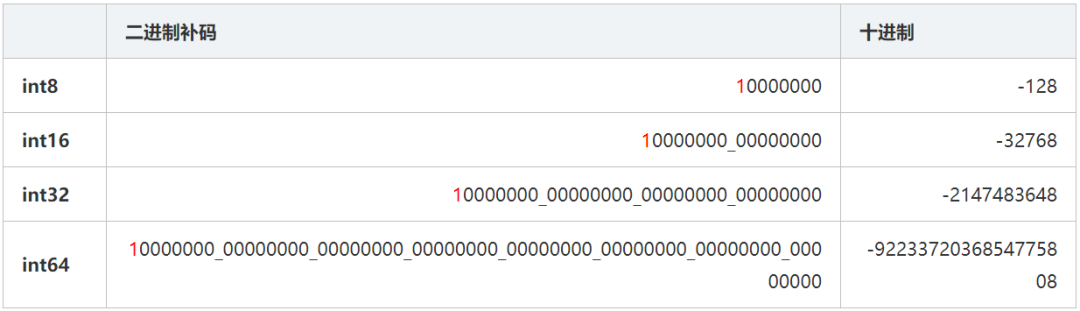
有两对8bit位的整数4、8和4、-8,我们分别看一下他们在计算机中是怎么做加法计算的。首先看4和8的补码分别为00000100和00001000,只需要将每个bit位相加就行,结果为00001100,其真值为12。我们再来4和-8的计算,它们补码分别为00000100和11111000,然后将它们按位相加(注意符号位也要做加法)得到11111100,其原码为10000100,真值为-4。
再来看一下减法计算,比如8bit位的整数-8减去4,首先可以将4处理一下可以变为(-8) + (-4),这样是不是就又变为了加法了?-8和-4的补码分别为11111000和11111100,将它们按位相加得到补码11110100(注意这是8位的整数,超出部分发生了溢出),转换成原码为10001100,真值为-12。
再来看一下乘法,比如8bit位的整数-8乘以13,他们的补码分别为11111000和00001101。其中-8为被乘数,13为乘数,并且乘数有8个bit位,需要将被乘数按位与和位计算8次然后将结果相加,看如下分析:
被乘数的第0个bit位值为1,将被乘数乘以1然后左移0位得到:11111000;
被乘数的第1个bit位值为0,将被乘数乘以0然后左移1位得到:00000000;
被乘数的第2个bit位值为1,将被乘数乘以1然后左移2位得到;11100000;
被乘数的第3个bit位值为1,将被乘数乘以1然后左移3位得到;11000000;
被乘数的第4个bit位值为0,将被乘数乘以0然后左移4位得到;00000000;
被乘数的第5个bit位值为0,将被乘数乘以0然后左移5位得到;00000000;
被乘数的第6个bit位值为0,将被乘数乘以0然后左移6位得到;00000000;
被乘数的第7个bit位值为0,将被乘数乘以0然后左移7位得到;00000000;
由此可以得计算得到8组补码(注意上面做位移涉及到的整数溢出,只能是8个bit位),然后将它们做加法得到10011000(也存在整数溢出)转换为原码为11101000,真值为-104。
至于除法则是使用交替加减法的方式,本文只是对计算原理做一下扩展,这里不再继续深入做介绍,如果有想了解的可以自行上网查询。
通过上面的分析可以知道,使用补码可以将所有计算都转化为加法计算,这样可以让计算机底层对于整数计算变得简单,反码属于历史遗留,因为其存在±0的问题。
节选自《二进制小总结》
https://www.cnblogs.com/lbole/p/14260496.html
成功为华为“续命:中国芯片之父张汝京
这位“华为天才少年”,竟然要我用“充电宝”打《只狼》