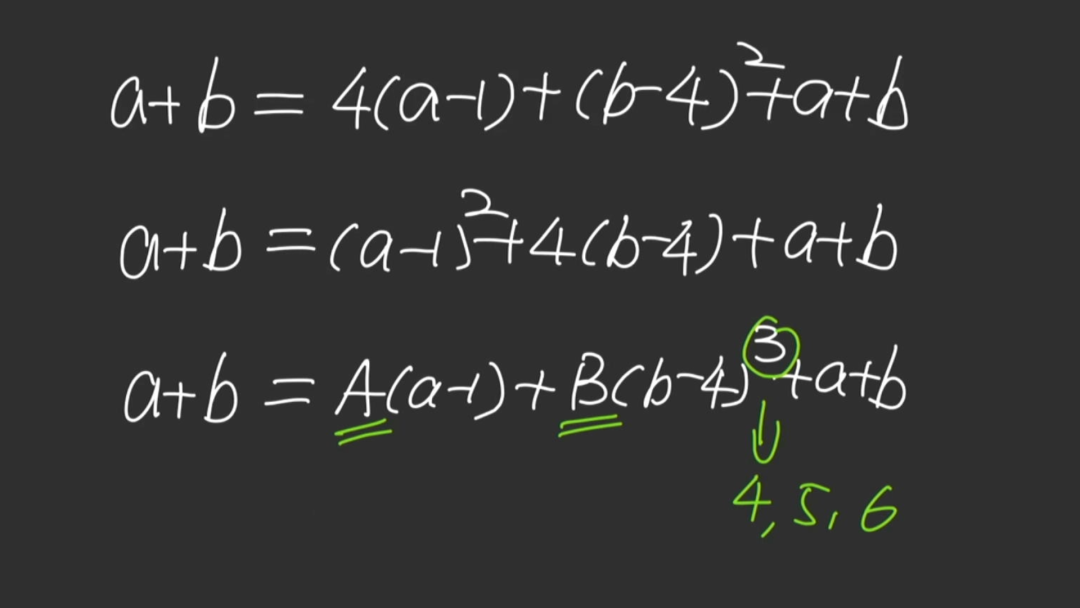这里有六个数字,他们排成三行,构成三个加法表达式,这里给出了运算结果。这就奇怪了,是是不是喝多了 ? 因为只有第一个表达式结果是正确的。后面两个是错误的。如果让你重新定义表达式中的加号对应的运算,让这三个表达式都是正确的。请你写出最后一个运算表达式的结果,那么它应该是多少呢?
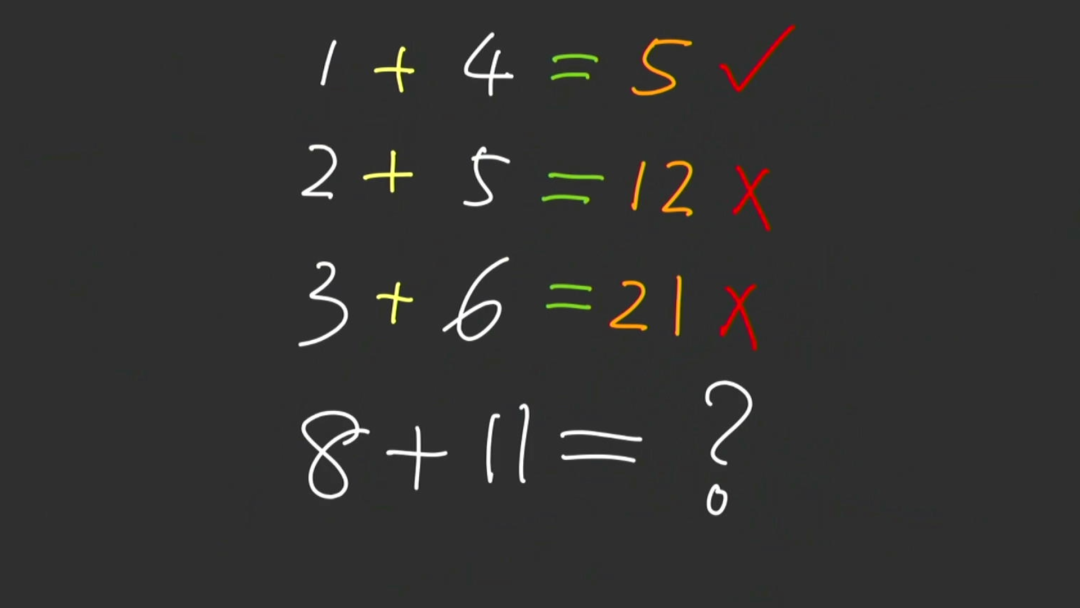
有位老兄给重新给出了加号的运算,为了使得三个表达式都成立,定义加号运算等于第一个数字加上两个数字的乘积。 可以验证,这样的定义,三个表达式都成立。由此,最后一个表达式的值 应该等于96。这位老兄真的是一个天才。
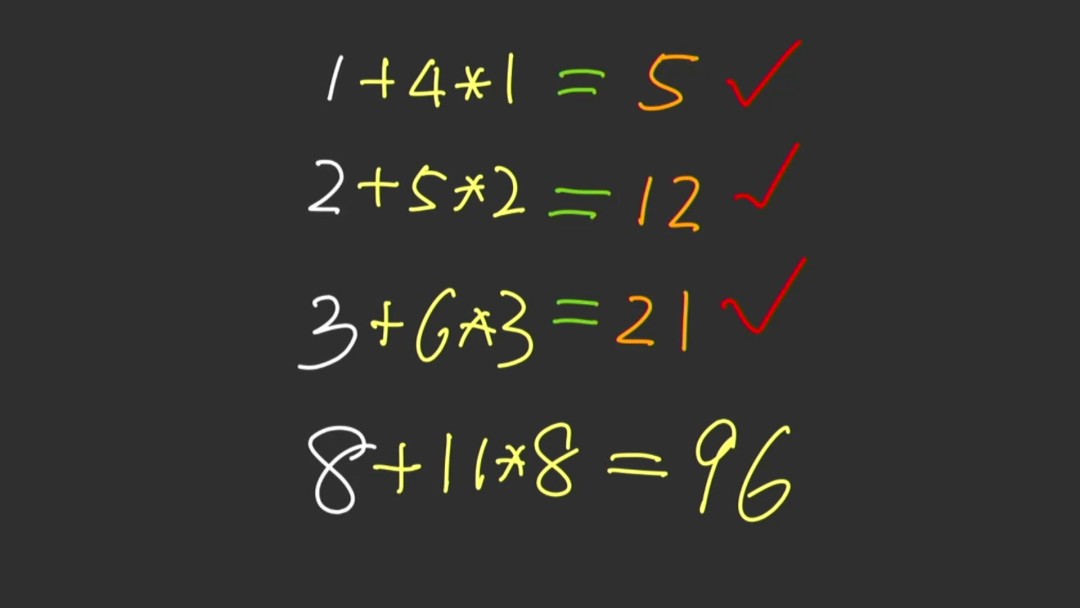
不过,问题来了。除了这个答案之外,是否还有其他的规律,能够使得前面三个表达式成立吗? 又有一位大聪明,给出了他的想法,从第二个表达式开始,都将前面的表达式的结果叠加起来,这样便可以得到正确的结果。验证第三个表达式,诚不我欺也,结果也同样适用。好了,按照这个规律,我们可以给出最后一个表达式的计算值,那就是 等于40。对于这两种方式你觉得哪一个更加有趣呢?
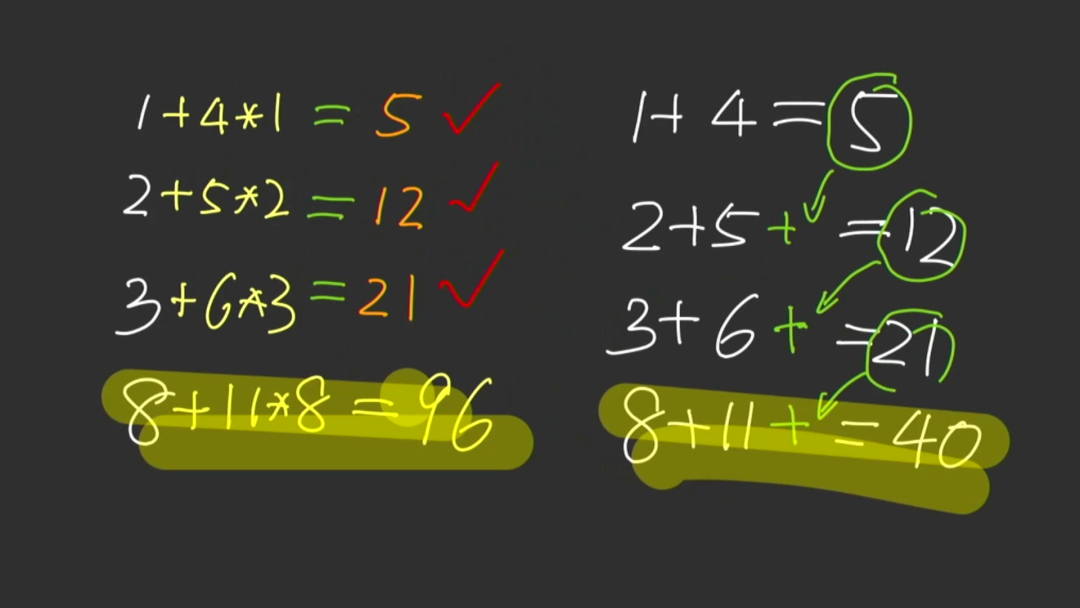
下面,我们尝试一下,看是否能够搜索到其他的加法定义,也能够使得前面三个表达式成立。第一个表达式是正确的。第二个表达式多出了5,第三个表达式多出了12 。
我们假设,着多出来的数字与前面参与相加的两个数字有关系。比如,等于它们对应一个二次多项式。其中大A,大B是待定系数。那么,根据前面三个表达式, 我们可以列出三个等式。通过这三个等式,最终求出待定系数A、B 分别为4 和 1。下面我们来 验证一下是否正确。 先以第三个表达式为例,将它的加号重新书写成下面对应的表达式,可以看到的确等于21.对于第二个表达式,根据同样的运算方式,也可以得到对应的结果。 最开始的表达式,结果也是正确的。这就是根据前面三个表达式,最终给出的加号的运算内容。下面,将其作用在第四个表达式上, 可以看到,它对应的数值,等于96。这里有趣的是,这个数值实际上与第一种给出的答案是相同的。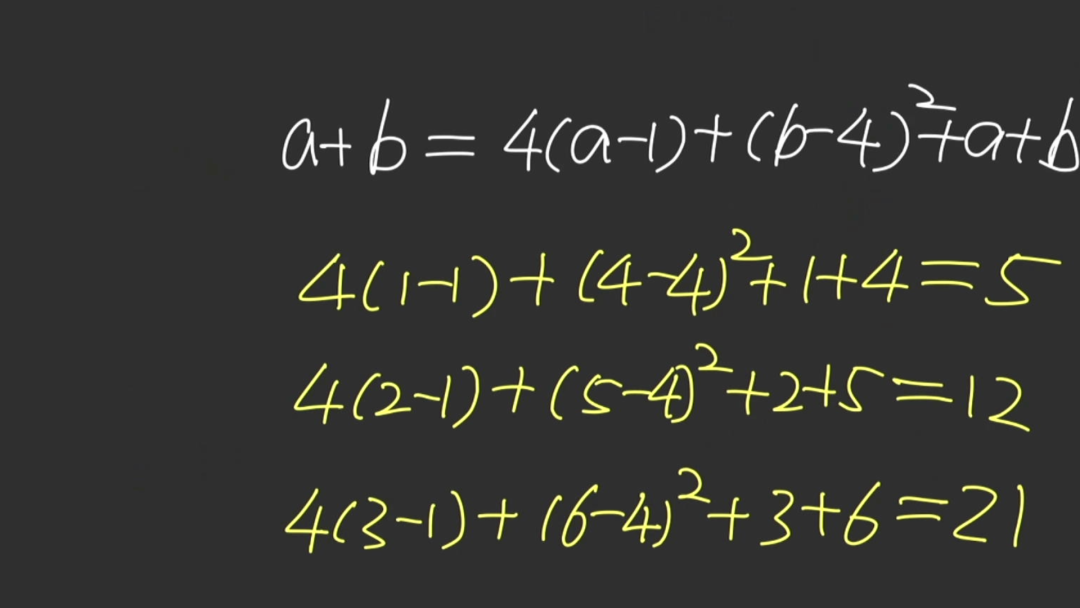
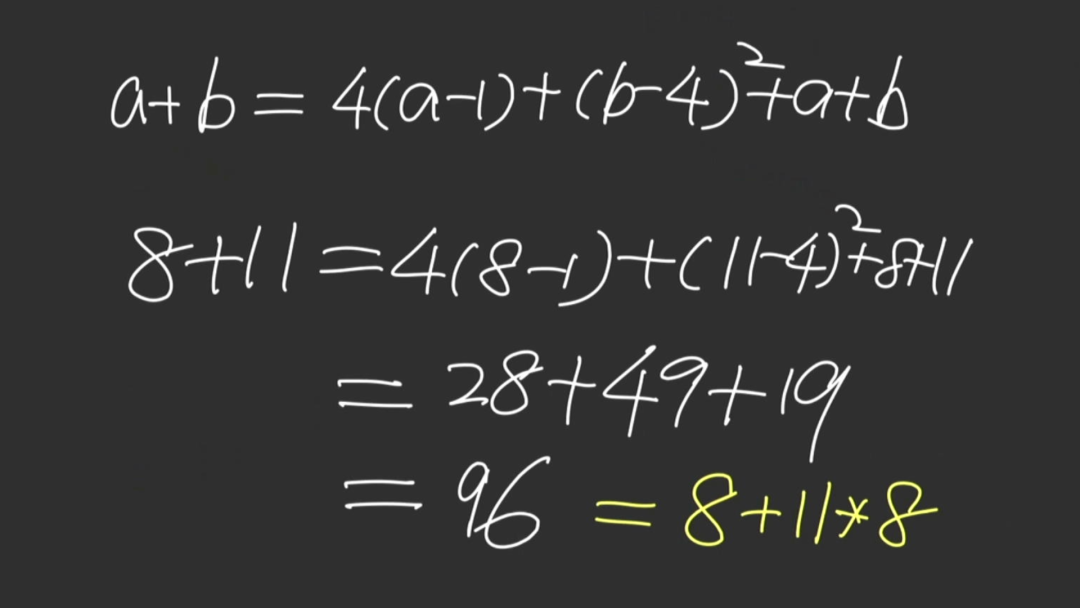
根据前面的分析,我们可以知道,还有一种对称的定义表达式,同样也可以满足前面三个表达式。对应的,也可以写出无穷多个这种表达式。只是对应的A,B参数有所不同。只要改变这里的指数,从平方改成立方,四次方,等等。实际上可以写出无穷多种能够是的前面表达式成立的定义。