对于一个LTI系统,当其初始状态为零时,输入为单位冲激函数δ(t),所引起的响应称为单位冲激响应,简称冲激响应。通常用h(t)表示。
线性性: 这意味着系统满足叠加原理和齐次性。简单来说,就是当多个输入信号同时作用于系统时,系统的总输出等于每个输入单独作用时产生的输出之和。
时不变性: 这意味着系统的特性不随时间的推移而改变。也就是说,无论何时对系统施加相同的输入,得到的输出总是相同的。
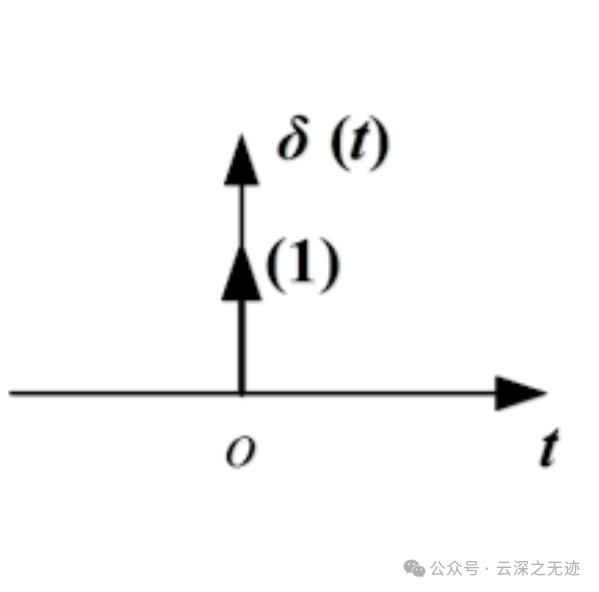
注入能量
冲激响应h(t)包含了LTI系统的所有信息。换句话说,只要知道一个系统的冲激响应,就可以完全确定这个系统的特性。
对于任意输入信号x(t),系统的输出y(t)可以通过输入信号x(t)与冲激响应h(t)的卷积来得到:
y(t) = x(t) * h(t)微分方程法: 将单位冲激函数δ(t)作为输入,代入系统的微分方程,求解得到的输出即为冲激响应。信号与系统-时域分析-微分方程求解.茅塞顿开版
a_n * y^(n)(t) + a_(n-1) * y^(n-1)(t) + ... + a_1 * y'(t) + a_0 * y(t) =b_m * x^(m)(t) + b_(m-1) * x^(m-1)(t) + ... + b_1 * x'(t) + b_0 * x(t)
通过对微分方程进行拉普拉斯变换,可以得到系统的传递函数。传递函数是描述LTI系统输入输出关系的另外一种方式。
拉普拉斯变换法: 将系统的微分方程进行拉普拉斯变换,得到传递函数H(s),然后对H(s)进行逆拉普拉斯变换,即可得到冲激响应h(t)。
冲激响应的物理意义:
系统的固有特性: 冲激响应反映了系统对一个瞬时扰动的响应,因此它反映了系统的固有特性,如系统的振荡特性、衰减特性等。
系统对不同频率信号的响应: 冲激响应的傅里叶变换就是系统的频率响应,它表示系统对不同频率信号的放大倍数和相移。
