建议是先看一遍这个文章-小张带你看看信号与系统三大变换(骂骂咧咧版)
然后再来读这篇,本来文章就回答一个问题,但是后面就又变成了拉普拉斯变换的学习笔记,不影响哈,早晚都得学。
初学的时候就在想,为什么是e^st这个形式,有没有别的?(现在也回答不好)

如果看不懂文章的可以看祖师爷的原文
其实最一开始的起因是连续时间傅里叶变换,而这些东西都是从周期到非周期的推广:
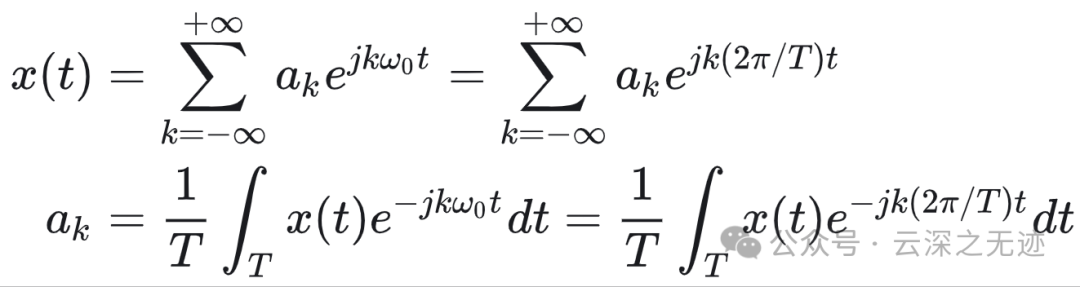
这是周期信号
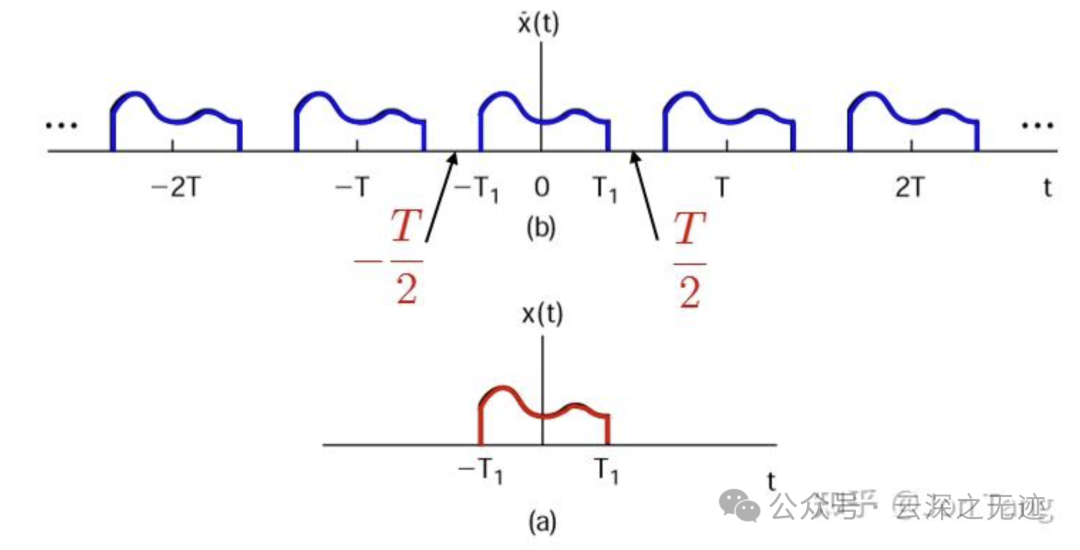
通过把一个信号当成一个周期信号在周期任意大时的极限来看待。这是信号与系统的半壁江山的想法,也是从周期到非周期,走向泛化的想法。
我这里啰里啰唆是想提醒读者包括自己,这门学科公式繁复,靠背诵是不可取的,要深刻的理解推理过程,最好的教科书是重建理论构建之路。
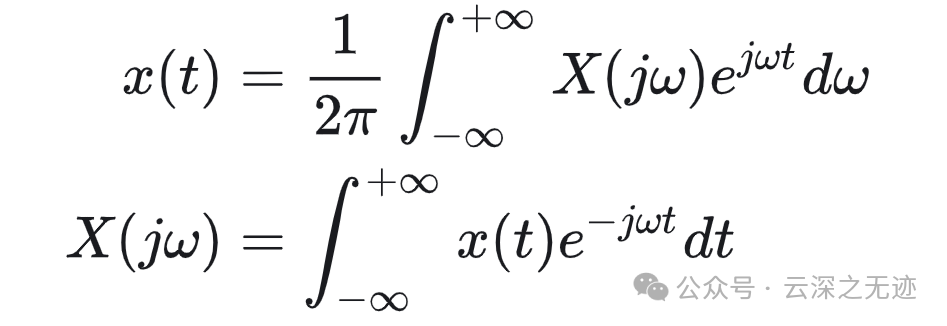
这就是非周期的连续时间傅里叶变换
事实上,这个东西离拉普拉斯的变换已经很接近了。拉普拉斯变换可以看作是傅里叶变换的推广。傅里叶变换将一个函数分解成不同频率的正弦波的叠加。然而,傅里叶变换对函数的收敛性有一定要求,即函数必须满足一定的条件(如绝对可积)。然而,许多实际信号,如阶跃函数、斜坡函数等,并不满足这个条件。许多原本不满足绝对可积条件的函数在乘上这个因子后变得可积,从而保证拉普拉斯变换的积分收敛。
为了克服傅里叶变换的限制,我们引入一个衰减因子e^(-σt),其中σ是一个实数。这个衰减因子可以使一些增长过快的函数在乘上这个因子后变得可积。
衰减因子看作是一个随着时间逐渐减小的权重。对于那些增长过快的函数,随着时间的推移,其乘上衰减因子后的值会越来越小,最终使得积分收敛。
F(s) = ∫[0,∞] f(t) * e^(-st) dte^(-σt): 衰减因子,控制信号的衰减速率。
e^(jωt): 复指数信号,表示信号的频率成分。
复数s同时包含了信号的幅值和相位信息,可以统一表示时域信号和频域信号。
s = σ + jωσ 是s的实部,代表信号的衰减或增长速率。
j 是虚数单位,j² = -1。
ω 是s的虚部,代表信号的频率。
等等!这里要讨论啦,我们说衰减一定是速度很快的停下来。
底数大于1的情况:
自变量趋向正无穷: 指数函数的值会趋向于正无穷。
自变量趋向负无穷: 指数函数的值会趋向于0。
自变量趋向某个具体值: 指数函数的值会趋向于一个确定的常数。
底数在0到1之间的情况:
自变量趋向正无穷: 指数函数的值会趋向于0。
自变量趋向负无穷: 指数函数的值会趋向于正无穷。
自变量趋向某个具体值: 指数函数的值会趋向于一个确定的常数。
我是感觉这样可以在数学上面说明,因为S就是一个复函数,也就是有具体的值,那么最后就可以趋向于一个确定的常数。
衰减项e^(-σt): 这里的s是一个复数,可以表示为s = σ + jω。实部σ决定了信号的衰减速率。当σ>0时,信号随时间指数衰减;当σ<0时,信号随时间指数增长;当σ=0时,信号幅值保持不变。这是上面我说的内容
振荡项e^(jωt): 虚部jω则引入了频率的概念。e^(jωt)表示一个频率为ω的复指数信号,它在复平面上绕原点旋转。
e^(-st) 这个函数将时域信号的衰减和振荡特性统一起来,映射到复频域
首先是数学性质优良:指数函数具有良好的微积分性质,便于进行微分和积分运算。因为信号与系统最重要的就是卷积了,求响应,里面不可避免的有卷积积分,积分我们不好积啊!自然界中许多现象都可以用指数函数来描述,例如放射性衰变、电路中的RC电路等。e^(-st) 的导数仍然是e^(-st) 的倍数,这使得微分方程的求解变得简单。
二是频域分析的需要: 通过乘以e^(-st)并积分,我们可以将时域信号分解成不同频率的成分,从而在频域进行分析。这个也好理解,对系统的分析就是把一个输入的信号分解成正交的简单信号然后在LTI系统下进行变换。e^(jωt) 表示一个复指数信号,它包含了信号的频率信息。
三系统的输入输出关系: 在线性时不变系统中,输入信号的拉普拉斯变换与系统的传递函数的乘积等于输出信号的拉普拉斯变换。这里说的是特征函数。
衰减因子: e^(-σt) 可以看作是一个衰减因子,它描述了信号随着时间衰减的快慢。
旋转因子: e^(jωt) 可以看作是一个旋转因子,它描述了信号的振荡特性。
复频域: s是一个复数,它包含了信号的幅度和频率信息。

今日封面