这是一个周期锯齿波行,周期为 2π,幅度为 π,关于原点为奇对称。它的傅里叶级数,可以通过一个周期内的积分计算而得。
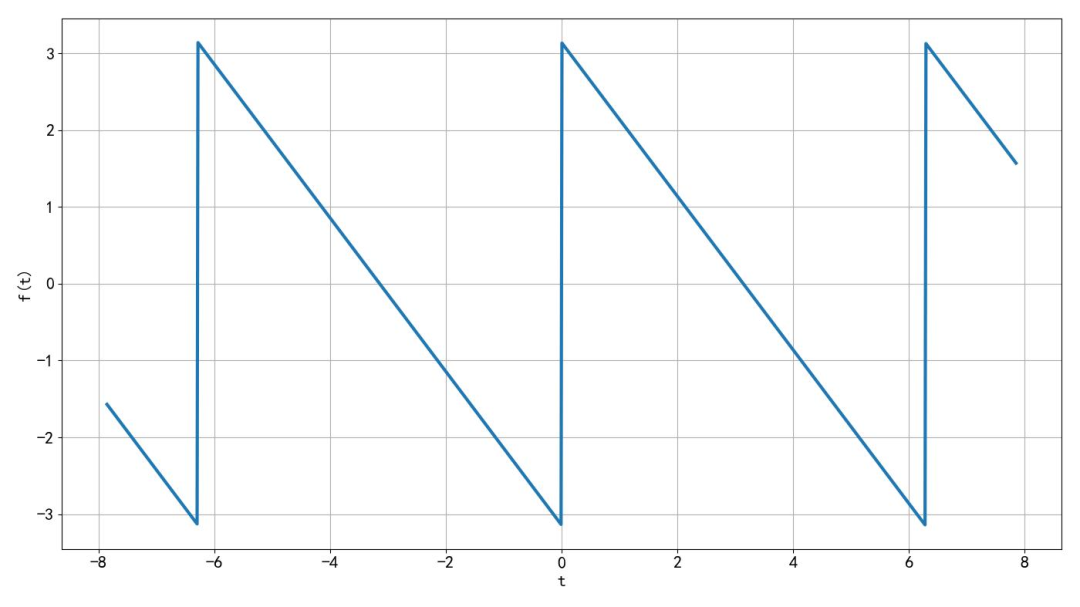
▲ 图1.1.1 周期锯齿波形这个积分分为两项。前面这部分,是周期信号正周期内的积分,取值为 0。后面积分项,可以通过分部积分进行计算。将指数部分移到微分项内。根据分部积分法,分为两项,后面部分的积分仍然为 0。前面这部分,经过计算,它的取值为 j n 分之一。
由此,可以得到周期锯齿波的傅里叶级数分解的形式。如果将他乘以 j,变成纯虚信号。对应的级数分解的形式更加简洁。下面,我们利用这个公式,绘制有限项傅里叶级数叠加的信号。
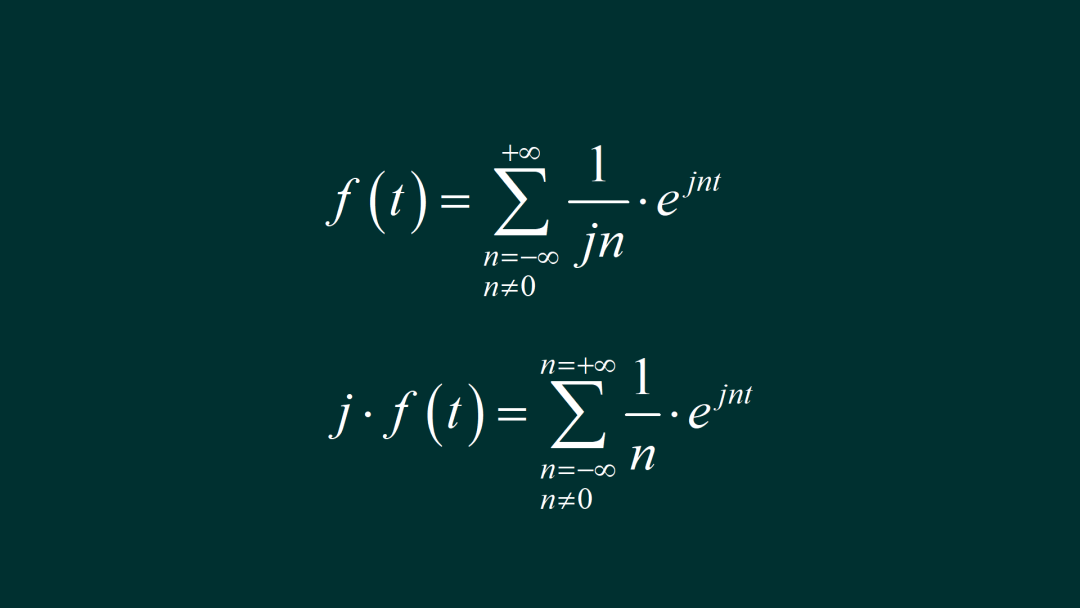
二、有限项傅里叶级数之和
将小于 N 之内的谐波进行叠加,可以获得原来信号的近似波形。这个叠加结果是一个纯虚信号。如果将右边一半进行叠加,所获得的信号是一个复数信号。这里绘制钱100项的叠加结果,由于信号与吧间断点。叠加信号在间断点前后有过冲。这个过冲的赋值随着叠加项数的增加,逐步趋向于一个常熟。并不衰减。这个现象被称为吉布斯现象。
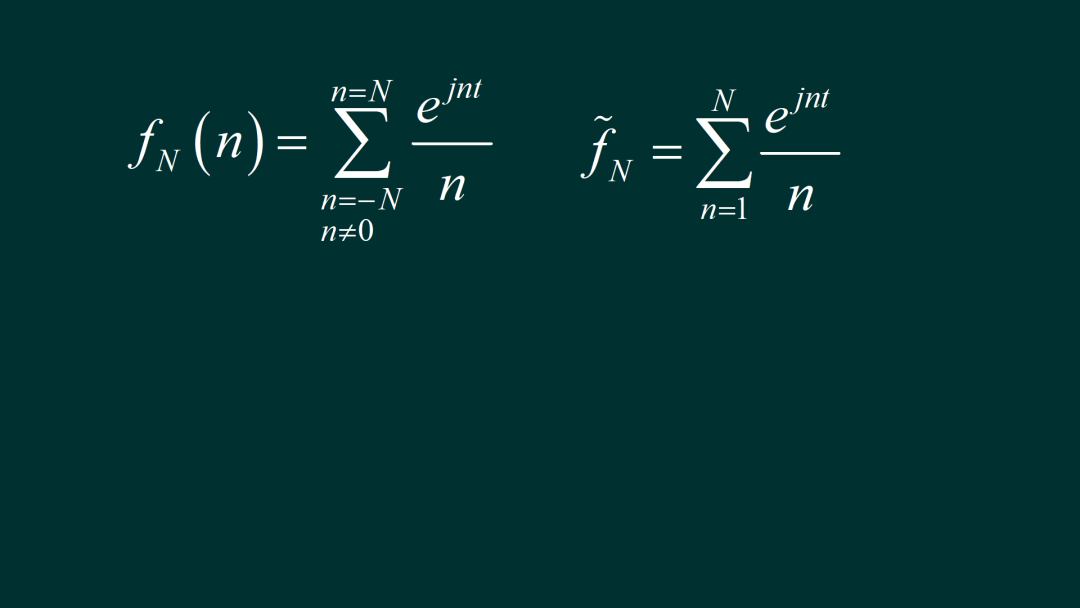
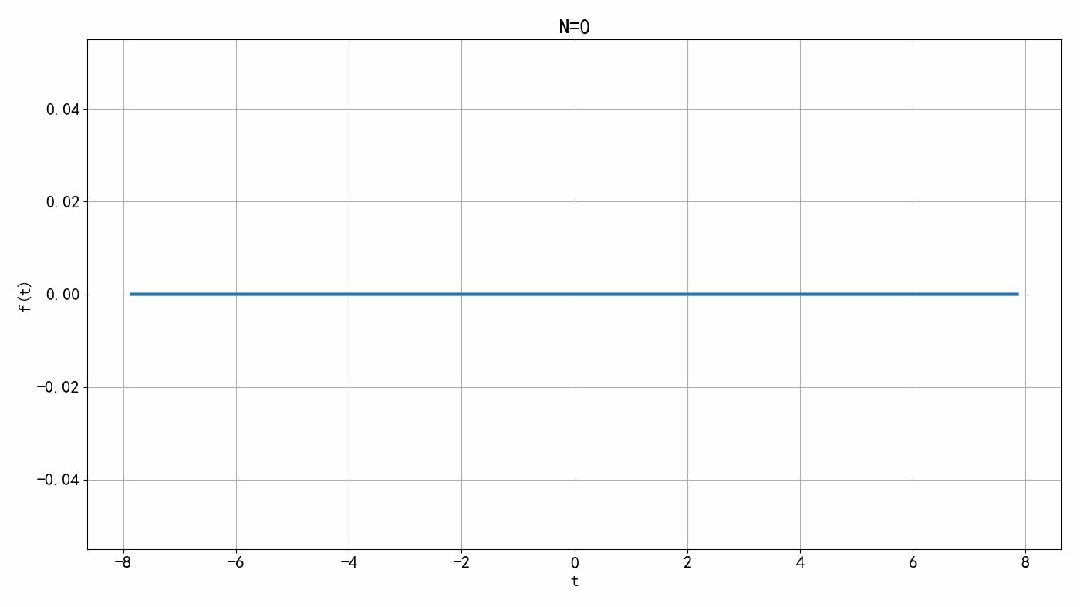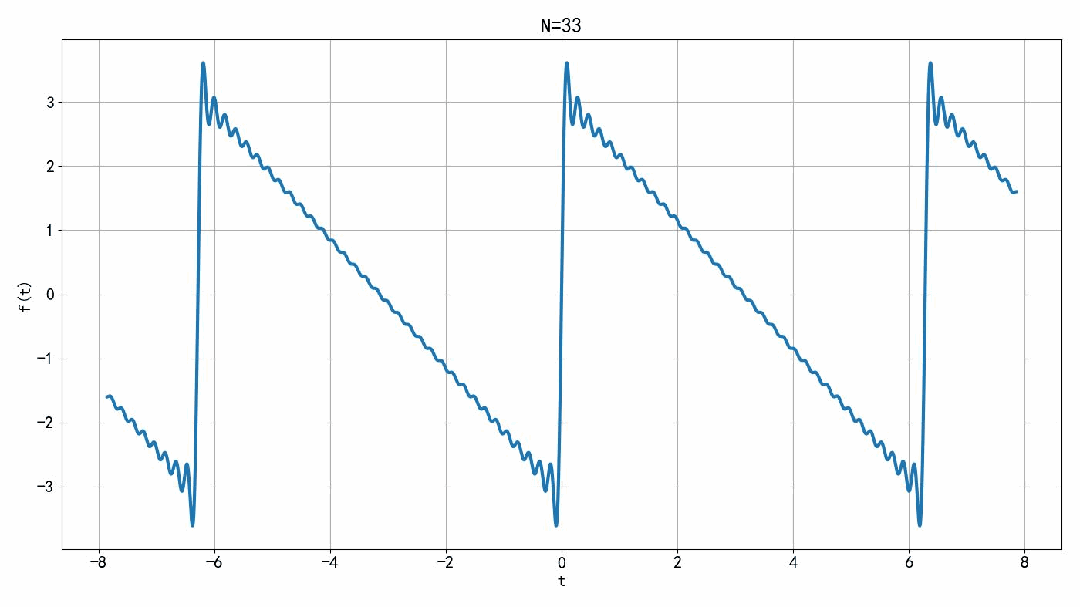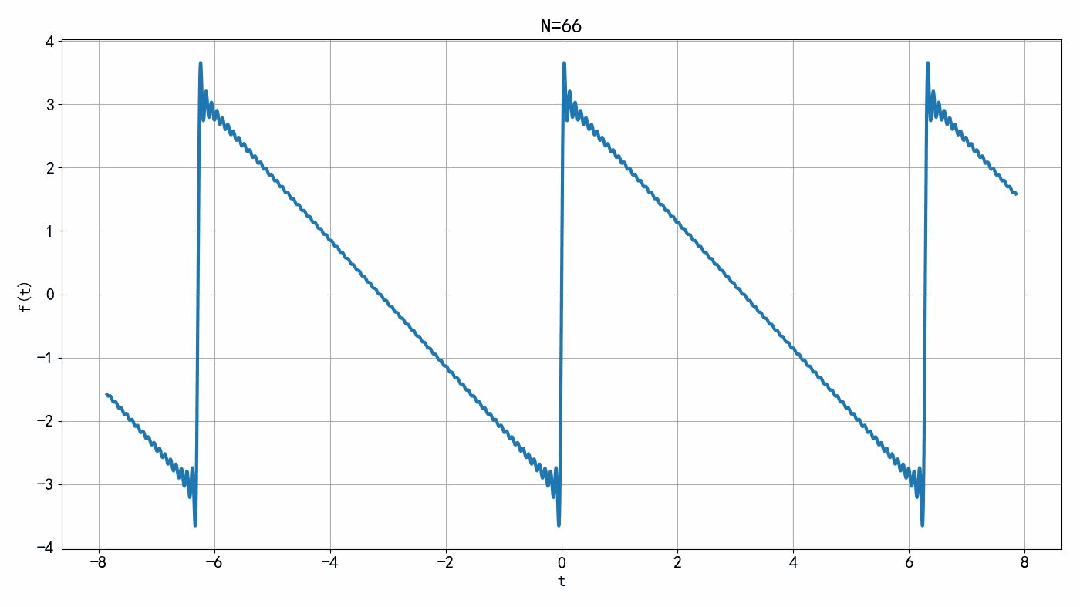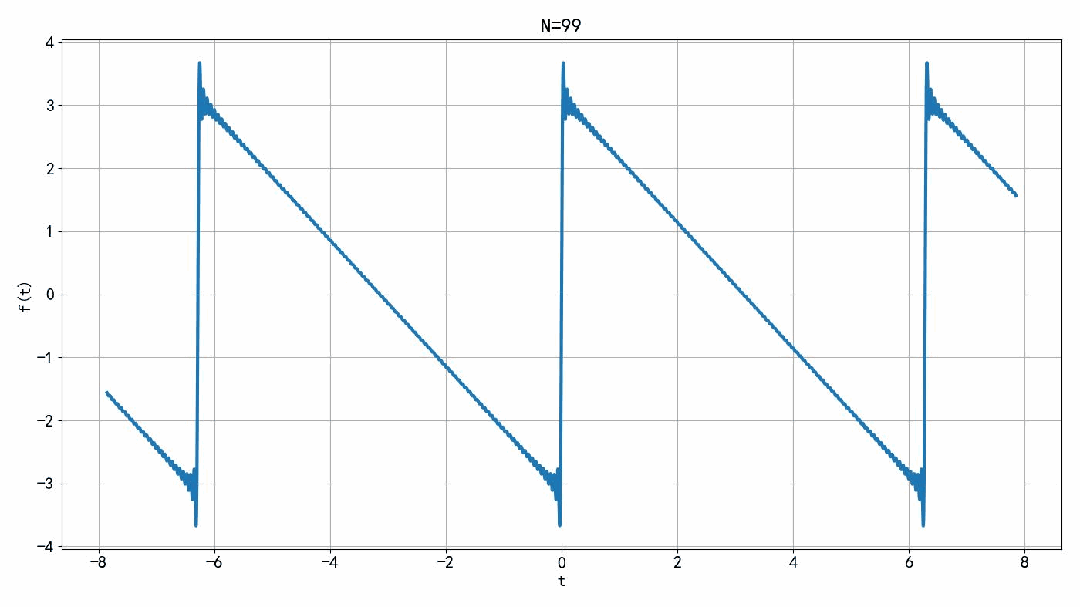
▲ 图1.2.1 前N项傅里叶级数叠加后的结果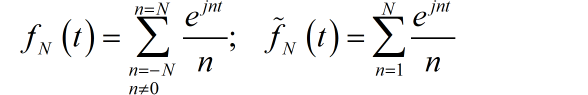
下面,分别绘制出半边有限项傅里叶级数叠加的实部和虚部。虚部是锯齿波的一半。实部,似乎在 t=0 处的幅度一直在增加,虽然增加的速度越来越慢,但究竟是会收敛,还是会发散呢? 根据定义, 在 t=0 处,随着项数趋向于∞,叠加信号的实部会发散。 由此我们可以看到,如果是双边有限项的叠加,在 t=0 处,信号会收敛。但是如果叠加半边的有限项傅里叶级数,在 t=0 处,信号居然会发散。
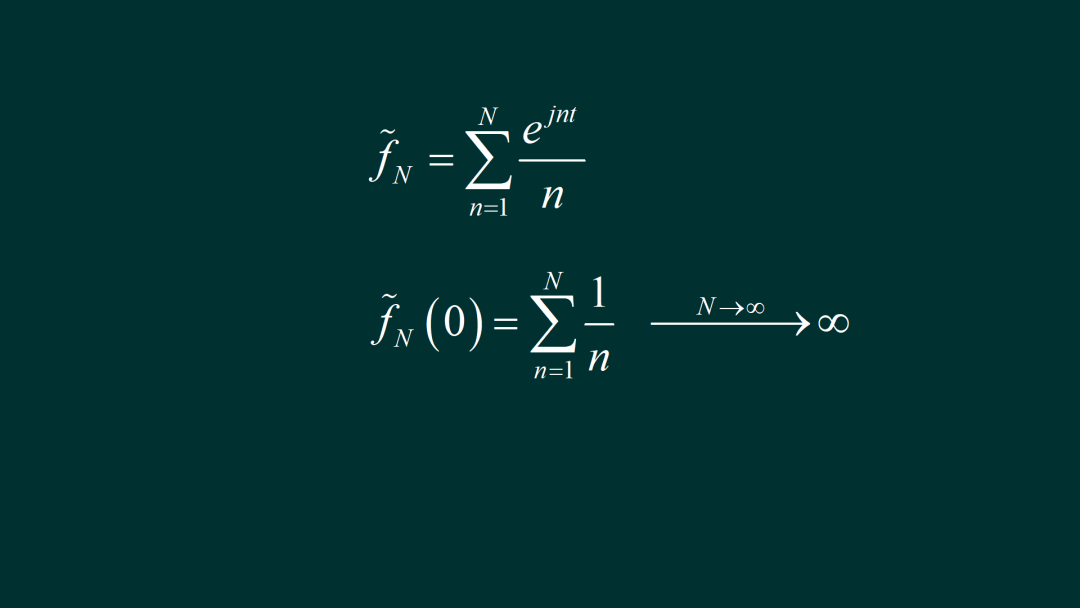
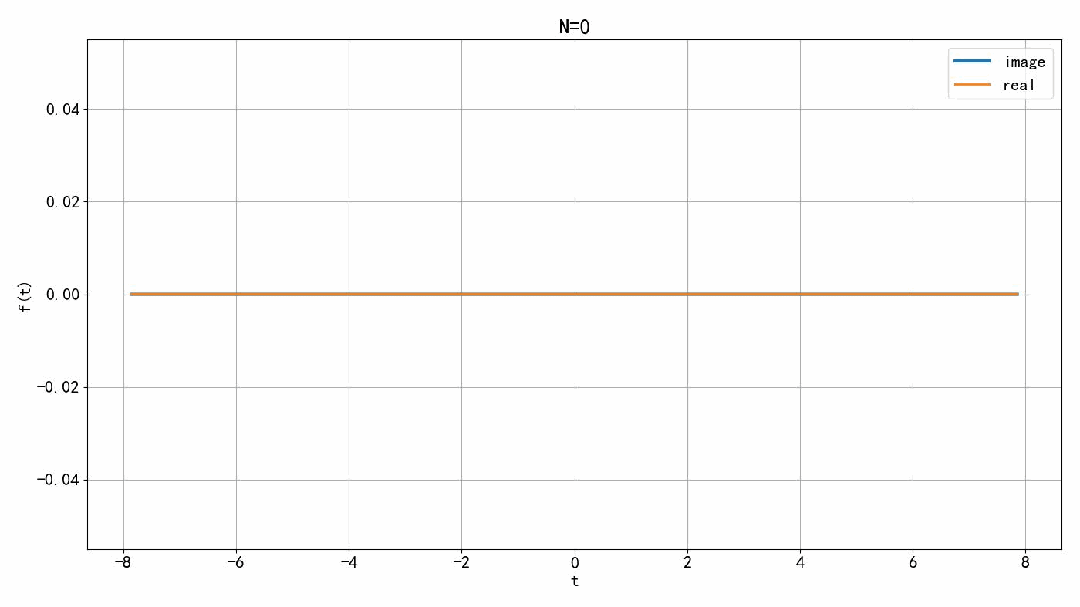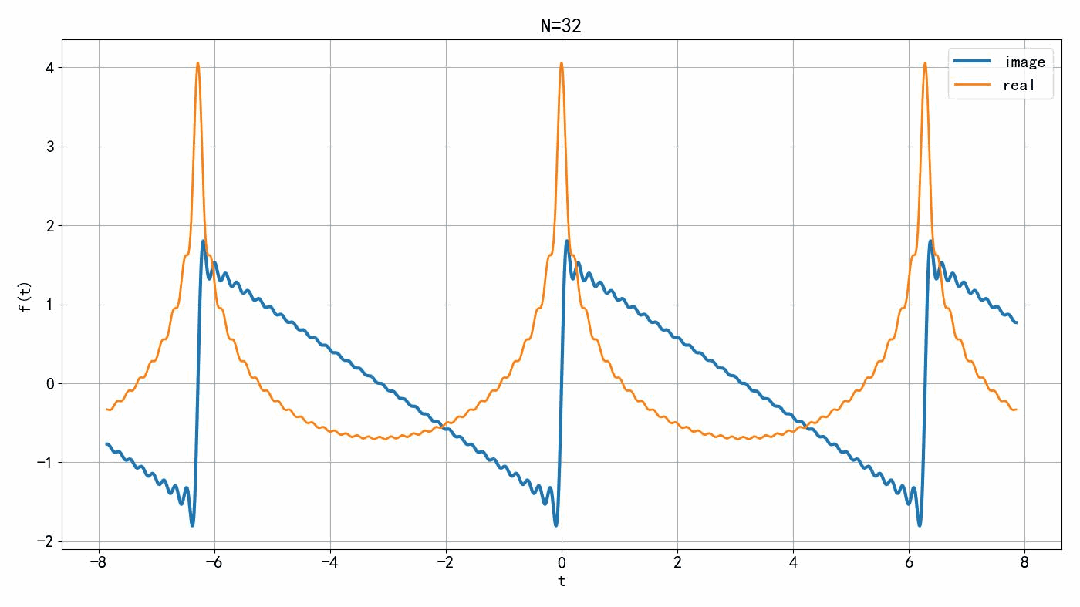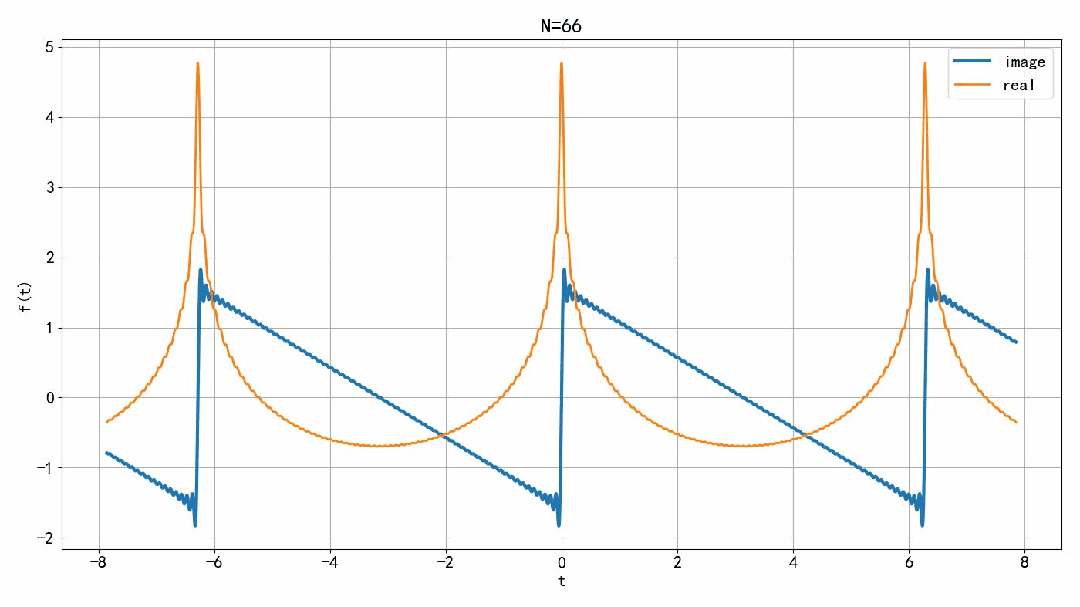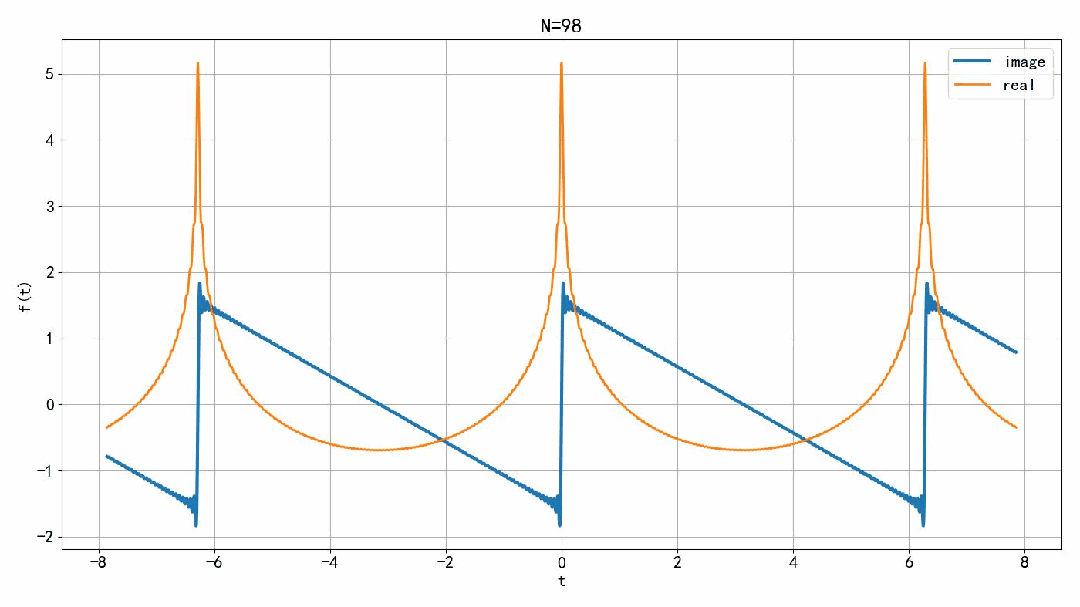
▲ 图1.2.2 右边傅里叶级数项叠加之后的实部和虚部本文讨论了锯齿波行的傅里叶级数有限项之和信号收敛的问题。 如果是对称的有限项叠加,在 t=0 处信号不会发散。但是如果只叠加半边的有限项,信号在 t=0 处会发散。这是信号分解中的对称破缺现象。