一元向量值函数,简单来说就是一个变量作为输入,输出结果是一个向量的函数。
这个叫什么来着,好像是向量场分析?

第一种的样子是这样的

第二种是参数方程和空间曲线
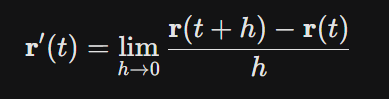
其导数也是很普遍的定义
一元向量值函数的导数也是一个向量值函数,表示曲线在某一点处的切向量。
雅克布矩阵只是名字唬人,你要理解它的内涵以后估计也不害怕了~我以前特别喜欢看机器人学,里面有着大量的雅克布矩阵,当时确实是看不懂,但是现在返回来再看就明白不少,机器人内部确实是有着大量的矩阵,各个关节在改变,所以这种矩阵的改变,我们怎么表示?雅克布矩阵就是干这个事情的,逆运动学解算也有的。
雅可比矩阵就像是一个“变化速率表”
雅可比矩阵就是用来描述这种“多因素共同影响”的数学工具。它可以告诉我们,当我们稍微改变输入的各个分量时,输出会发生怎样的变化。
雅可比矩阵是一个矩阵,它的元素是函数对各个变量的偏导数。
它描述了多元函数在某一点的局部线性变化。
你可以把它看作是一个“变化速率表”,告诉你在某个点上,改变输入的各个分量会对输出产生怎样的影响。
假设有一个函数f(x,y) = x^2 + y^2。它的雅可比矩阵为:

这个矩阵告诉我们,当x增加一个很小的量时,函数值会增加大约2x倍;当y增加一个很小的量时,函数值会增加大约2y倍。
Python实现所有算法-雅可比方法(Jacobian) ---很多时间以前写过,但是我都不记得了。
我们有一个弹簧,它的长度会随着施加的力而变化。如果我们同时从两个方向拉伸这个弹簧,弹簧的长度变化就会受到这两个方向力的共同影响。
有一个函数,它把两个数作为输入,输出一个数。这个函数就像一个机器,你给它两个数字,它就吐出一个结果。雅可比矩阵就是这个机器在某个特定输入点上的“说明书”,告诉你如果稍微调整一下输入的两个数字,输出会如何变化。
想象站在一座山坡上。你的位置可以用两个坐标(x, y)来表示,而你的高度就是函数的值。雅可比矩阵就像是一张地图,告诉你站在当前位置时,朝哪个方向走,坡度会变得更大或者更小。
在向量分析中,雅可比矩阵(Jacobian matrix)是函数的一阶偏导数以一定方式排列成的矩阵。它描述了多元函数在某一点的局部线性逼近。简单来说,雅可比矩阵可以看作是多元函数的导数的推广。
假设有一个从n维欧几里得空间映射到m维欧几里得空间的函数:
F: ℝⁿ → ℝᵐ这个函数可以表示为:
F(x₁, x₂, ..., xₙ) = (f₁(x₁, x₂, ..., xₙ), f₂(x₁, x₂, ..., xₙ), ..., fₘ(x₁, x₂, ..., xₙ))那么,函数F在点x处的雅可比矩阵J定义为:
J(x) =| ∂f₁/∂x₁ ∂f₁/∂x₂ ... ∂f₁/∂xₙ || ∂f₂/∂x₁ ∂f₂/∂x₂ ... ∂f₂/∂xₙ || ... ... ... || ∂fₘ/∂x₁ ∂fₘ/∂x₂ ... ∂fₘ/∂xₙ |
其中,每个元素J(i,j)表示函数fᵢ对变量xⱼ的偏导数。
线性逼近: 雅可比矩阵在某一点的值表示了函数在该点附近的最优线性逼近。
切平面: 对于一个从二维空间映射到三维空间的函数,雅可比矩阵在某一点的值表示了函数图像在该点处的切平面的法向量。
当雅可比矩阵为方阵时,它的行列式称为雅可比行列式。
上面就是单纯的科普,下面看在向量分析里面的三大计算:旋度、散度、梯度。它们分别从不同角度刻画了向量场的性质。

总结
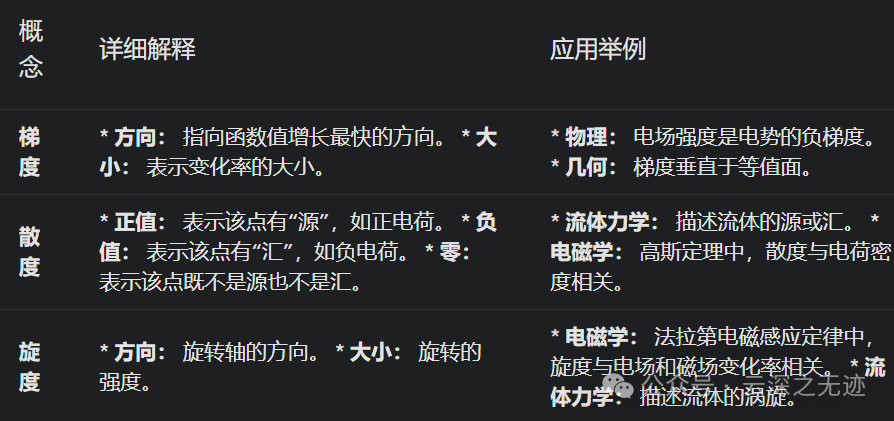
解释
梯度 将标量场转化为向量场,表示标量场在空间中的变化情况。标量场变化最快的方向。爬山,梯度指向山顶,即函数值增大的方向。
散度 将向量场转化为标量场,描述向量场在某点的发散程度。 水龙头,水流散开表示正散度,水流汇聚表示负散度。
旋度 将向量场转化为向量场,描述向量场在某点的旋转程度。 龙卷风,空气旋转的方向就是旋度的方向。
昨天看了会儿马同学,截图了好多,觉得帮助理解,我说的理解是忘不了的理解。
因为看的时候不停的截图可能有重复的。
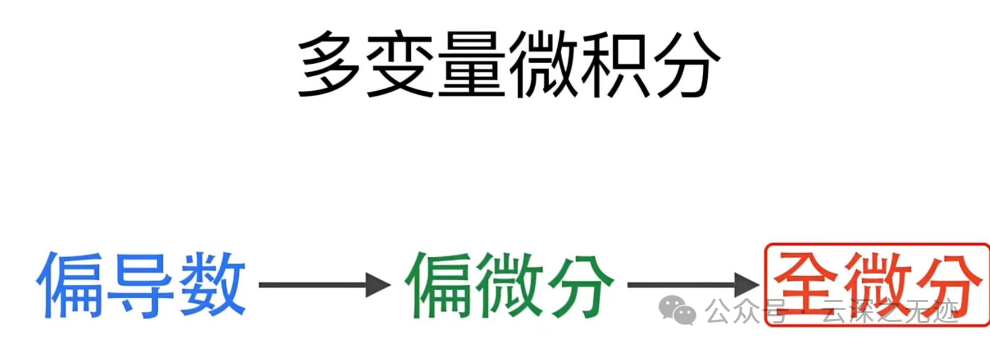
记住梯度是多变量微积分的世界里面的东西
偏微分 是多元函数对其中一个自变量求导数,而保持其他自变量不变。它反映了函数在某个特定方向上的变化率。
几何意义: 对于一个二元函数z=f(x,y),它的偏导数∂z/∂x表示在y固定时,函数z沿着x轴方向的变化率,也就是函数图像在x方向上的切线的斜率。
计算方法: 将其他变量视为常数,对目标变量进行求导。
例子:假设函数z=x^2+y^2,那么它的偏导数为:
∂z/∂x = 2x∂z/∂y = 2y
全微分 是多元函数在某点的一个线性近似,它反映了函数在该点附近所有方向上的微小变化。
几何意义: 对于一个二元函数z=f(x,y),它的全微分dz表示函数在点(x,y)处的切平面沿任意方向的增量。
计算公式:dz = (∂z/∂x)dx + (∂z/∂y)dy
可微的充分条件:一个多元函数在某点可微的充分条件是:该函数在该点的所有偏导数存在且连续。
几何意义:
可微意味着函数在该点附近可以用一个平面(切平面)来近似。
不可微意味着函数在该点附近的变化比较复杂,不能用一个简单的平面来近似。

就是这样的
偏微分 是对单个变量求导,反映函数在某个特定方向的变化率。
全微分 是对所有自变量求导,反映函数在任意方向上的变化率。
全微分 是由各个偏微分组成的。
假设有一个长方体,它的长、宽、高分别为x、y、z,体积V=xyz。
∂V/∂x = yz 表示在y和z固定时,体积V随长x的变化率。
∂V/∂y = xz 表示在x和z固定时,体积V随宽y的变化率。
∂V/∂z = xy 表示在x和y固定时,体积V随高z的变化率。
dV = yzdx + xzdy + xydz 表示体积V的微小变化量。
偏微分和全微分是描述多元函数变化的重要工具。
偏微分反映了函数在某个特定方向上的变化率。
全微分反映了函数在任意方向上的变化率。
全微分是偏微分的线性组合。
为什么需要全微分?
全微分可以用来求解隐函数的导数、求解极值问题、研究函数的局部性质等。
偏导数和方向导数有什么区别?
偏导数是方向导数的一种特殊情况,即沿坐标轴方向的方向导数。
全微分与可微性有什么关系?
函数在某点可微的充分条件是其在该点的所有偏导数存在且连续。
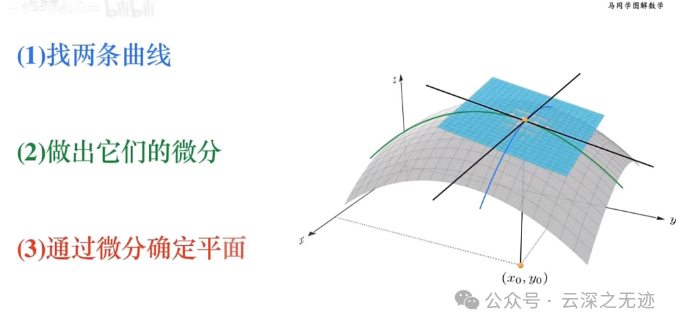
这个是偏微分的意思,两个偏导数可以构成一个切片面
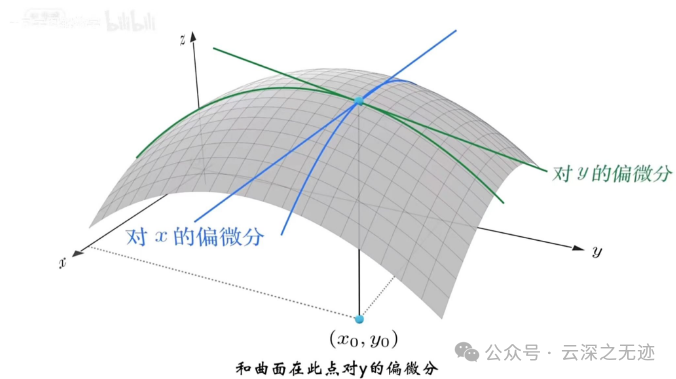
嗯,就是这样

偏导数的意思就是固定一个数来求另外一个数

这个是完整的定义

把这两个交线抬起来会构成一个平面
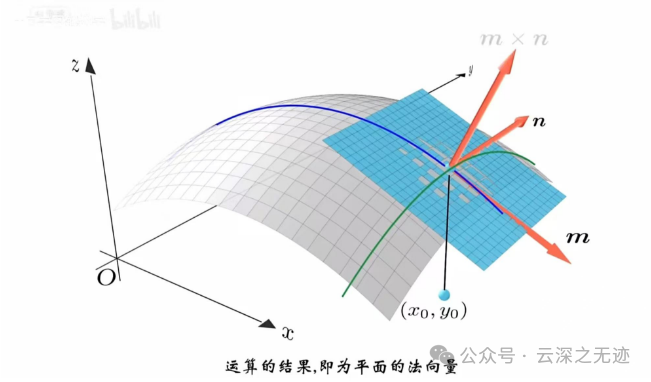
就是这样的

两个加起来就在在这点的偏导数

把他的一个面摆过来是可以看做一个单变量的导数
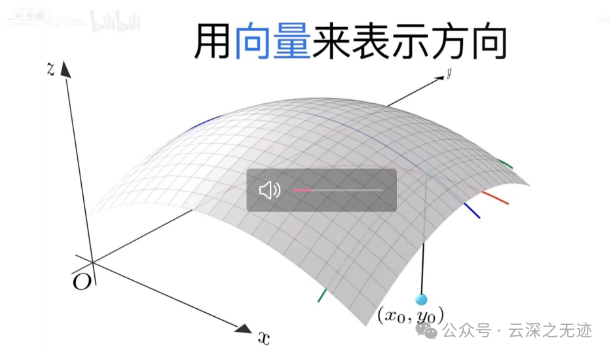
这里就开始引入方向导数的概念,先选定一个任意一个点就行
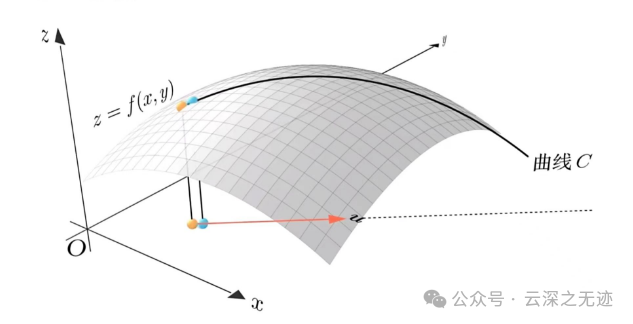
开始延伸
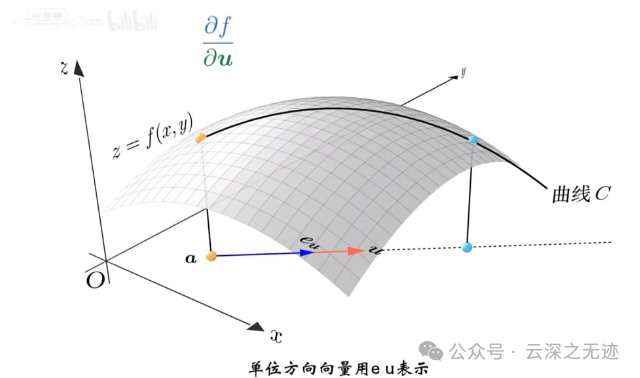
把它投影下来,这个向量就叫方向向量
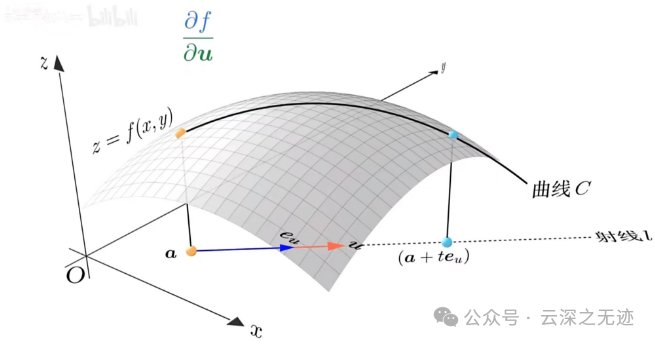
这里对这个方程重新写,点斜式,因为有一个定点和方向了
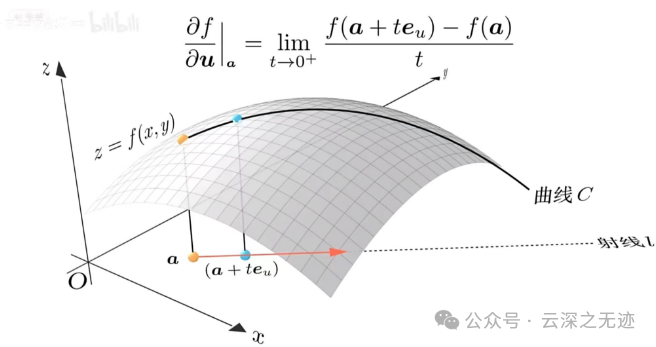
ok,当我们的t靠的很近的时候,就可以称为方向导数了

我们现在其实已经完成了从导数到方向导数的转变了,方向是沿着我们指向的方向。
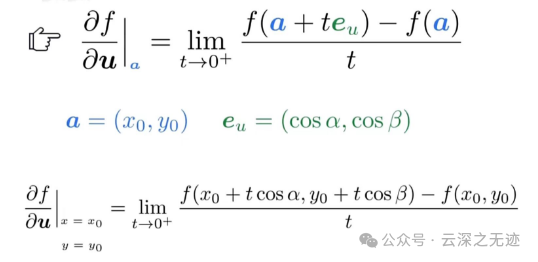
因为我们上面的公式有是有,但是还没有完全定义完成

这个就是我们常见的定义的样子了

继续定义,导数和微分相伴相生

可导就是和微分连接在一起的
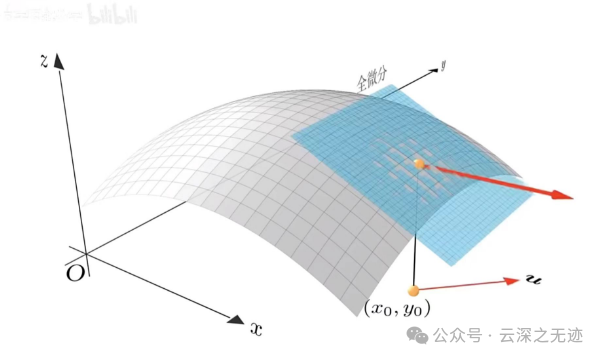
这个点处的全方向导数转一圈形成的一个面,叫全微分?
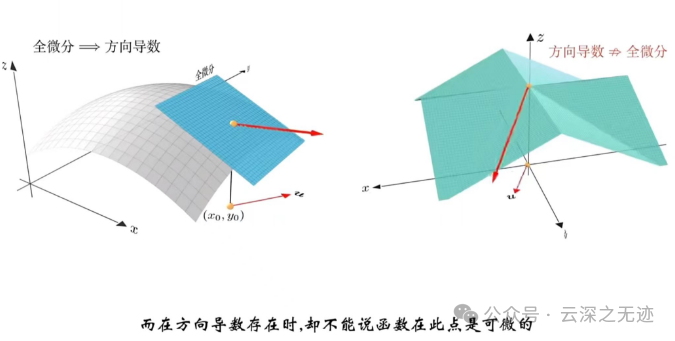
在一个很硬朗的面上面的时候,一个点的构成的方向导数簇不全在一个平面上,也就构不成全微分。
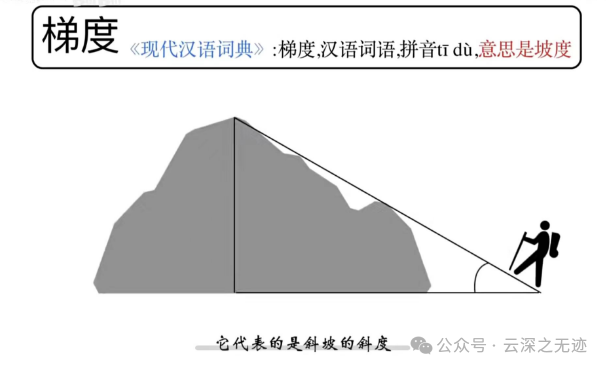
终于开始梯度了
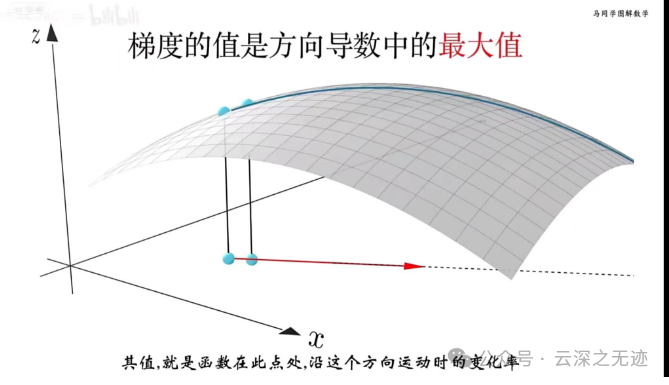
这里定义就自然而然的来了,这个值就是方向运动的变化率

我们可以先把线表示出来

这个图是非常漂亮的,投影是u,然后在这个点处重新画一个小坐标系,这个角度就出来了,就是上面公式里面的角度。

定义完了,开始找这个值到底是多少
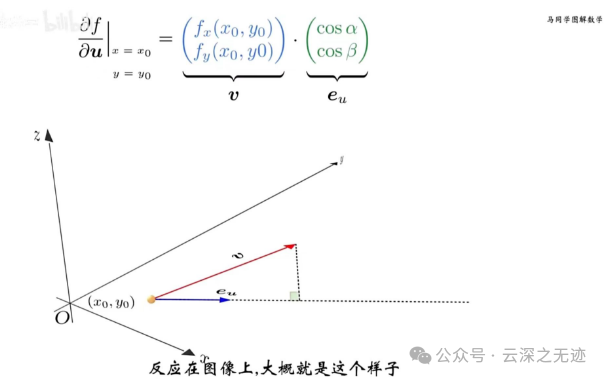
按照线性代数的理论,把它写成这样,一个点和一个方向向量
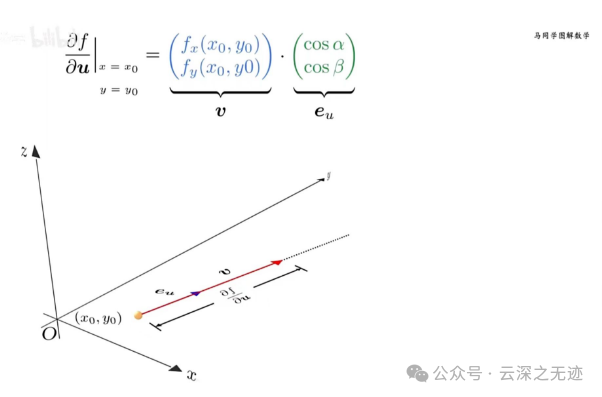
重合的时候就是最大的时候
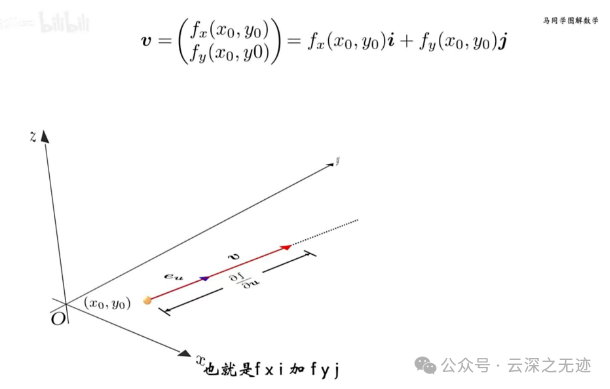
打开以后就有两个值

现在就计算出来了梯度

那不打算子
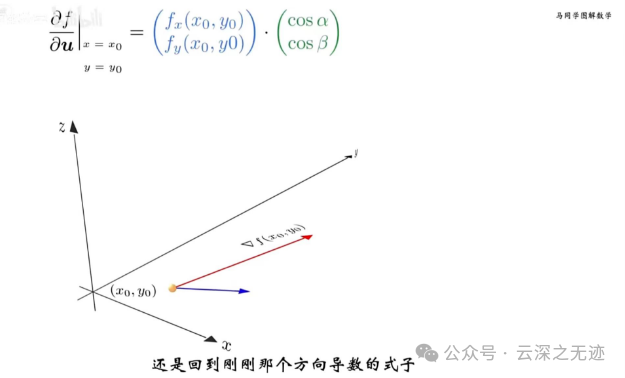
开始看这几个值的大小关系
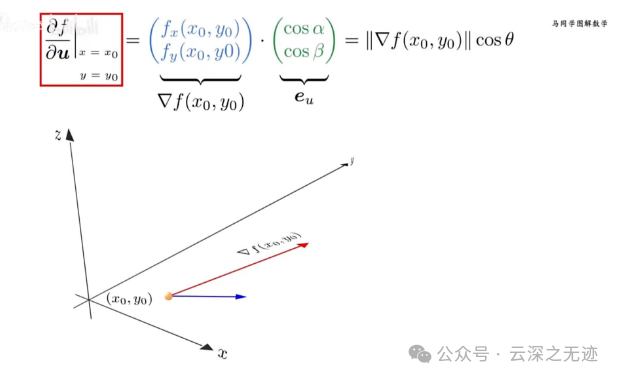

这段看书就好了
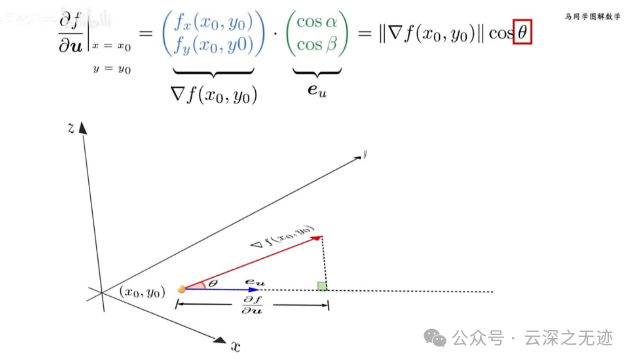
就是这个直角的虚线就是我们的值

可以在这个平面里面转圈,可以获得大小0

正交

劈叉
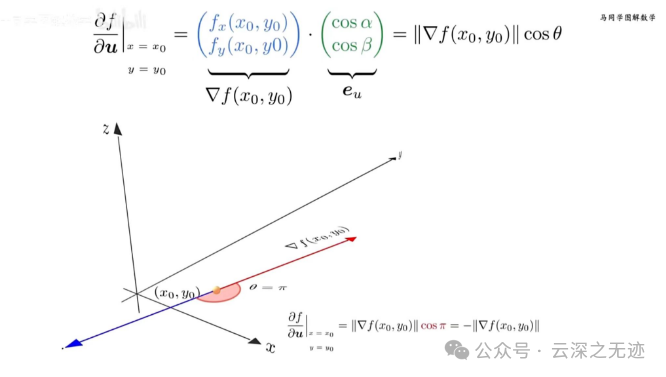
-的

最大的时候就是共线

把它翻过来就是最底部
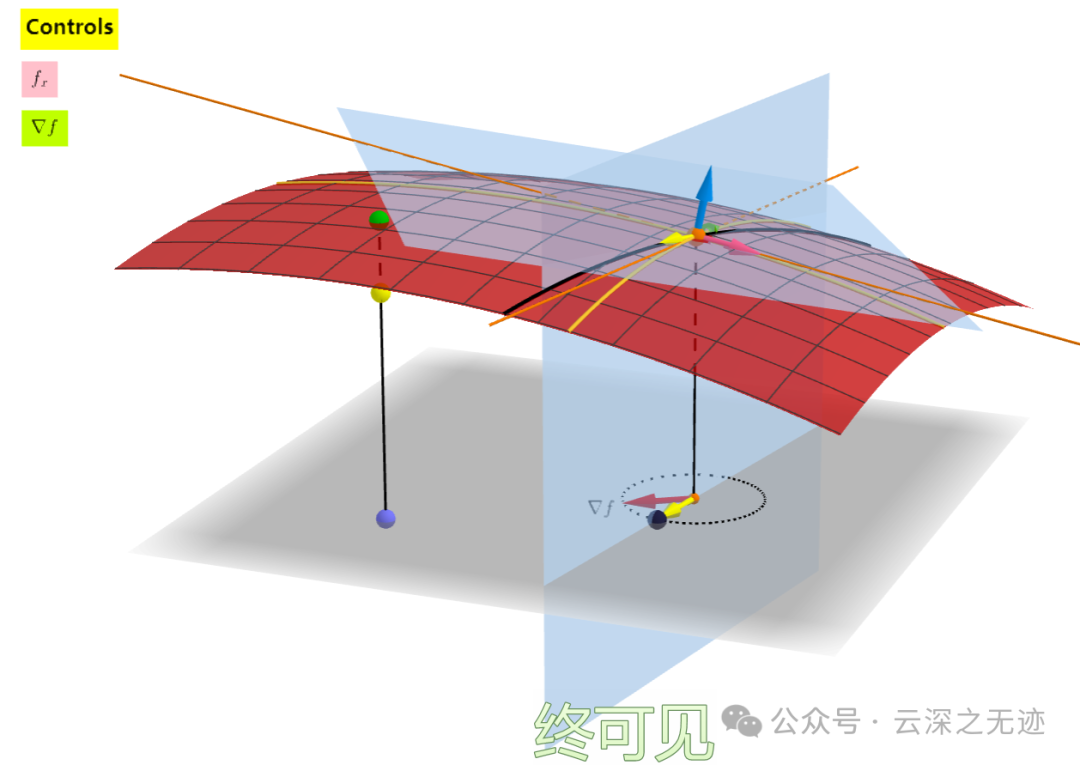
https://www.geogebra.org/m/YZQU6kdT概念: 梯度是一个向量,指向标量场增长最快的方向,其大小表示变化率的大小。
物理意义:
在物理学中,梯度表示一个标量场中某一点的“陡峭程度”,比如温度场中梯度最大的方向就是温度变化最快的方向。
电场强度就是电势的负梯度。
其中,f 是一个标量场,∇ 是向量微分算子。
grad f = ∇f = (∂f/∂x, ∂f/∂y, ∂f/∂z)概念: 散度是一个标量,描述了一个向量场在某一点的“发散程度”。如果散度为正,表示该点有源(如正电荷);如果散度为负,表示该点有汇(如负电荷);如果散度为零,表示该点既不是源也不是汇。
物理意义:
在流体力学中,散度表示流体的源或汇,正散度表示流体从该点发散出去,负散度表示流体向该点汇聚。
其中,F 是一个向量场。
div F = ∇ · F = (∂Fx/∂x + ∂Fy/∂y + ∂Fz/∂z)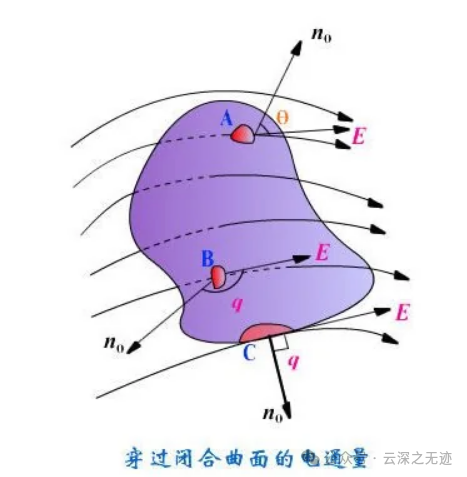
太抽象了
概念: 旋度是一个向量,描述了一个向量场在某一点的“旋转程度”。旋度的大小表示旋转的强度,旋度的方向表示旋转轴的方向。
物理意义:
在电磁学中,旋度表示磁场的涡旋性质。
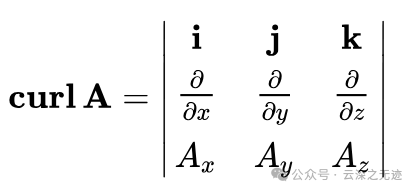
公式,矩阵形式
其中,F 是一个向量场。
curl F = ∇ × F = (∂Fz/∂y - ∂Fy/∂z, ∂Fx/∂z - ∂Fz/∂x, ∂Fy/∂x - ∂Fx/∂y)
推荐这本书
梯度: 山坡上的等高线,梯度指向坡度最陡的方向。
散度: 水龙头喷出的水,水流的速度和方向。
旋度: 龙卷风,空气旋转的方向和强度。
无所谓,继续写。
空间曲线是指在三维空间中的一条连续曲线。它可以用参数方程来表示:
r(t) = x(t)i + y(t)j + z(t)k其中,t 是参数,i、j、k 分别是 x、y、z 轴方向的单位向量。
定义: 在空间曲线上的某一点,与曲线在该点处的切向量方向一致的直线称为切线。
几何意义: 切线表示曲线在该点处的局部线性近似。
求法:
切向量: 曲线在 t 点处的切向量就是位置向量 r(t) 对参数 t 的导数:
r'(t) = x'(t)i + y'(t)j + z'(t)k切线方程: 设曲线在 t=t₀ 处的切点为 P₀(x₀, y₀, z₀),则过 P₀ 的切线方程为:
(x - x₀)/x'(t₀) = (y - y₀)/y'(t₀) = (z - z₀)/z'(t₀)非常的讽刺,全网都没有一个像样的图。
定义: 过空间曲线上一点的切线的所有垂直平面称为法平面。
几何意义: 法平面表示曲线在该点处的所有可能的方向。
求法: 法平面与切向量垂直,因此法平面的法向量就是切向量。
设法平面方程为 Ax + By + Cz + D = 0,则 A、B、C 就是切向量的坐标。
假设有一条空间曲线,其参数方程为:
r(t) = t²i + t³j + tk求当 t=1 时曲线的切线和法平面方程。
解:
求切向量:r'(t) = 2ti + 3t²j + k,当 t=1 时,r'(1) = 2i + 3j + k。
切点:当 t=1 时,P₀(1, 1, 1)。
切线方程:
(x - 1)/2 = (y - 1)/3 = (z - 1)/1法平面方程:2(x-1) + 3(y-1) + (z-1) = 0,即 2x + 3y + z - 6 = 0。
空间曲线的切线反映了曲线在某一点的局部方向。
法平面则表示了曲线在该点处的所有可能的方向。
曲率: 描述曲线弯曲程度的量。
挠率: 描述曲线偏离平面曲线的程度。
上面说的是空间里面的一条曲线,现在说一个完整的曲面。什么是曲面?
在三维空间中,曲面可以用一个方程 F(x, y, z) = 0 来表示。
球面:
x² + y² + z² - r² = 0定义: 过曲面上一点的所有切线的集合形成一个平面,这个平面称为曲面在该点的切平面。
几何意义: 切平面可以看作是曲面在该点处的局部线性近似。
曲面的切平面反映了曲面在某一点处的局部平面特性。
法线表示曲面在该点处的局部法线方向。
求解切平面和法线需要用到偏导数的概念。
切平面和法线在微分几何、物理学等领域有广泛的应用。

突然想起来自己以前还看过这个书,推荐

今天的封面