这个标题其实就是说明白了,矩阵可逆的意思,先别说我骚,看到后面就知道啦!

最近超爱的沙雕表情包
我觉得先给一个特别简单的定义可能更好:
矩阵: 食谱
伴随矩阵: 营养成分分析表
向量: 食材
线性变换: 做菜的过程
标题的意思就是,能不能回到我送你进矩阵之前的模样,要是还能回去那就是可逆,可逆其实讲的是“原料”。有没有那么一个矩阵,可以把变换过的原料再变回去。
(不能不说矩阵)一个矩阵就像是一个加工厂,它能把输入的原材料(向量)加工成输出产品(另一个向量)。这个加工过程可以看成是一个线性变换。
其实真正还原的过程是:伴随矩阵,登场了,
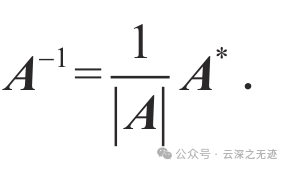
一个看起来很怪异的公式,一个矩阵的逆矩阵,可以通过计算它的伴随矩阵和行列式来实现。
对于一个n阶方阵A,它的伴随矩阵adj(A)的元素是A的代数余子式的代数伴随。也就是说,adj(A)的第i行第j列的元素是A的第j行第i列的余子式的(-1)^(i+j)倍。
adj(A)ij = (-1)^(i+j) * Mji其中,Mji是矩阵A去掉第i行第j列后得到的子式的行列式。
虽然伴随矩阵的计算过程比较复杂,但它在几何上也有着一定的意义。
在三维空间中,一个矩阵的伴随矩阵可以表示一个与原矩阵对应的平面的法向量。
可以看作是这个变换的“反向工程”配方。它告诉你,如果给你一个成品,如何通过逆向操作,分解出原来的原材料。
我学习主打一个字典学习法,我觉得理解每一个名词背后的意思,就是最深刻的学习过程。比如现在出现的线性变换,你能说出来吗?但是要明确一点,线性变换你要说明白现在在什么空间做变换。
在线性代数里面:线性变换可以看作是向量空间中的一个“拉伸”、“旋转”或者“扭曲”的过程,并且这些变换保持了原空间的直线和平行性。操作不会改变图形的本质(比如直线还是曲线),只会改变它的形状和位置。
但是我觉得,还是不够,继续深入这个话题。
矩阵与线性变换: 每一个线性变换都可以用一个矩阵来表示。矩阵的每一列代表了基向量经过线性变换后的像。
矩阵乘法与线性变换: 当我们用一个矩阵乘以一个向量时,实际上就是对
这个向量进行了线性变换。矩阵乘法观点-几何含义
我想说说第一个,矩阵和线性变换的关系:
基向量: 一个空间,比如二维平面。在这个平面上,我们可以选取一组基向量(比如x轴和y轴上的单位向量),它们可以表示空间中的任意一个向量。坐标轴就是基向量。
矩阵的列向量: 矩阵的每一列告诉我们,原来的基向量经过线性变换后变成了什么新的向量。也就是说,矩阵的每一列就是变换后的基向量。 也就是说矩阵的每一列告诉我们,原来的坐标轴(基向量)经过变换后变成了新的坐标轴。
其他点都是由基向量线性组合得到的,所以当基向量变化时,其他点也会跟着变化。
找到感觉了吗?本质来说,你要操作一个庞大的数据结构,里面装满了点,你可以想就是一个点集。然后这个线性变换就是你要施加的操作。首先我们在变换前建立一个坐标系,那么在这个坐标系里面的每一个点都能有一个独特的ID,也就是XY的坐标。然后去往新空间的时候怎么办?就是按照我们给的这个线性变化的规则。这个规则这里是用矩阵来描述的,一列就是一个小规则,描述的是基向量变换成了什么!!!注意,是基向量,其实没有对每一个点做变换。但是所有空间的点是以基向量作为局部参考系做位置上面的标定的。我们整理一下,我们现在有了要变换的点集,使用一个坐标系来给大家定位。接着给了一个矩阵,是一个方阵,每一列都说明了前面构造点集空间的基向量如何变化,起名字叫线性变换,接着整个变换过程要通过一个运算来完成,叫矩阵乘法。
有一个二维平面,基向量是i=(1,0)和j=(0,1)。现在有一个线性变换,它将i向量变为(2,1),将j向量变为(-1,3)。那么,这个线性变换对应的矩阵就是:
| 2 -1 || 1 3 |
回答为什么矩阵的列向量代表变换后的基向量?
矩阵乘法: 当我们用这个矩阵乘以一个向量时,实际上就是把这个向量分解到基向量上,然后分别对每个基向量进行变换,最后将变换后的结果相加。
坐标变换: 矩阵的每一列告诉我们,原来的坐标系中的一个单位向量在新的坐标系中的表示。
在变化过程中,我们不免的要研究,这个过程中,信息到底有没有损失。信号与系统里面还有无损传输呢。
就用矩阵的秩: 矩阵的秩表示了线性变换后空间的维度。如果秩小于原空间的维度,说明变换过程中丢失了一些信息,空间被压缩了。
如果这个函数满足以下两个条件,那么它就是一个线性变换:
加法性: 函数作用于两个向量的和,等于分别作用于这两个向量再相加。
齐次性: 函数作用于一个向量的倍数,等于将向量先乘以这个倍数,再作用于函数。把一个物体放大,这就是一个线性变换。无论你把物体放大多少倍,物体的形状不会改变,只是尺寸变大了。如果想把所有的点放大两倍,那么就需要一个缩放矩阵。这个矩阵会告诉纸上的每一个点,它们应该离原点远两倍。
旋转性(其实没有这个,但是我觉得加上完整):旋转门把人旋转一定角度,这也是一个线性变换。无论你进入旋转门的位置如何,你都会被旋转相同的角度。如果是顺时针旋转90度,那么就需要一个特定的旋转矩阵。这个矩阵会告诉每一个点,它们应该移动到新的位置。
晕了吗?其实这里才说到矩阵可逆,但是你要在这个概念之前了解更多。
可逆矩阵就好比一个可以完美复原的机器。也就是说,如果你把一个原材料放进去加工,得到一个产品。那么,存在另一个机器(逆矩阵),能把这个产品加工回去,还原成原来的原材料。 比如一个放大镜,它能把物体放大。如果有一个缩小镜(它的逆矩阵),就能把放大的图像缩小回原来的大小。
不可逆矩阵则像是一个单向的机器。你把原材料放进去加工后,得到的产物可能无法完全恢复原状。或者说,可能有多种不同的原材料能加工成同样的产品,导致无法确定原来的原材料是什么。 比如一个榨汁机,把水果榨成汁后,你无法把果汁还原成原来的水果。
正统定义看下面:
 我觉得可逆矩阵就是引入了1这个好算的东西
我觉得可逆矩阵就是引入了1这个好算的东西
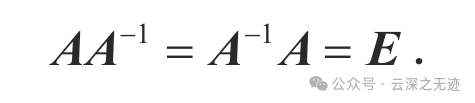
帅气
可逆矩阵,也称为非奇异矩阵,指的是一个方阵,且其行列式不为零。
换句话说,对于一个方阵 A,如果存在另一个方阵 B,使得 AB = BA = I(其中 I 是单位矩阵),那么矩阵 A 就是可逆的,矩阵 B 就是 A 的逆矩阵。
逆矩阵是对于一个可逆矩阵 A 而言的,它是一个满足 AB = BA = I 的矩阵 B。可以将逆矩阵看作是矩阵的“倒数”,在矩阵运算中起到类似于数的倒数的作用。
唯一性: 一个可逆矩阵的逆矩阵是唯一的。
行列式: 可逆矩阵的行列式不为零。
转置矩阵: 可逆矩阵的转置矩阵也是可逆的,且 (A')^(-1) = (A^(-1))'。
乘积: 若 A 和 B 都是可逆矩阵,则 AB 也是可逆的,且 (AB)^(-1) = B^(-1)A^(-1)(注意顺序)。
行列式法: 计算矩阵的行列式。若行列式不为零,则矩阵可逆。

事实上,行列式不为0其实是一个判断的充要条件
A的特征值λ≠0特征值是描述矩阵的一种重要性质,一个矩阵可逆当且仅当它的所有特征值都不为零。
ank(A) = n矩阵的秩等于其阶数,即矩阵的行向量或列向量线性无关。
Ax=0 只有零解x=0这意味着矩阵A的列向量线性无关。对于任意非零向量b,方程Ax=b总有唯一解这个条件与前句条件是等价的。
A = E1E2...Ek其中,Ei是初等矩阵。
矩阵的可逆性反映了矩阵所代表的线性变换的可逆性。如果一个线性变换是可逆的,那么它对应的矩阵就是可逆的。
初等变换法: 对矩阵进行初等变换,若能变换为单位矩阵,则原矩阵可逆。
秩法: 若矩阵的秩等于其阶数,则矩阵可逆。
伴随矩阵法: 利用伴随矩阵求逆矩阵。
初等变换法: 将增广矩阵 [A, I] 通过初等行变换化为 [I, A^(-1)] 的形式。
高斯消元法: 利用高斯消元法求解线性方程组。
线性方程组: 求解线性方程组 Ax = b 时,若 A 可逆,则解为 x = A^(-1)b。
线性变换: 可逆矩阵表示一个可逆的线性变换。

特征值不能缺席。