PPPPP级数-发散上天也可emo到尘埃里,先看这热热身。
然后就是两个老熟人,背口诀一样,绝对收敛就是加绝对值收敛。
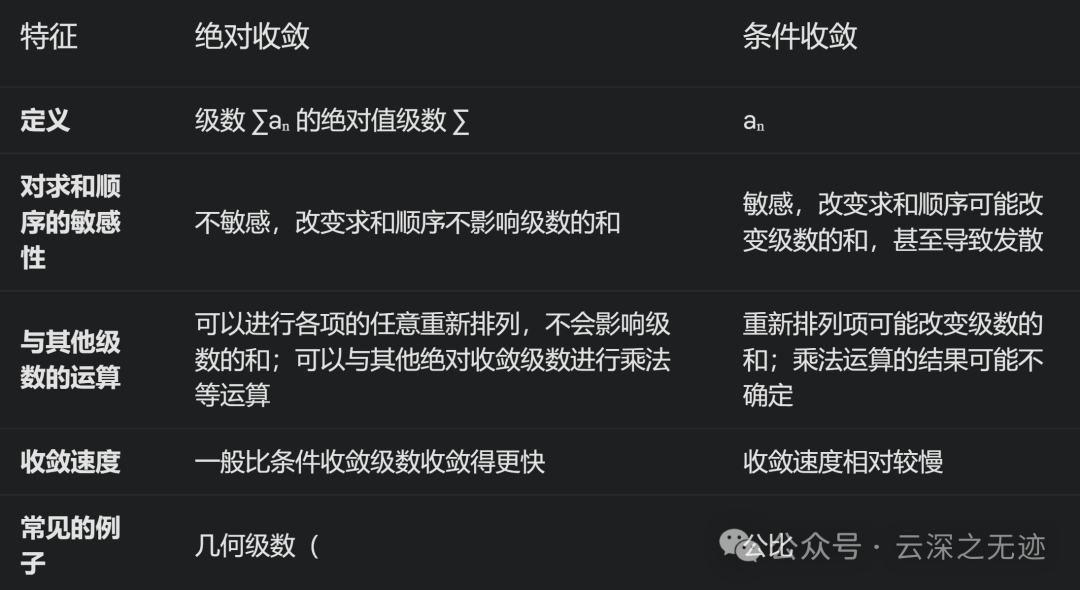
定义: 如果一个级数 ∑aₙ 的各项的绝对值构成的级数 ∑|aₙ| 收敛,那么称原级数 ∑aₙ 绝对收敛。
意义: 绝对收敛是一个更强的收敛性质。绝对收敛的级数具有更好的性质,例如,可以任意改变求和顺序而不影响级数的和。
绝对收敛蕴含收敛: 如果一个级数绝对收敛,那么它一定收敛。
定义: 如果一个级数 ∑aₙ 收敛,但其绝对值级数 ∑|aₙ| 发散,那么称原级数 ∑aₙ 条件收敛。
意义: 条件收敛的级数对求和顺序比较敏感。改变求和顺序可能会改变级数的和,甚至可能导致级数发散。
条件收敛的级数对求和顺序敏感: 改变求和顺序可能改变级数的和,甚至可能导致级数发散。
所以这两个是只适用于幂级数吗?绝对收敛和条件收敛的概念适用于所有无穷级数,而不仅仅是幂级数。

好的,知道了
幂级数:
∑(从n=1到∞) (-1)^(n+1) / n (交错调和级数)是条件收敛的。
∑(从n=0到∞) xⁿ/n! 是绝对收敛的(对于任意实数x)。
一般无穷级数:
∑(从n=1到∞) 1/n² 是绝对收敛的。
∑(从n=1到∞) (-1)^(n+1) / √n 是条件收敛的。
收敛半径
收敛半径是一个非负实数,它表示一个幂级数能够收敛的最大范围。简单来说,就是以幂级数的展开中心为圆心,收敛半径为半径的圆内(或区间),幂级数都能收敛。
将幂级数的收敛看作一个圆盘,收敛半径就是这个圆盘的半径。在圆盘内部,幂级数收敛;在圆盘外部,幂级数发散;而在圆周上,收敛性是不确定的,可能收敛也可能发散。
开区间: 在收敛半径内的所有点,幂级数都绝对收敛。
闭区间: 在收敛半径的端点处,幂级数的收敛性需要进一步讨论,可能收敛,也可能发散。阿贝尔定理可以帮助我们判断端点处的收敛性。
只有在收敛区间内,幂级数才能表示一个确定的函数。
比值判别法:
R = lim(n→∞) |a_n / a_(n+1)|根值判别法:
其中,R为收敛半径,a_n为幂级数的系数。
R = 1 / lim sup(n→∞) |a_n|^(1/n)
幂级数想象成一个弹簧:

当我们拉伸弹簧时,在一定范围内,弹簧的形变是可逆的,恢复原状后弹簧的性质不变。但是,如果拉伸过大,弹簧就会变形,甚至断裂。
幂级数也类似,当x取值在收敛半径内时,幂级数就像一个“柔顺”的弹簧,可以进行各种变形;但当x取值超出收敛半径时,幂级数就变得“僵硬”,无法表示原来的函数了。
收敛半径的存在是由于幂级数本质上是一个无限和,而无限和的收敛性与自变量的取值密切相关。简而言之,收敛半径就是幂级数的“有效范围”。
对幂级数逐项求导,一般情况下不会改变其收敛半径。
求导不改变高阶项的增长速度:当对幂级数逐项求导时,每一项的次数都会降低1,但并不会改变高次项相对于低次项的增长速度。
收敛半径由高次项决定:幂级数的收敛半径主要由高次项的系数决定,而求导并不会显著改变高次项系数的增长趋势。
接着说阿贝尔定理:

就是在一个范围里面,都是绝对收敛的。在这个边上,不确定,在外头可能是条件收敛也有困难是绝对收敛
∑(从n=0到∞) a_n * (x-x0)^n幂级数的样子,无穷级数
a_n 是常数系数
x 是变量
x0 是展开中心
1. 阿贝尔定理(收敛端点处):
如果幂级数在x=x0处收敛,那么它在开区间(x0-R, x0+R)上绝对收敛,其中R是幂级数的收敛半径。
此外,如果幂级数在x=x0+R处收敛,那么它在闭区间[x0, x0+R]上也收敛。类似地,如果幂级数在x=x0-R处收敛,那么它在闭区间[x0-R, x0]上也收敛。
2. 阿贝尔定理(发散端点处):
如果幂级数在x=x0处发散,那么对于所有满足|x-x0|>R的x,幂级数同样发散。
假如一堆数字,这些数字按照一定的规律排列成一串,就像一列火车一样。每个数字就像车厢,而整个火车就是所谓的“级数”。阿贝尔定理就是关于这列火车能不能顺利开到终点站(也就是收敛)的一个重要规则。
阿贝尔定理告诉我们:如果一列火车(级数)在某个地方(收敛点)停下来了,那么它在离这个地方不太远的地方(收敛圆的边界上),也可能停下来,但不一定能保证一定停下来。
假设有一列火车,它在离车站100米的地方停了下来。阿贝尔定理就告诉我们,这列火车在离车站99米、98米、甚至更近的地方,也可能停下来。但是,它不一定会在离车站101米或者更远的地方停下来.