信号系统中的几大变换都让我有点懵逼了,不墨迹了,干票大的,一把梭哈。
这写分析无一例外都是傅里叶分析家族的东西。首先就是为了分析频率成分,时域杂乱无章,频域一目了然。
频谱通常用图形表示,横轴表示频率,纵轴表示该频率成分的幅值。
幅度谱:表示不同频率成分的强度。
相位谱:表示不同频率成分的相位。
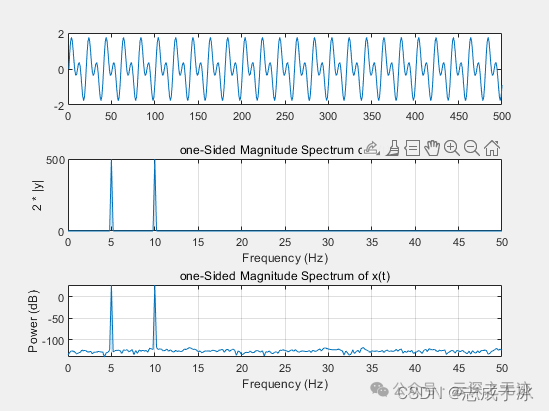
一个示意图
连续谱:非周期信号的频谱通常是连续的。
离散谱:周期信号的频谱是离散的,只有在谐波频率处有非零值。
功率谱密度:表示信号功率在不同频率上的分布。
又分为三种不同的谱类型。
谐波,就是频率是基波频率整数倍的波。
基波就是信号的基本频率,而谐波就是在这个基波基础上产生的倍频成分。

基波决定了信号的基本特征,而谐波则丰富了信号的细节,同时也可能带来一些负面影响。
这里面有两个概念是我平时混淆的,频谱分解和谐波分解。
定义: 将一个信号分解为不同频率的正弦波的叠加。
方法: 通常采用傅里叶变换。
目的: 分析信号的频率成分,了解信号的频谱特性。
定义: 将一个周期性信号分解为基波及其整数倍频率的谐波分量的叠加。
方法: 也是采用傅里叶变换,但更关注谐波成分。
目的: 分析周期性信号的谐波成分,了解信号的失真程度、非线性因素等。

平时用的多的是频谱分解
谐波分解是频谱分解的特例: 谐波分解可以看作是频谱分解在周期性信号上的一个特例,因为周期性信号的频谱是离散的,且只在基波频率及其整数倍频率处有非零值。
我想想还有什么内容没说。离散频率吧,这个重要。因为连续可以无限展开,但是离散的时候因为周期的问题就会变得不一样。另外在变换和级数里面用的特征函数也不一样。
复指数信号是线性时不变系统的特征函数,即如果输入是复指数信号,则输出也是复指数信号,只是幅度和相位可能发生变化。

事实上不管离散还是连续,都是正交的函数组,一个是级数,所以里面核心的是复指数函数,正余弦可以在整个频域展开。
复指数信号是一种数学形式,广泛应用于信号处理、通信系统等领域。其一般形式为:
x(t) = Ae^(st)A:振幅,表示信号的强度。
s:复频率,是一个复数,可以表示为s = σ + jω。
σ:实部,表示信号的衰减或增长速率。当σ>0时,信号随时间增长;当σ<0时,信号随时间衰减;当σ=0时,信号幅度不变。
jω:虚部,表示信号的旋转频率,ω是角频率。
欧拉公式将复指数信号与正弦信号和余弦信号联系起来:
e^(jωt) = cos(ωt) + jsin(ωt)上面就是傅里叶级数里面使用的分解量。
在离散的级数变换里面使用的是虚指数:
x(t) = Ae^(jωt)虚指数信号的幅度保持不变,仅有相位随时间变化。
A:振幅,表示信号的强度。
j:虚数单位,满足j² = -1。
ω:角频率,表示信号旋转的快慢。
t:时间。
旋转向量:虚指数信号看作是一个在复平面上旋转的向量。振幅A表示向量的长度,角频率ω表示向量旋转的角速度。随着时间的推移,这个向量在复平面上逆时针旋转。
正弦和余弦的组合:根据欧拉公式,虚指数信号可以展开为:
Ae^(jωt) = A(cos(ωt) + jsin(ωt))虚指数信号的实部表示一个余弦信号,虚部表示一个正弦信号。这两个正交的信号共同构成了一个旋转的向量。
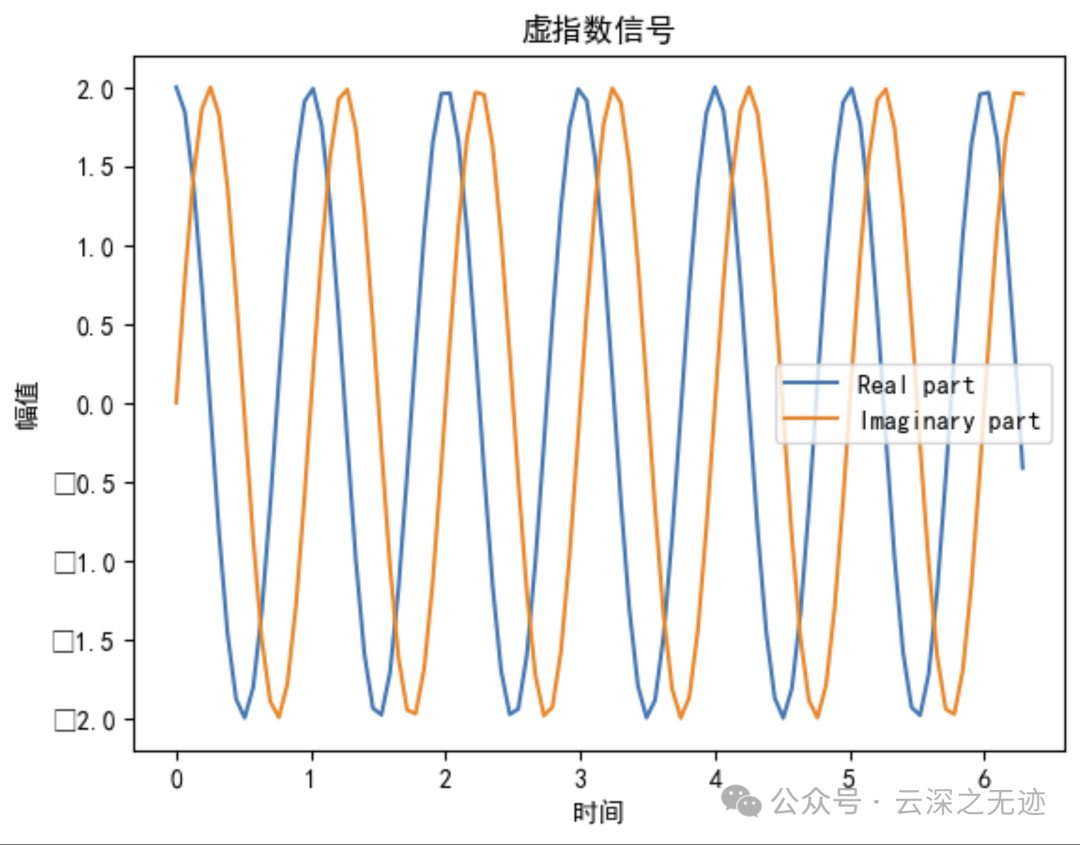
matplotlib的图不好看
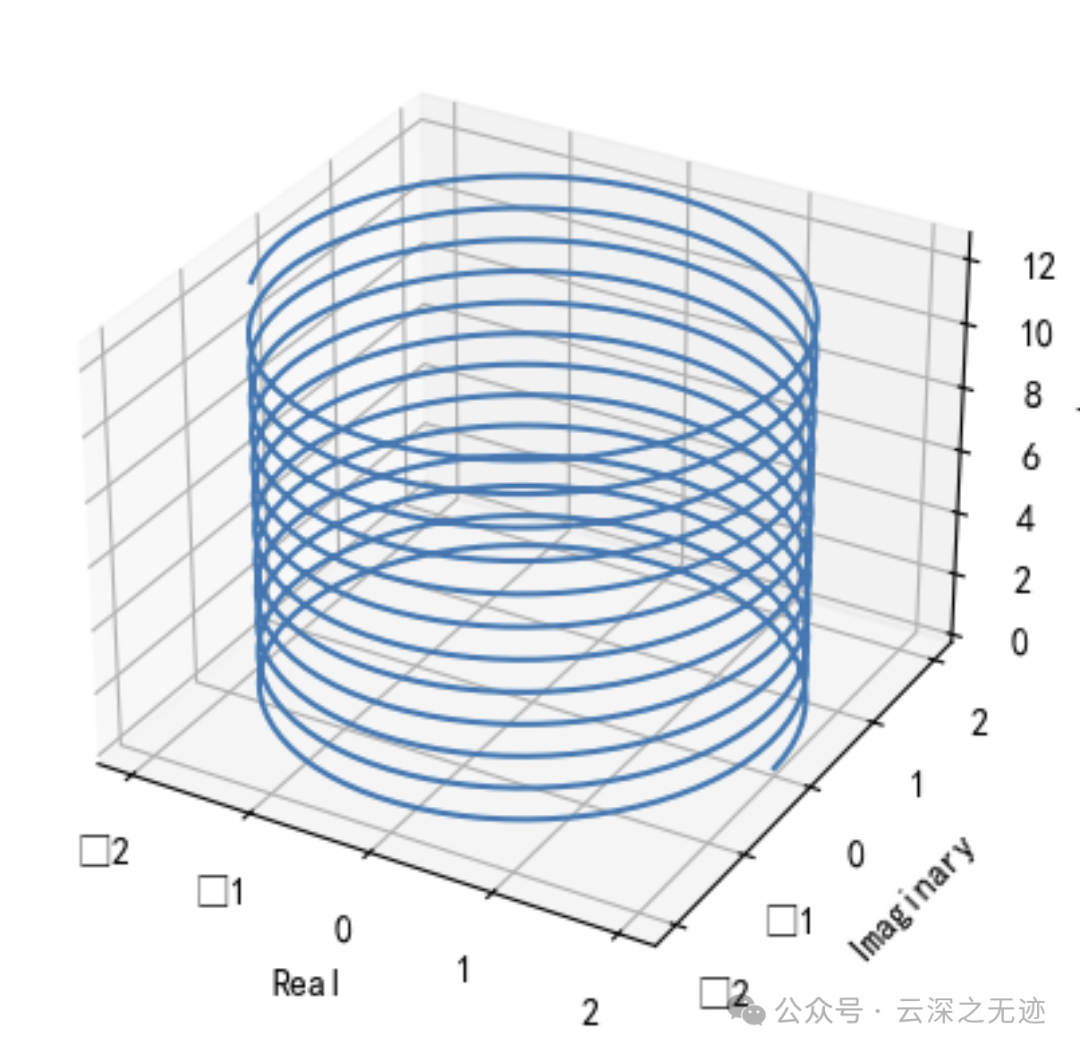
画了一个旋转的,这次🆗,可以从上往下看
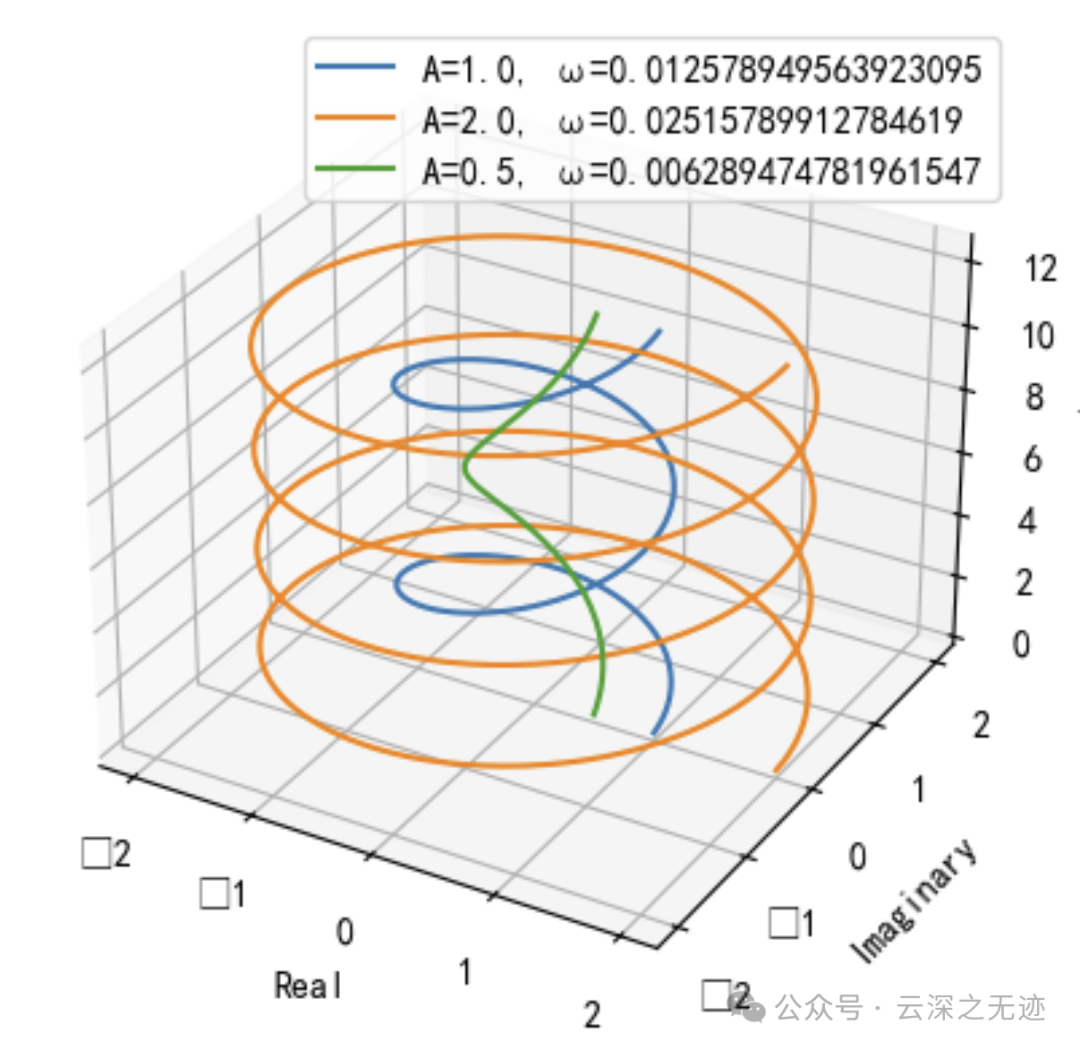
放浪形骸一点
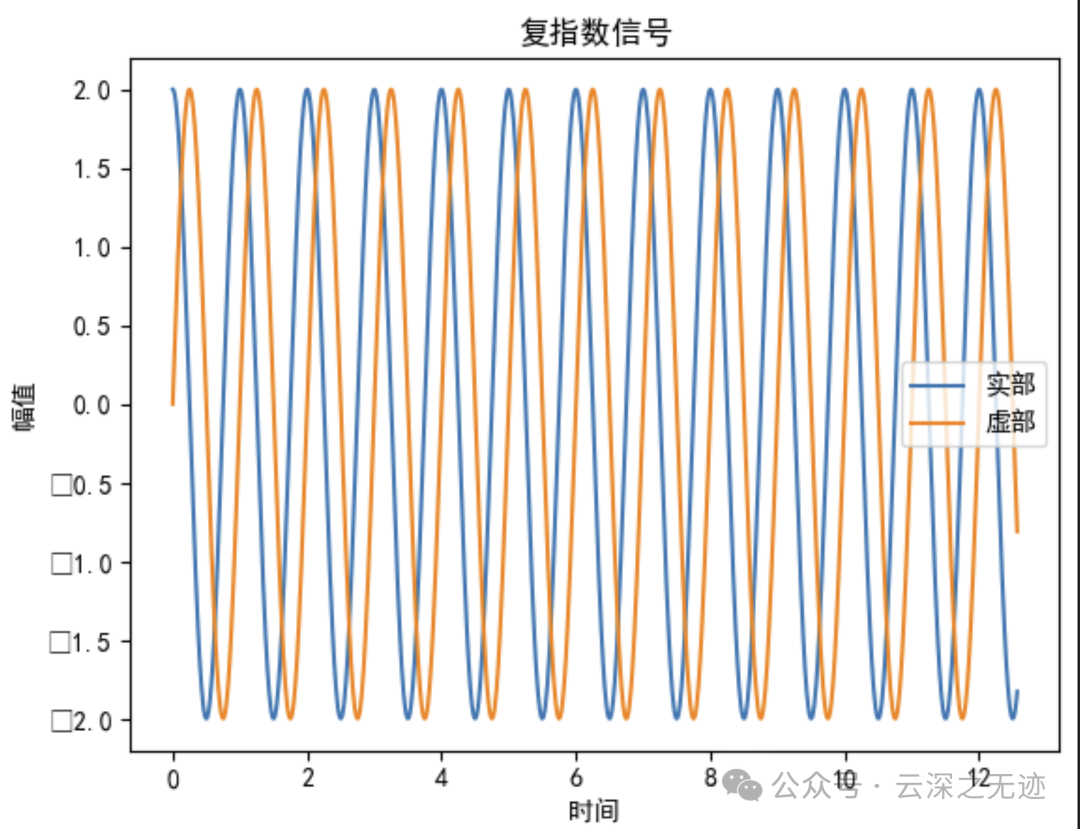
复指数信号也还是可以分解
这里放个照片当分隔符,哈哈哈。

好看捏
角频率:表示单位时间内相位变化的弧度数,通常用希腊字母ω表示,单位为rad/s。它与普通频率f的关系为:ω = 2πf。
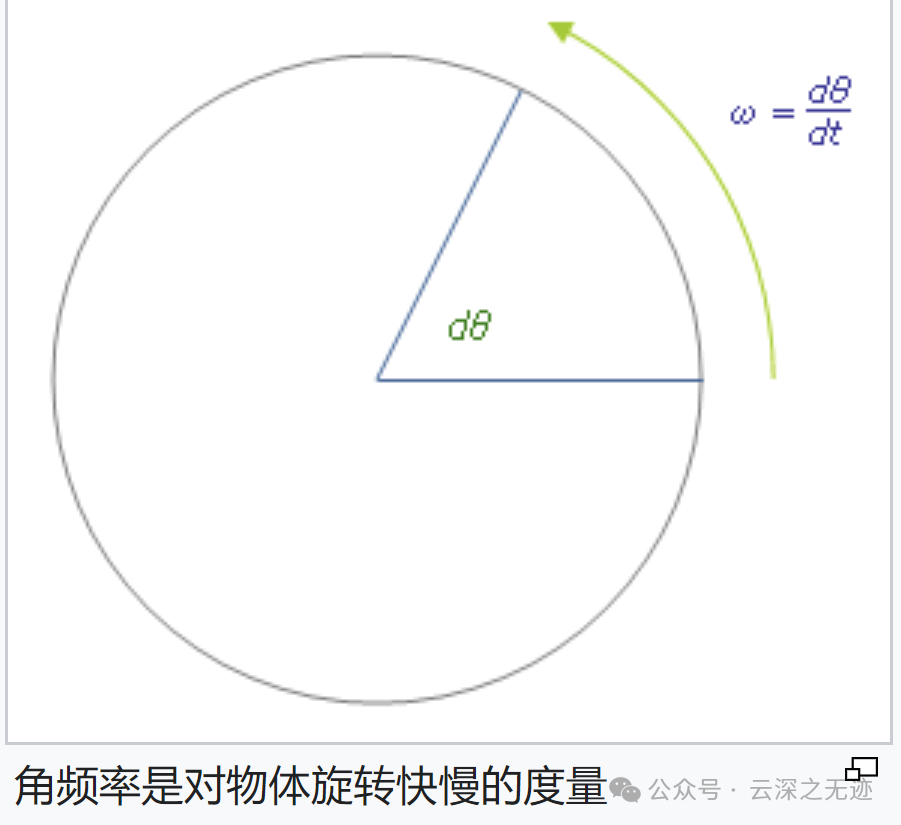
旋转,这个角度也叫相角

角频率在数值上是频率的2π倍
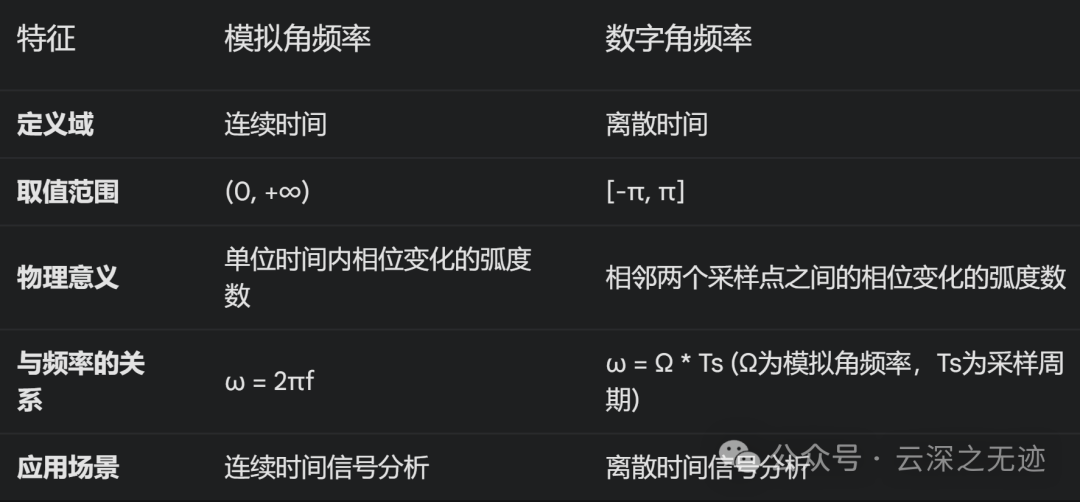
注意连续是无穷的,离散的是一圈,离散的是两个采样点之间的弧度
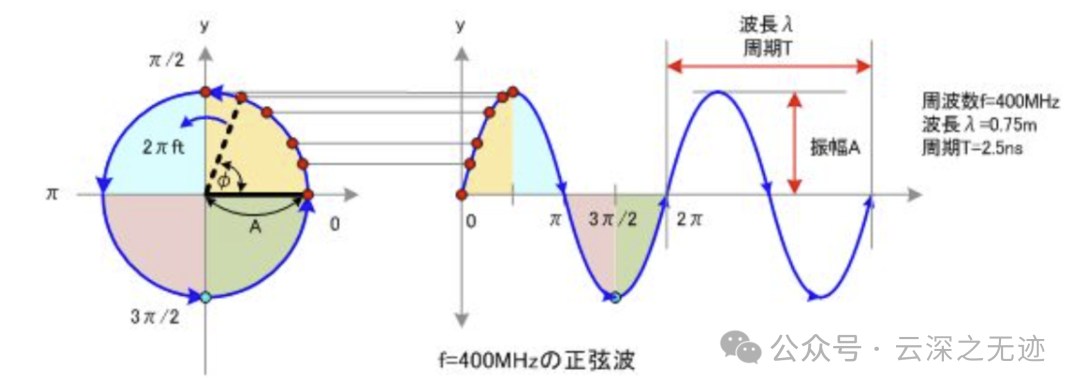
看左边的圆上的点之间的相角
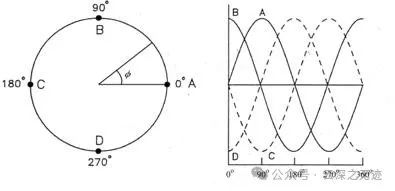
直观的理解,模拟角频率的概念是每秒多少弧度,数字角频率的概念是每个采样点之间多少弧度。
混叠就是,对不同频率的信号采样获得了相同的离散序列。
一个人在坐摩天轮,摩天轮以固定的频率转动。我们正对着摩天轮进行连续的拍照,拍摄之间隔着固定的时间,或者说是固定的频率(采样频率),可以得到一组相片。可以想象,如果变换摩天轮的频率,再拍照的话,是有可能获得同一组相片的,这就是混叠。
转的快了,拍的照片也快,但是现在一样了,那就是混叠啦。
数字角频率的概念是每个采样点之间多少弧度,又因为这是在单位圆上进行采样,自然可以知道两个采样点最大的间隔是
不难得出,数字角频率ω具有周期性,周期为2π.
一般取值范围为 :
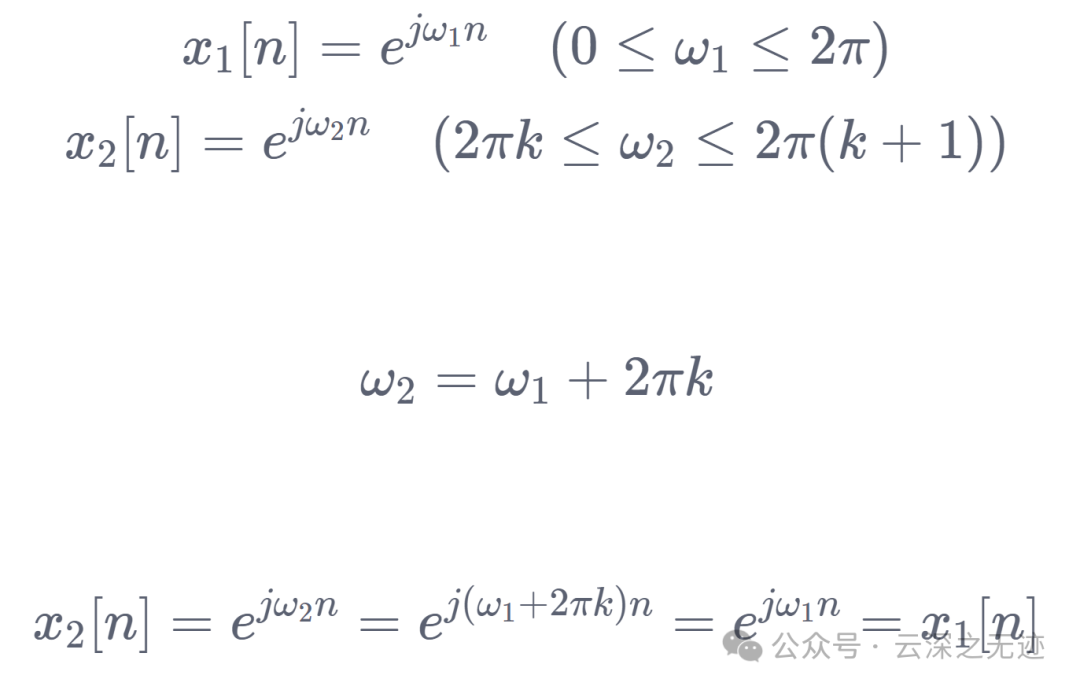
看这个例子,1和2就可以统一起来
离散频率是相对于连续频率而言的。在连续时间信号中,频率可以取任意实数值;而在离散时间信号中,频率的取值范围是有限的,且是离散的。
形象地说,连续频率就像一条连续的数轴,上面每个点都对应一个频率;而离散频率就像数轴上的一组离散的点,只有这些点对应的频率才有意义。
为什么有这个东西?
采样定理: 连续时间信号在数字化过程中,需要经过采样。采样频率的限制导致了离散时间信号的频谱是周期性的,且只有在某些特定的频率点上有值,这些点就是离散频率。
数字信号处理: 数字信号处理算法都是基于离散时间信号的,因此处理的频率也是离散的。
折叠频率: 由于采样定理,离散时间信号的频谱是周期性的。如果采样频率不够高,就会出现频谱混叠的现象,即高频成分的能量会“折叠”到低频部分,导致频谱失真。
奈奎斯特频率: 奈奎斯特频率是采样频率的一半,是能够无失真恢复原始信号的最高频率。
表示起来有两种:
数字角频率: 通常用数字角频率ω来表示离散频率,其范围是-π到π。
归一化频率: 将数字角频率除以π,得到归一化频率,范围是-1到1
实际物理频率表示物理信号的真实频率; fs为采样频率,表示ADC采集物理信号的频率,由奈奎斯特采样定理可以知道,fs必须≥信号最高频率的2倍才不会发生信号混叠,因此fs能采样到的信号最高频率为fs/2。
从工程上来讲,获得一个数字角频率,要先确定采样频率,因此,我们可以先把采样频率看成一个常量。
这时根据奈奎斯特采样定理,我们有一个最大不混叠模拟角频率分量,即采样频率的一半。对于发生混叠的,数值更高的模拟角频率分量,在采样频率确定的情况下,我们是无法分析出来的。最高频为π
算个题:
假设有一个模拟信号x(t) = cos(2π*100t),采样频率fs = 500Hz,则:
模拟角频率: Ω = 2π*100 = 200π rad/s
采样周期: Ts = 1/fs = 0.002s
数字角频率: ω = Ω * Ts = 200π * 0.002 = 0.4π rad
看看之间的联系
模拟角频率(Ω):描述连续时间信号在单位时间内相位变化的快慢,单位是rad/s。
采样周期(Ts):连续时间信号转换为离散时间信号时,相邻两个采样点的时间间隔。
数字角频率(ω):描述离散时间信号在相邻两个采样点之间的相位变化,单位是rad。
ω = Ω * Tsω:数字角频率
Ω:模拟角频率
Ts:采样周期
采样过程:将连续时间信号转换为离散时间信号时,相当于对信号进行抽样。采样周期越短,得到的离散时间信号就越能反映原始信号的细节。
频谱映射:采样过程会引起频谱的周期延拓。数字角频率的范围是[-π, π],而模拟角频率的范围是无限的。采样过程将模拟角频率映射到数字角频率的范围内。
这里出现名词啦!!!看看怎么个事情?
核心原因: 采样是将连续时间信号离散化的过程。这个离散化操作在频域上引入了一种周期性。
形象解释: 想象一下,我们用一个筛子筛沙子。筛子上的孔代表采样点,沙子代表连续信号。只有穿过筛子孔的沙子才能被收集到。这个过程就相当于对连续信号进行采样。
筛子孔的间隔:对应着采样周期。
筛过的沙子:对应着离散时间信号。
由于筛子孔是周期性分布的,所以筛过的沙子也会呈现出周期性的分布。同样,采样过程也给信号引入了周期性。
这句话是关键,因为孔是周期性分布的,所以这个沙子也是周期性的。
连续时间傅里叶变换(CTFT):连续时间信号的频谱是连续的,且可以取任意值。
离散时间傅里叶变换(DTFT):离散时间信号的频谱是周期性的,周期为2π。
为什么DTFT是周期性的?
采样公式: 离散时间信号x[n]可以表示为连续时间信号x(t)在采样时刻t=nT的取值,即x[n] = x(nT),其中T是采样周期。
DTFT的定义: DTFT的定义是将离散时间信号变换到频域,其表达式为:
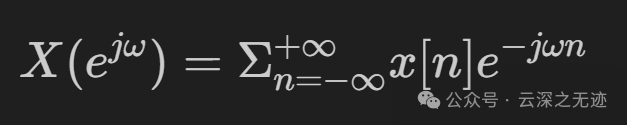

模拟角频率Ω:表示连续时间信号的频率,取值范围是(-∞, +∞)。
数字角频率ω:表示离散时间信号的频率,取值范围是[-π, π]。
采样过程将模拟角频率Ω映射到数字角频率ω的范围内。这个映射过程并不是一一对应的,而是多对一的。多个不同的模拟频率可能会映射到同一个数字频率上。
频谱混叠:当采样频率不满足奈奎斯特采样定理时,不同频率的模拟信号可能会混叠在一起,导致无法恢复原始信号。
采样过程是将连续时间信号转换为离散时间信号的过程。
采样过程会在频域上引入周期性,导致频谱周期延拓。
数字角频率的范围是[-π, π],而模拟角频率的范围是无限的。
采样过程将模拟角频率映射到数字角频率的范围内。
角频率Ω是物理频率的2π倍, 这个也称模拟频率。归一化频率是将物理频率按fs归一化之后的结果,最高的信号频率为fs/2对应归一化频率0.5,这也就是为什么在matlab的fdtool工具中归一化频率为什么最大只到0.5的原因。
归一化频率中不含fs的信息.圆周频率是归一化频率的2π倍,这个也称数字频率ω。
数字角频率是用来描述离散时间信号频率的一个量。它与模拟信号中的角频率类似,但由于离散时间信号的特殊性,数字角频率有一些独特的特点。
想象一个时钟,秒针每秒转一圈。在模拟世界中,我们用角速度来描述秒针转动的快慢。而在数字世界中,我们把时钟的秒针看成是一系列离散的点,每隔一段时间采样一次。这时,我们就用数字角频率来描述这些离散点之间的相位变化。

分割线
按照工具来看就是级数和变换。
级数对付周期信号,即使它是离散的。变换会范围大,包含了非周期信号(当然也是使用了周期延拓到非正常的周期中进行推导)。

可以这样的统一起来
傅里叶级数 主要用于分析周期信号,将信号分解为谐波分量。
傅里叶变换 则可以用于分析周期信号和非周期信号,将信号变换到频域。
离散时间傅里叶变换 是傅里叶变换在离散时间信号上的应用。
周期信号的傅里叶变换 和 周期序列的傅里叶变换 可以看作是傅里叶级数的另一种表示方式。
连续时间周期信号的傅里叶级数,离散时间周期信号的傅里叶级数:是连续时间周期信号的特殊情况,将周期信号分解为谐波分量的线性组合。
连续时间非周期的傅里叶变换:适用于连续时间信号,无论是周期性还是非周期性。
周期信号的傅里叶变换,周期序列的傅里叶变换:适用于离散时间信号,无论是周期性还是非周期性。
离散时间的傅里叶变换:是DTFT的离散形式,用于计算有限长离散时间信号的频谱。
也就是这7大分析,都称为频域分析。

周期信号的频谱是离散的,且只在谐波频率处有非零值。
非周期信号的频谱是连续的,可以表示信号在任意频率处的成分。
离散时间信号的频谱是周期的。
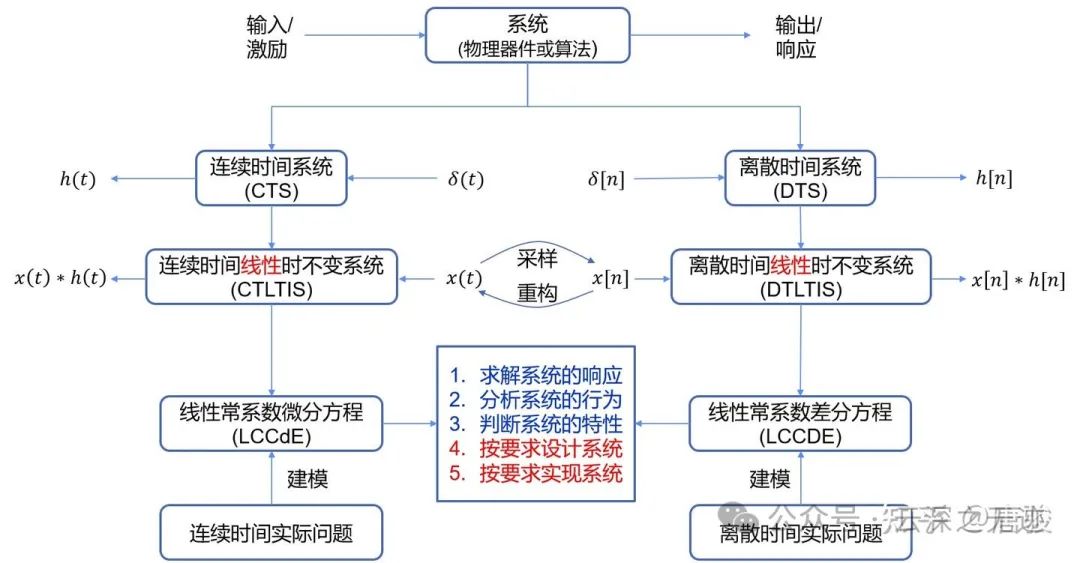
最后再反过来看,已经差不多走完了。
周期信号的傅里叶变换是什么样的?
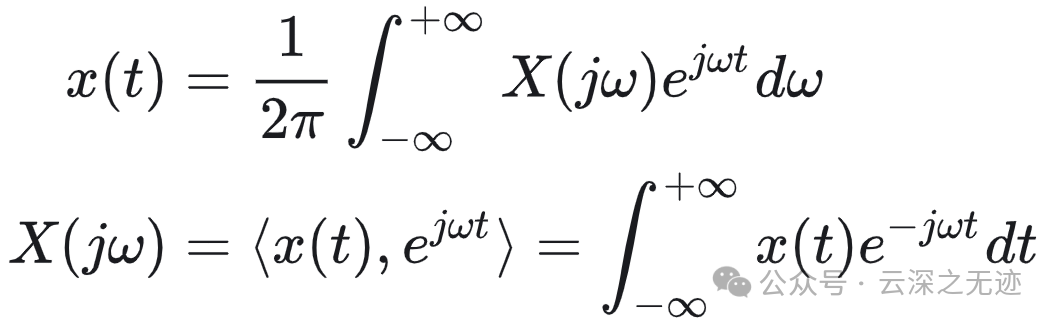
连续时间的傅里叶变换对
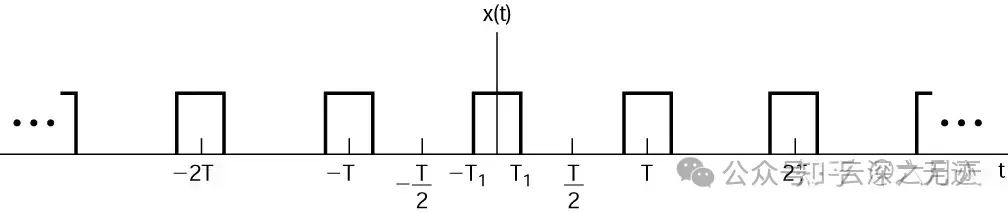
典型信号,周期方波

周期信号的傅里叶变换是其傅里叶级数系数在对应频率处的一系列冲激函数。
周期信号的频谱特性: 周期信号的频谱是离散的,只有在谐波频率处有能量。
冲激函数的性质: 冲激函数在频率域表示无限窄的频带,正好对应了周期信号的谐波分量。