秩(rank)是一个非常重要的概念,它反映了一个矩阵或向量组所包含信息的丰富程度。秩越大,说明线性无关性越强,包含的信息量就越大。
课本上面有两种秩,一种叫向量组(也叫n维向量),一个叫矩阵。
矩阵的秩:矩阵A的秩,记作rank(A),等于A的线性无关的行(或列)的极大数目。可以看作是矩阵中包含的本质信息的多少。如果一个矩阵的秩很高,说明它的行向量或列向量之间线性无关性强,包含的信息量就大;反之,如果秩很低,说明行向量或列向量之间存在较强的线性相关性,包含的信息量就少。从矩阵的角度出发,关注的是矩阵的行或列之间的线性关系。矩阵就像是一个表格,秩表示这个表格中有多少行或列的信息是真正有用的,不会被其他行或列的信息所重复。
向量组的秩:向量组的秩等于向量组中线性无关向量的极大数目。可以看作是向量组中线性无关向量的最大个数。秩越高,说明向量组包含的信息越丰富,越能张成一个高维的空间。从向量的角度出发,关注的是向量之间的线性关系。向量组就像是一群人,秩表示这群人中能独立思考的人数最多是多少。
线性无关才是重要的,彼此不能互相表示。
极大无关组才是秩的本真定义法。
线性无关: 这个部分组中的所有向量都是线性无关的。
极大性: 如果在这个部分组中添加任意一个原向量组中的向量,新的向量组就会变得线性相关。
那么,这个部分组就称为原向量组的一个极大无关组。
极大无关组就像是一个向量组中的“核心”,它包含了这个向量组中最多的线性无关的信息。任何想再添加进来的向量,都会与已有的向量产生线性关系,也就是可以被已有的向量表示出来。
确定向量组的线性相关性: 如果一个向量组的秩小于向量组中向量的个数,说明向量组线性相关。
这里其实还挺直观的,比如现在四个向量,秩为2,那就说明里面的两行向量可以被表示,你看,这不就是相关了。如果是秩=向量个数,不就是大家都线性无关。
如果秩等于向量个数,说明每个向量都提供了独立的信息,它们之间没有线性关系,即线性无关。
但如果秩小于向量个数,说明存在一些向量可以由其他向量线性表示,即它们之间存在线性关系,因此向量组线性相关。
向量空间的基: 极大无关组是向量空间的一组基。
线性变换的核与像: 极大无关组可以用来求线性变换的核与像的基。
矩阵的秩: 矩阵的秩等于其行向量组或列向量组的秩。
求极大无关组最常用的方法是通过初等行变换将向量组对应的矩阵化为行阶梯形矩阵或简化行阶梯形矩阵。
非零行的个数就是向量组的秩,而这些非零行对应的原向量就构成一个极大无关组。
一开始就是解方程的,所以有系数矩阵和增广矩阵的秩与线性方程组解的关系:
先说屁话哈,我们解了这么多年的方程,不能停留在几个未知数就要几个方程的地步了。
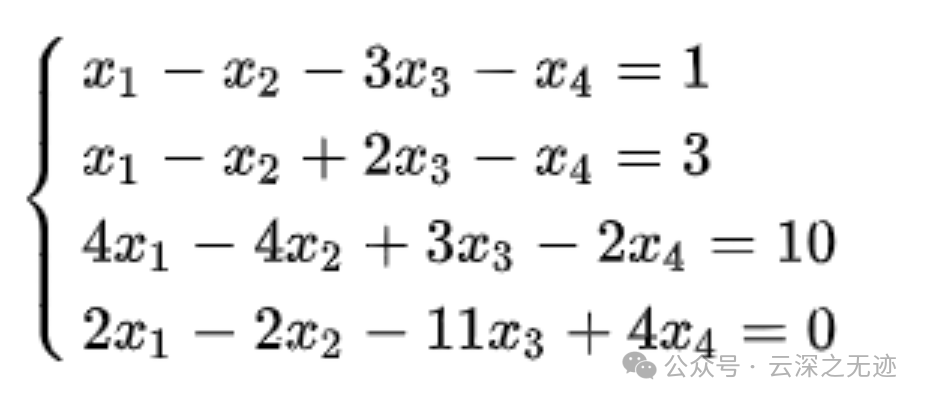
系数矩阵A:表示线性方程组中未知数系数所构成的矩阵。
增广矩阵[A b]:将系数矩阵A与常数项向量b合并得到的矩阵。
增广矩阵的秩等于系数矩阵的秩:即rank([A b]) = rank(A)。
解释: 这意味着增广矩阵中没有引入新的线性无关方程,即常数项b可以由系数矩阵的列向量线性表示。换句话说,方程组是相容的,有解。
这个要主要,等于是重要的标志,没有引入新的信息。
唯一解:当且仅当rank(A) = rank([A b]) = n(n为未知数的个数)时,方程组有唯一解。这个也好理解,就是我上面说的,每一个都线性无关,信息最大。
解释: 这意味着系数矩阵的列向量线性无关,且方程组的个数等于未知数的个数,方程组有且仅有一个解。
无穷多解:当rank(A) = rank([A b]) < n时,方程组有无穷多解。
解释: 这意味着系数矩阵的列向量线性相关,方程组的个数少于未知数的个数,自由变量的个数为n - rank(A),因此有无穷多组解。自由变量的名字很好听啊。这些变量没有约束,就是想写多少都可以。你想现在有4个方程,然后就求出来秩为1,意味着要有3个自由变量,自由就是无限。
无解:当rank(A) ≠ rank([A b])时,方程组无解。
解释: 这意味着增广矩阵中引入了一个新的线性无关方程,即常数项b不能由系数矩阵的列向量线性表示。
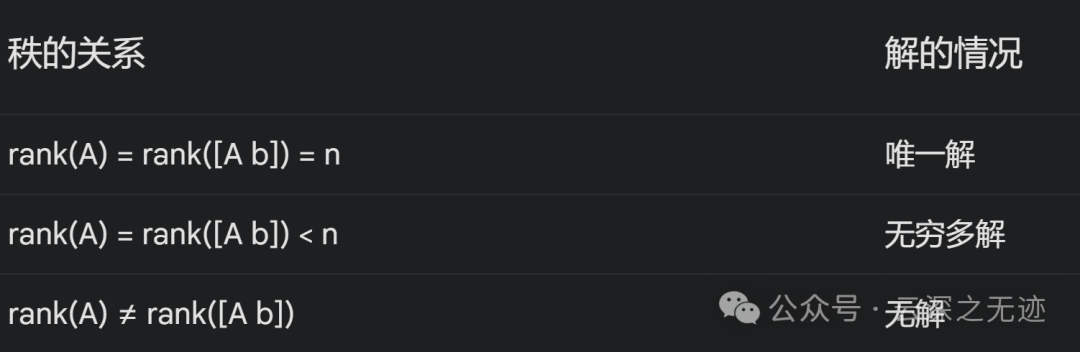
一个总结表
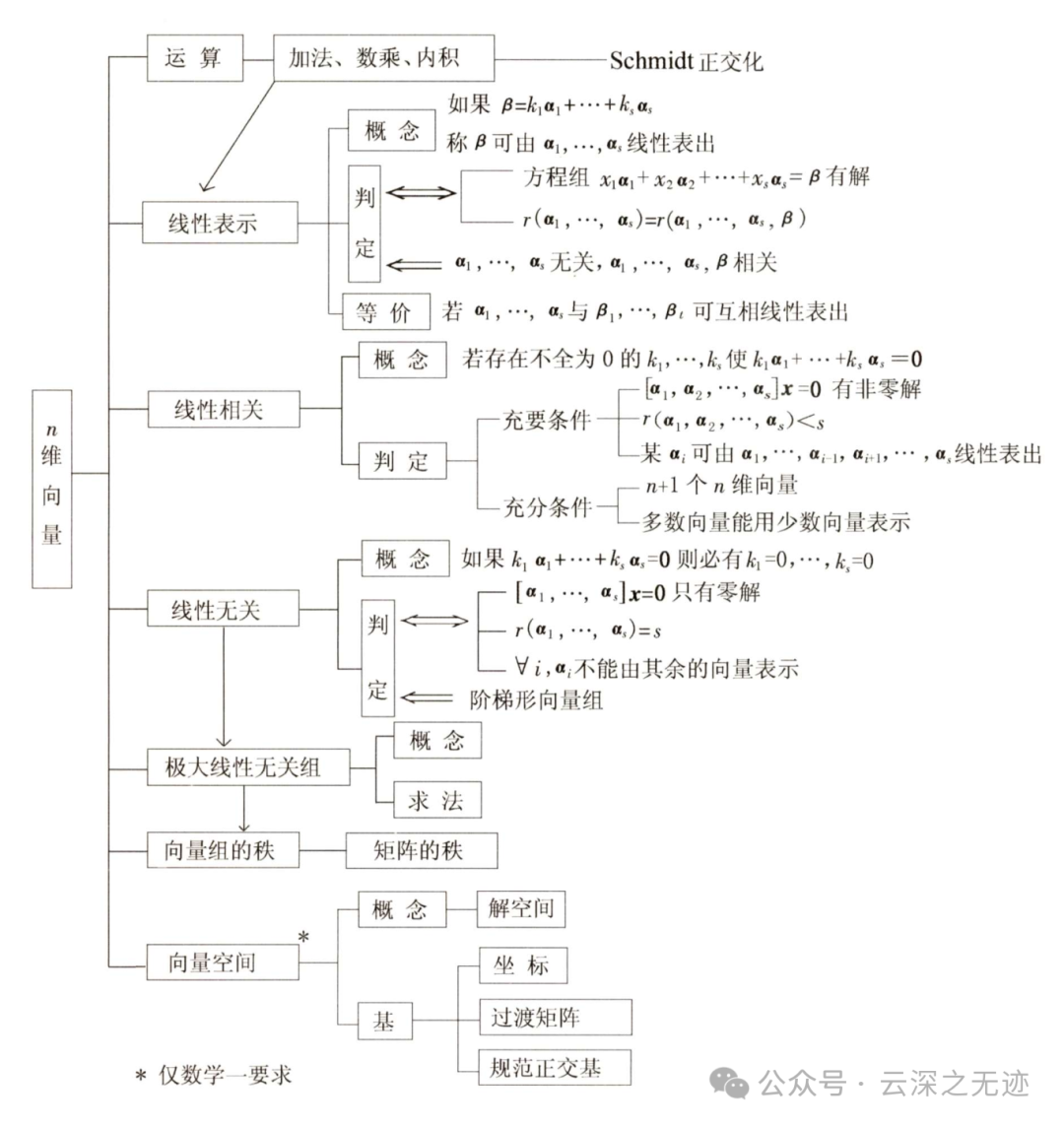
看知识网络出现了一个施密特正交矩阵
施密特正交化是一种将一组线性无关的向量组转化为一组正交基的方法。换句话说,它能将一组“倾斜”的向量组变成一组相互垂直的向量组,而这些新的向量张成的空间与原向量张成的空间相同。是一个逐步构造正交基的过程。
每次迭代,我们都从原向量组中选取一个向量,然后将其投影到已有的正交向量上,并减去投影部分,得到一个与已有的正交向量都垂直的新向量。

这就是向量,这种向量多了就是上面说的向量组

向量空间 是线性代数中最基础的概念之一,它是一个集合,在这个集合中定义了两种运算:向量加法 和 标量乘法。这两个运算需要满足一定的规则,使得这个集合具有线性空间的性质。
接着是子空间:
在向量空间中,子空间(subspace)指的是一个特殊的子集,这个子集本身也是一个向量空间。也就是说,这个子集中的向量进行加法和标量乘法运算后,结果仍然在这个子集中。
形象地说,子空间就像是一个向量空间中的“子世界”,它继承了原向量空间的线性结构。
一个集合W是向量空间V的子空间,当且仅当:
零向量包含在W中: 0 ∈ W
对加法封闭: ∀u, v ∈ W, u + v ∈ W
对标量乘法封闭: ∀u ∈ W, ∀c ∈ F (F为数域), cu ∈ W
其中,F为数域,通常是实数域R或复数域C。
零空间: 任何向量空间的零向量组成的集合就是一个子空间。
直线: 在二维平面中,过原点的直线就是一个子空间。
平面: 在三维空间中,过原点的平面就是一个子空间。
矩阵的列空间和行空间: 矩阵的列向量或行向量生成的子空间。
多项式空间: 所有次数小于等于n的多项式构成的空间是所有多项式空间的子空间。
整个空间V也是V的子空间
多个子空间的交集还是子空间
子空间的子空间也是原空间的子空间
我眼花了,这个子空间写的对吗?越看越不像。
基底 是向量空间中的一组特殊的向量。这组向量满足两个条件:
线性无关: 这一组向量中的任意一个向量都不能被其他向量的线性组合表示出来。
生成空间: 这一组向量可以线性组合出向量空间中的所有向量。
基底就像是一座大楼的骨架,它决定了整个大楼的结构。而向量空间中的所有向量,都可以看作是这座大楼中的房间,它们是由这些骨架构成的。
维数 是指向量空间的一个基底中向量的个数。一个向量空间的所有基底包含的向量个数是相等的,因此维数是一个确定的值。
形象地说,维数就像是这座大楼的层数,它决定了大楼的高度。
二维平面: 标准正交基 {(1, 0), (0, 1)} 是二维平面的一个基底。二维平面的维数是2。
三维空间: 标准正交基 {(1, 0, 0), (0, 1, 0), (0, 0, 1)} 是三维空间的一个基底。三维空间的维数是3。
完美的坐标是:规范正交基 是向量空间中的一种特殊基。
正交性: 基向量两两垂直,即它们的内积为零。
规范性: 每个基向量的长度(模)为1,即它们是单位向量。
规范正交基就像是一组相互垂直且长度为1的坐标轴,它们构成了一个完美的坐标系。
解空间 :是指线性方程组的所有解的集合。准确说,对于一个齐次线性方程组 Ax = 0,它的解空间是所有满足这个方程的向量x的集合。
还有一段,
过渡矩阵 (Transition Matrix) 描述了向量空间中不同基之间的一种变换关系。

就是这样的
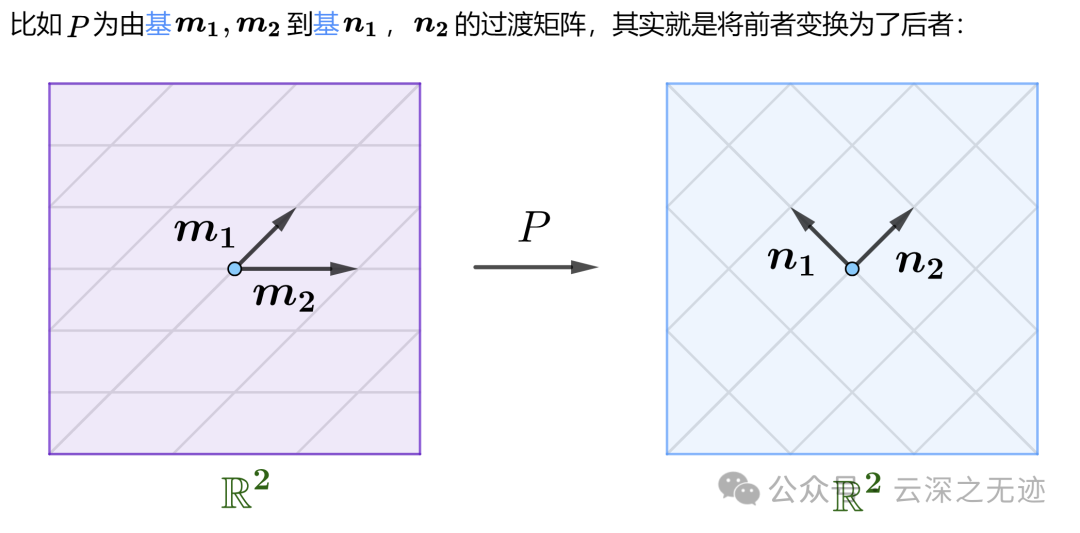
变换,变换了两个基底
旧基:
新基:
那么,过渡矩阵 就是一个 的矩阵,它的每一列都是新基的向量 在旧基 下的坐标。
过渡矩阵就是一本“字典”,它告诉我们如何将一个向量在新基下的坐标转换为旧基下的坐标,反之亦然。
过渡矩阵是可逆矩阵。
本来到这里我就解决问题了,但是是难得的好机会,再写一点。
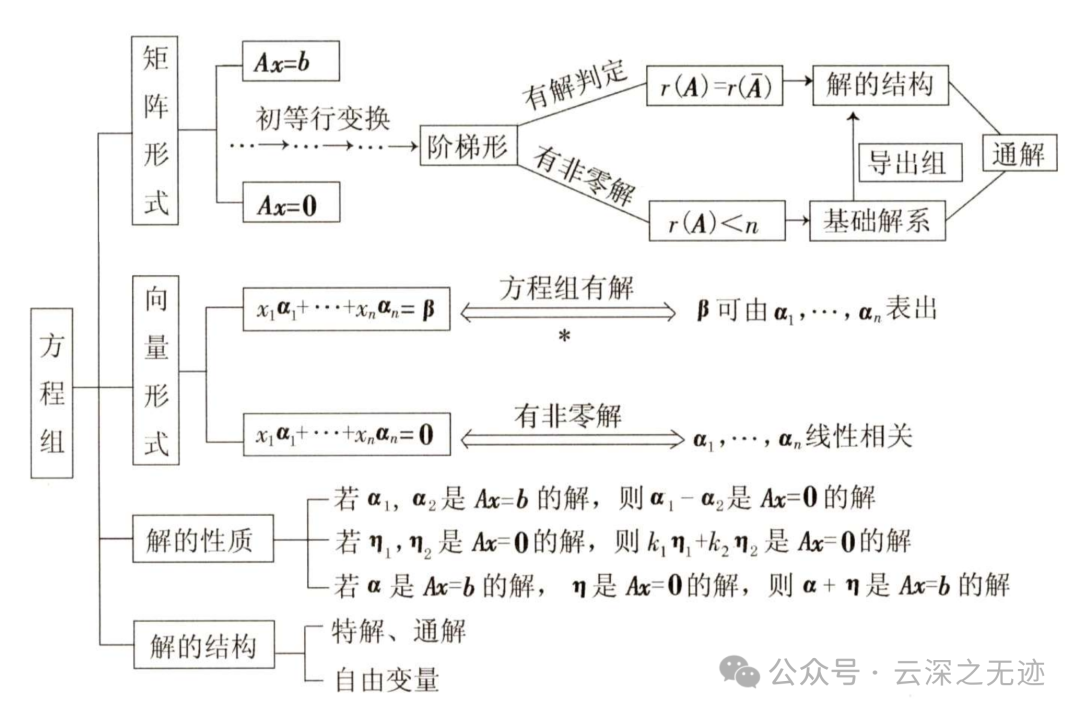
解方程
非齐次线性方程组就是形如 Ax = b 的方程组,其中 A 是系数矩阵,x 是未知向量,b 是常数向量。
与齐次线性方程组(即 b=0 的情况)不同,非齐次方程组的常数项不全为零。
设 A 是 m × n 矩阵, b 是 m × 1 矩阵,则非齐次线性方程组 Ax = b 有解的充分必要条件是:秩相等 r(A) = r(A|b),其中 (A|b) 是增广矩阵。
这里其实和上面的N维向量组,大同小异,我们就直观来看。有解就是说可以被表示出来,线性无关存在了,但是这个线性无关的到底有多少才是感兴趣的。
秩相等意味着什么: 当 r(A) = r(A|b) 时,说明增广矩阵中加入常数向量 b 后,没有产生新的线性无关的行。换句话说,常数向量 b 可以由系数矩阵 A 的列向量线性表示,即方程组有解。
秩相等是方程组有解
齐次方程组的解空间: 对于非齐次方程组 Ax = b,对应的齐次方程组 Ax = 0 的解空间是一个向量空间。
非齐次方程组的解: 非齐次方程组的一个特解加上齐次方程组的任意一个解,就是非齐次方程组的一个解。
齐次方程组的解空间就像是一条过原点的直线或平面。
非齐次方程组的特解就像是一个不在原点上的点。
非齐次方程组的所有解就是过这个点并且平行于齐次方程组解空间的直线或平面。
无解: 当 r(A) ≠ r(A|b) 时,方程组无解。这个就很直观,加入的常数向量使得原来的无关向量变多了,就是类似出现了多解(可能在别的空间)
唯一解: 当 r(A) = r(A|b) = n (n为未知量的个数) 时,方程组有唯一解。这个没什么好说的。
无穷多解: 当 r(A) = r(A|b) < n 时,方程组有无穷多解。这个就是会出现自由变量。

高斯消元法: 将增广矩阵化为行阶梯形或简化行阶梯形,通过回代法求解。
矩阵的逆: 当系数矩阵 A 可逆时,方程组的解为 x = A⁻¹b。
非零行在所有零行的上方。
每一非零行的首非零元(称为主元)的列指标严格大于上一行非零行的首非零元的列指标。
主元所在列的其他元素均为零。
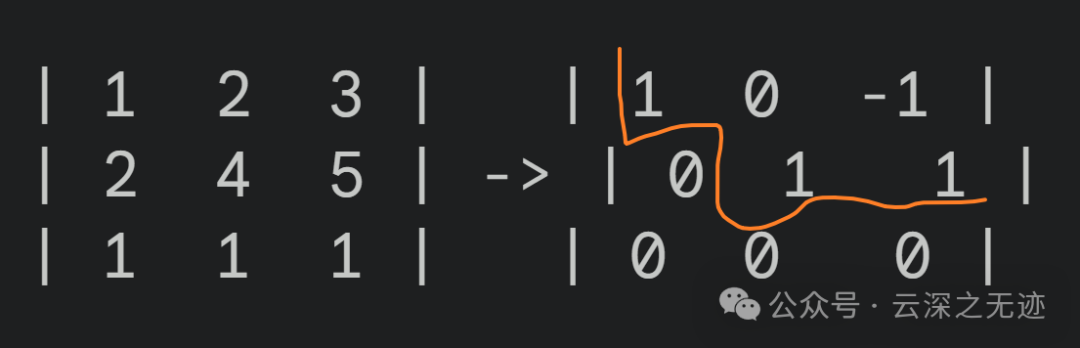
看第二行对比第一行就是往右移动了
行阶梯形矩阵就像是一座阶梯,每一阶的“台阶”都比上一阶的“台阶”向右移。
满足行阶梯形矩阵的所有条件。
每一非零行的主元为1。
主元所在列的其他元素均为0。
简化行阶梯形矩阵是将行阶梯形矩阵进一步简化,使得每一阶“台阶”的高度都为1,且“台阶”之间没有任何“斜坡”。
我觉得我是记住了,不知道你有没有记住。