(连续)离散时间,周期信号的傅里叶级数表示.完全推导版
信号与系统-时域分析-微分方程求解.茅塞顿开版
信号与系统漫谈-基础回顾
傅里叶级数-三种表达方式(双三角,余弦,复指数)
傅里叶级数-系数求解
纵观文章,其实还差一个级数到变换,赶紧复习补上。
首先我们熟知的是级数,是求和,是周期信号,但是我们放在更加普遍的地方看,非周期的连续信号才是主流,我们如何处理呢?因为傅里叶的分解特性太好了。
一个周期信号 𝑥~(𝑡) 的傅里叶系数 𝑎𝑘 能够利用 𝑥~(𝑡) 的一个周期内信号的傅里叶变换的等间隔样本来表示。
利用极限思想,周期信号演变成非周期信号,傅里叶级数演变成傅里叶变换。但无论是傅里叶级数综合式,还是傅里叶变换的综合式,其基本思想都是:将一般的信号分解为虚指数信号的线性组合。
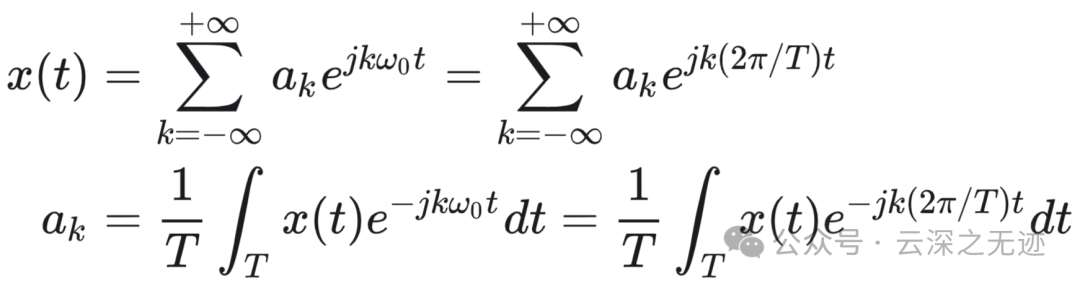
连续时间周期信号的傅里叶级数对

傅里叶级数与线性时不变系统
正弦信号: 理想的正弦波从负无穷大持续到正无穷大。
直流信号: 直流信号在整个时间轴上保持恒定,可以看作是频率为零的正弦波。
周期信号: 所有周期信号都可以看作是无限持续时间信号,因为它们在整个时间轴上重复出现。
傅里叶级数研究的对象是周期信号,周期信号必定是无限持续时间信号
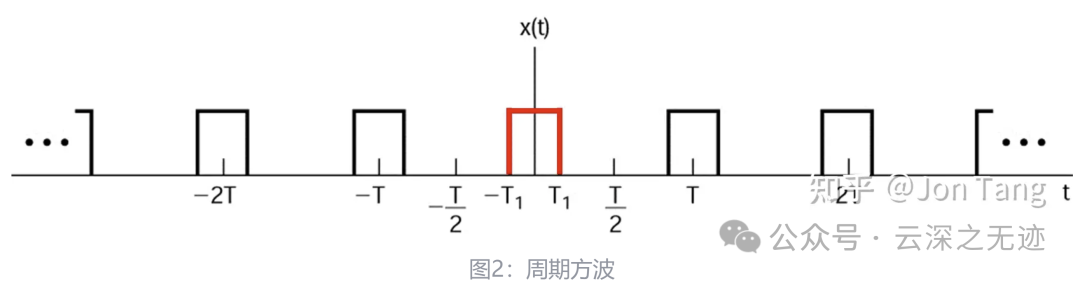
有限持续时间信号,顾名思义,就是在时间轴上只存在于有限的时间区间内的信号。也就是说,这种信号有明确的起始点和终点,在起始点之前和终点之后,信号的值为零。

其实还有个叫支撑信号的
脉冲信号: 在一个极短的时间内幅值很大,而在其他时间为零。
矩形脉冲: 幅值恒定,持续一段时间后突然降为零。
语音信号: 虽然语音信号的持续时间是有限的,但通常可以看作是多个有限持续时间信号的叠加。
在建立非周期信号的傅里叶变换时,可以把非周期信号当成一个周期信号在周期任意大时的极限来看待,并且研究这个周期信号傅里叶级数表示式 𝑇𝑎𝑘 的极限特性。
这里要说一下,周期信号就是一比一复制,那这个周期任意大的意思就是为了包容非周期信号,因为你总是要停下来的,那就把这个非周期的信号两边复制,形式上面还是周期信号。
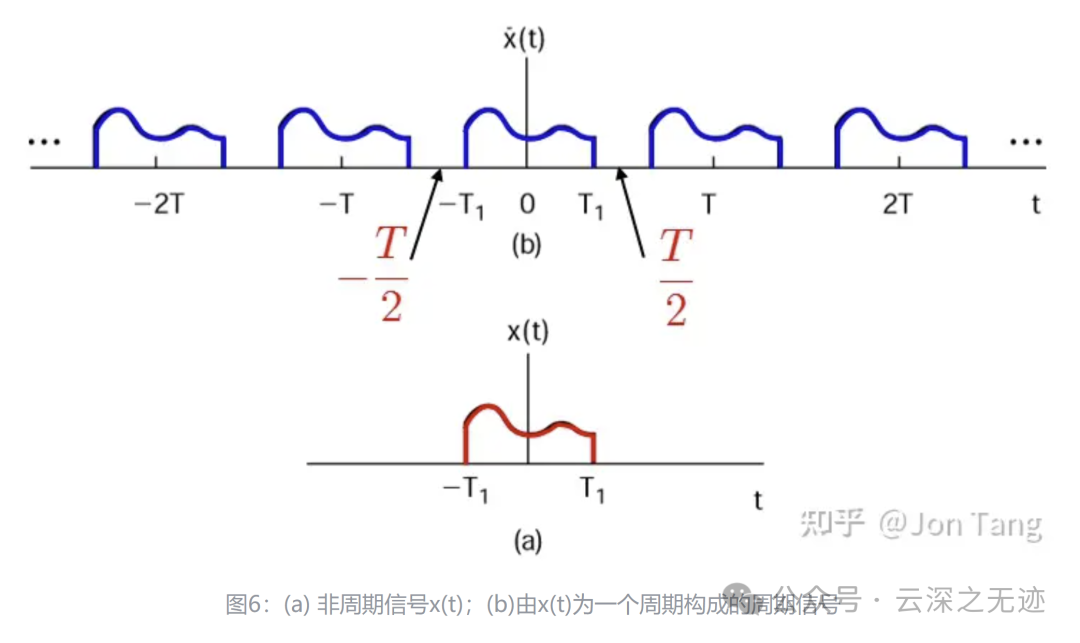
我又偷图啦
随着周期的增大,周期信号的频谱越来越密集,最终趋近于连续的频谱。
频谱,简单来说就是信号在不同频率上的分布情况。有两个谱:
幅度谱: 表示信号在不同频率下的幅值大小。
相位谱: 表示信号在不同频率下的相位
还有不同的频谱:
连续时间傅里叶变换(CTFT): 用于分析连续时间信号的频谱。
离散时间傅里叶变换(DTFT): 用于分析离散时间信号的频谱。
离散傅里叶变换(DFT): 是DTFT的离散形式,广泛应用于数字信号处理中。
快速傅里叶变换(FFT): 是DFT的快速算法,大大提高了计算效率。
傅里叶变换的表达式实际上就是周期无限大时傅里叶级数系数的极限形式。
这里可能是理解的关键,我还是要费些口舌。
傅里叶级数的频谱是离散的,因为只有整数倍的基频。
当周期趋于无穷大时,这些离散的频率点会越来越密集,最终形成一个连续的频谱,这就是傅里叶变换的频谱。
傅里叶级数是将函数表示为一个无穷级数,即对所有谐波分量进行求和。
当周期趋于无穷大时,求和变为积分,这就是傅里叶变换的积分形式。
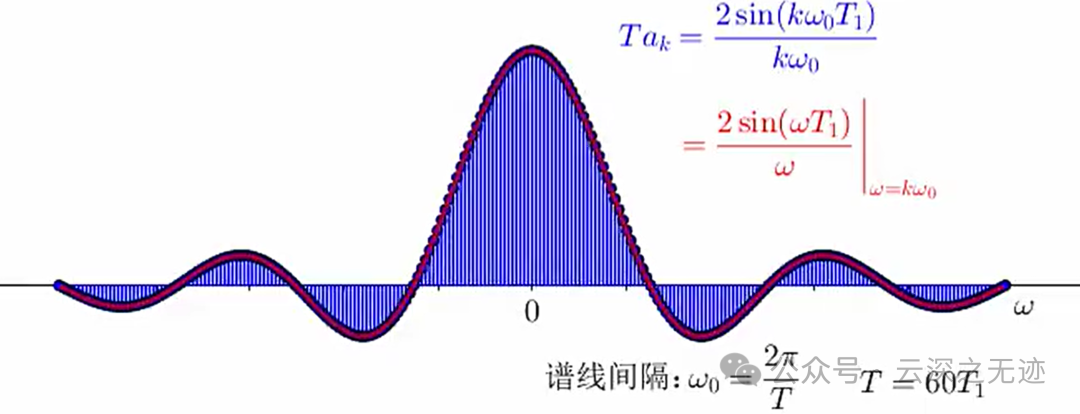
2Π是区间长度,T是上面说的无限,这个公式的w可不就超级小了
我们可以将傅里叶级数看作是将一个连续的信号分割成一个个的小片段,然后用一系列的正弦波去拟合这些小片段。当周期趋于无穷大时,这些小片段变得越来越小,最终就变成了一个连续的信号,而傅里叶变换就是用来描述这个连续信号的频谱成分
傅里叶级数系数的表达式:对于一个周期为T的周期函数x(t),其傅里叶级数系数c_n的表达式为:
c_n = (1/T) * ∫[0,T] x(t) * exp(-j*n*ω_0*t) dt其中,ω_0 = 2π/T是基波角频率。
周期T趋于无穷大:当周期T趋于无穷大时,基波频率ω_0趋近于零,离散的频率分量nω_0变得越来越密集,最终形成连续的频谱。同时,傅里叶级数系数c_n也发生变化。
引入连续频率变量ω:为了描述连续的频谱,我们引入连续的频率变量ω。令ω = nω_0,则当T趋于无穷大时,n趋于无穷大,Δω = ω_0趋于无穷小。
将上述结果代入傅里叶级数系数的表达式中,并取极限,得到傅里叶变换X(ω)的定义:
X(ω) = ∫[-∞,+∞] x(t) * exp(-jωt) dt学习要细致,不知道有没有看见基波角频率这个东西?
基波角频率就是基波的角频率。下·hhhh,车轱辘话了。
ω₀ = 2π/Tω₀:基波角频率
T:周期
基波角频率,形象地说,就是在一个周期性变化的系统中,最慢的那个变化的速度。它就像一个钟摆的摆动频率,是这个系统最基本的振动频率。
周期信号: 一个周期性信号,就是说它的波形会不断重复出现。比如,正弦波、方波等都是周期信号。
基波: 在一个周期信号中,频率最低的那个分量,就叫做基波。基波决定了整个信号的周期。
角频率: 角频率是描述旋转运动的一种物理量,它表示单位时间内旋转的弧度数。在信号处理中,角频率用来描述信号变化的快慢。

傅里叶级数主要用于分析周期信号,将周期信号分解为一系列不同频率的谐波分量。它的频谱是离散的。
傅里叶变换则适用于周期信号和非周期信号,将时域信号变换到频域,表示信号在不同频率上的分布。它的频谱是连续的。
两者之间的关系:傅里叶变换可以看作是傅里叶级数的推广。当周期趋于无穷大时,傅里叶级数中的离散频谱逐渐稠密,最终形成连续的频谱,即傅里叶变换。
傅里叶系数表示每个谐波分量的幅值和相位。
傅里叶变换的结果是一个复数函数,其模值表示信号在对应频率上的幅值,相位表示信号在该频率上的相位。
傅里叶变换: 一个脉冲信号的傅里叶变换是一个频谱分布在整个频域的 sinc 函数。
我们就这再看唐老师的课程,其实就是上面我说的这句话的延拓,这次看看能不能讲明白其中的困惑。
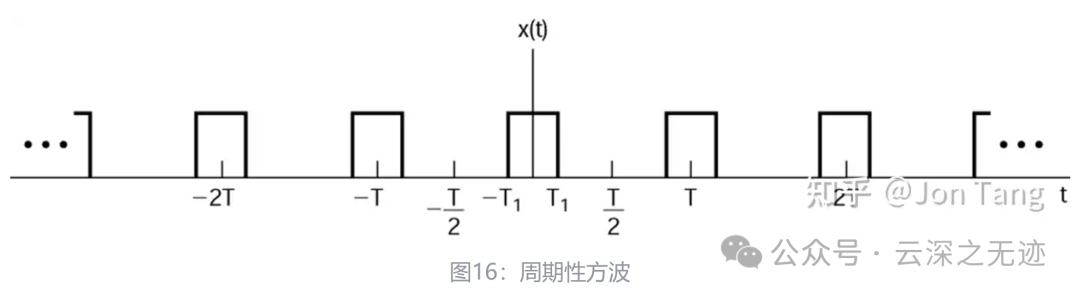
这个特殊是因为他是一个方方正正的信号,其次也是通讯里面的一个码元,就是表示1的信号。你还记得SPI,IIC里面的0.1是什么样的吗?其实就是这个东西。
他的名字也叫,连续周期信号,无限持续信号。
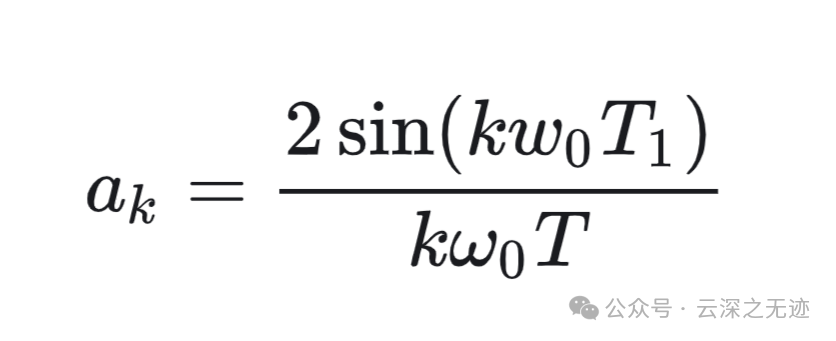
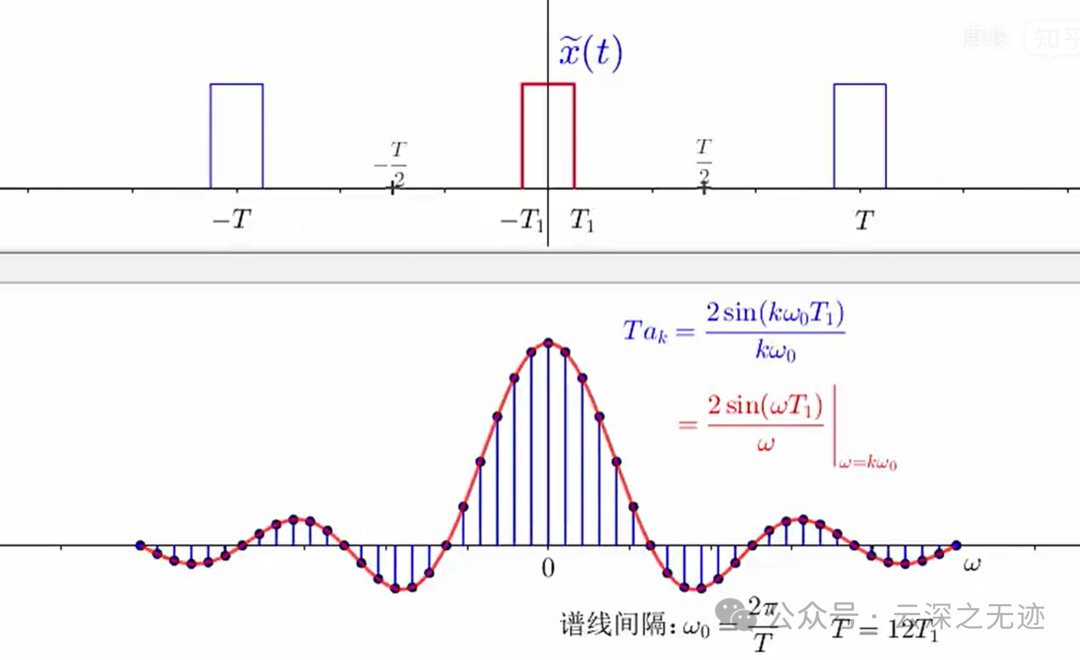
这是他的傅里叶级数的系数
其中 𝜔0=2𝜋/𝑇 。对于 𝑇=4𝑇1,𝑇=8𝑇1 和 𝑇=16𝑇1时有,也就是把下面的分母扩大了,角频率就变小了,也就是更精密了。
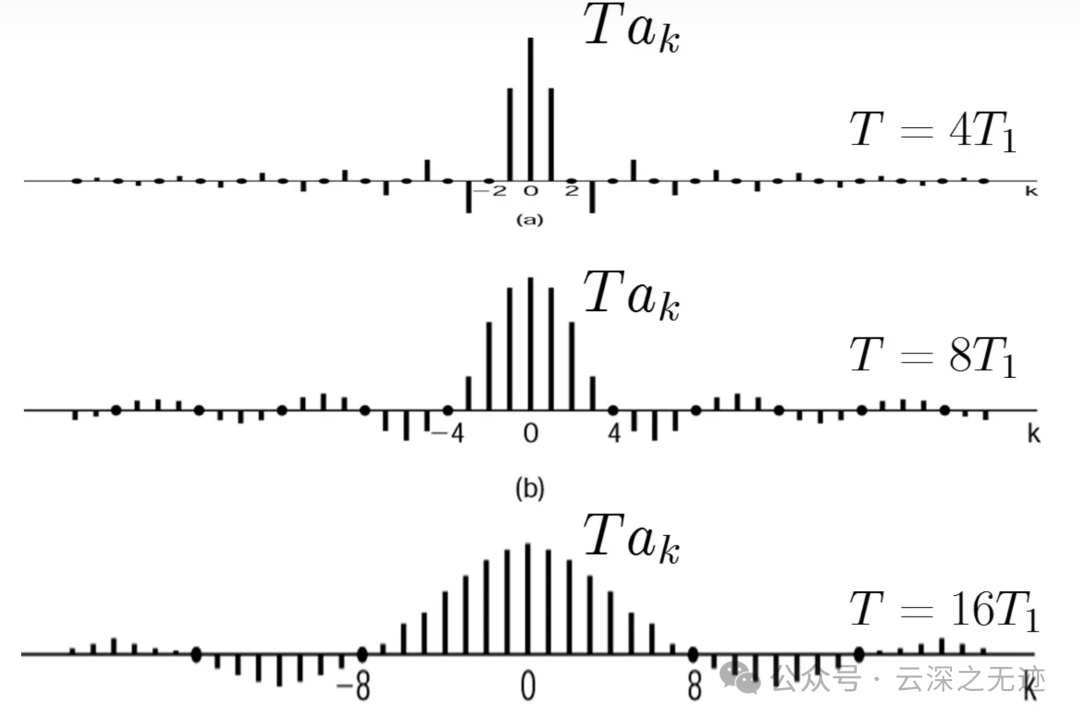
没问题是吧?
这里难的地方在于这个坐标系axis上面的表示方法。
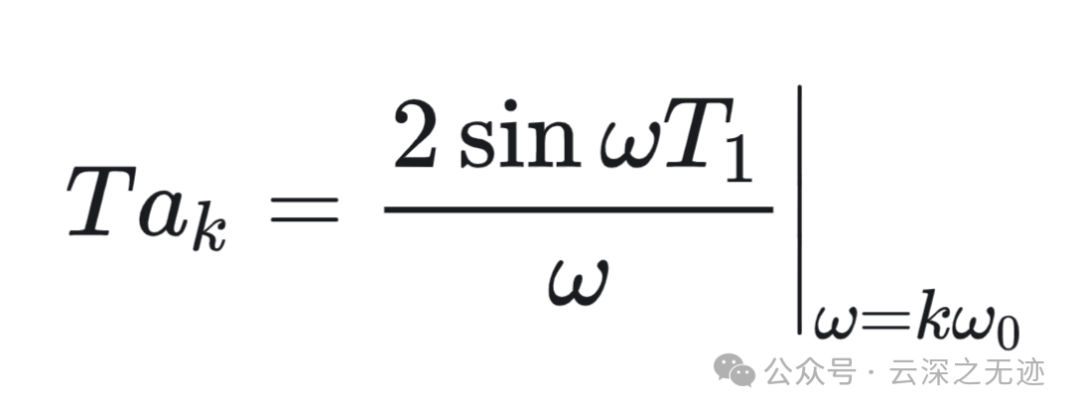
我们也可以把上面的系数看成一个对连续包络函数采样后的离散样本
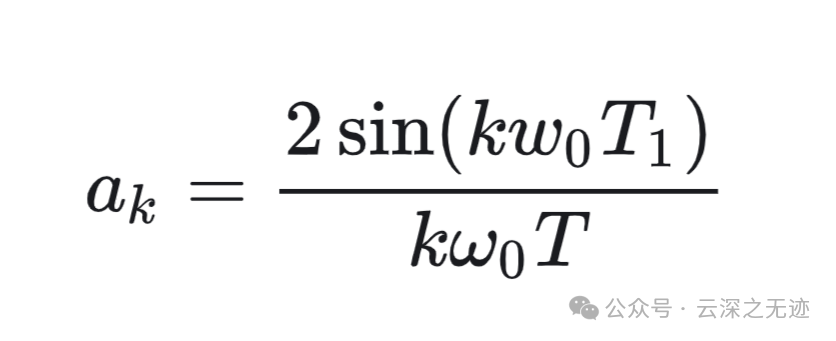
变换就在于把上面的k,k的含义是第几个谐波的意思。把它和角频率卸载了一起,这样就可以在形式上面统一起来,看下面的分母就是一个w。
若将 𝜔 看成一个连续变量,则函数 (2sin𝜔𝑇1)/𝜔 就代表 𝑇𝑎𝑘 的连续包络,这些系数就是在此包络上等间隔采样所得的样本。
连续包络: 当我们将角频率 ω 看作一个连续变量时,函数 (2sin(ωT₁))/ω 就描述了傅里叶系数 Ta_k 在频域上的分布情况。这个函数可以看作是 Ta_k 系数的连续包络线。
等间隔采样: 实际的傅里叶系数 Ta_k 就是在这个连续包络上,以 kω₀ 为间隔进行采样得到的离散点。
与周期 T 的关系: 如果 T₁ 是一个固定值,那么这个连续包络的形状就只与 T₁ 有关,而与信号的周期 T 无关。
是不是还不清楚,这样看!
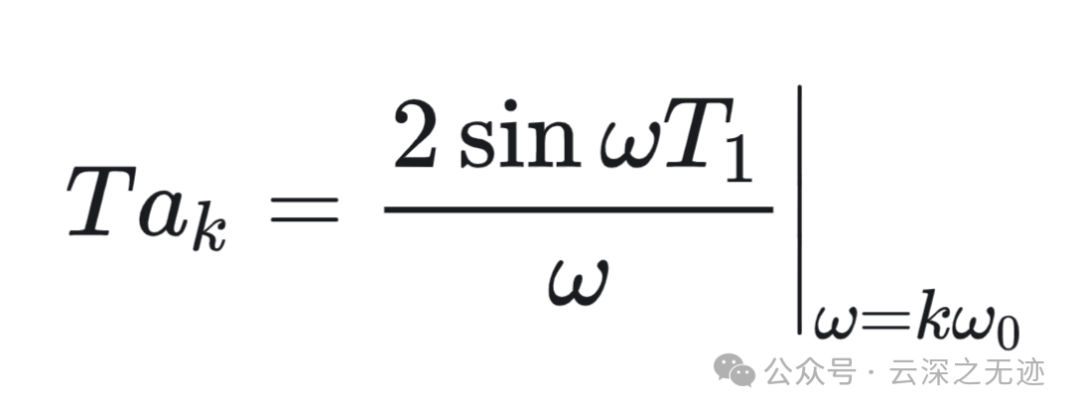
在这个公式里面,T1现在就当是固定的量了,不变化,而ω是变量也就是文中说的,包络与T无关。
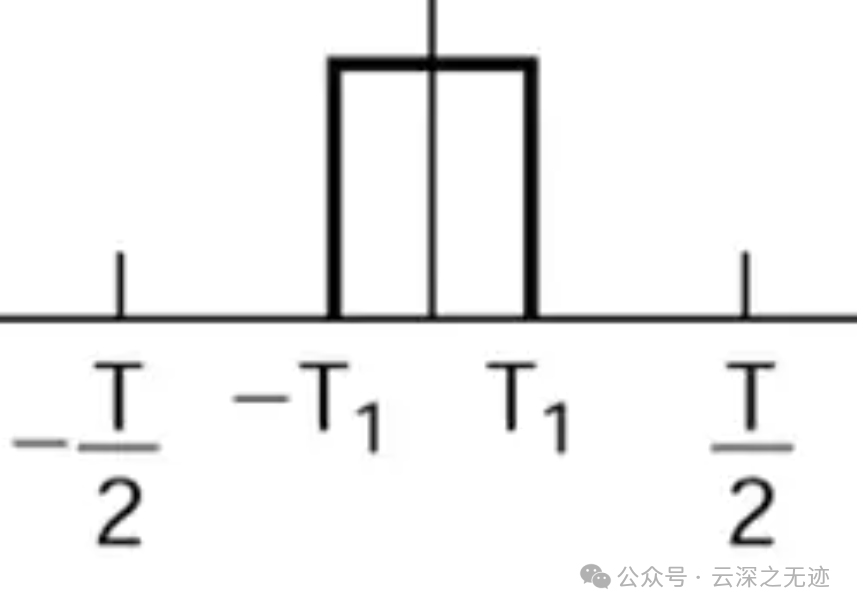
那T1是什么?就是方波的一半罢了。
这次看下面的结论就是很通畅了。
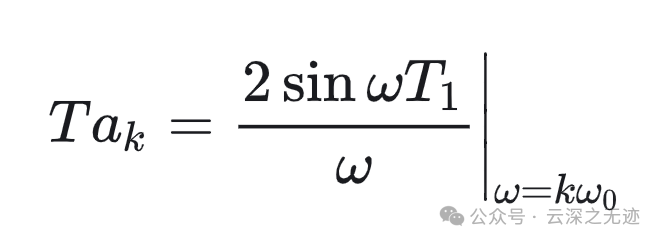
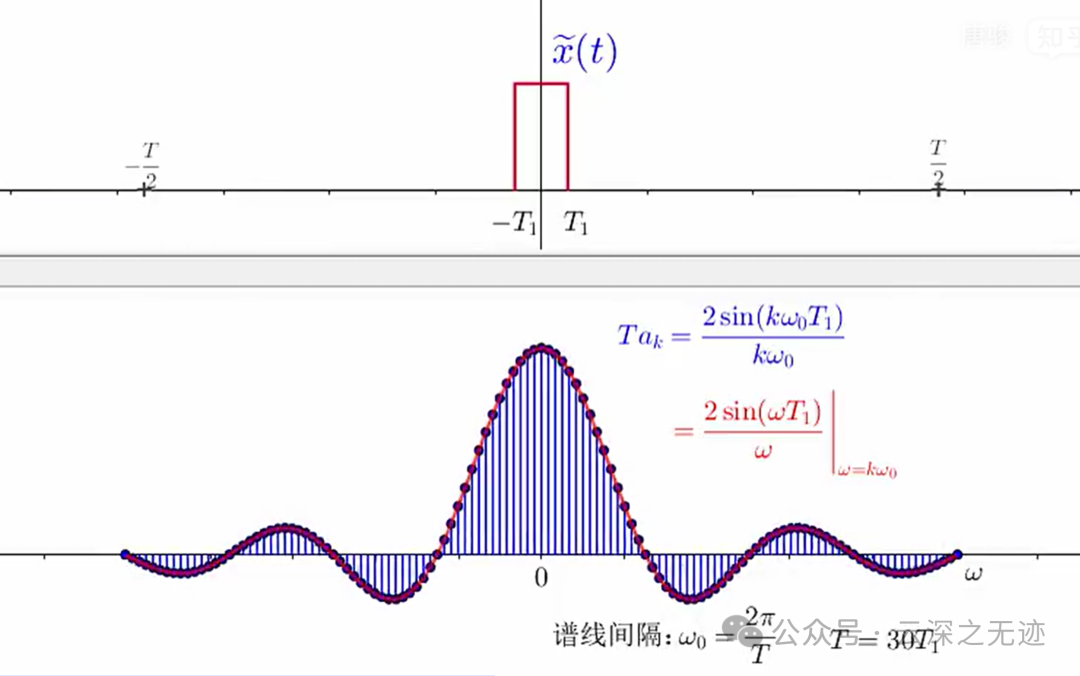
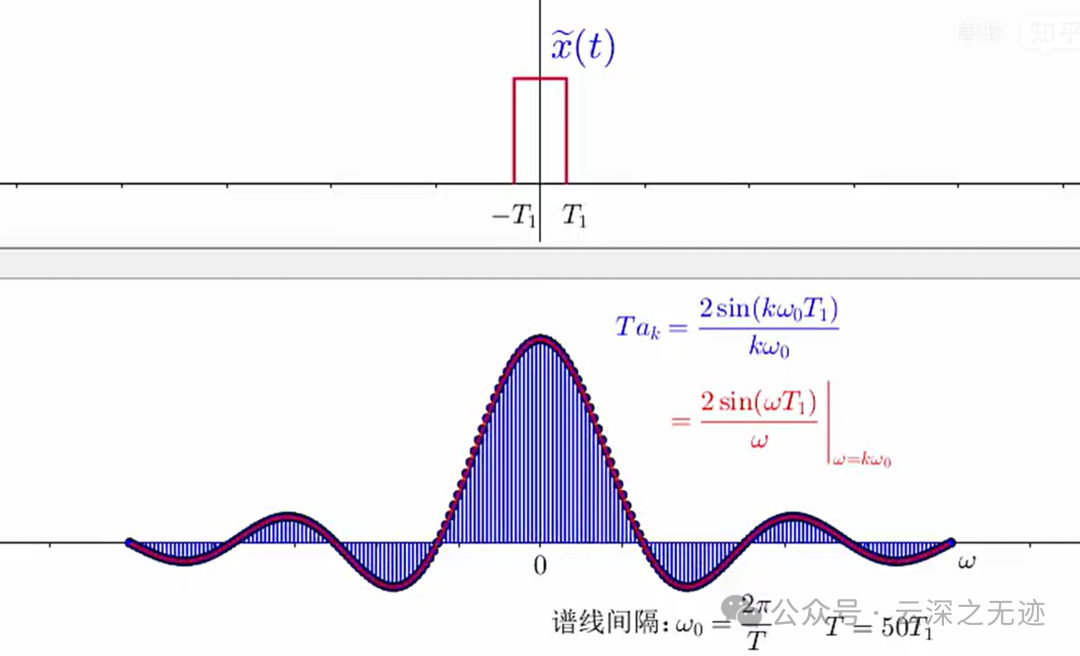
但这次是按式作为 𝑇𝑎𝑘 包络的样本给出的。从该图可以看到,随着 𝑇 增加(或等效地,基波频率 𝜔0=2π/𝑇 减小),该包络就被以越来越密集的间隔采样。
随着 𝑇 变成任意大,原来的周期方波就趋近于一个矩形脉冲(也就是说,在时域保留的是一个非周期信号,它对应于原方波的一个周期)。
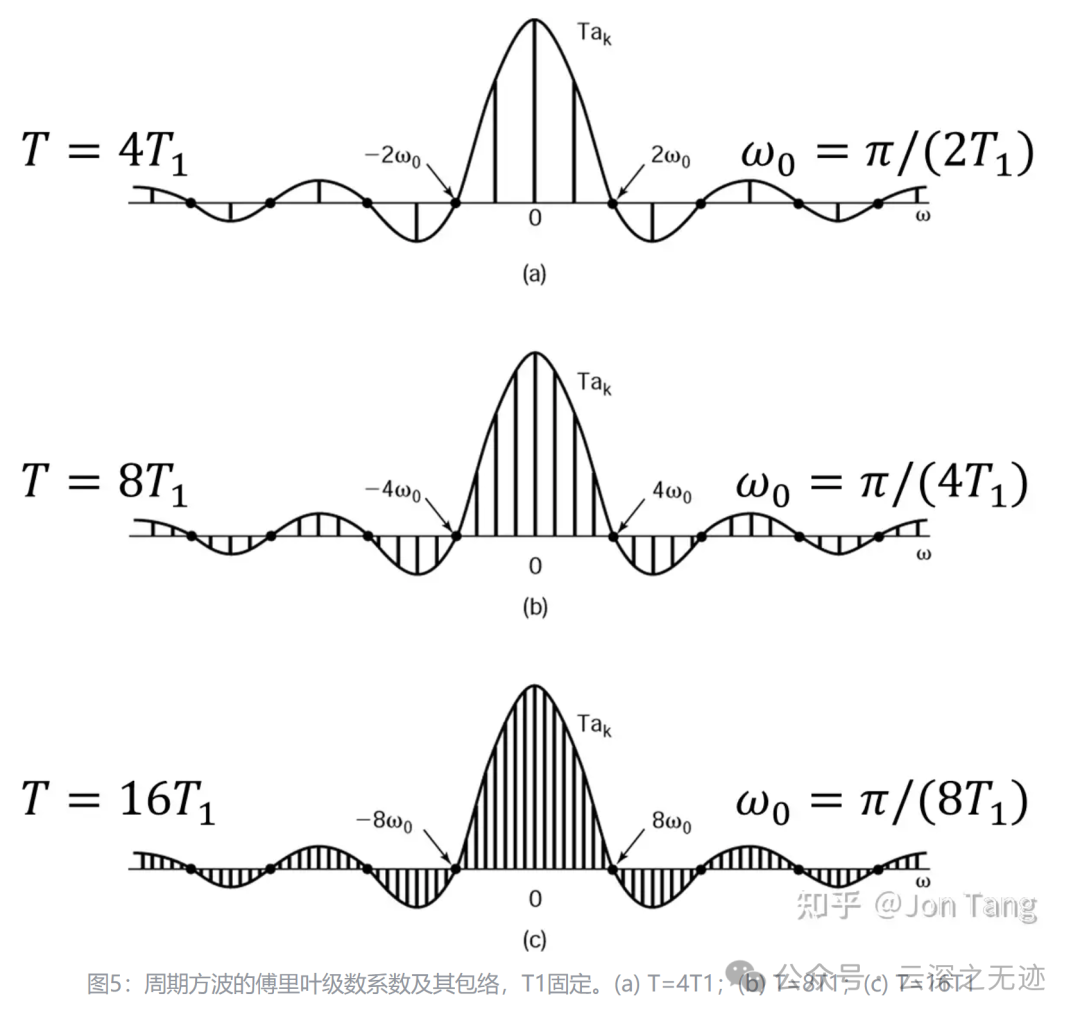
也就是T1固定就是固定了外面的样子,里面被无限的分割
与此同时,傅里叶级数系数(乘以 𝑇 后)作为包络上的样本也变得越来越密集,这样从某种意义上说,随着 𝑇→∞ ,傅里叶级数系数(乘以 𝑇 ),即 𝑇𝑎𝑘 就趋近于这个包络函数。
再次提醒坐标系相关!
注意图 横轴的变量:
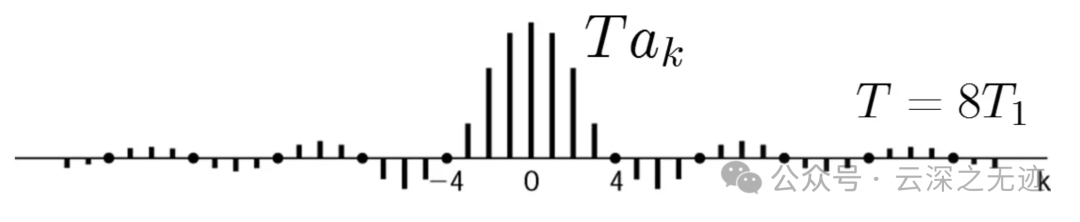
图中的横轴变量是 𝑘 ,表示谐波次数-1
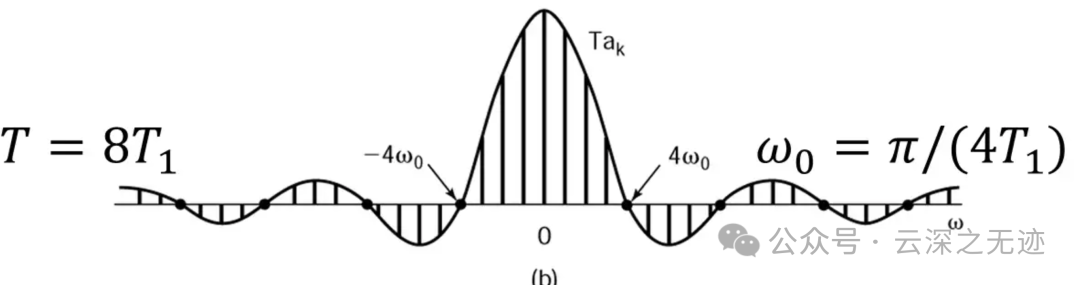
图横轴的变量是 𝜔 -2
事实上,图-1横轴变量 𝑘 既然是表示“第 𝑘 次谐波”,其实隐含的是 𝑘𝜔0 ,只是隐去基波频率 𝜔0 而只保留 𝑘 ,这也是为什么称傅里叶级数系数 𝑎𝑘 是信号的“频域表示”,原因就是因为它其实隐含着 𝑘𝜔0 ,横轴对应着频率含义。
再次总结:在建立非周期信号的傅里叶变换时,可以把非周期信号当成一个周期信号在周期任意大时的极限来看待,并且研究这个周期信号傅里叶级数表示式 𝑇𝑎𝑘 的极限特性。
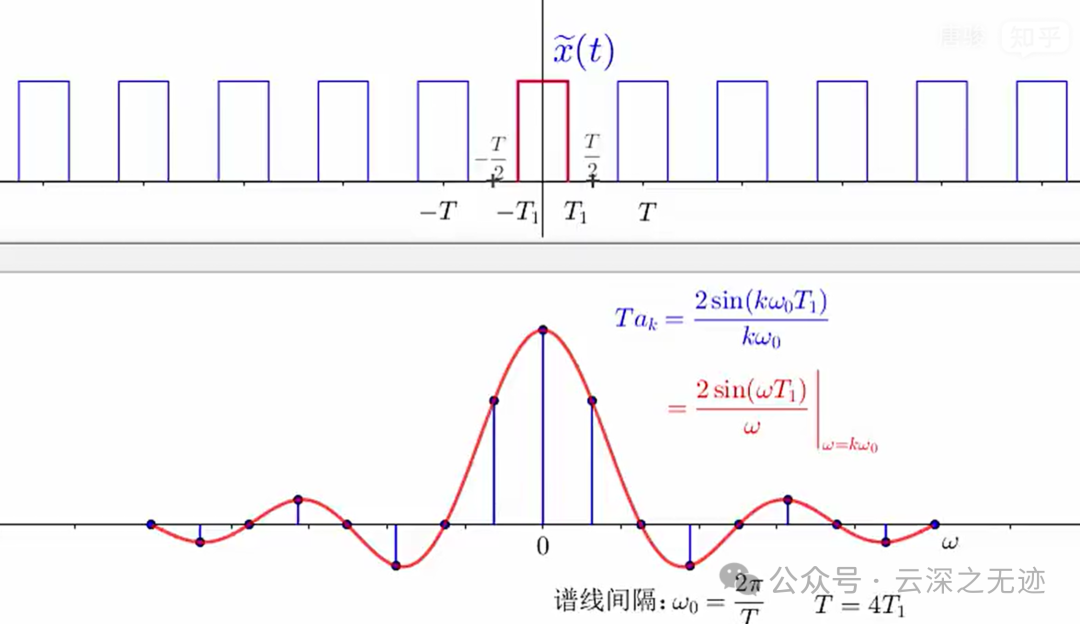
若干图示
周期为 𝑇 的方波信号 𝑥~(𝑡) 随着周期 𝑇 越来越大,傅里叶级数系数的间隔 𝜔0=2𝜋/𝑇 越来越小,随着 𝑇→∞ ,周期信号就变成了非周期信号;相应地, 𝜔0→0 ,此时相邻的傅里叶级数系数 𝑎𝑘 就“粘在一起”,于是 𝑇𝑎𝑘 就变成了连续函数。
其实我们目前为止还是没有给出结果,还是得写点,我都想去吃饭了。
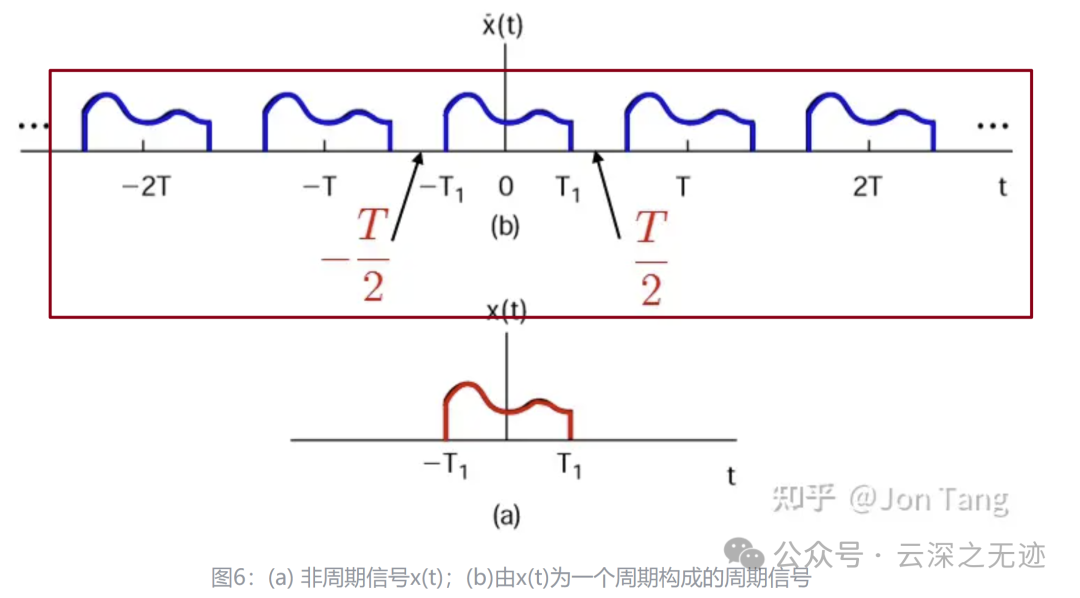
看第一个图,周期信号,可以给出一个傅里叶的级数对:
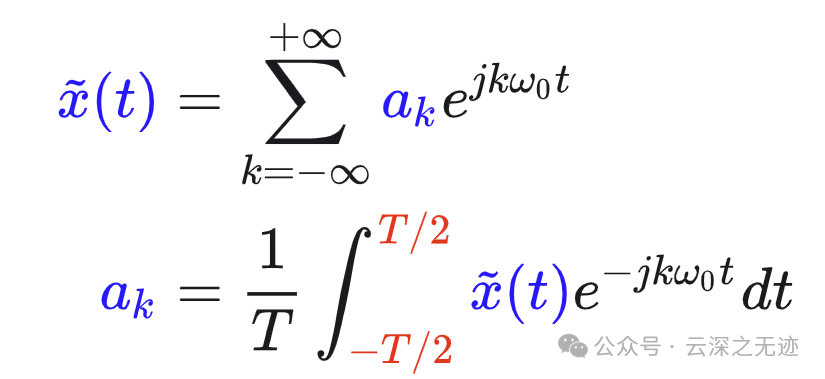
注意到式的积分区间是 −𝑇/2∼𝑇/2 ,而在此区间内,有 𝑥(𝑡)=𝑥~(𝑡) ,所以也可以写成:
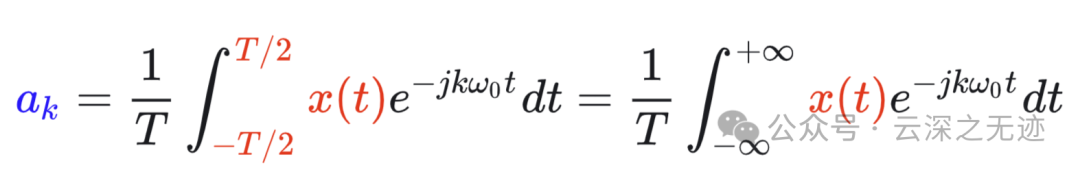
第二个等号成立是因为 𝑥(𝑡) 在区间 −𝑇/2∼𝑇/2 之外都为 0
就这样,因为后面都是0都不影响了,所以无限也就无所屌谓哦
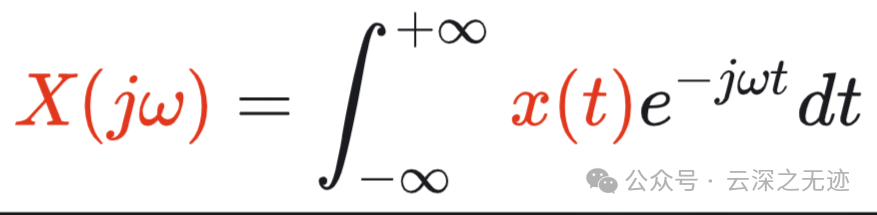
定义 𝑇𝑎𝑘 的包络 𝑋(𝑗𝜔) 为:
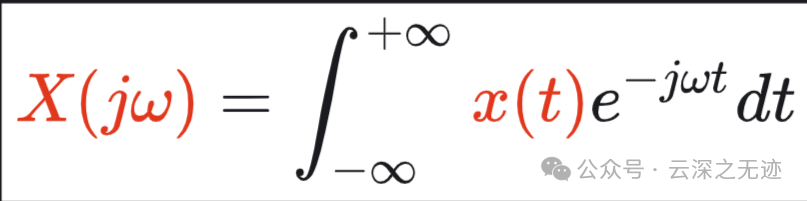
这里文章中没有说清楚,这是傅里叶变换的定义式。
它将时域信号 x(t) 转换为频域信号 X(jω)。X(jω) 表示信号 x(t) 在不同频率 ω 处的频谱成分。
Ta_k 通常表示傅里叶级数的系数,用于表示周期信号可以分解为一系列不同频率的正弦波的叠加。
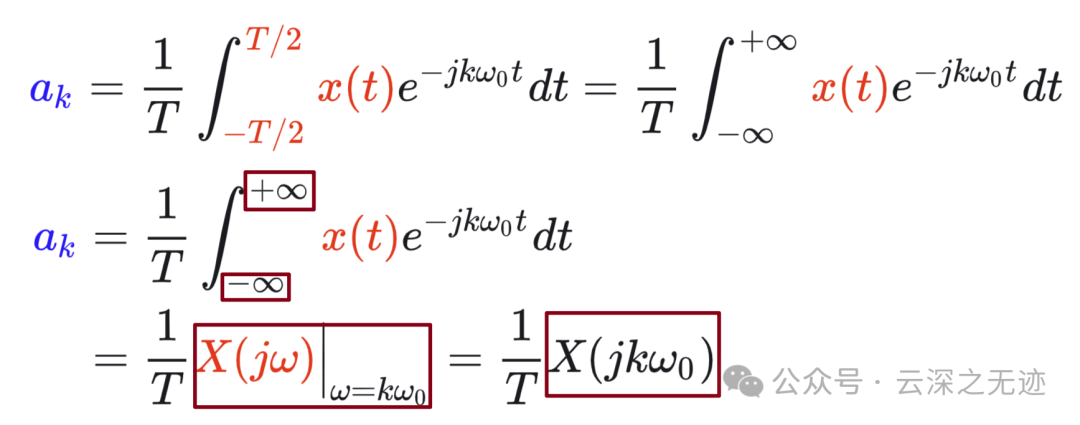
第一个是上面的周期信号的傅里叶级数中的分析式,第二个就是代入我们新写的公式的式子。
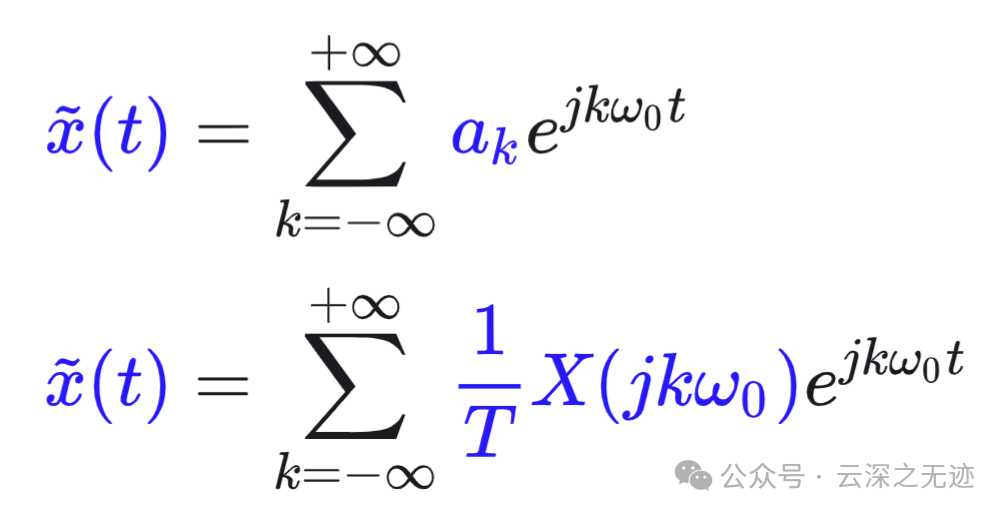
接着代入综合式
 :
:
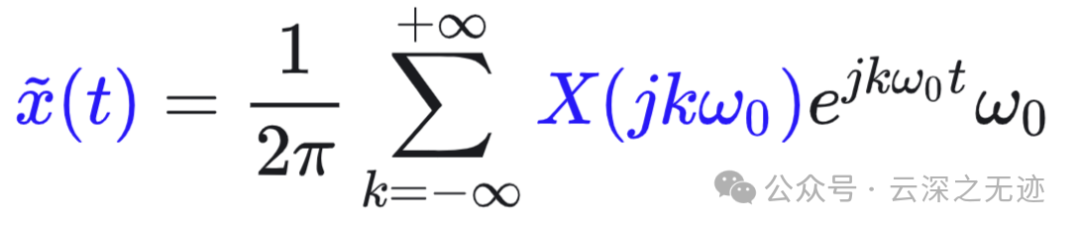
重写上面
接下来就是最难的数学部分了。现在考虑当周期 𝑇→∞ 将发生什么:
就是变成了一个大信号
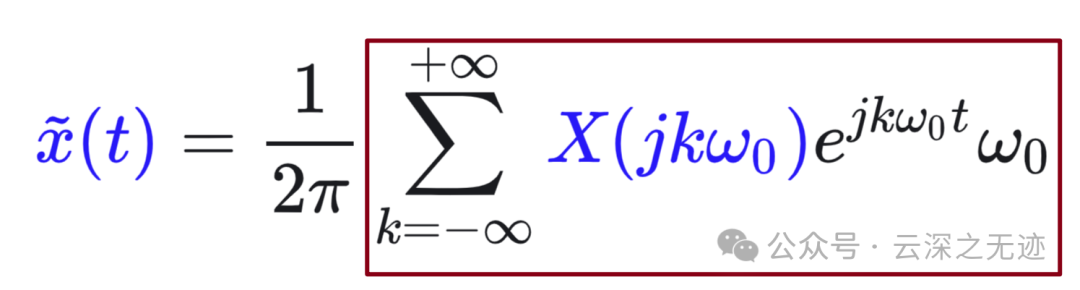
不难吧?
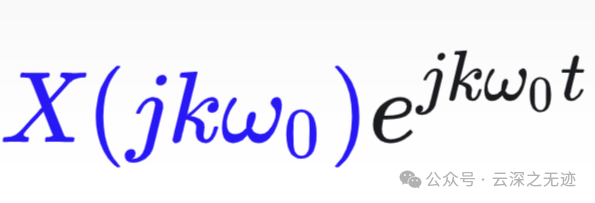
这个是一个矩形的高,宽是w0的矩形面积
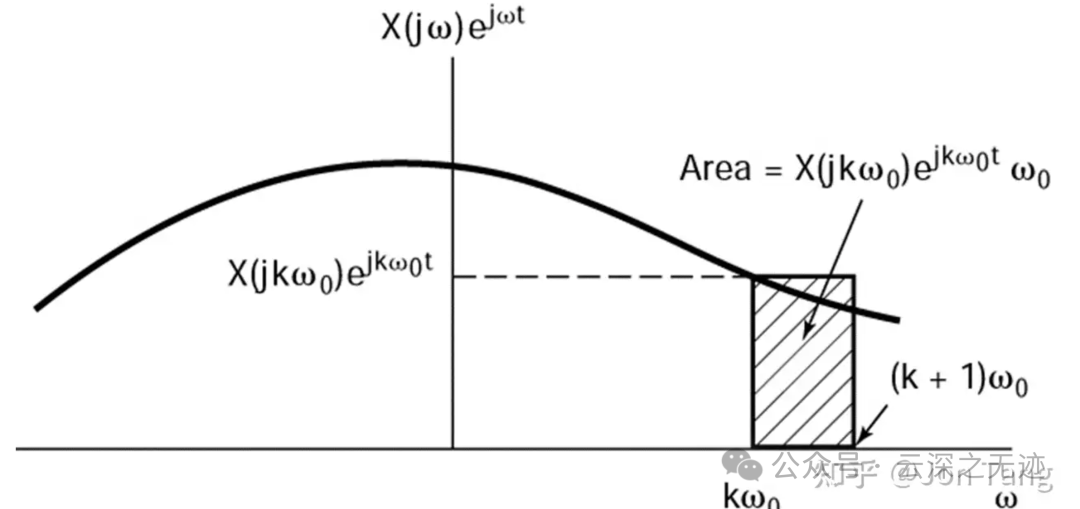
就是这样
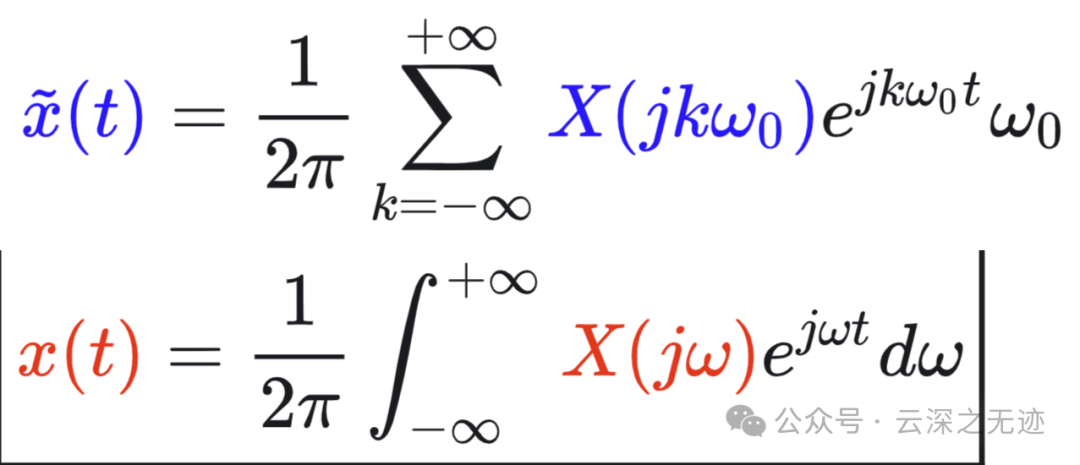
就变成了这样,是不是推出来了,变换来自于级数
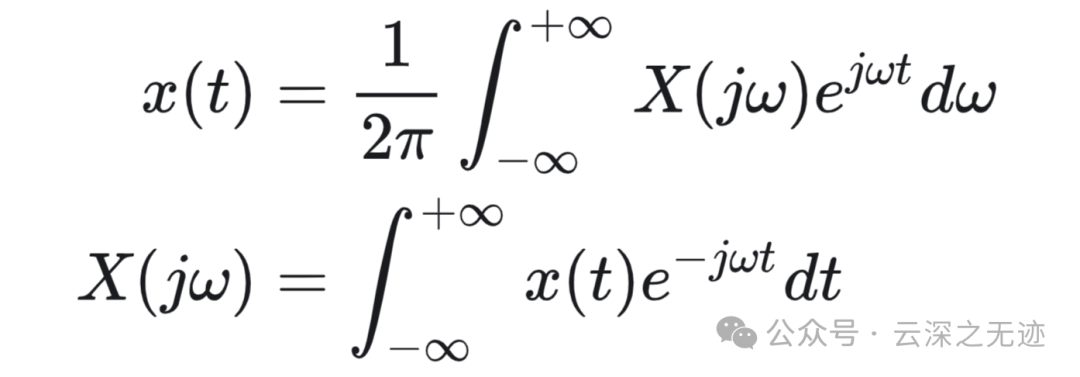
变换对理所当然的变成这样
这里还有更加精妙的结论,建议是看书吧、
周期信号通过线性时不变系统的结论推广至非周期信号通过线性时不变系统。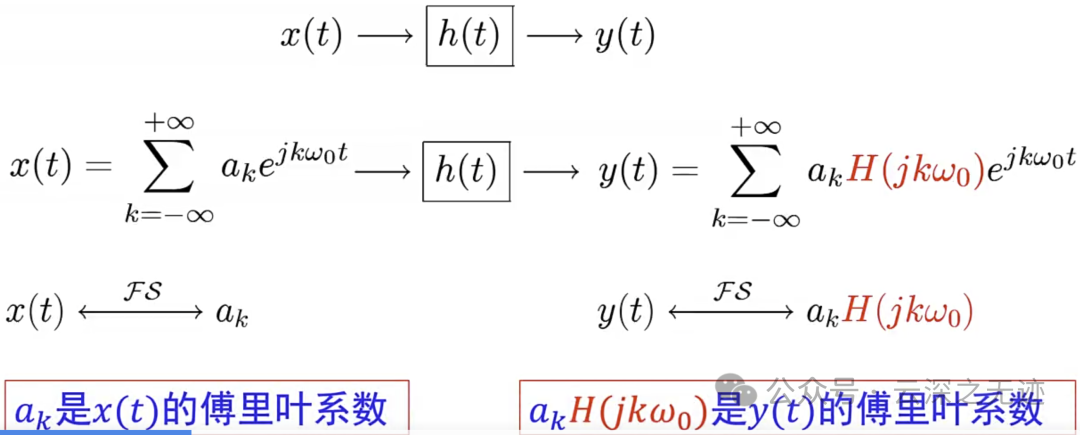
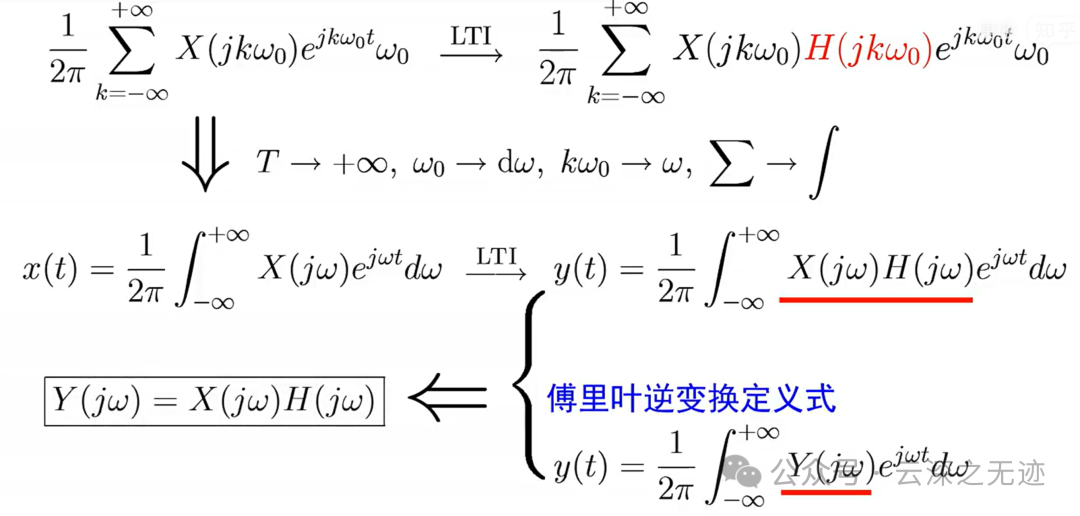
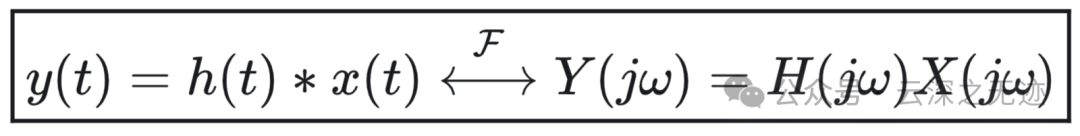
卷积性质证明
上式在信号与系统分析中十分重要。正如该式所表达的,它将两个信号的卷积映射为其傅里叶变换的乘积。
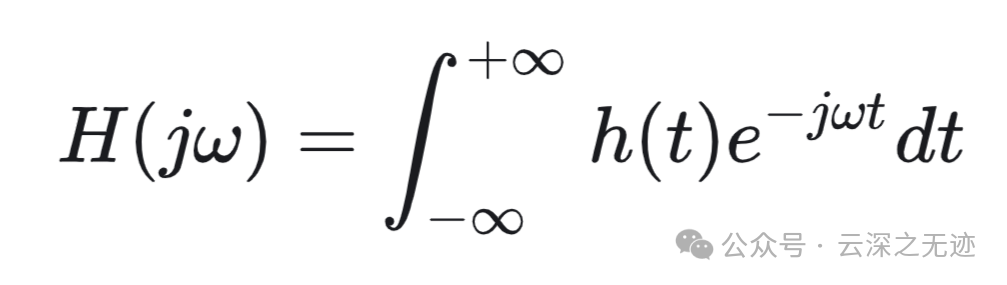
单位冲激响应的傅里叶变换 𝐻(𝑗𝜔) 是按傅里叶级数与线性时不变系统式所定义的频率响应。
频率响应 𝐻(𝑗𝜔) 控制着在每一频率 𝜔 输入傅里叶变换复振幅的变化。
在频率选择性滤波中,可以要求在某一频率范围内 𝐻(𝑗𝜔)≈1 ,以便让通带内的各频率分量几乎不受任何由于系统带来的衰减或变化;而在另一些频率范围内,可能要求 𝐻(𝑗𝜔)≈0 ,以便将该范围内的各频率分量消除或显著衰减掉。

一个纯时移系统的频率响应在所有频率上的模都为1,这意味着纯时移系统不会改变输入信号任何频率分量的大小:

后面是一些性质,地方有点不对。