事实上一切的开始都是傅里叶级数,都是内积,都是分解。
首先是连续时间,周期表示--->表示的是傅里叶的级数。
信号表示为一组线性移位单位脉冲的线性组合(这样就可以把信号分成了最简单的样子,然后合成的时候也简单,就是叠加就行)

之后又研究了一个指数函数通过一个LTI系统会被改造成什么样,发现就是这个指数函数成一个常数。
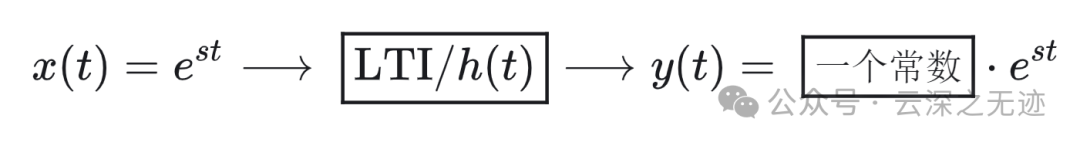
就是这样
发现了这么好的性质以后,就研究线性时不变系统对复指数信号的响应。
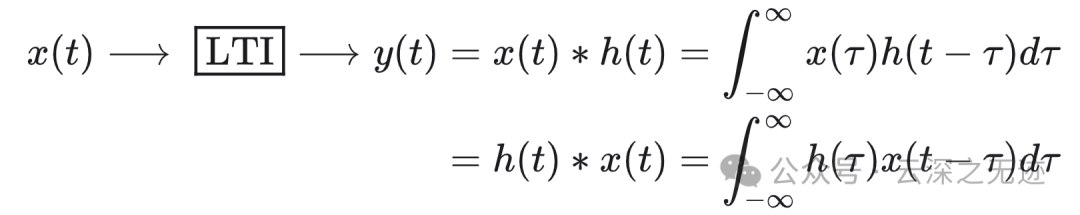
先通过任意的一个信号卷了两次(卷积的交换律)
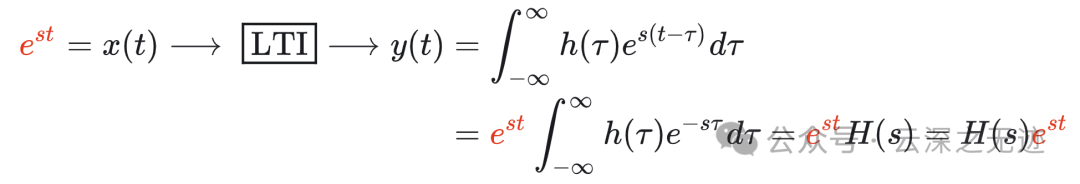
接着把信号换成复指数信号,发现了这个H乘以复指数信号是一个不变的形式,上面说是系统乘以一个常数,这里明显不是了。
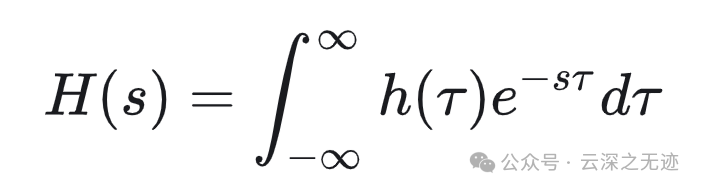
而是一个与系统单位脉冲响应 ℎ(𝑡) 有关的函数,故称之为系统函数
拉普拉斯出现了!
接着从内积的角度:
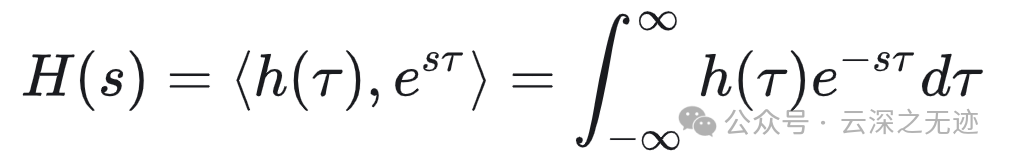
还是可以推回上式的,也就是说确实也是投影和分解的内核
LTI对指数信号特别偏爱,所以称指数信号是LTI系统的特征函数(连续时间信号也常被称为函数)与之对应的 𝐻(𝑠) 称为特征值。
因为看到了特征函数,就想到线性代数里面的特征值,在变换里面总有一些向量的方向不变(指在同一条线上)。

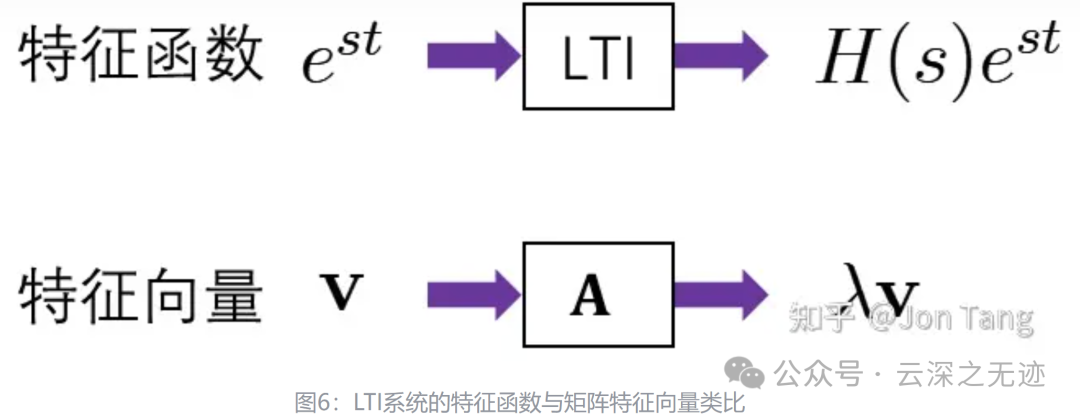
把最后一段话变成图就是这样
对,我们现在就是想,能不能在系统里面也是这样做?
将任意的信号 𝑥(𝑡) 表示为线性无关的特征函数的线性组合吗?
没错,就是这么想的,但如何定义函数的线性无关呢?
如果能找到一组正交的特征函数岂不更好?至少我们知道,正交的向量一定是线性无关的。
什么样的一组函数,既满足相互正交,又恰好是LTI系统的特征函数呢?

这个就是
https://zhuanlan.zhihu.com/p/558566593这里去看老师的专栏,不可能比奥本海默更精彩了。

现在也是相当于一个复指数的坐标系来对信号进行分解
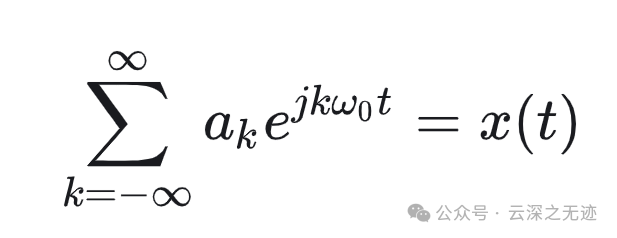
一个系数x单位坐标,求和
合成的 𝑥(𝑡) 是一个以 𝑇0 为周期的周期信号。
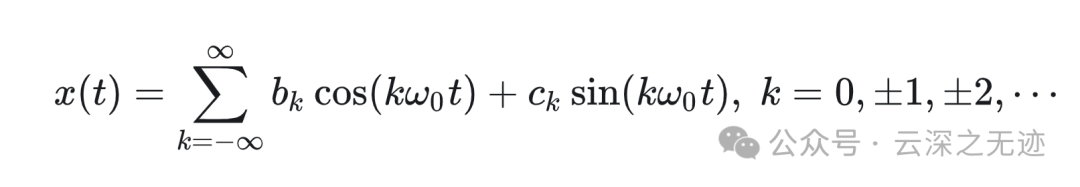
傅里叶把它展开了
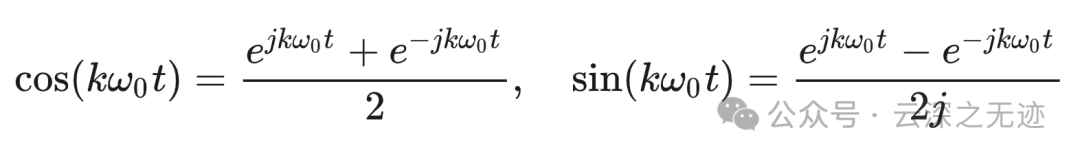
继续变换
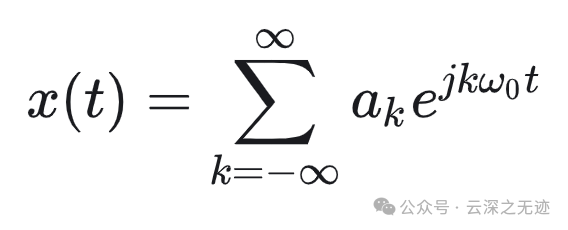
后面傅里叶就说了,任意的信号都可以展开成这样!
有些大佬就觉得,你这玩意圆乎乎的,肯定方波是模拟不来的!
谁说不行?拉格朗日中值定理,拉格朗日的反对当然不是出于个人恩怨,反对的理由听起来也很有道理:如图下所示的方波信号是不连续的,即存在间断点,而正弦和余弦函数都是连续函数,不可能用连续函数的线性组合完美表示间断函数。
事实上确实是拉格朗日对
连续时间周期信号的傅里叶级数表示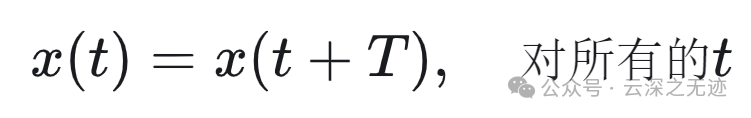
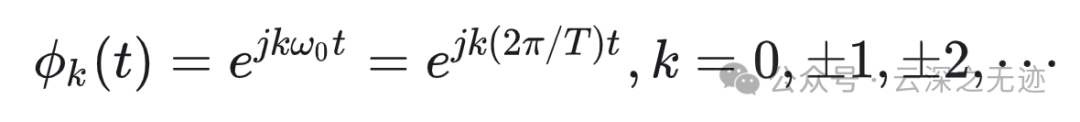
就直接把周期的公式改了一下,代入
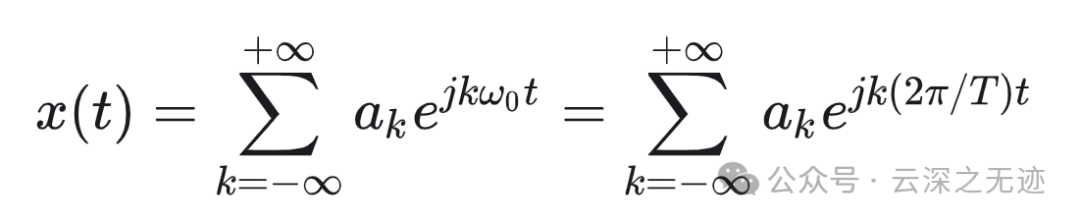
就变成了这样
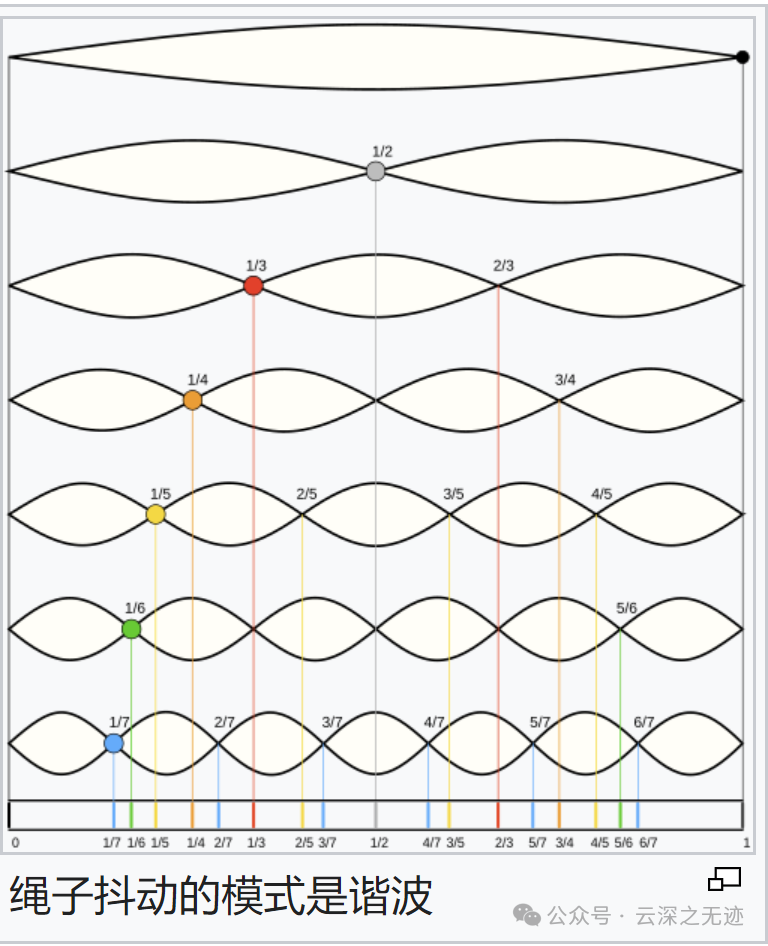
我能做到最好的谐波的图像就这个了。
谐波是一个数学或物理学概念,是指周期函数或周期性的波形中能用常数、与原函数的最小正周期相同的正弦函数和余弦函数的线性组合表达的部分。
傅立叶级数的原理,周期函数都可以展开为常数与一组具有共同周期的正弦函数和余弦函数之和。
其展开式中,常数表达的部分称为直流分量,最小正周期等于原函数的周期的部分称为基波或一次谐波,最小正周期的若干倍等于原函数的周期的部分称为高次谐波。
因此高次谐波的频率必然也等于基波的频率的若干倍,基波频率3倍的波称为三次谐波,基波频率5倍的波称为五次谐波,以此类推。不管几次谐波,他们都是正弦波。
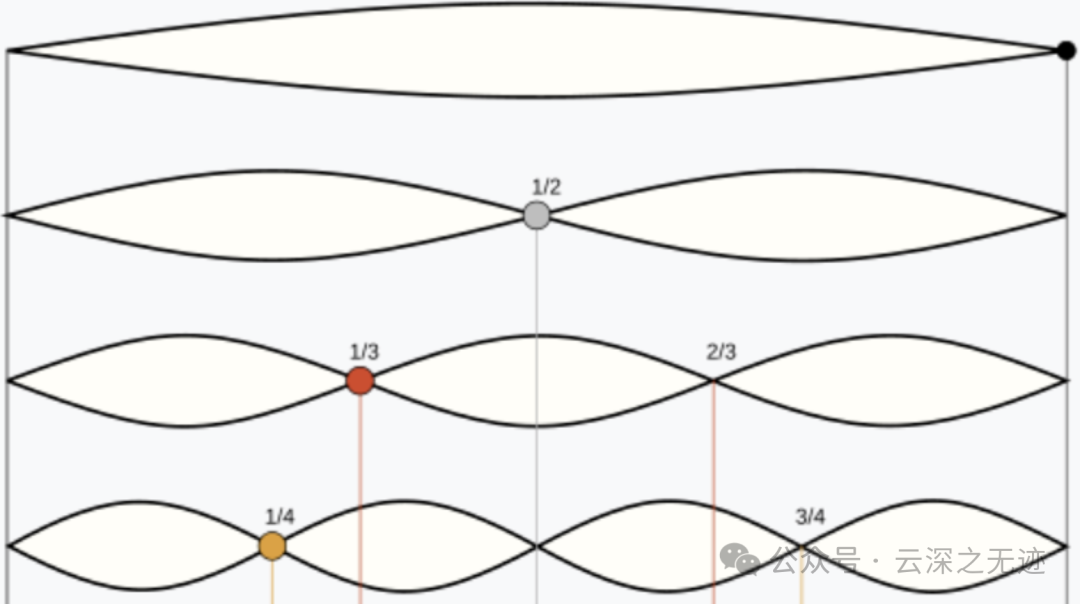
1,2,3,4-无穷也
实周期信号的傅里叶级数
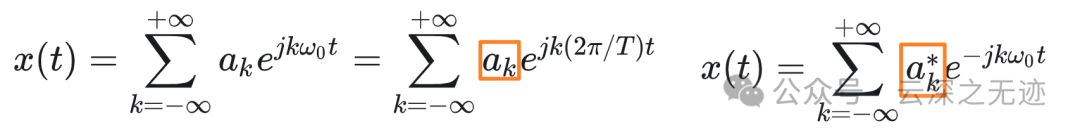
后面就是把前面的式子写成了共轭
以 −𝑘 代替 𝑘 ,则有:
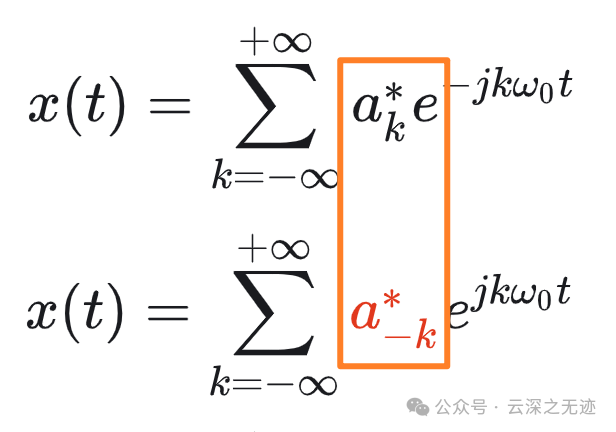
相等
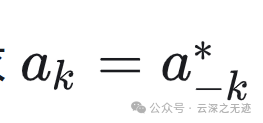
要求这样
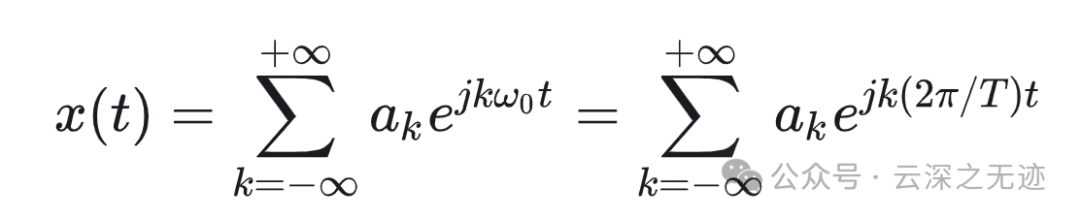
这个时候再对这个公式打开
不知道你能不能看懂其实就是把原本的和共轭的写在了一起,下面的2就是双倍的意思,这种细节不推公式是不容易发现的。

一切都是那么的的顺畅
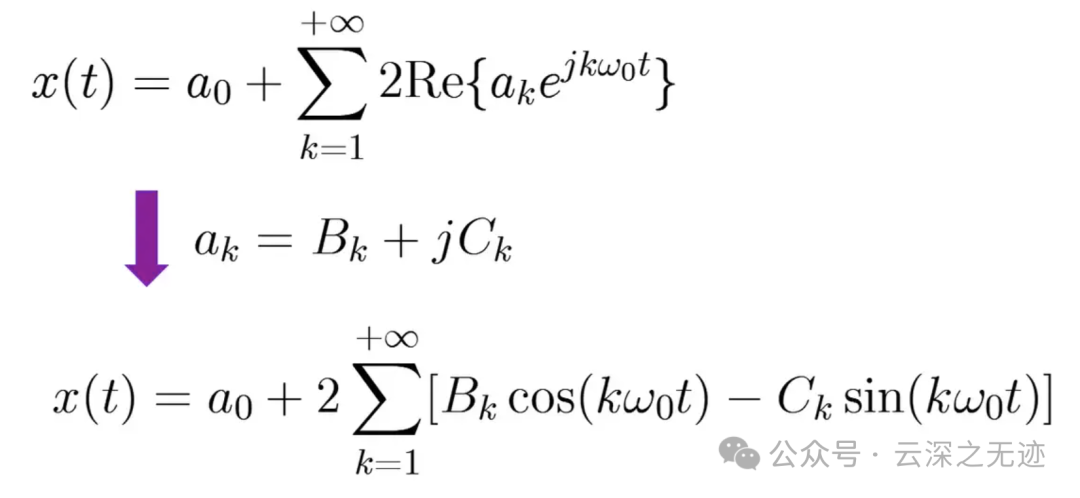
然后我们把改变一种样子,就是三角函数的形式
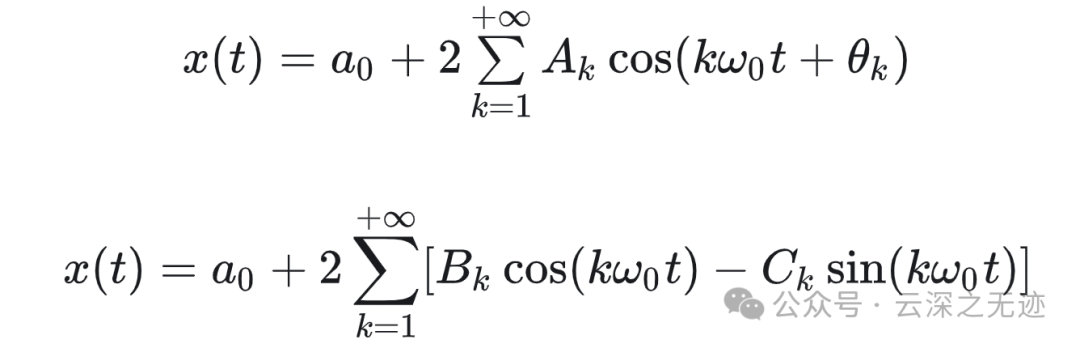
所以实信号下的表示有很多,其实共轭的意思就是构造欧拉公式,因为有俩项e。

直接打开,因为是实信号,肯定是两个e,绘图就是三角函数容易
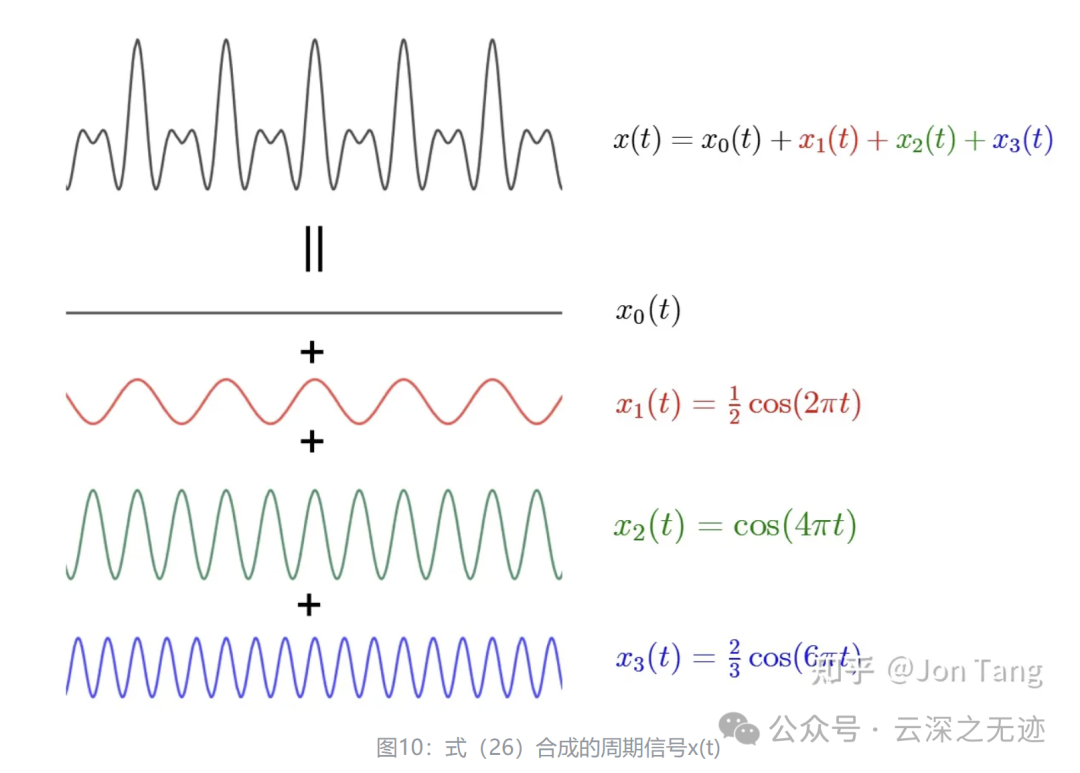
合成的样子,以及也有谐波的样子
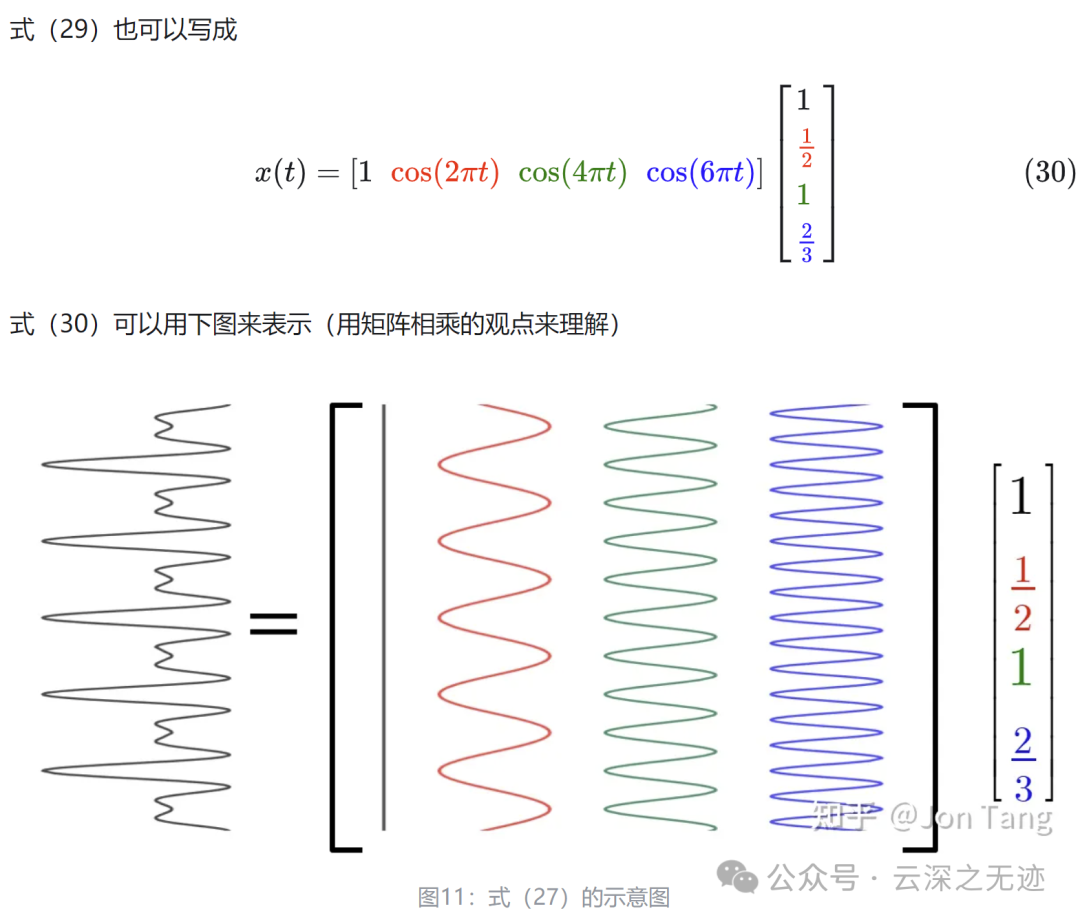
当然也可以线性代数的样子
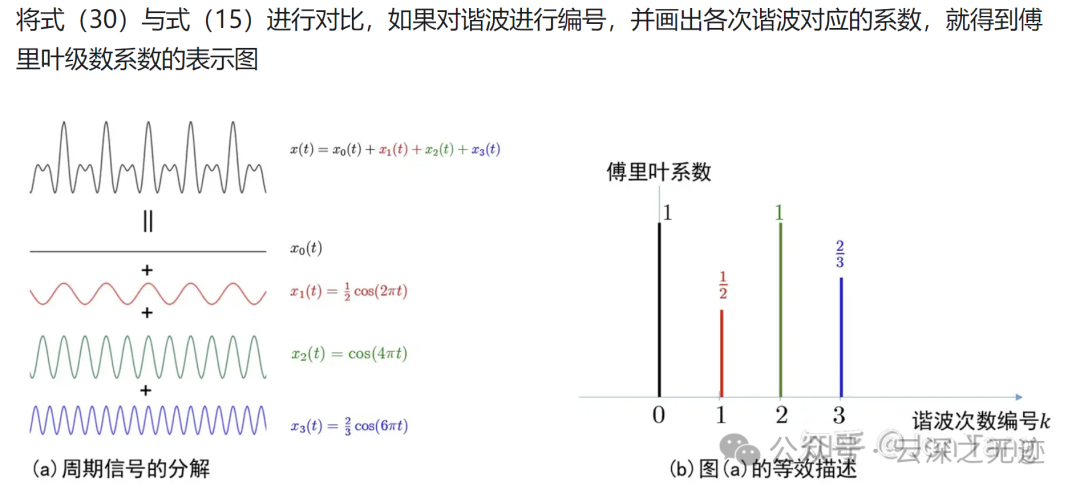
把谐波的次数写出来,不就是把周期信号分解了
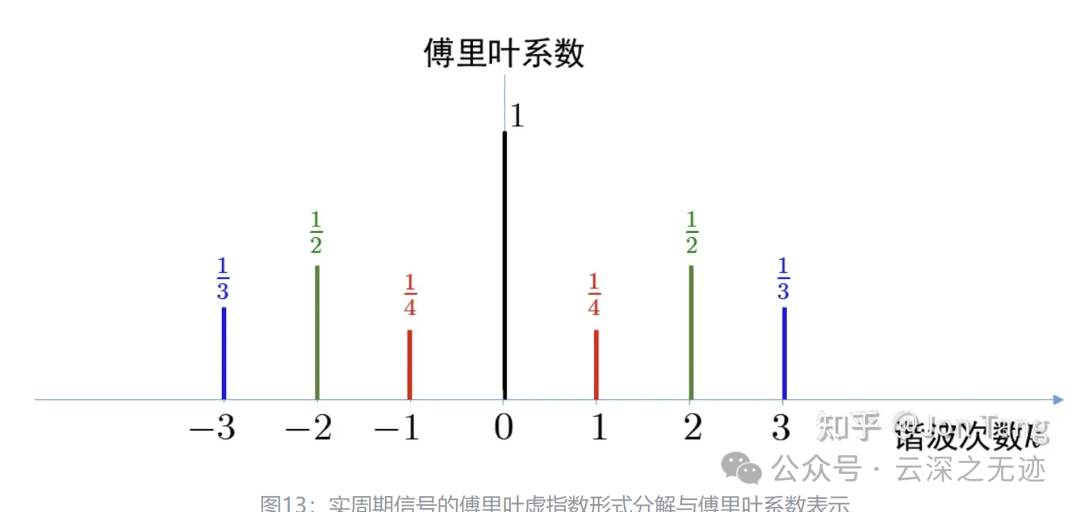
如果是复指数就是两个对称的谱,因为就是共轭的
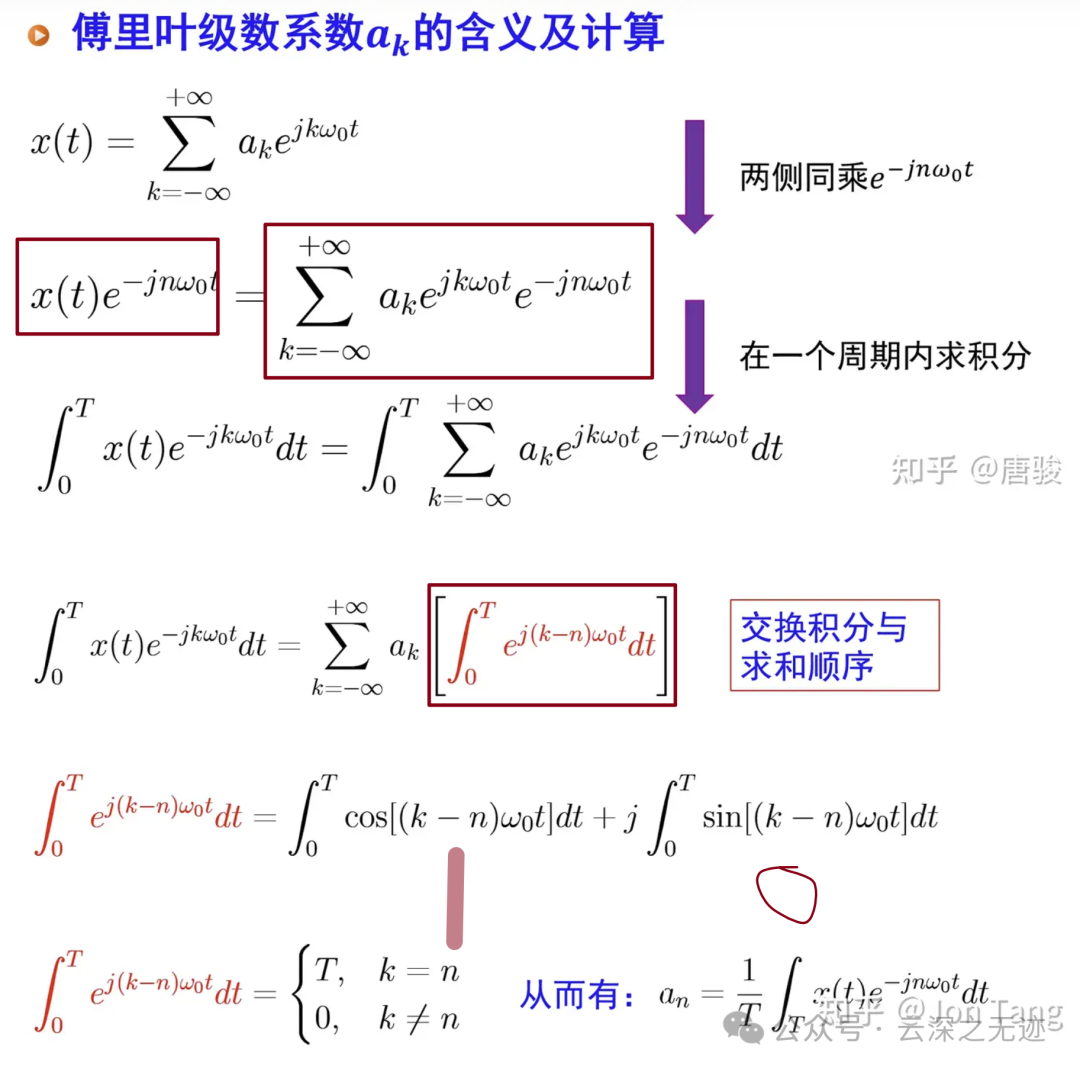
系数的求解是简单的,感受1/T是哪里来的
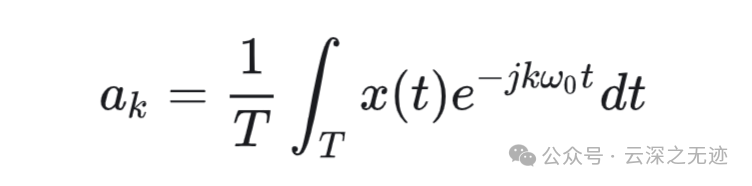
就是这样
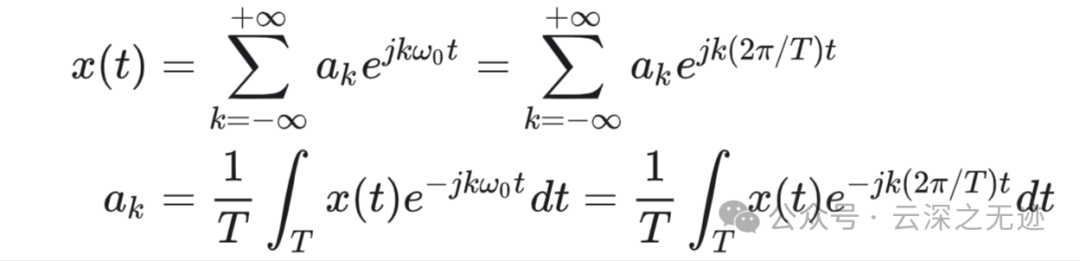
综合是线性组合,分析是求得系数,很自然。
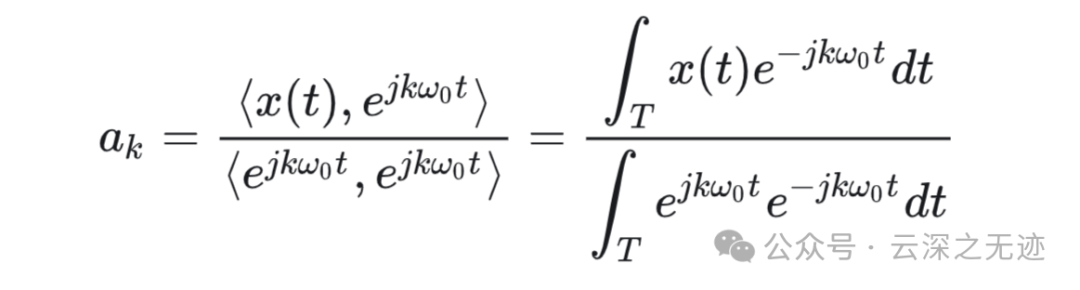
系数其实就是做坐标系里面的单轴值
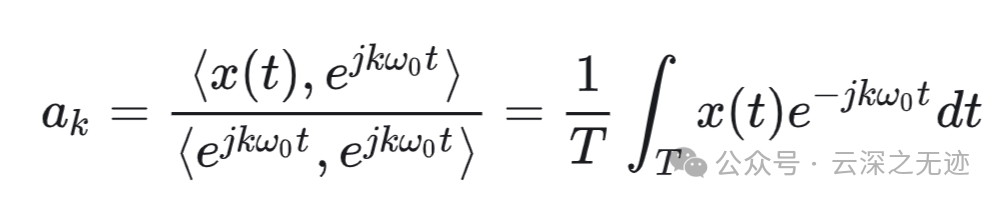
通过内积就可以计算出来
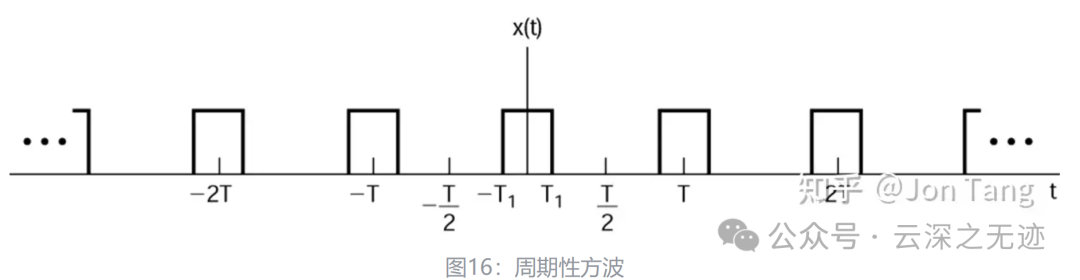
周期性方波是一个永远绕不开的图像:
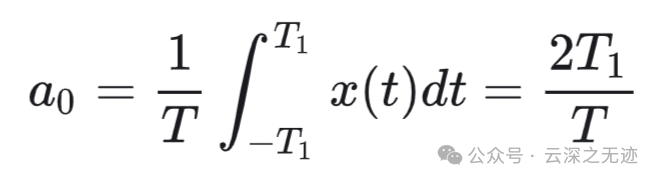
对它求系数
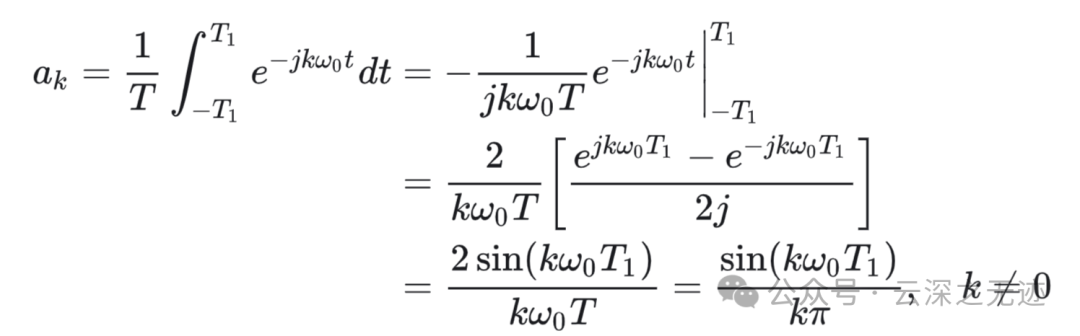
就是这样的结果
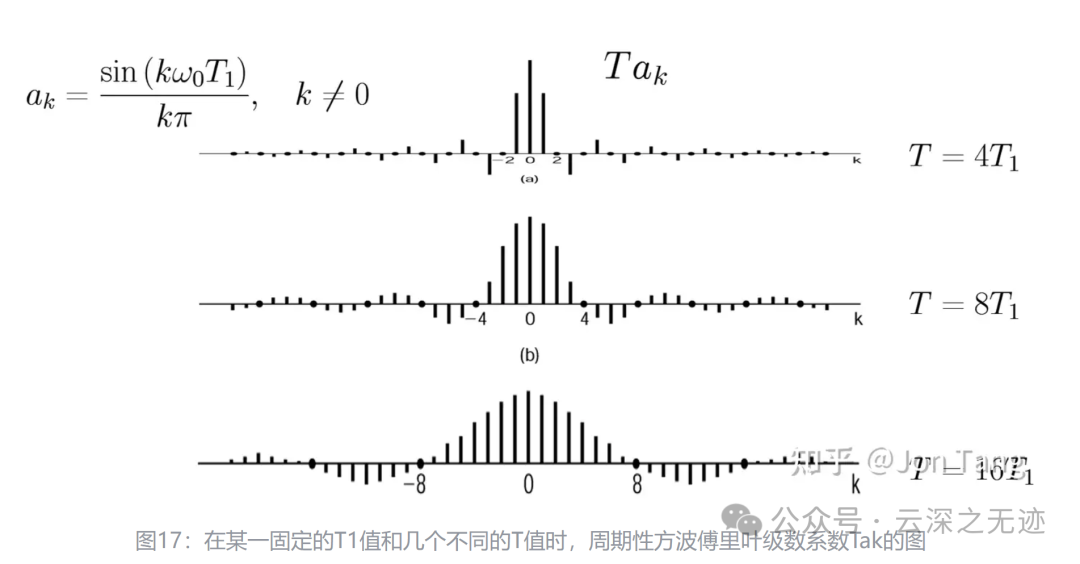
对应在
没忍住把连续也写了。
这里应该是连续和离散都写完的系统部分,不过我觉得可以安排在这里。

卷积最直接地反映了系统的 线性线性 和 时不变性时不变性 。
一个线性时不变系统对一组复指数信号的线性组合的响应具有特别简单的形式。具体而言,在连续时间情况下有:

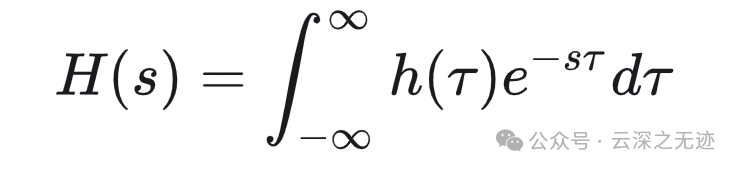
里面的h是冲击响应
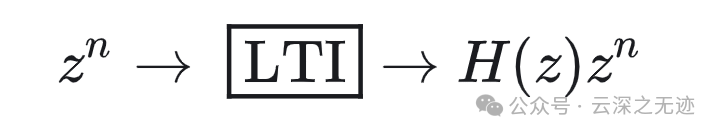
离散而言是这样的,不适应
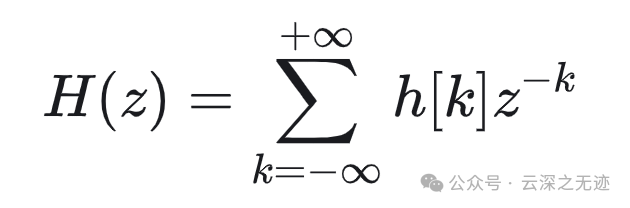
h还是冲激响应

利用系统的频率响应来表示一个线性时不变系统,对 𝑒^𝑗𝜔𝑡 (连续时间)或 𝑒^𝑗𝜔𝑛 (离散时间)这种形式的虚指数信号的响应是特别简单的;而且,由于线性时不变系统具有叠加性质,因此一个线性时不变系统对虚指数信号线性组合的响应也同样简单和容易表示。
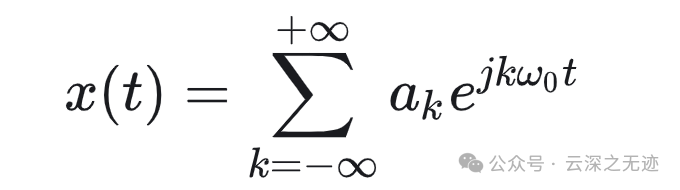
加入一个信号的傅里叶级数在LTI里面
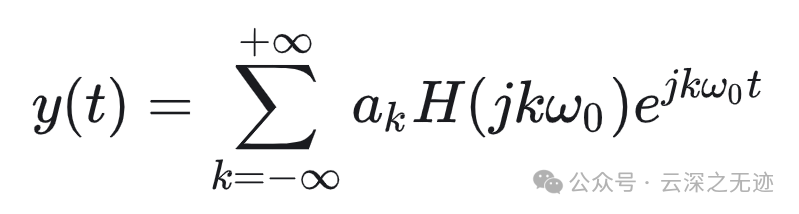
变成这样
线性时不变系统的作用就是通过乘以相应频率点上的频率响应值来逐个改变输入信号的每一个傅里叶系数。

离散和连续,完全就是对偶的,只是离散的需要注意周期

挖坑,有空补
现在是离散时间!!!
线性时不变系统对复指数信号的响应
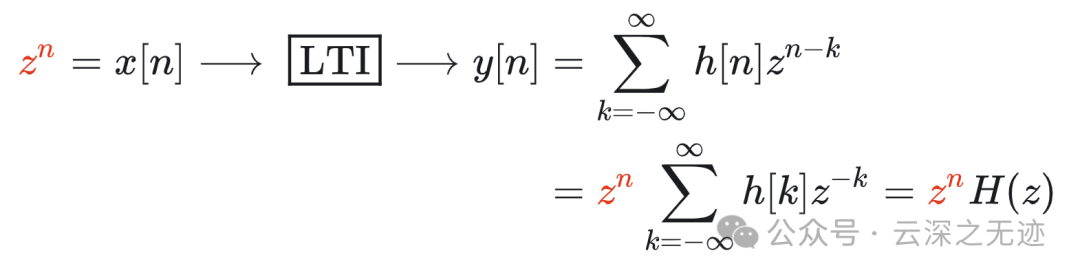
正交的向量一定是线性无关的。什么样的一组信号,既满足相互正交,又恰好是LTI系统的特征函数呢?
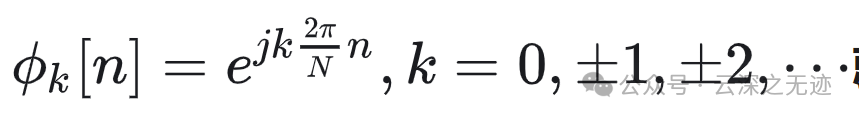
成谐波关系的虚指数序列
成谐波关系的虚指数信号的线性组合,你不疑惑为什么这样做?因为线性组合来表示更为一般的周期序列
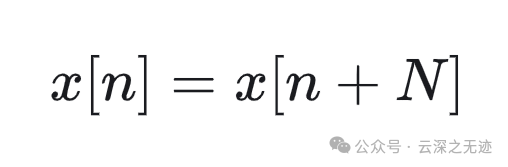
一个周期信号的样子
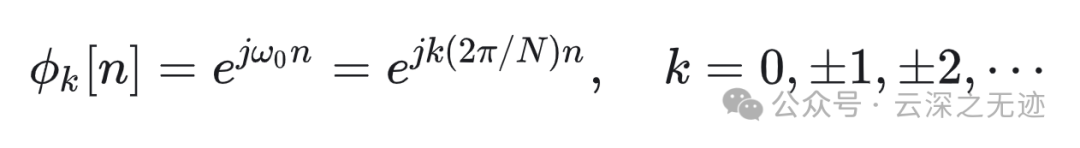
基波都是2Π/N的倍数
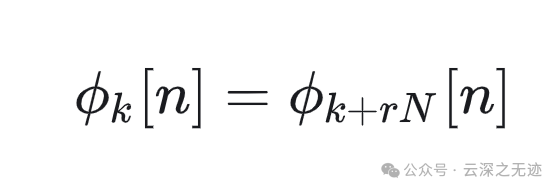
满足这样的序列
那么说回上面,因为谐波正好也是按照整周期出现的,线性组合就有如下形式:
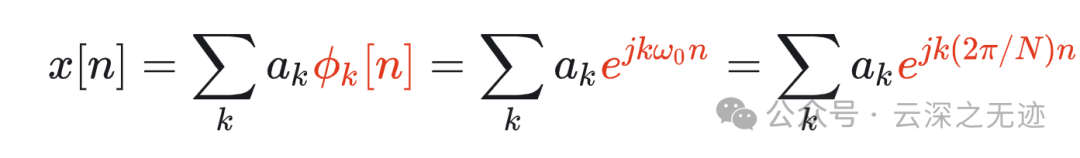
ak是傅里叶级数的系数
这个表达是显然的,因为离散的序列我们就是要N个相继的整数。标有红色的意思是有着不一样的表达方式。
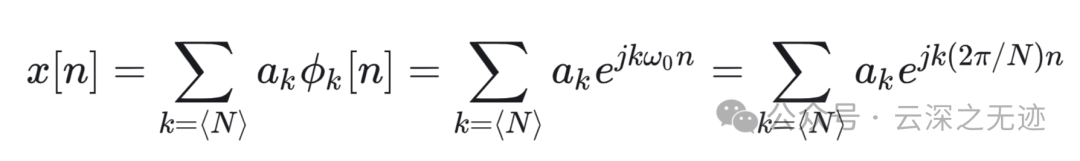
下标的变化是说明,k是一个变量,指代,N是连续变化的区间
以上也称离散时间傅里叶级数。
周期信号傅里叶级数表示的确定
级数的难点也在求系数,可以解线性方程组,也可以使用和连续一样的做法,使用内积来求解。
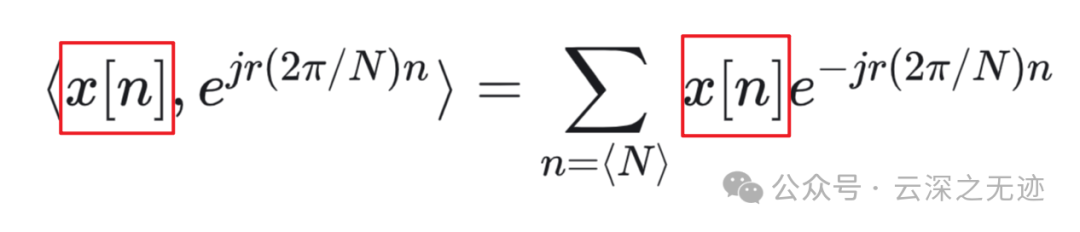
这里的r是一个整数变量,对这两个东西求内积
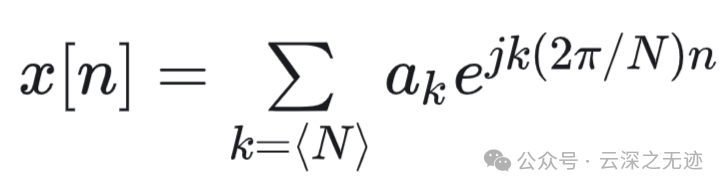
将上面的线性组合代入内积
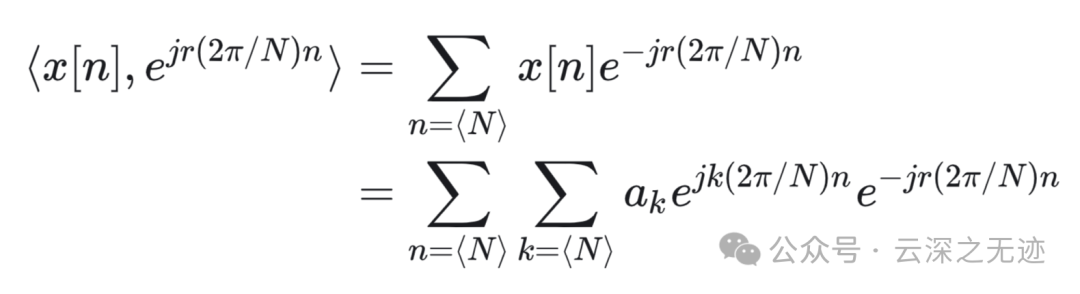
得到这个
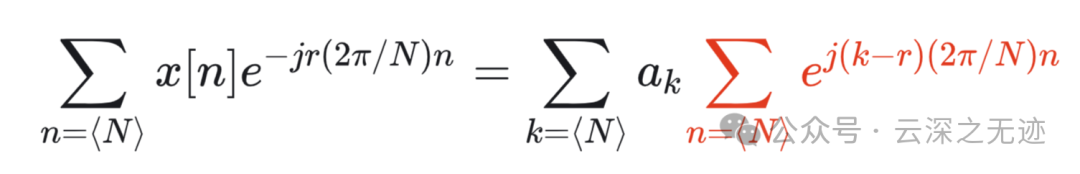
把右边的求和顺序改变,这样就把系数单独的摘出来了
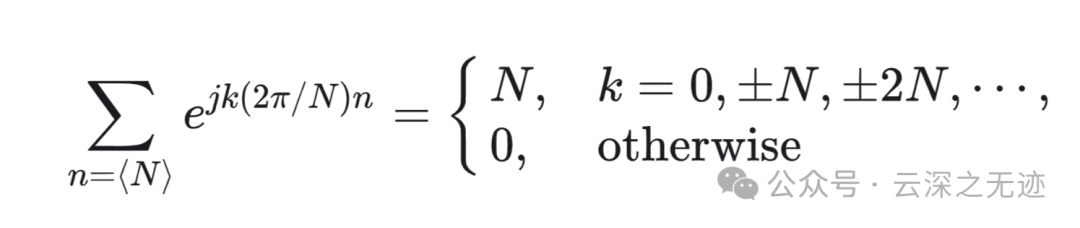
利用这个正交的结果
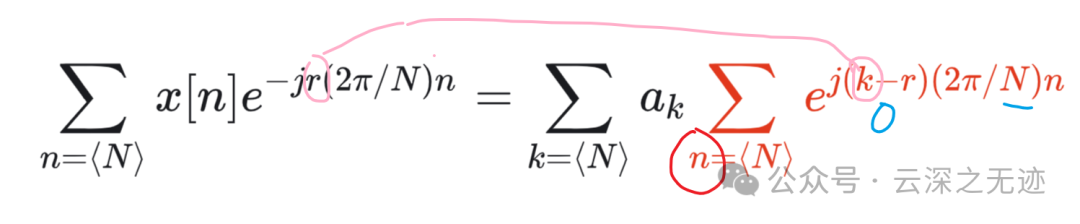
这点应该是最难的

这一段讲的是如何处理有段,两个求和式。其实按照内积的算法来看:
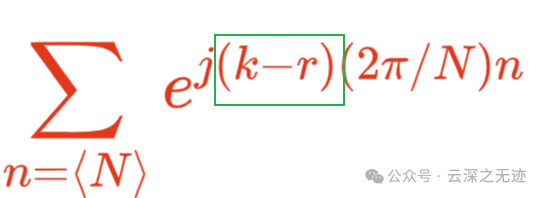
k-r这一项是多出来的
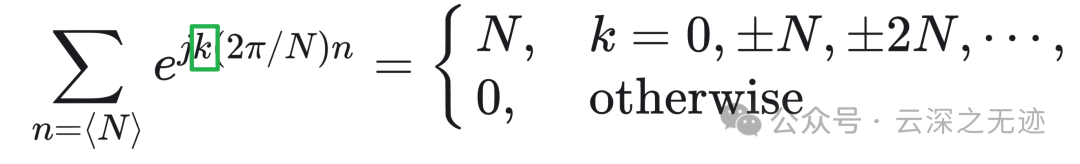
就是这一项,括号里面的项是和两个数有关系的
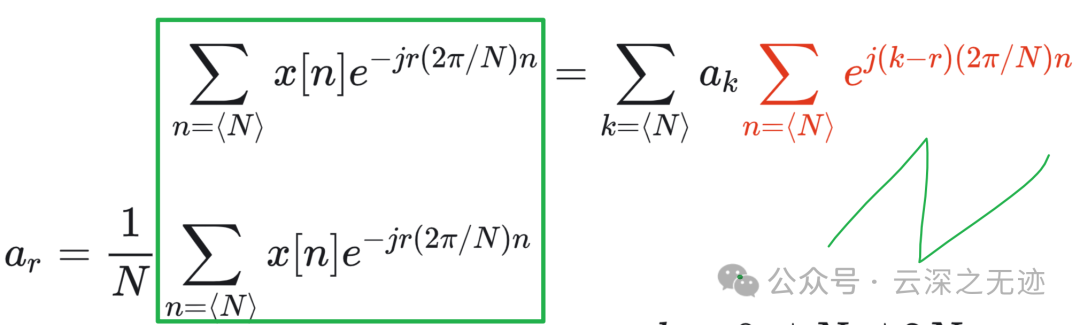
最下面的参数就是系数了
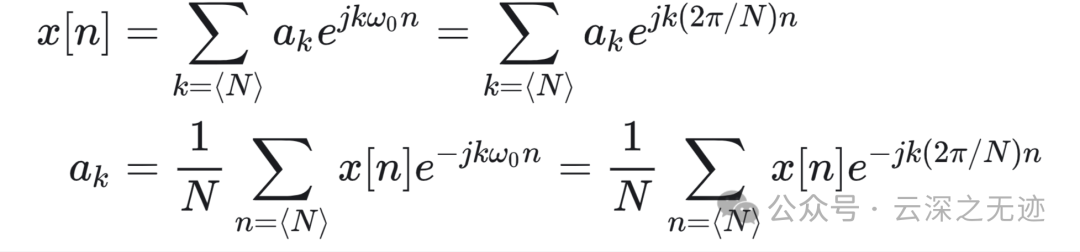
对偶的同样可以给出离散傅里叶级数对
这段里面,我们单纯看公式是可以得出,我们只需要N项就可以完成拟合的工作。其实不然,我们再看一次线性组合:
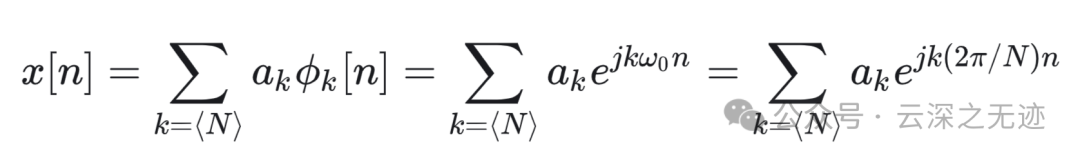
这个.11
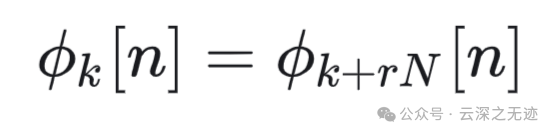
以及这个

其实我没有完全搞明白它说的意思:
假设考虑的 𝑘 值多于 𝑁 个,那么 𝑎𝑘 的值必定以 𝑁 为周期,周期性重复。这个性质特别重要!
因为只有 𝑁 个不同的虚指数(周期均为 𝑁 ),所以离散时间傅里叶级数表示式就是一个 𝑁 项的有限级数。
大概就是说,这个线性表示和系数的对偶性,因为都是呈周期变化的。
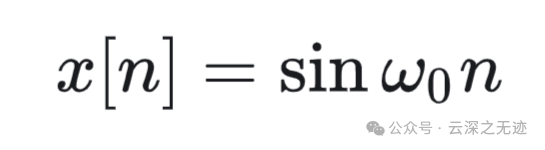
离散最重要的就是周期了

𝑥[𝑛] 是周期的,其基波周期为 𝑁 ,这时所得到的结果与连续时间情况下的结果完全类似。把信号展开为两个虚指数信号之和,可得:
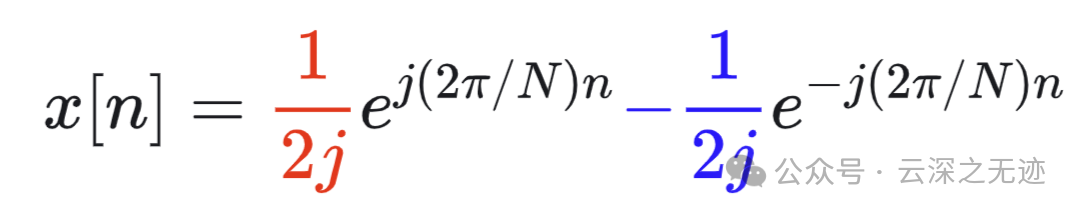
就是把w带进去,然后欧拉公式打开
而在一个长度为 𝑁 的周期内,其余系数均为 0 。
这些系数以 𝑁 为周期重复,所以aw+1=1/2j,aw-1=-1/2j,这个就是两个参数,一个负的,一个正的。
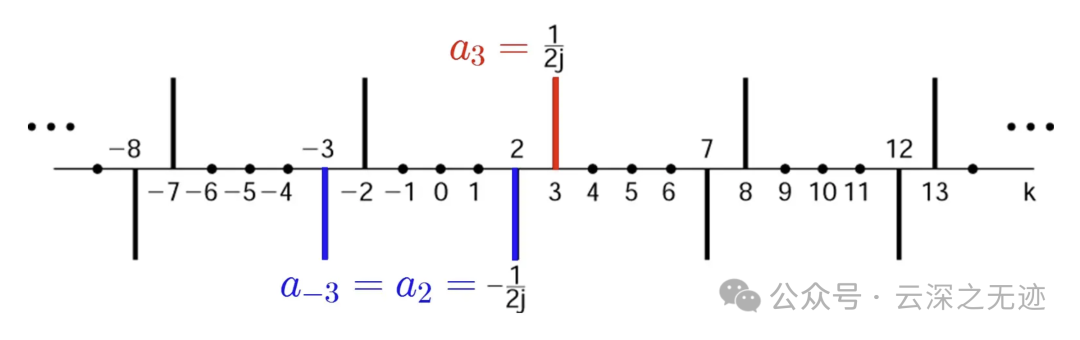
对于这个例子,N=5时,其傅里叶级数的系数示于图中。
图中指出,这些系数是周期性重复的。然而,在综合公式中仅仅用到其中一个周期内的系数。
说了这么多,就是展示系数是周期出现的。
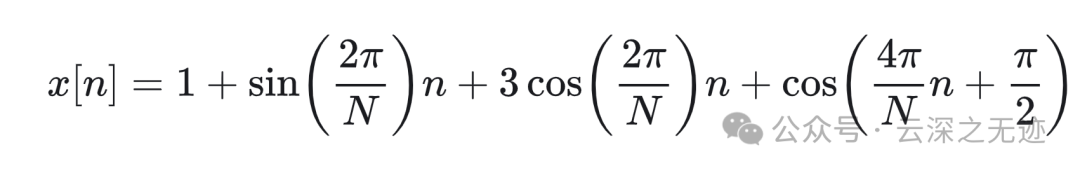
这个也是,展开合并

就是这样

系数
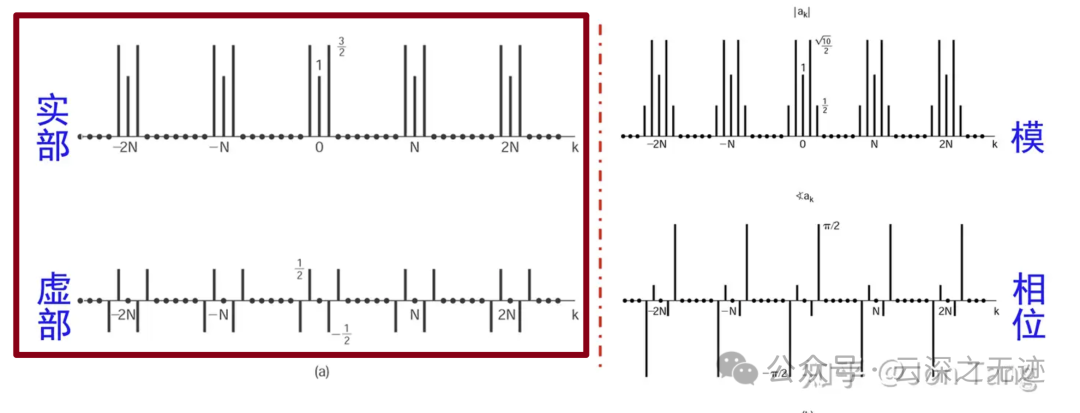
在一个图里面画出系数

还有离散周期方波序列
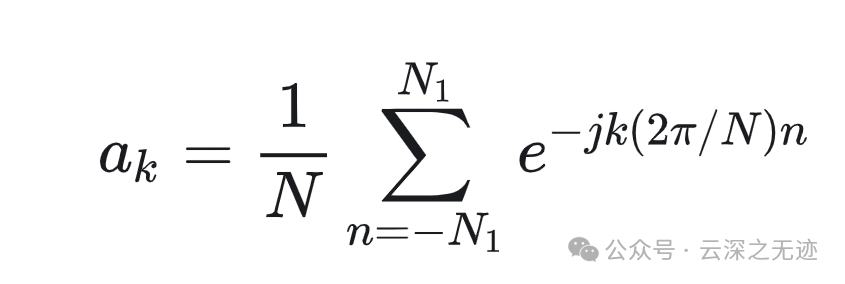
取一个周期
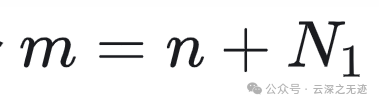
m是一个拓展的周期
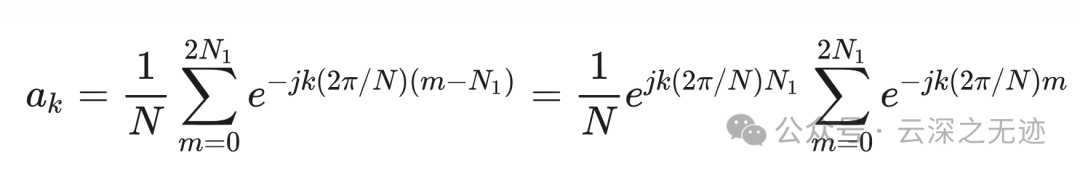
这就是变成了一个几何级数的前2N+1项的和
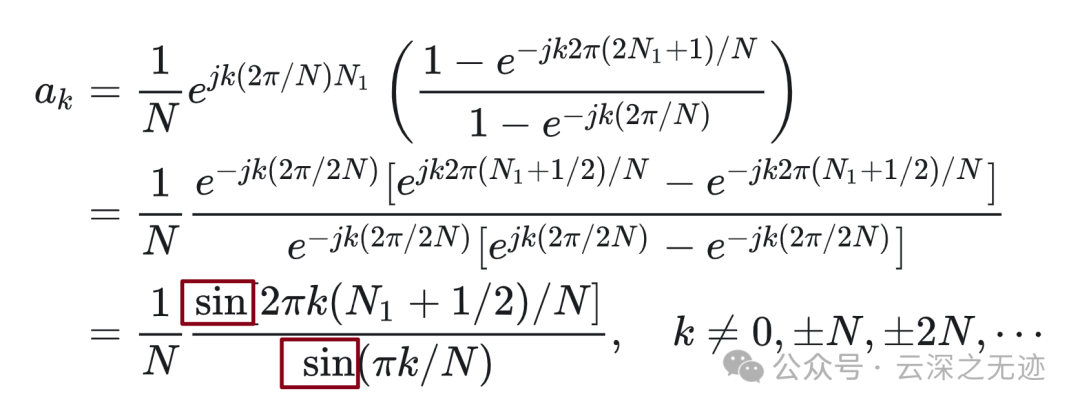
就看这里最后的结果形式
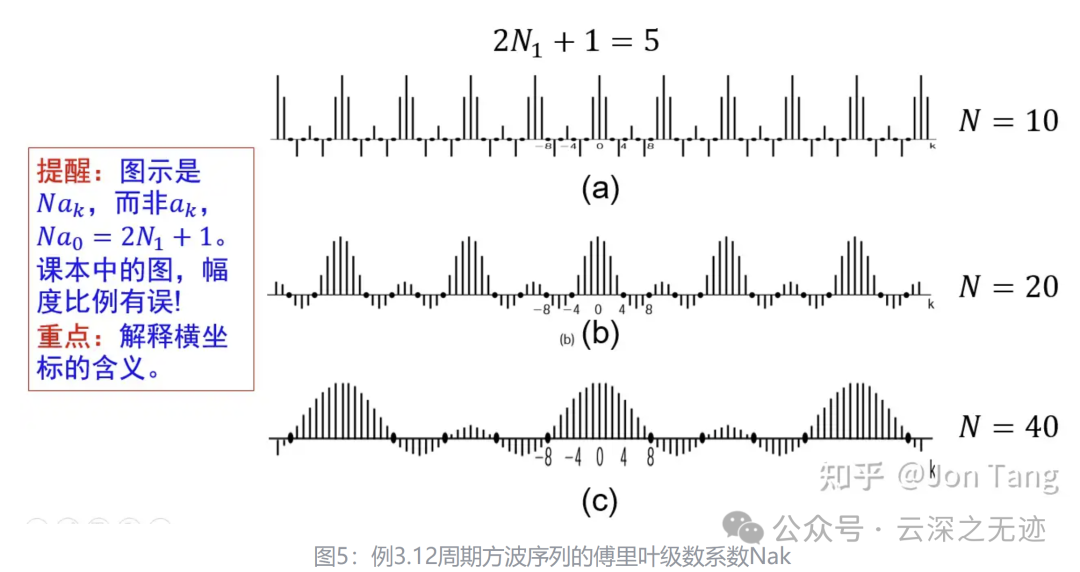
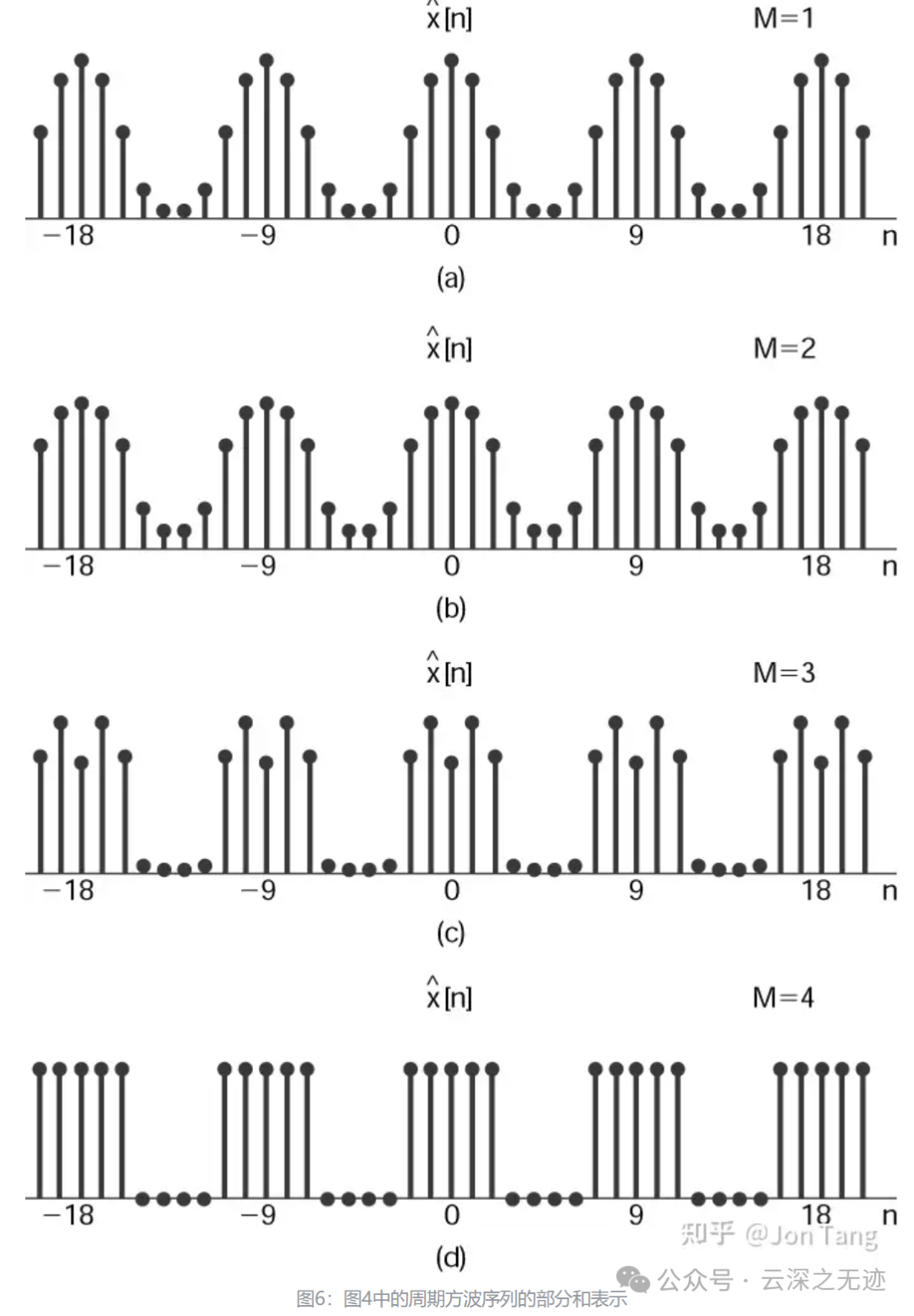
可见,与连续时间情况相比,这里不存在任何收敛问题,也没有吉伯斯现象。事实上,一般来讲离散时间傅里叶级数不存在任何收敛问题。究其原因,依赖于这样一个事实:任何离散时间周期序列 𝑥[𝑛] 完全是由有限个参数(即 𝑁 个)来表征的,这就是在一个周期内的 𝑁 个序列值。
傅里叶级数分析公式只是把这 𝑁 个参数变换为一组等效的 𝑁 个傅里叶系数值;而综合公式则告诉我们如何利用一个有限项级数来恢复原来的序列值。
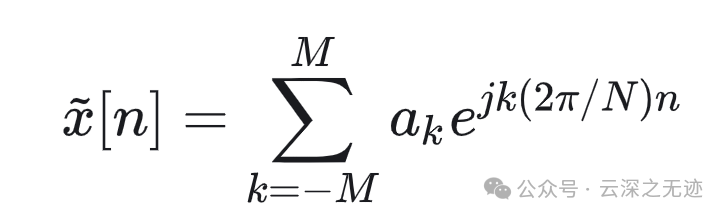
因此,若 𝑁 为奇数,而我们取 𝑀=(𝑁−1)/2 ,那么上式中的和就完全包括了 𝑁 项,于是由综合公式就能得到 𝑥~[𝑛]=𝑥[𝑛] 。
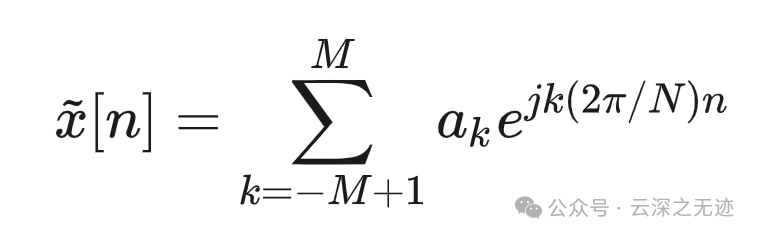
偶数的结果也是一样的
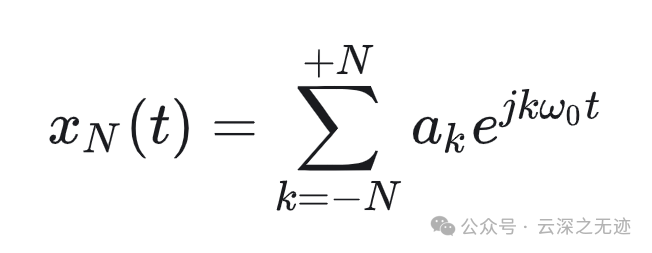
预告一个2000
