不是原创，就是把我学习中帮助理解的东西集合在一起，我觉得这个东西我不写出来，绝对不会有人向我这样扣的细的。记录也好，复习也罢。
先说为什么我们会这个响应念念不忘？
在特定的时空中研究具体的系统，如果时空是静止的，这个世界将很难想象，所以，系统的状态通常都是时空的函数，即随着时间、空间而变化，而研究自变量和因变量变化关系的数学工具正是导数，各变量导数之间的关系受自然规律约束，即形成微分方程。所以，微分方程就概括了系统的全部，就是系统的数学结构，解出来就知道系统对外部的信号如何响应的。
这里需要补充很多文章中出现的概念：
“初始松弛”十分形象、十分贴切，比如你要研究一个弹簧拉伸长度与受力之间的关系，通常而言，如果外力为零，弹簧就应该处于松弛的状态。
也就是系统放在哪里，没干扰的情况。
线性常系数微分方程和线性常系数差分方程往往只是输入-输出的一种约束关系，而非显式函数表示
离散时间系统的单位脉冲响应分为有限长和无限长，对应的系统分别称为FIR系统和IIR系统。
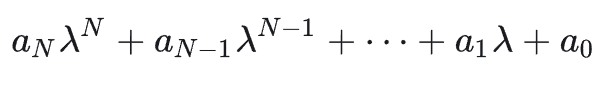系统的特征多项式
这个式子等于0 的时候是特征方程，里面解出来叫系统的特征根。
然后就可以表示0输入响应为：
很明显也是特征根的线性组合
模式是有e，也就是指数函数的，上面的参数才是特征根
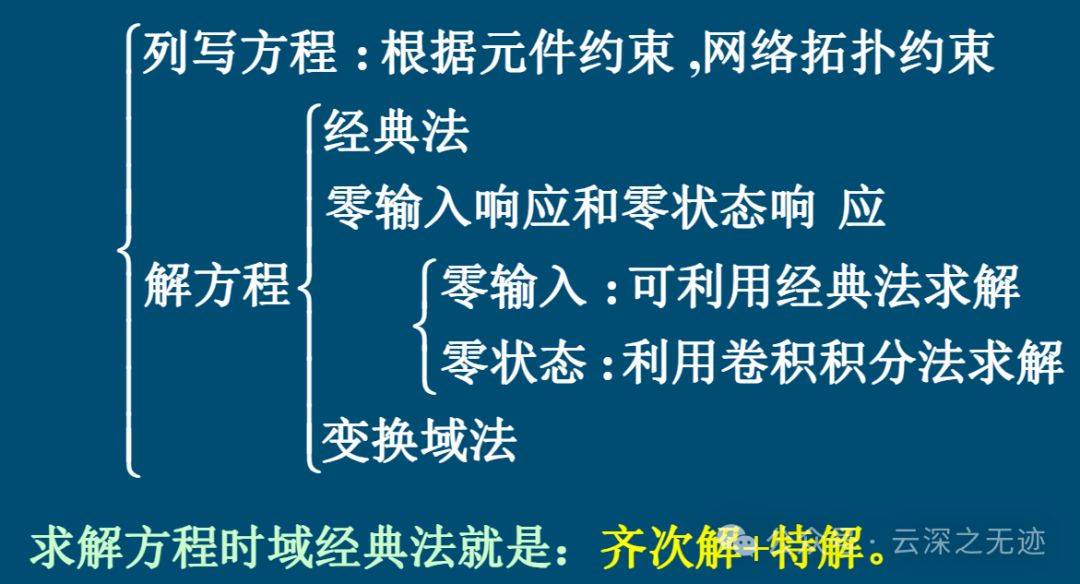
第一步写的真装逼，其次文章里面我没有写变换域，后面会有的。
两个约束
无非就是CLR元件，就这样就写出来了
经典法很固定，谁也可以算出来，后面的激励是固定的两种才可以求解
这个就更清晰啦
一般就是解出来是这样的
这种经典时域法也叫强迫响应，因为是x(t)位置，然后就是后面的激励是幂函数和指数函数，只有唐老师说明白了为什么这样的方程可以解出来。
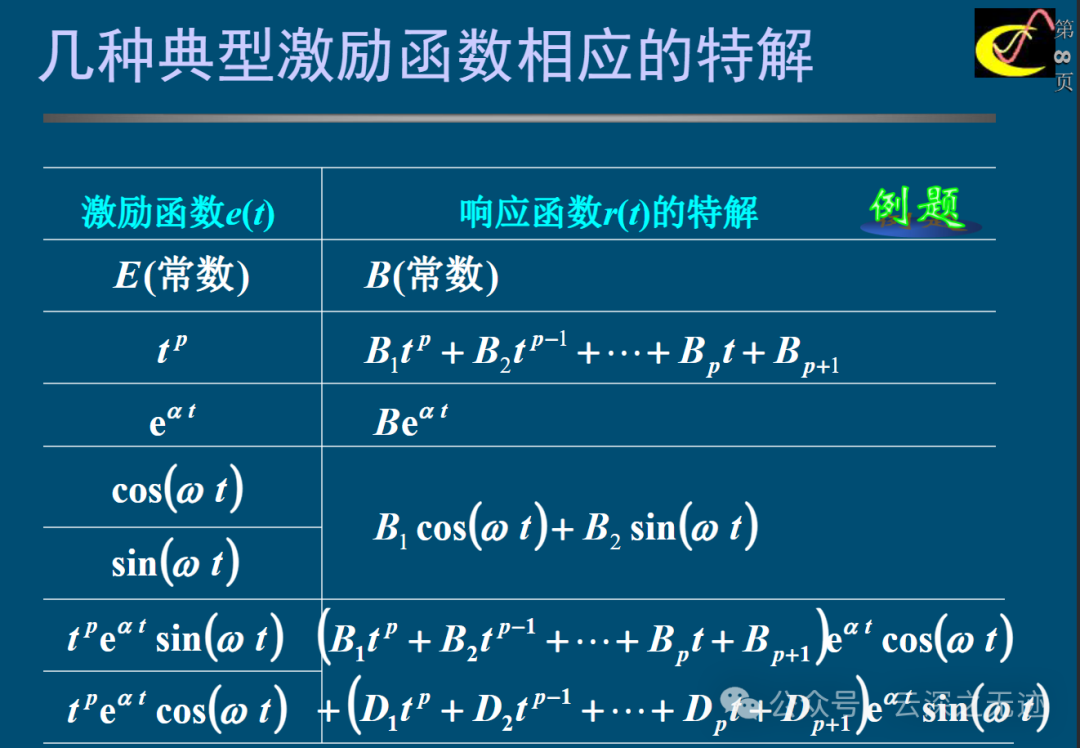
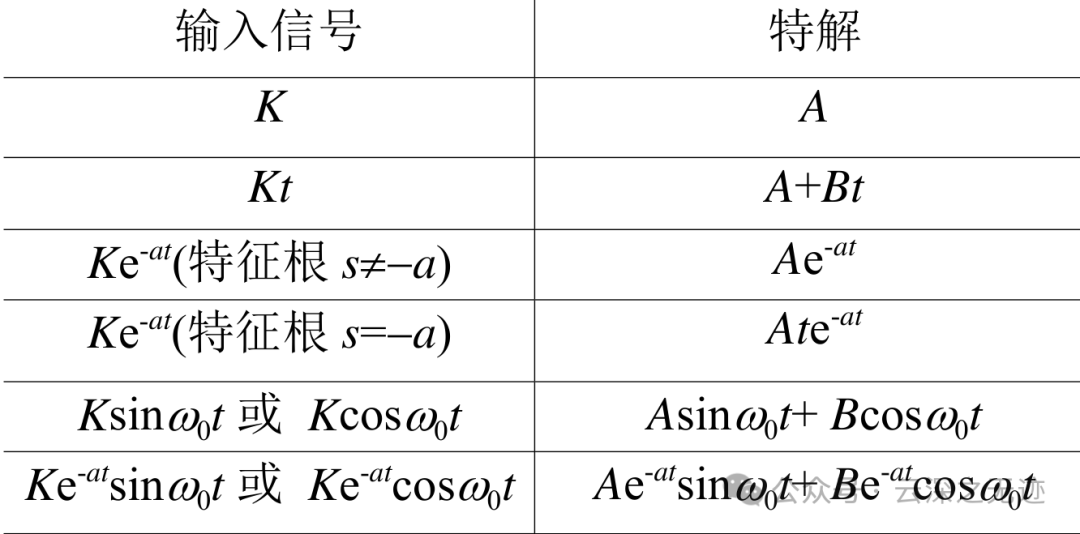
以上都叫受迫响应，下面是唐老师的
可以看到图表里面有1，2他们的形式一样
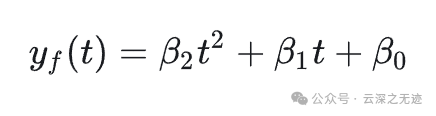
受迫响应，里面是没有指数函数的项的，就是上面图里面的不含有特征模式
这PPT有问题哇，写错了
所以设置成这样的特解
就是这样的
因为是2阶系统，所以有两个约束，也就是0和导数0
因为经典的时域办法只能处理
这样的激励项，如果这个信号变化，后面就是要重新的计算，如果初始值也变化，也就是后面的解方程也是需要在计算的，最后这就是纯纯的数学办法，不是很好回答物理上面的直观解答。
其次，得到的是完全响应，而无法分解为由内部条件和外部条件分别引起的分量。
我觉得经典时域法应该是差不多就这样了，接下来就完成卷积法。这个想法其实非常的自然，我们的难点就是求这个外部信号带给系统的响应，我们自然想用前面的东西，卷积正好就是，使用系统的响应和激励一卷积就求出来ZS状态的响应。
卷积法
不管是什么方法，我们都是要找到0输入和0状态两个解，然后加起来就行。因为0输入是系统蕴含的特性，所以可以使用经典时域法里面的求齐次方程解的办法。
也就是这个PPT里面说的内容
这个前部分简单
一般解出来的就是这几个结果，高数书也是这样写的
难得是这个0-的部分
你觉得这个0-，是什么东西，它在0之前就有，所以是：系统对内部条件的响应，零输入响应
题里面说的就是这样的情况，就是在信号来之前，我们对系统的状态是知道的，也就是0-，初始条件。
我们来好好的理解一下这段话的核心内涵，首先要时刻知道一点，系统现在的响应的能量来自于哪里？
看第一个，如果是t=0输入的，0-的时候，肯定就是没有外部的能量干扰，然后0+的时候能量有了，外部输入就起作用了。
第二个是，一般我们指0-是初始条件，因为这结合第一个说就是，0-的时候其实就是系统原有的响应（也可以说能量，但是就方便理解，可能不多说的），也就是说题里面给的0-，是初始值的意思。
第三个，如果这个系统没有外部能量输入，那这个0-，0+是一样的，因为在0+，系统没有变化。
最后一个，全响应是有俩项的，最后激励的加入是导致0+以后系统的充能的。
所以记住一点，全响应的时候是不同的，还要知道他们两者之间的独立性
此时看题，就很明白了，要的是0输入，ZI，那初始值就是这样，直接计算就好了。
ZI的值，后面一项是为0的，所以就没有用，即使难也没有用到
这个是复根的，一共三个，完美了，全网最佳的文章出现了
接下来是ZS的求解
叽叽歪歪说了这么多的意思就是：
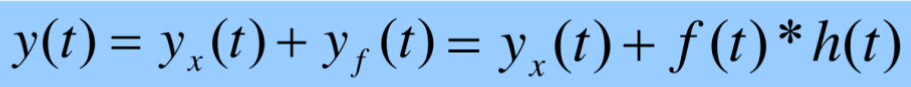
可以把后面的激励项和系统的响应做卷积
直接 推导好不好
先不说里面的算法，反正就是这样的纯联系，都给你了，不卷积等什么
还记得我上篇写的东西吗？
后面的函数就是脉冲信号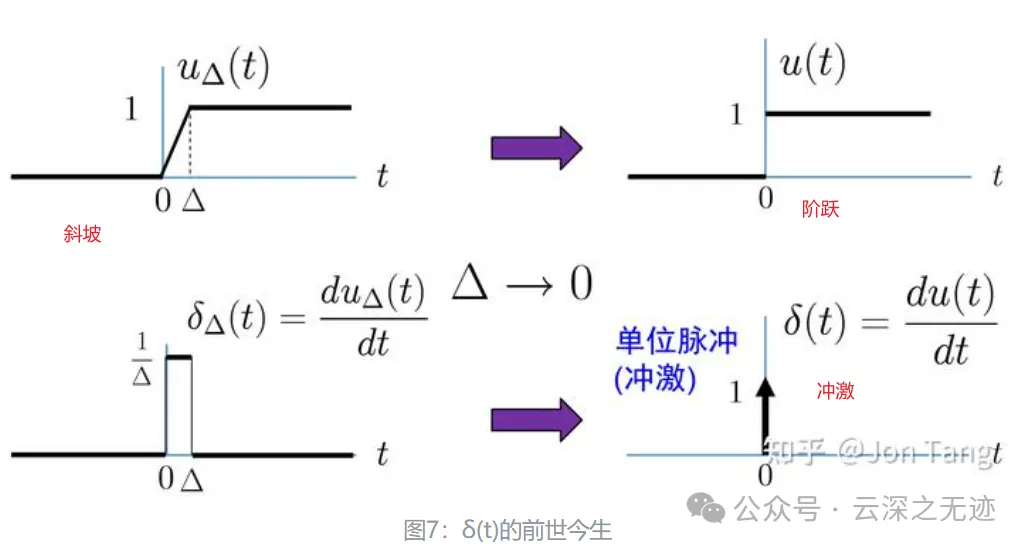
最后一个，单位的冲激信号
信号与系统漫谈-基础回顾
这个是PPT的写法，这就是教科书，你得感悟多久？知识还是没把握住
唐老师的内容分为两个部分
第一部分是对微分方程求解参数形式的限定，后者是解释了脉冲对系统的影响。第二句话很重要，是写单位脉冲的响应其实是在0-的时刻，也就是说已经影响到了0输入的值，这样就可以保证所有的初始状态都是0的情况下开始注入冲击。
但是就很快，就在0的时候搞一下，活好不粘人。接着就是系统开始消化这能量，开始响应，所以就是又开始有了系统的特征模式的组合。
这个是2.17 - 线性常系数微分方程
第一个式子很简单，就是要考虑=0的时候系统里面的事情。接着就是求解方程了，x是一个连续时间的冲击信号，f是响应，最高次的系数也简单，前面是求和符号，肯定最高就是几次求和，右边也一样，要想左右一样，肯定是系数就一样的。右边就是冲击信号的系数，也就是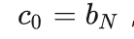
。
也就是说明了，最后响应式子里面冲击信号的系数是可以通过这样前后匹配的方式求得，我觉得我讲明白了，不知道你有没有看明白，这可是最难的东西了。
这是是n＞m，直接就是一个特征值的线性组合了
一开始PPT下面还有一个n≤m，要平衡就要多一个冲击的导数，和后面一约，就变成上面的了，这就是加一项的处理方法，其实就是个数学的恒等式，简单的咧。
判断，题要什么，是冲击响应，然后就是f和y换成响应和冲击，接着是求解方程，判断m和n的关系，代入原方程，求解。
n和m其实是N，M就是最高项的阶数，平衡状态是一一对应的
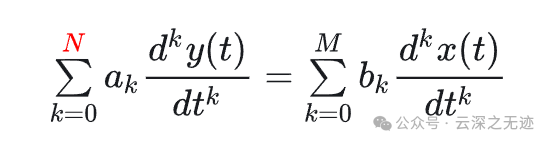
唐老师讲了这两个MN系数之间的关系和取法。
说明了系统的作用，以及MN参数对系统的影响。
再一次说了，0输入响应，就是系统自身蕴藏的能量，与外界无关。
0状态是所有都为0，就是内部的状态也是0，这个时候输入一个能量来响应。
太晚了，脑子不转了。
