第三代半导体GaN基材料与蓝光激光器发光原理,能带计算
一:GaN基材料与激光器
GaN 基材料一般是指氮化镓(GaN)、氮化铝(AIN)、氮化铟(InN)以及其多元化合物(如 AIGaN、InGaN、AIInN、AlInGaN)。相较于第一代半导体 Si、Ge与第二代半导体 GaAs、InP,GaN 基材料因其具有禁带宽度大、直接带隙、强极化效应(Polarization)、电子饱和迁移速度大等特点,在光电、电力电子以及微波射频领域有着广泛的用途,因此也被称作第三代半导体。
通过对GaN及其多元合金A1GaN,AIGalnN组分的调节,可以得到0.64~6.2eV连续可调的带隙,理论上可以实现从红外到深紫外波段的发光。
带隙与波长的关系
带隙能量(Eg)与光的波长(λ)之间的关系可以通过公式来表示:
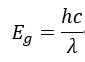
其中:h是普朗克常数(6.626×10−34 Js), c 是光速,λ 是波长。对于纯氮化镓(GaN):
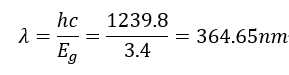
这意味着纯氮化镓的带隙对应于紫外光谱区域的约365纳米的波长。
合金的影响
通过调整氮化镓合金(如AlGaN或InGaN)中的成分,可以改变带隙大小,从而改变发射光的波长。例如:
· AlGaN合金的带隙大于GaN,可以覆盖从紫外到蓝光的波段。
· InGaN合金的带隙小于GaN,可以覆盖从蓝光到绿光甚至近红外的波段。
实际应用
在实际应用中,通过调节合金成分,可以制造出发射不同波长的激光器。例如:
· GaN 基的激光二极管通常用于产生紫外线或蓝色光(约350nm至480nm)。
· InGaN 基的激光二极管可以用于产生绿色或黄色光(约500nm至580nm)。
总之,氮化镓及其合金的带隙能量决定了它们可以发射的激光波段。通过调整材料成分,可以覆盖从紫外到近红外的广泛波长范围。这些特性使得氮化镓成为现代光学器件的重要材料。
1995年,Nichia公司利用双流金属有机化合物化学气相沉积方法,在蓝宝石的C面(0001)衬底上进行生长,如图1所示,其使用增益波导结构,得到了阈值电流为1.7 A,阈值电压为34 V,激射电流密度为4 kA/cm2,激射波长范围为410~417 nm的GaN基紫光激光器,使GaN基激光器得到了零的突破。
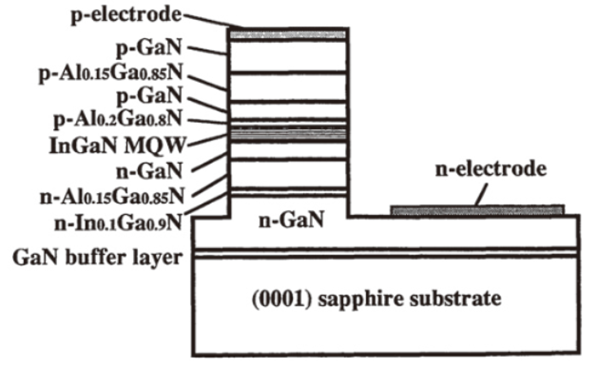
图1 Structure of the first InGaN MQW structure LDs.
二:GaN 激光器发光原理
典型的GaN基激光器的结构示意如图2,在z方向从下到上依次为n电极、GaN衬底、n型A1GaN下限制层、n型hGaN下波导层、多量子阱(MQW)有源区、非故意掺杂hGaN上波导层、p型电子阻挡层(EBL)、p型A1GaN上限制层、p型GaN层以及p电极。
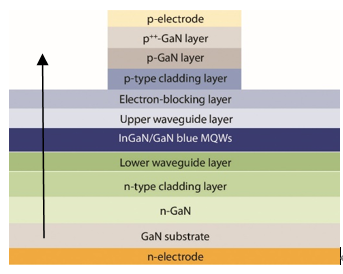
多量子阱有源区(MQWs)的材料折射率最高,且有源区两侧材料的折射率呈现递减的趋势。通过z方向材料折射率中间高、上下低的分布,可以将z方向的光场限制在上、下波导层之间。在y方向,激光器两侧的部分p型层通过刻蚀去除,并沉积了二氧化硅(Si02)薄层,最终形成了一种脊型结构。二氧化硅和空气的折射率要小于p型层的折射率,因而y方向的折射率呈现中间高、两侧低的分布,光场被限制在脊型中间。由于y方向、z方向对光场的限制作用,yz平面内的光场呈现椭圆形分布。在x方向,通过机械解理或者刻蚀的方法可以形成前、后腔面,且前、后腔面的反射率可以通过蒸镀介质膜来进行调控。通常前腔面的反射率要小于后腔面,以保证激光从前腔面出射。
为了保证电流注入的载流子集中于有源区,以提升有区域的载流子密度与光增益,所谓有源区就指的是载流子在此辐射发光的光源。作为有源区的量子阱位于中央,p型和n型的禁带宽度都比有源区大,这样在通过p型和n型材料分别注入空穴和电子后,载流子可以被限制在有源区。此外,在进行激光器的加工工艺时,通常会在一侧刻蚀出脊形结构然后在脊形两侧沉积介质薄膜(Si02)。这样在注入空穴时只会注入脊形以下的区域,在横向也形成了限制。
三:GaN 激光器的能带
InGaN(铟氮化镓)量子阱的带隙计算涉及到多个因素,包括材料的成分、应变效应、量子限域效应等。InGaN量子阱的带隙计算需要考虑合金组成依赖性、量子限域效应以及可能的应变效应。以下是计算InGaN量子阱带隙的基本步骤:
1. 合金带隙计算(使用带隙弯曲模型)
首先,需要计算InGaN合金的带隙,可以使用以下公式:
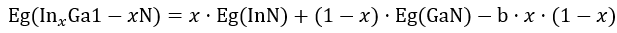
其中:
· 𝐸𝑔(In𝑥Ga1−𝑥N) 是InGaN合金的带隙能量。
· 𝐸𝑔(InN) 是InN的带隙能量,大约是0.7 eV。
· 𝐸𝑔(GaN) 是GaN的带隙能量,大约是3.4 eV。
· 𝑥 是In在InGaN合金中的摩尔分数。
· 𝑏 是弯曲参数,描述了带隙偏离InN和GaN带隙线性插值的程度;对于InGaN,𝑏 通常在1.4到2.9 eV之间。
2.量子限域效应
对于量子阱结构,带隙会因为量子限域效应而改变。量子阱的有效带隙可以通过以下公式计算:
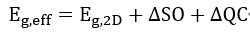
其中:
· 𝐸𝑔,2𝐷 是InGaN合金的二维带隙,使用带隙弯曲模型计算。
· Δ𝑆𝑂 是自旋轨道分裂能,对于GaN通常是0.34 eV,InN略小。
· Δ𝑄𝐶 是量子限域能,可以通过有效质量近似和量子阱宽度(L)计算:
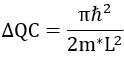
其中:
· ℏ 是约化普朗克常数(大约 6.582119569×10−16 eV·s)。𝑚∗是量子阱方向的有效质量,对于电子在GaN/InN中, ≈0.22𝑚0 ,对于重空穴, ≈0.5𝑚0 ,𝑚0是自由电子质量。𝐿 是量子阱的宽度。
3. 应变效应
InGaN量子阱中的应变会进一步影响带隙。应变可以通过以下公式考虑:
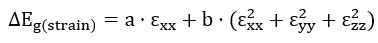
其中,𝜀𝑥𝑥,𝜀𝑦𝑦,𝜀𝑧𝑧 是应变张量的分量,𝑎a 和 𝑏b 是材料特定的应变系数。
计算步骤
1.确定InGaN合金中的铟含量(x)。
2.使用带隙弯曲模型计算二维带隙(𝐸𝑔,2𝐷)。
3.计算自旋轨道分裂能(Δ𝑆𝑂)。
4.使用有效质量近似和量子阱宽度计算量子限域能(Δ𝑄𝐶)。
5.如果存在应变,计算应变引起的带隙变化(Δ𝐸𝑔(strain))。
6.将所有这些值相加,得到量子阱的有效带隙(𝐸𝑔,𝑒𝑓𝑓 )。
需要注意的是,这是一个简化的模型,实际的带隙能量可能会受到应变、合金无序和其他因素的影响。对于非常薄的量子阱或特定器件应用,可能需要实验数据和更高级的模型来进行精确计算。