唐老师就是我梦中情师啊,遗憾的是课没完,但是给我打下了看起来很不错的基础。

安排
老师讲了许多课本上上面显而易见的东西是如何来的,这种通畅的感觉,比我吃了西梅还爽。

首先是罪重要的这个信号的对比
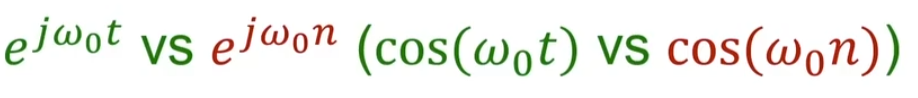
又从可视化的角度讨论COS
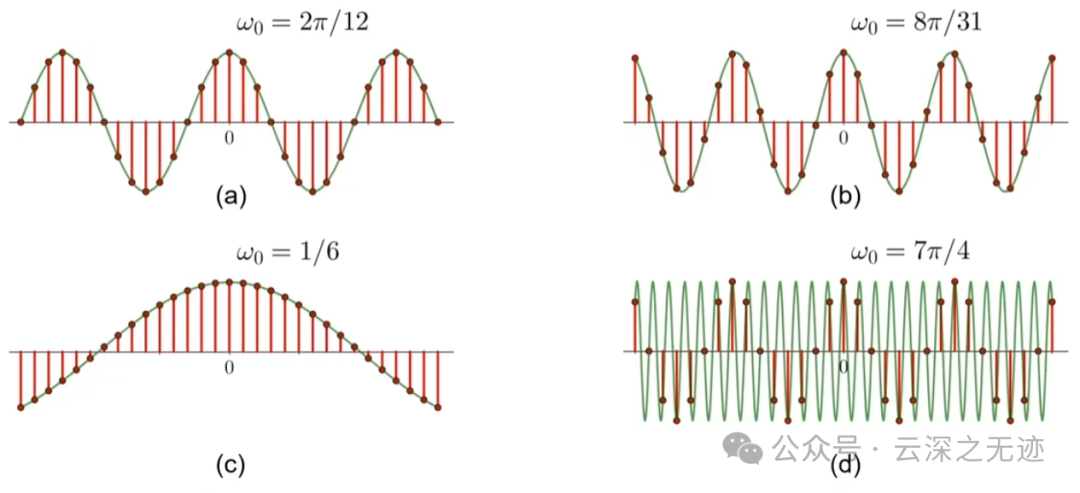
这个图说明了,离散的周期和l

在离散型中可以直接打开括号,明显公式成立的前提就是前一项为 1,也可以写成等式,经过观察 我怎么录音?2mπ其实是对应的整圈数

m圈,这个就更明显了

我们也可以写成常见的样子,一圈除以步距其实就是说明最低的圈数的倒数
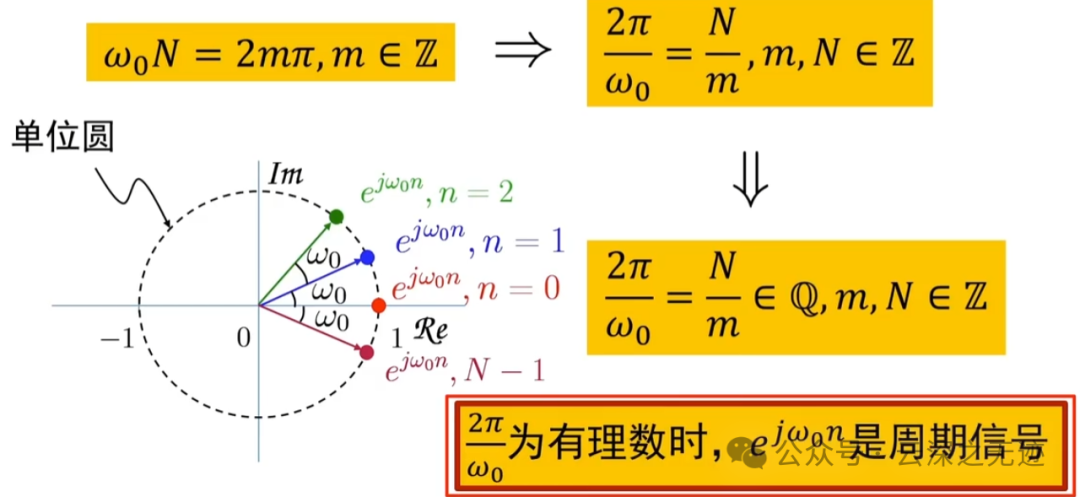
最后可以给出一个判别式,比值为有理数就 OK
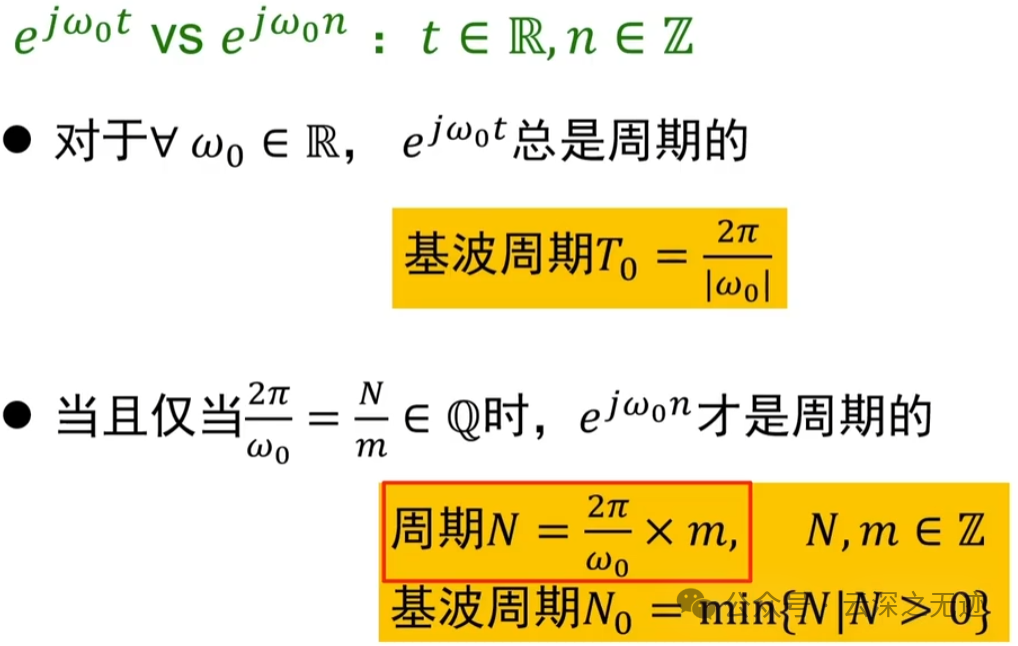
将公式变形,可以单独的把离散周期分离
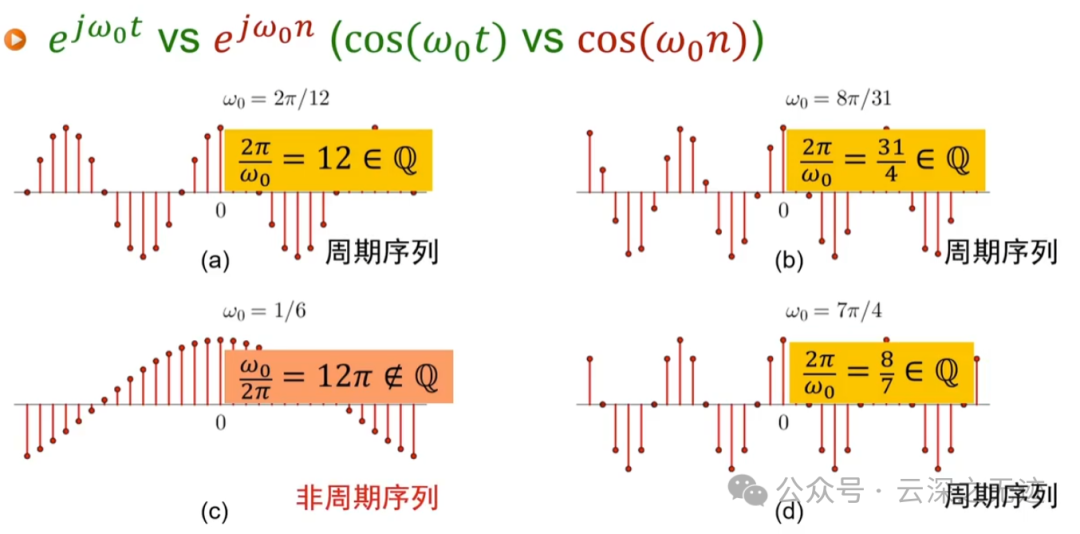
这个就是对上面判别式的一个例子

以上三个可以抽成一个公式
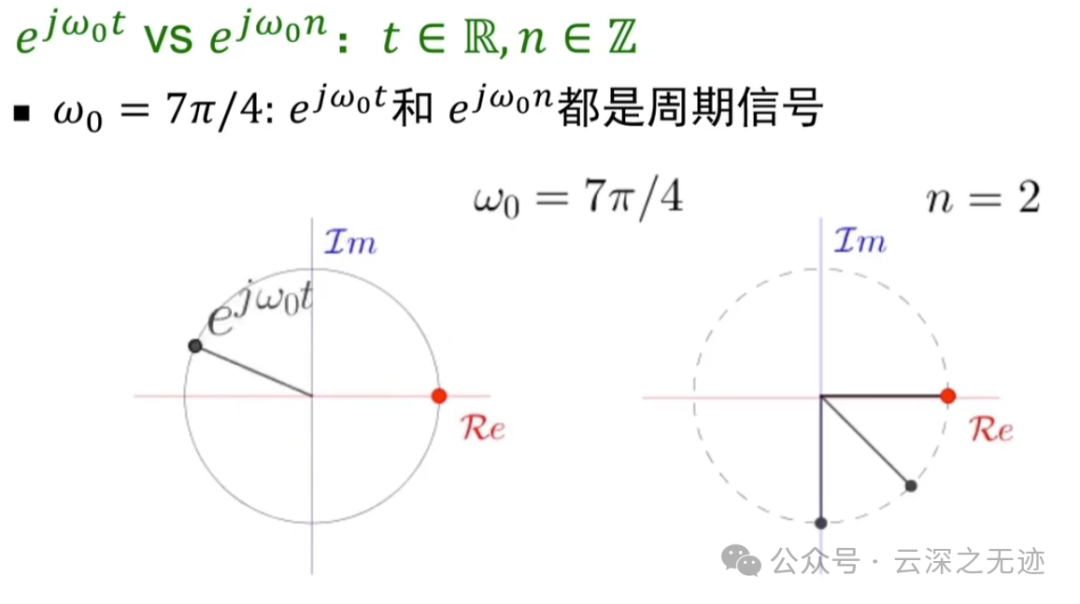
这里我们看这两个圈,第一个是t,连续的,看起来是逆时针,右边是顺时针转动。
那是不是就能说右面的角频率是:

?怎么解释
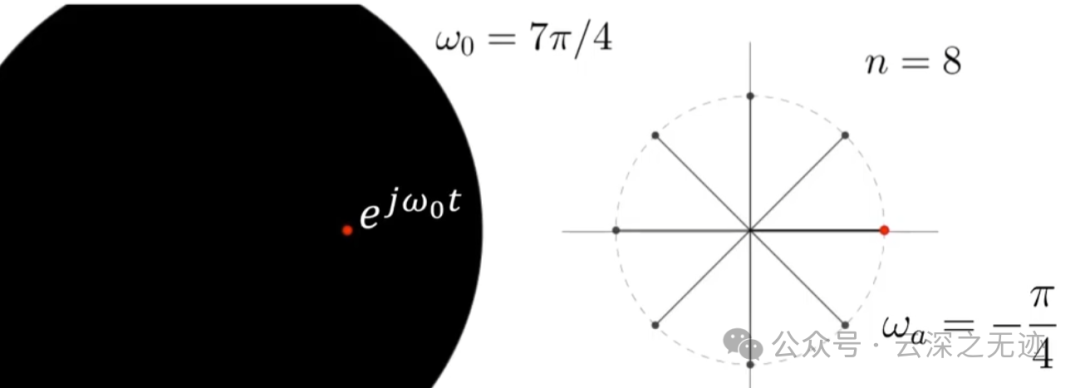
原因是我们不是所有时刻都可以看到这个信号
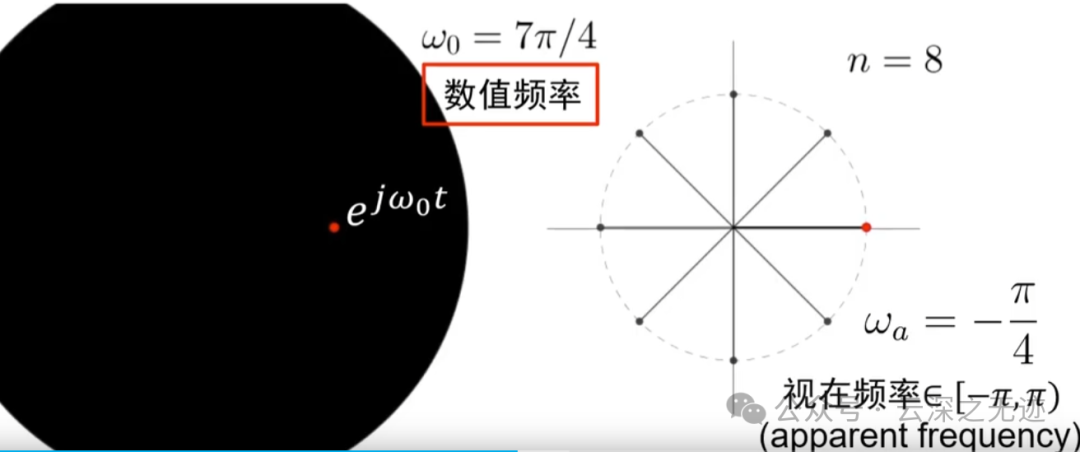
所以真正的旋转频率是数值频率,可以看到的是视在频率,就是可以看到的频率 
这个是想说明,我们对于一个离散型的取值,其实你无法准确地说明它到底是经过多少个周期后的数据,因为老是可以加几圈和现在的位置重合.
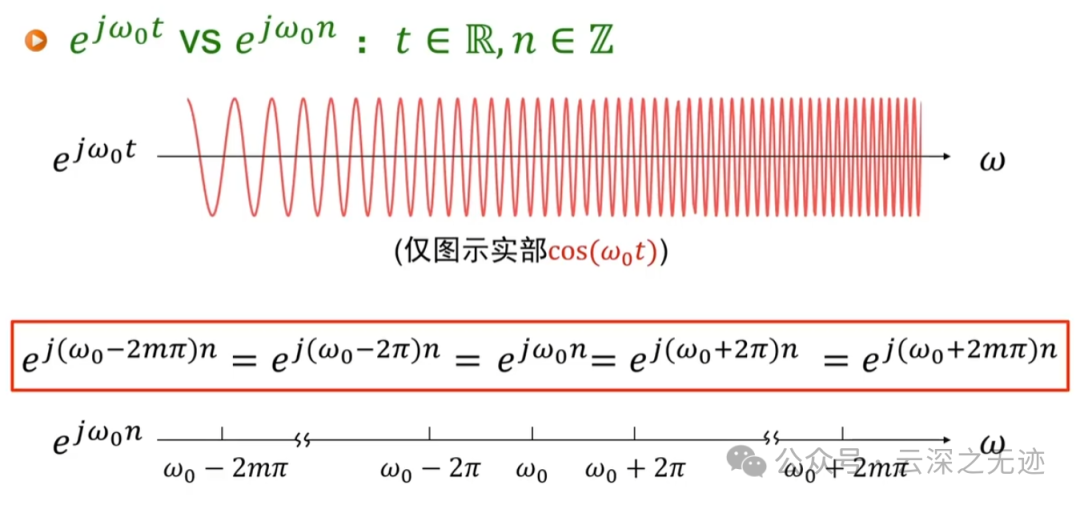
这个应该是对比,上面是指数信号的实部展开,下面就是是离散指数信号的展开,可以看到零零碎碎的取了几个点.,自变量都是角频率
没啥说的
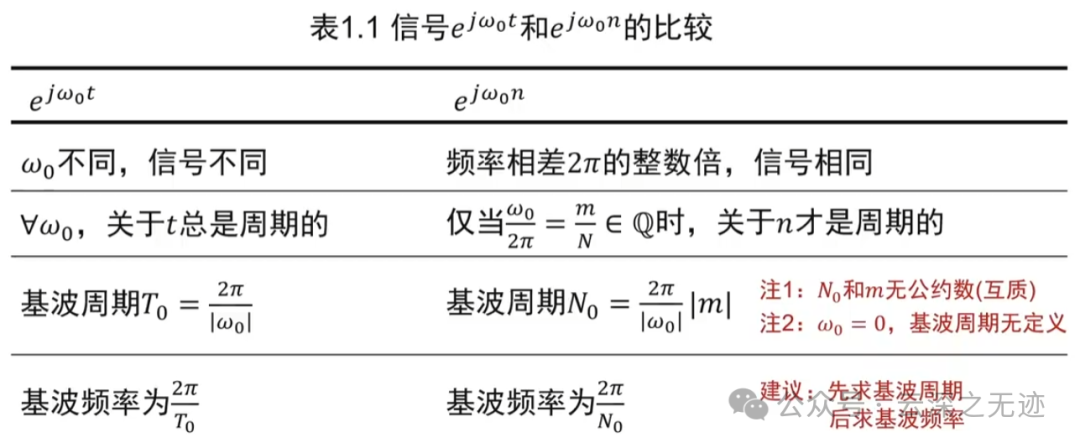
因为角频率不一样,当然,这个时序函数不一样,离散的话是有个 2π周期,剩下的显而易见.

内容属于二次加工,唐老师喂我,我喂大家
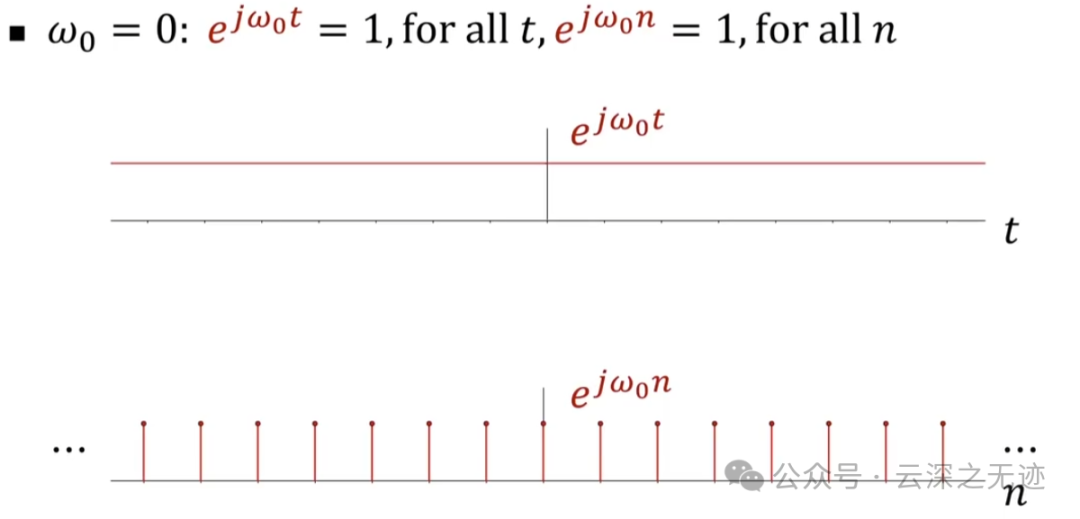
两个函数做对比

为什么复指数重要?因为微分不变性提供了一些有益的启发

老师推荐了这个书

随便说的数学建模

数值方法里面主要是差分方程


看看热闹

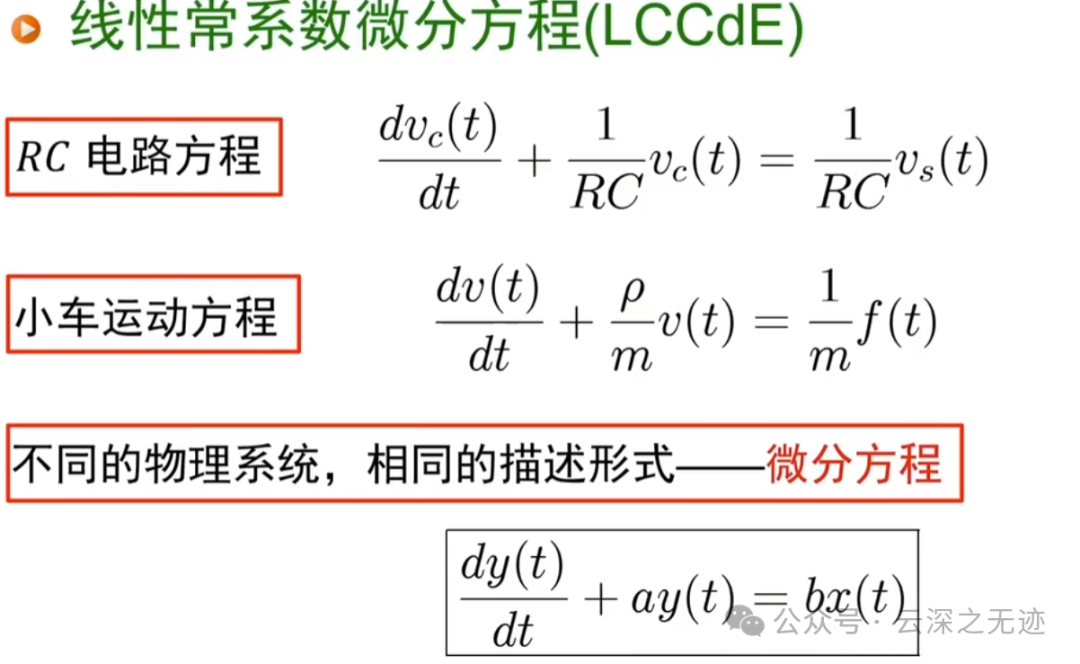
这个是小汽车的运动微分方程
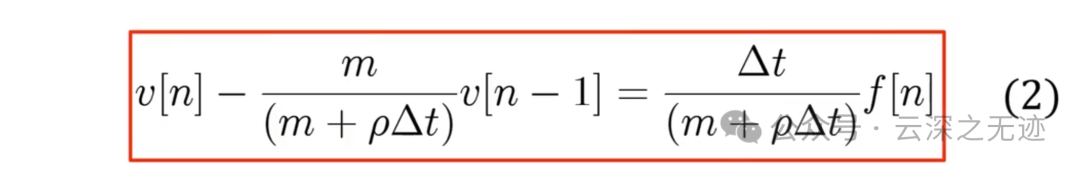
写成差分方程就是这样

这个离散的指数信号为什么是这样,这里给出一种解释
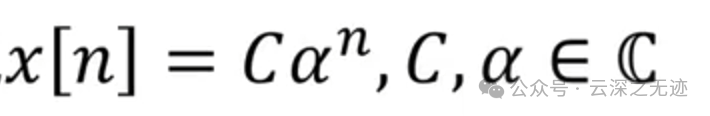
原则是让问题变简单
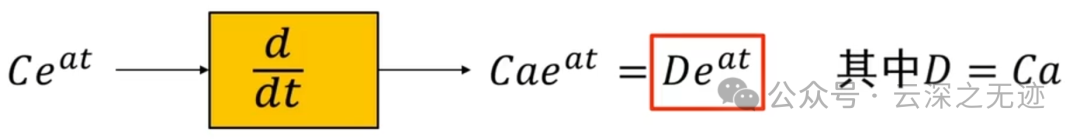
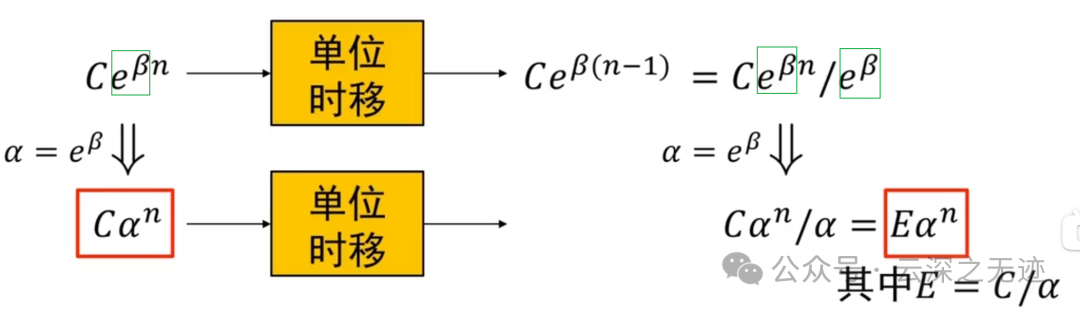
牛逼,就是说令了一个每次都出现的结构,做到了形式上面的统一
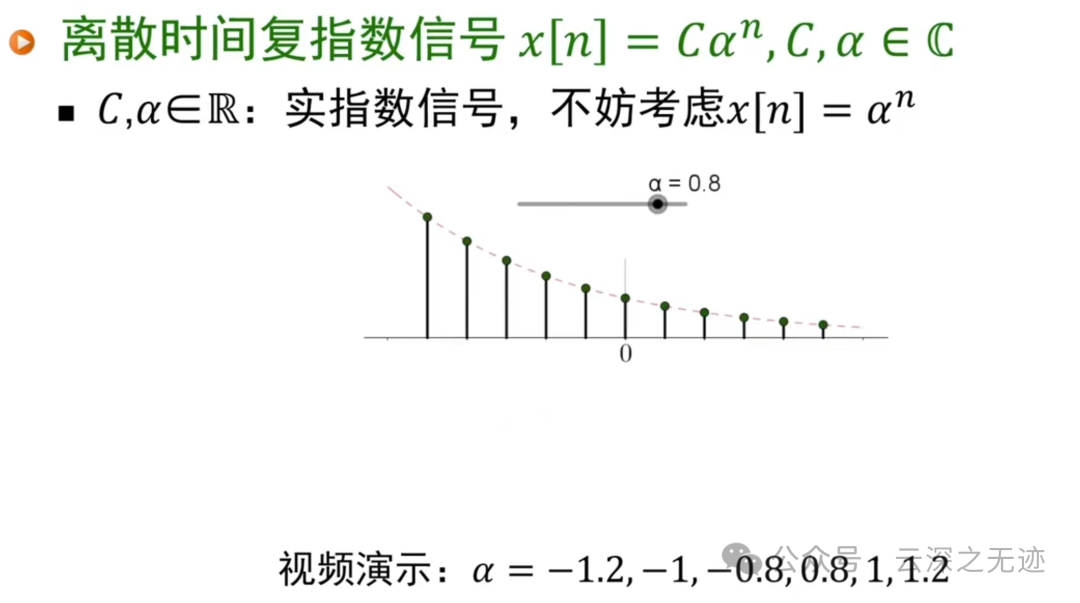
c 为 1
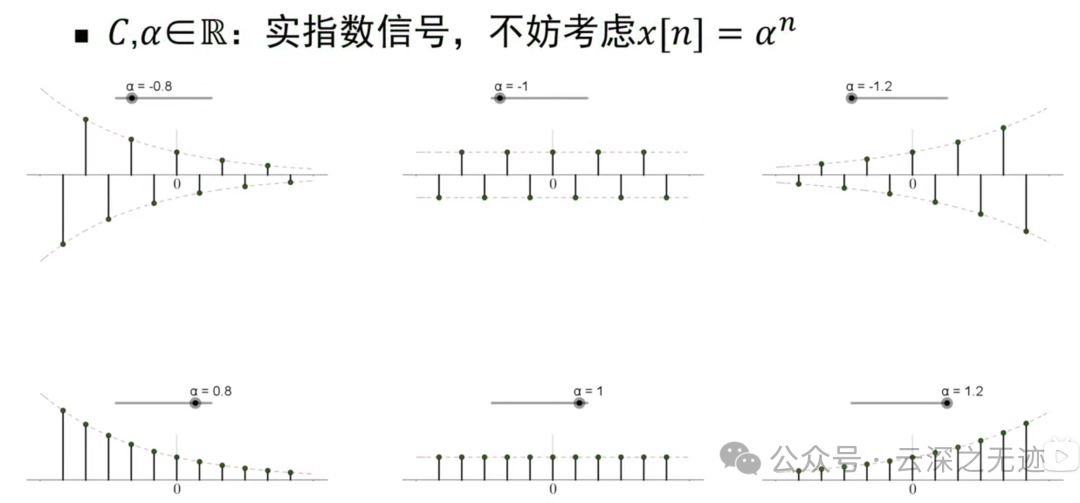

不同取值
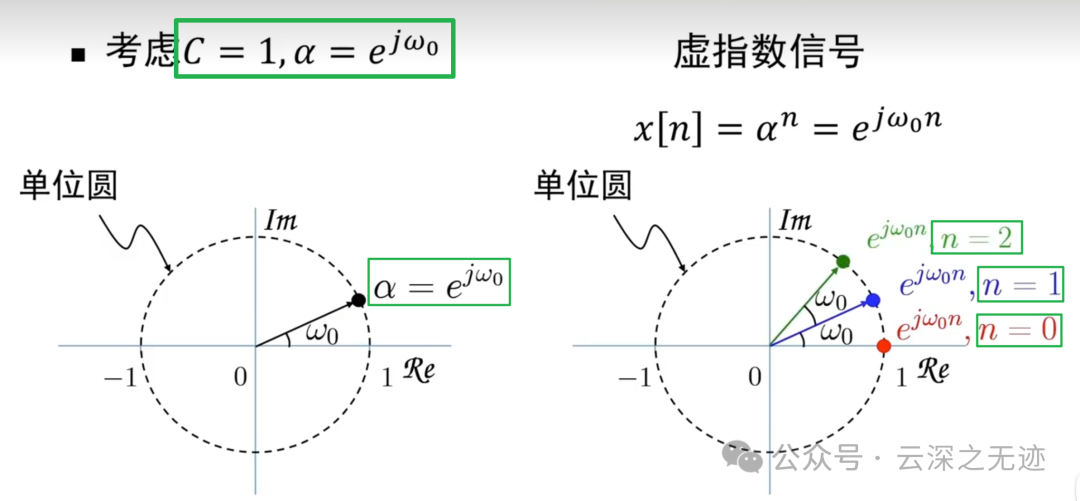
α取了 e 的 jΩ0 这个,c 还是 1
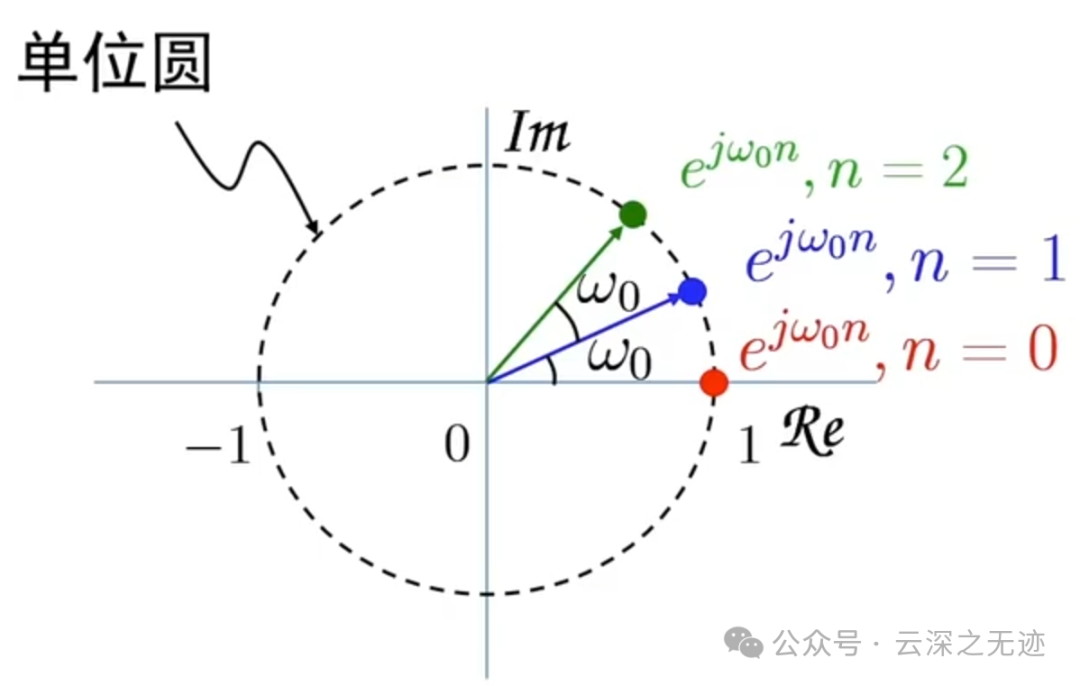
角速度的感觉
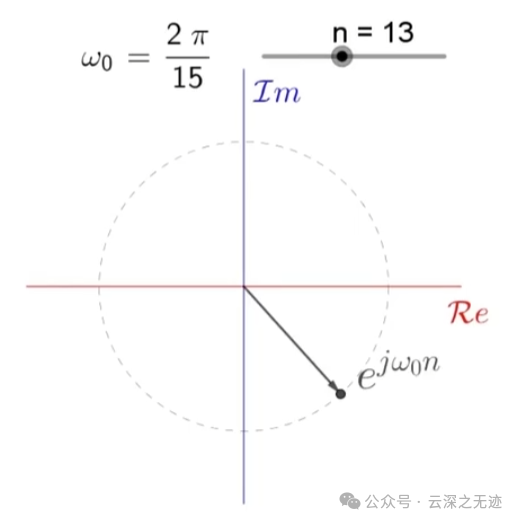
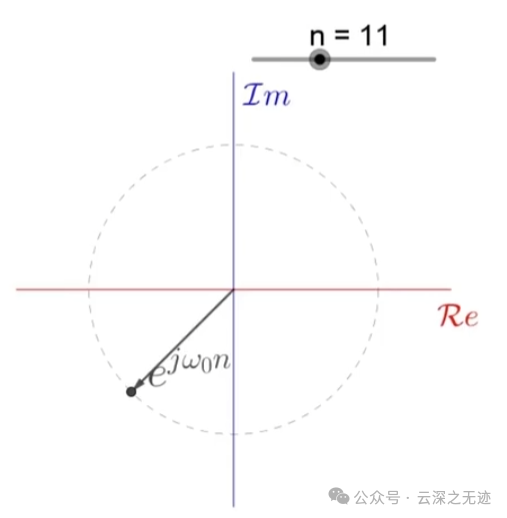
8
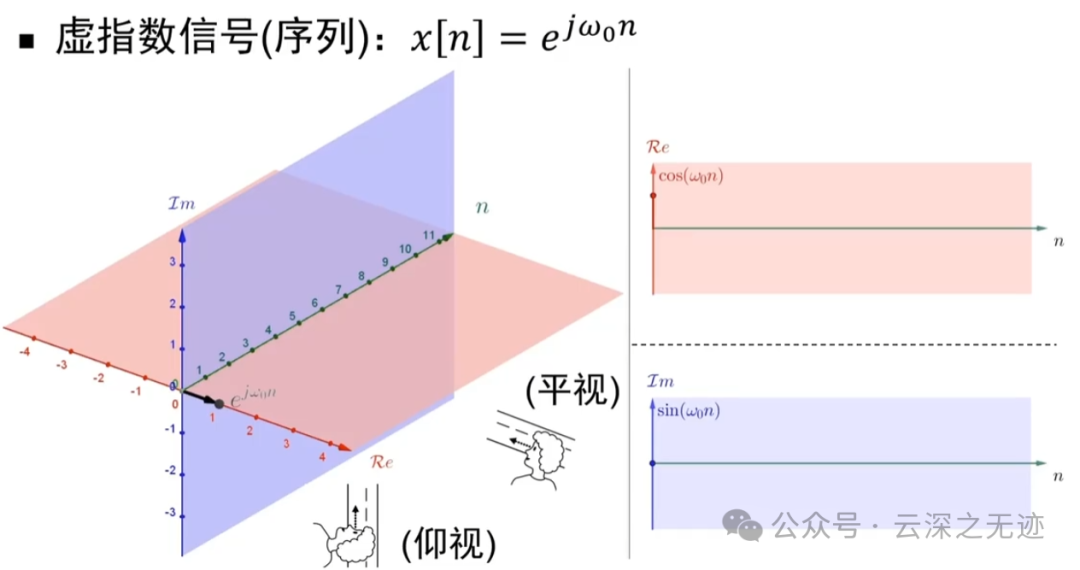
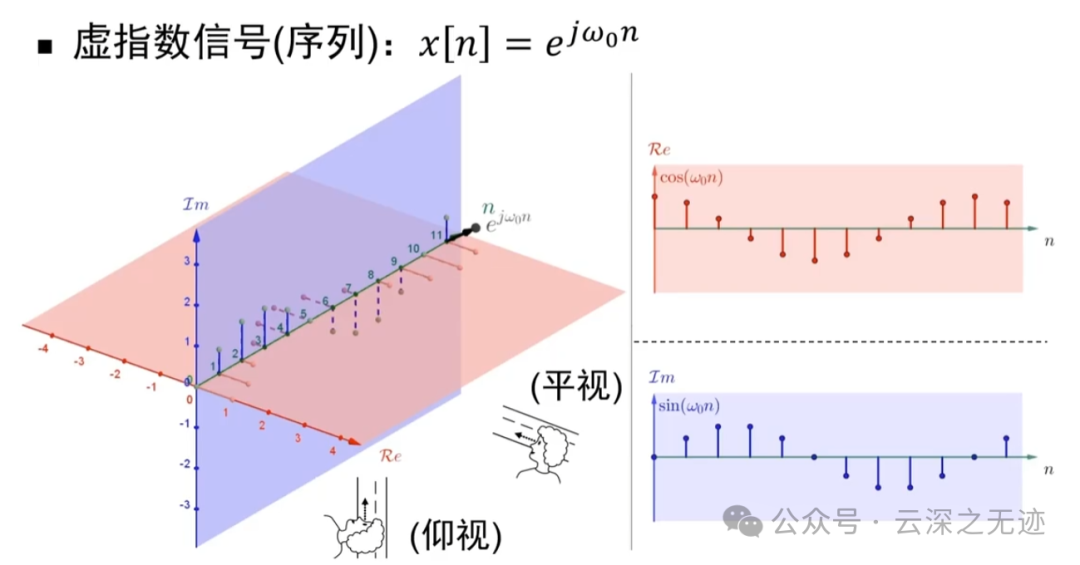
离散形式展开在两个平面上

离散也可以欧拉
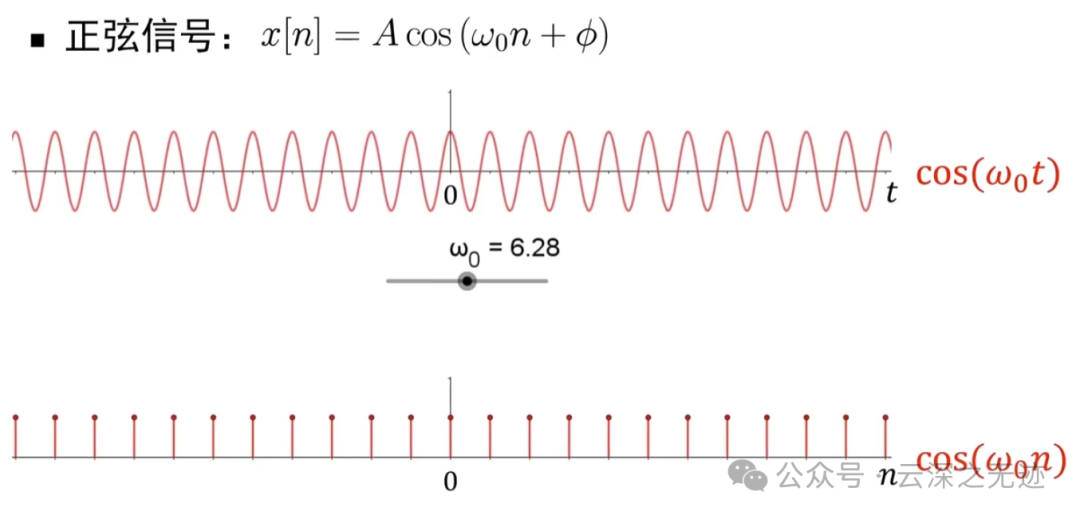
0 时刻,平平淡淡
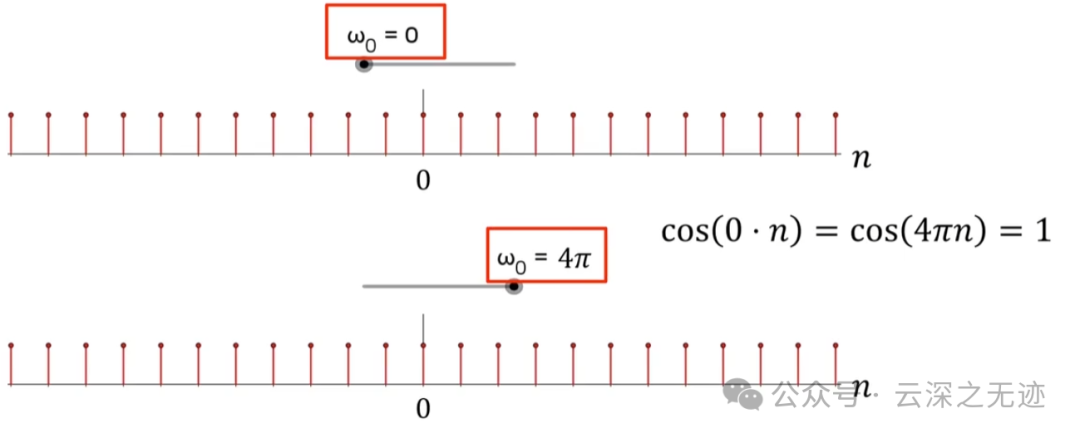
4π也是
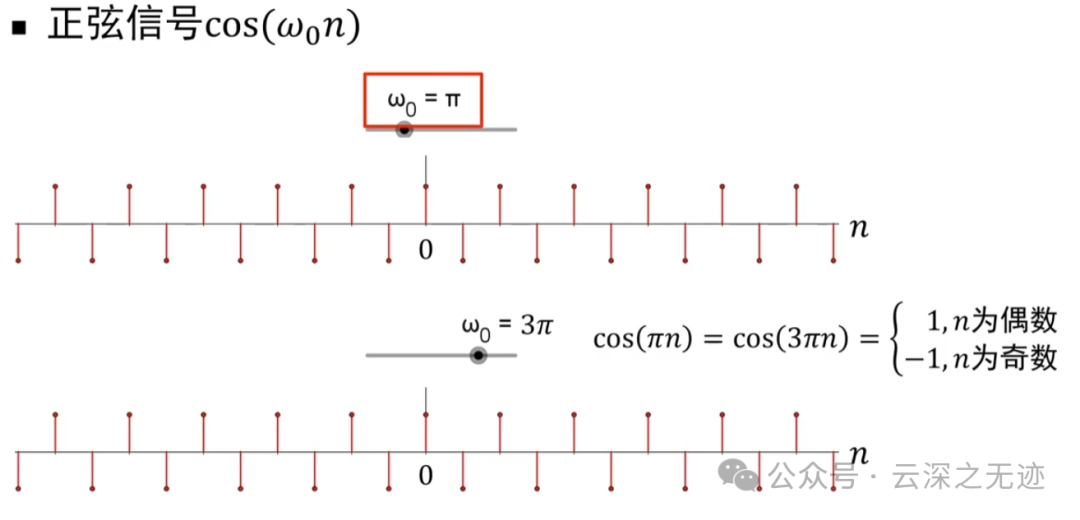
但是奇偶就不一样了
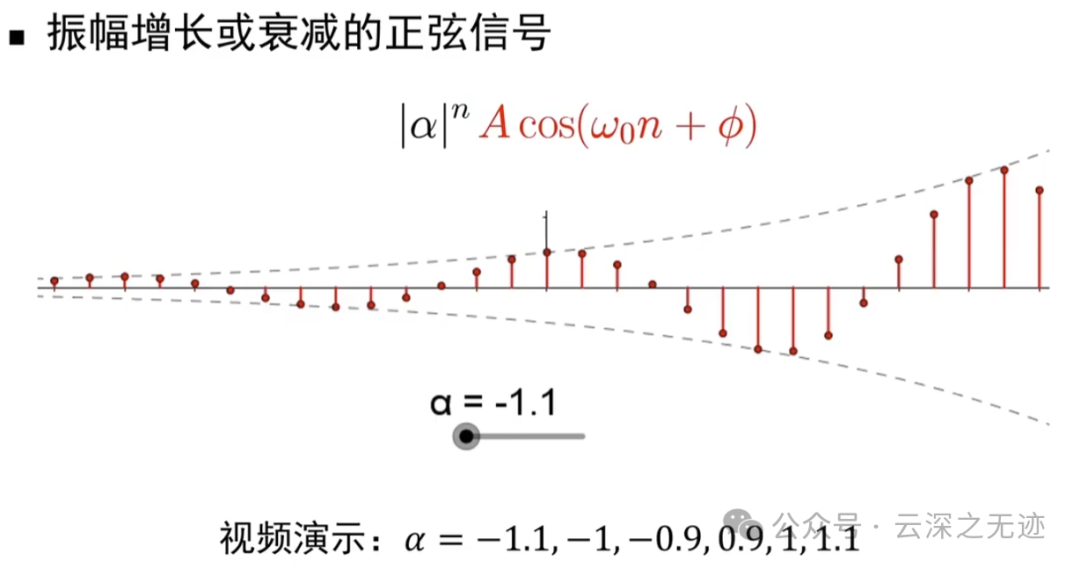
可以乘东西,相当于有个包络

这个地方注意,是调整了顺序,然后出现了模长和角度

把上面的引在下面可以展开,同样有两个图
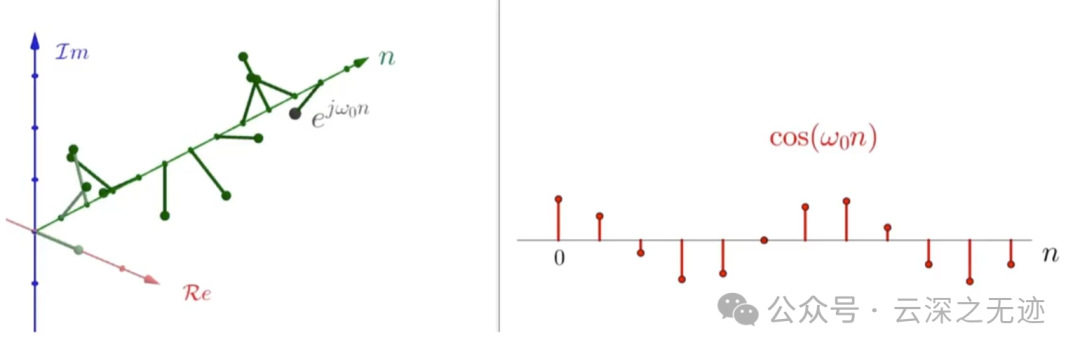
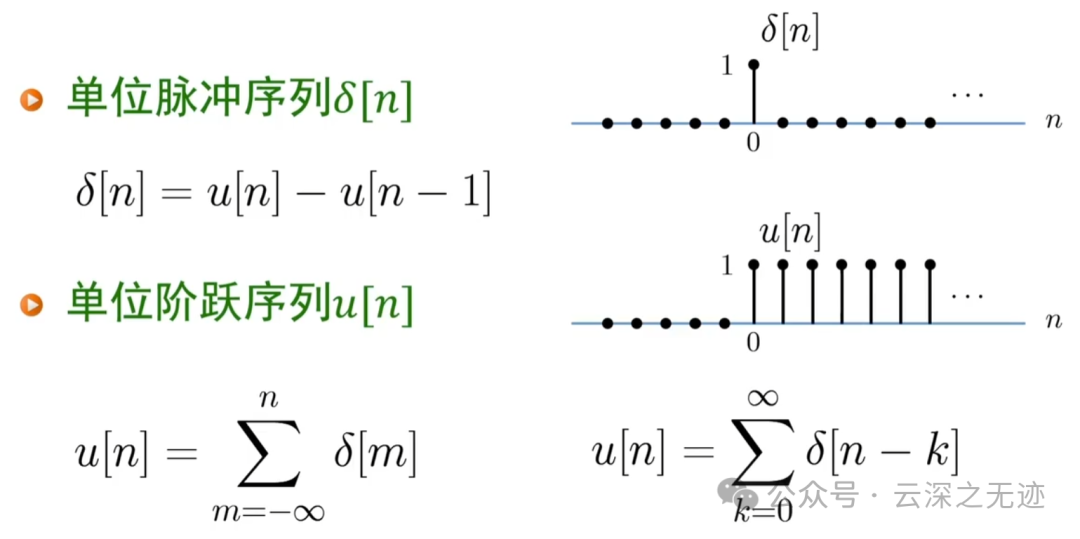
单位脉冲序列,单位冲击序列
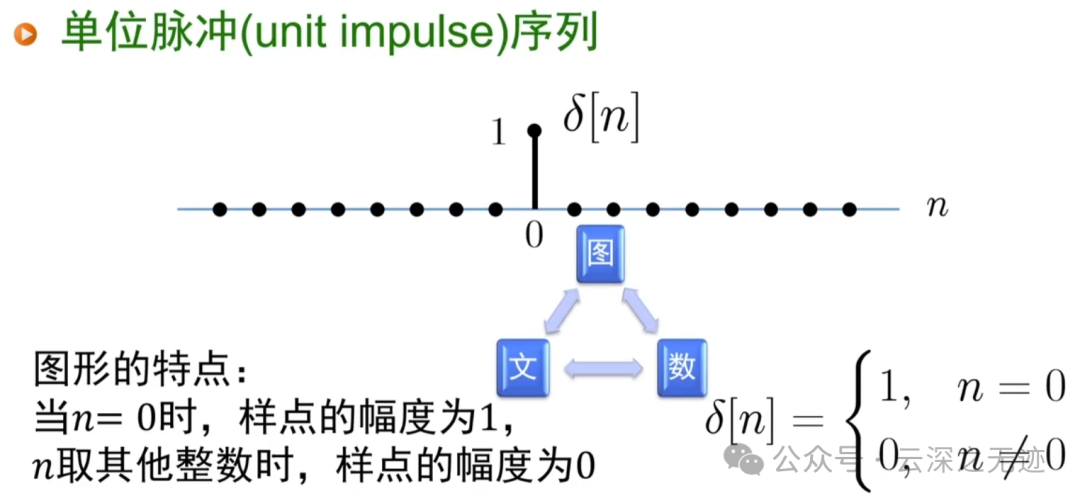
说话屌屌的,喜欢
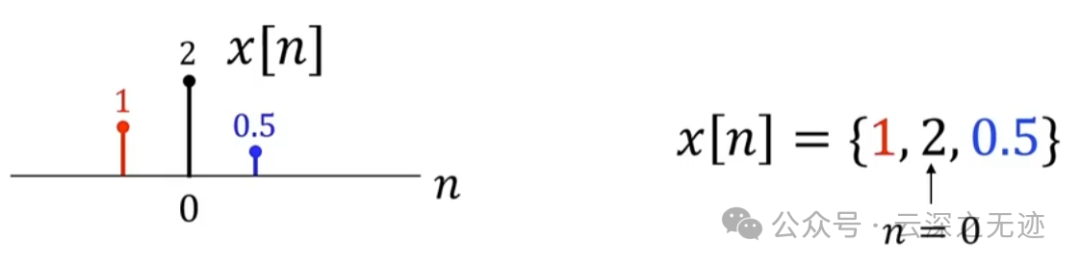
这个一种描述方式,一个数组

使用位移的形式
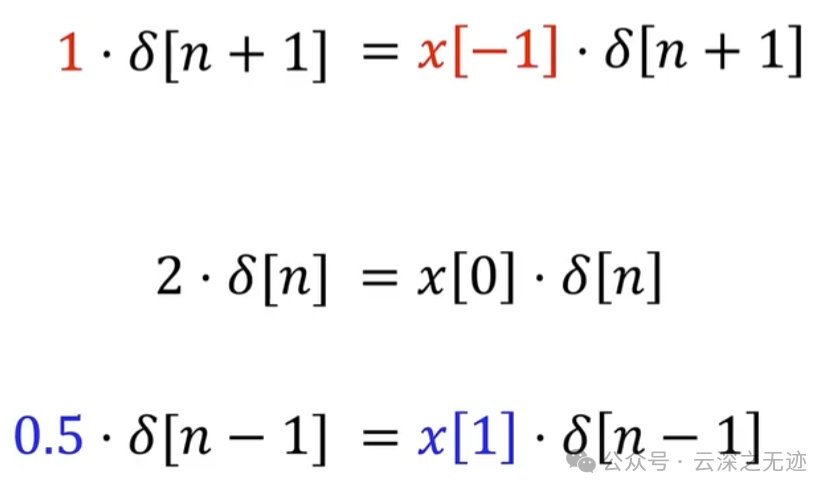
我们打开以后和上面一样,值+时移
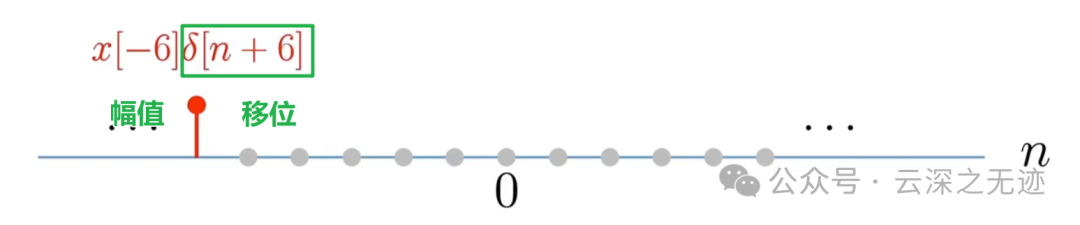
这个应该也是说了同样的事情

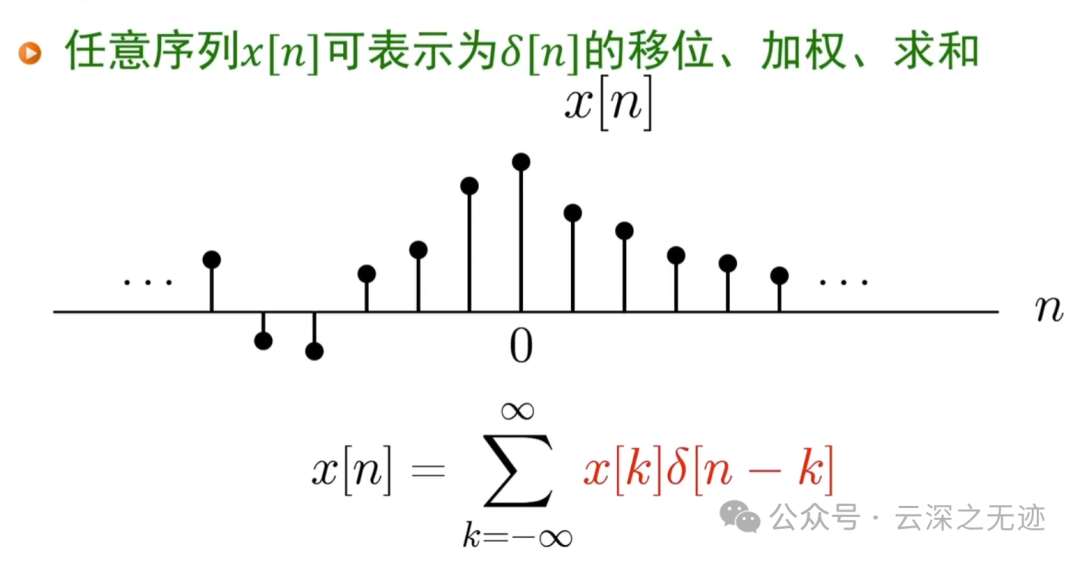
上面信号的结构,也可以看作是线性代数无穷维空间里面的每个基乘以对应的系数的形式

有感觉了没有

这里也是
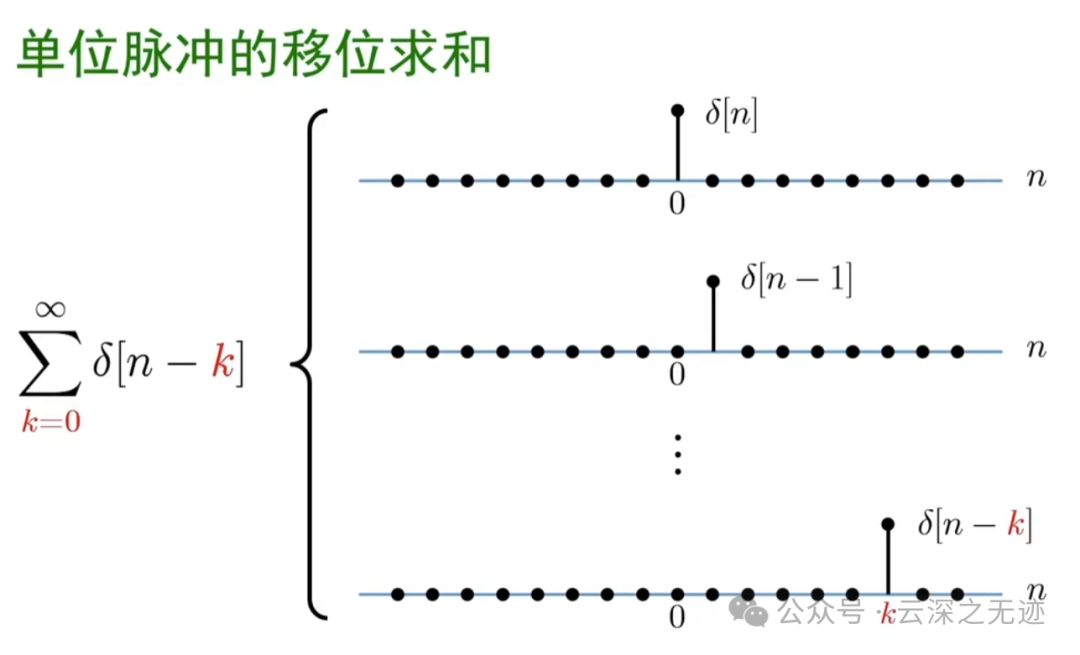
这叫位移求和
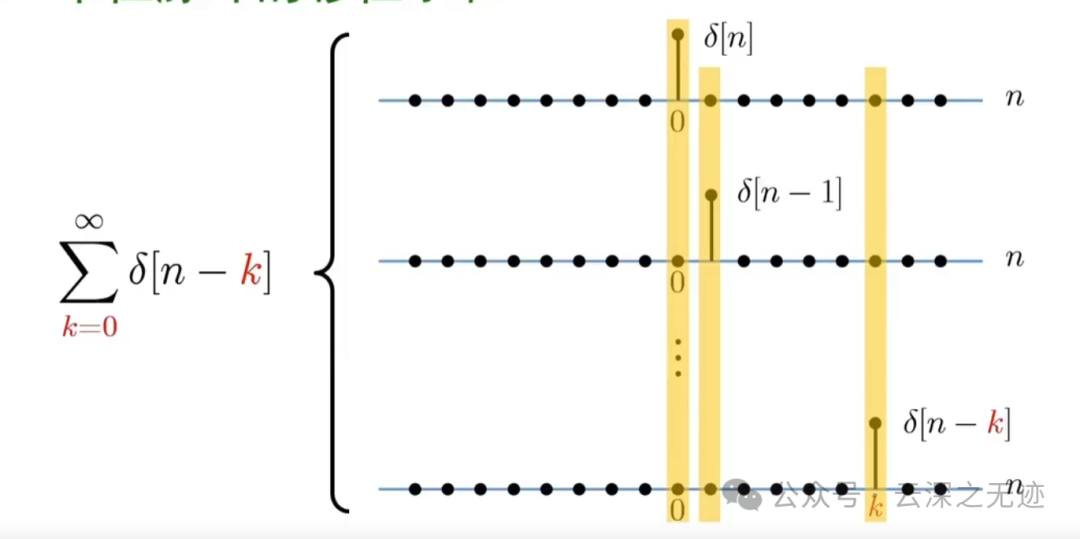
加的时候是每一个对应的位置,隐隐约约其实有点卷积的感觉了

变量替换,然后纯数学推导
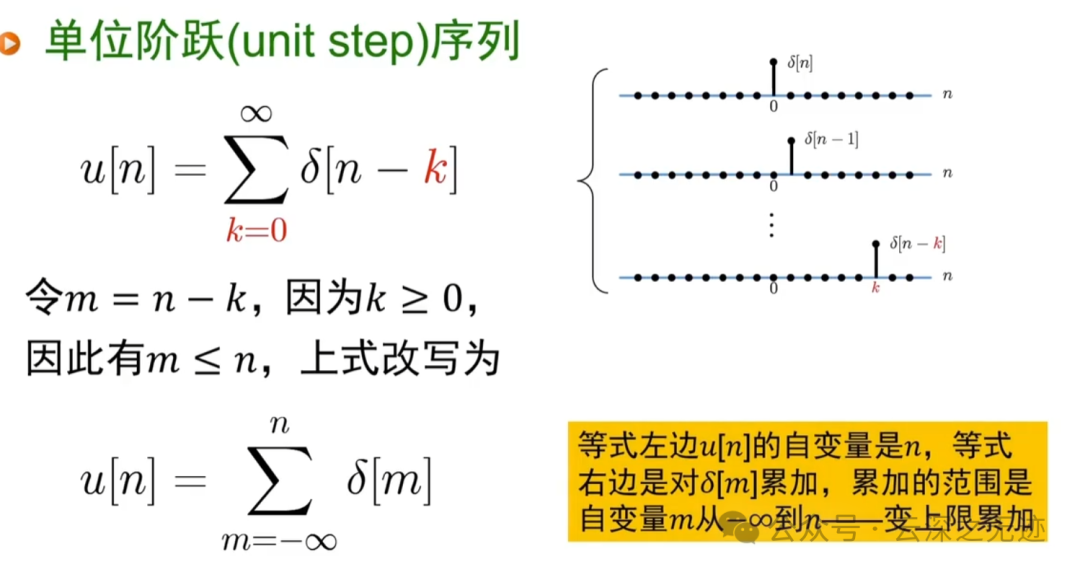
上面等式描述多个序列求和,多个序列相同时刻的幅度相加,下面描述序列的累加,所有样点的幅度相加
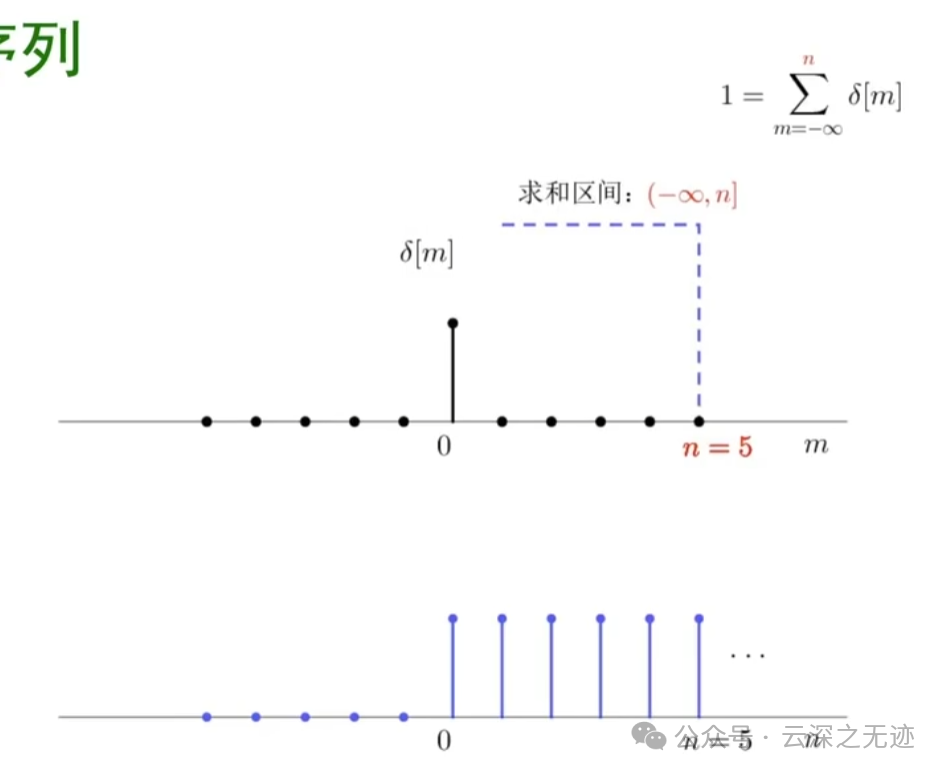
注意看上面的变量是m,下面是累加结构
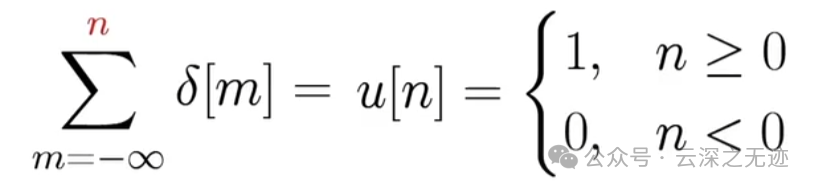
符合这个公式

这个样子的东西描述了累加器


x

下个视频要回答的问题

对应教材1.4
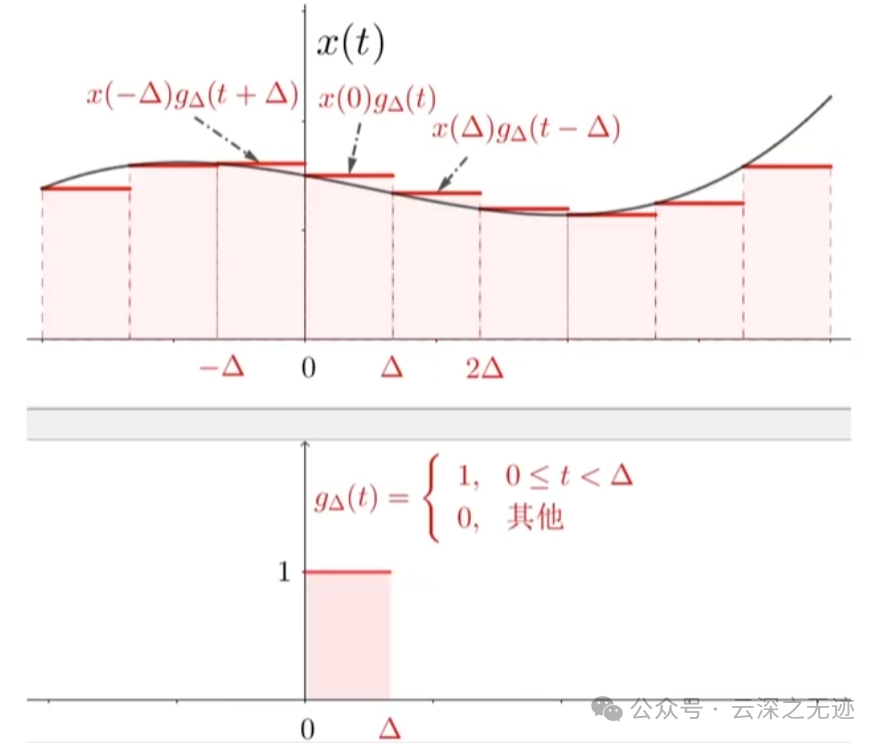
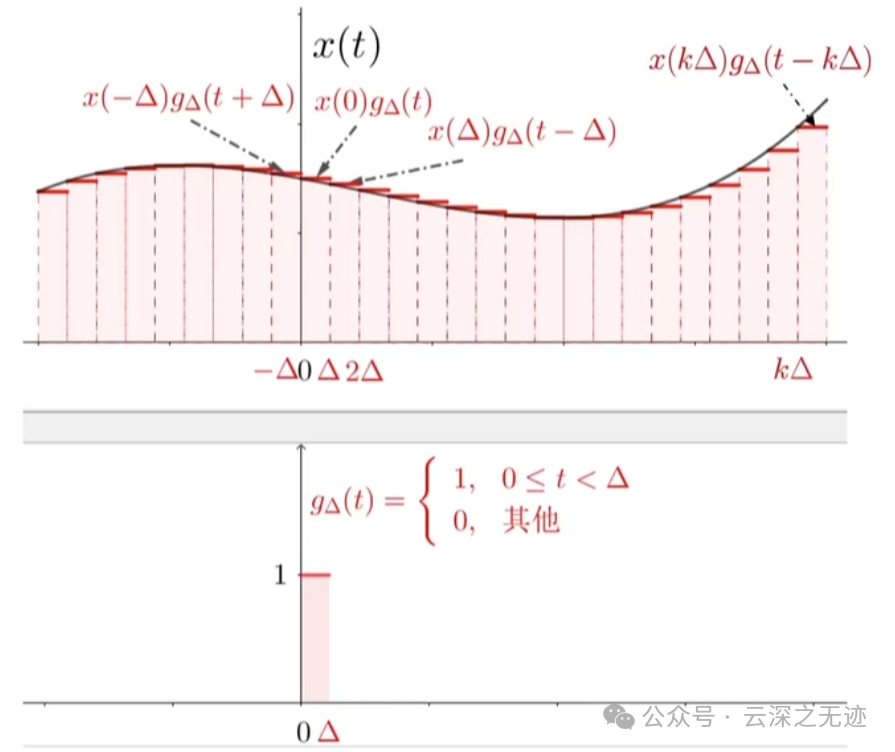
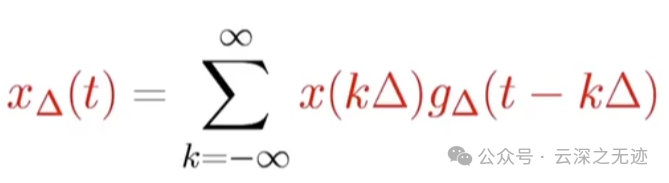
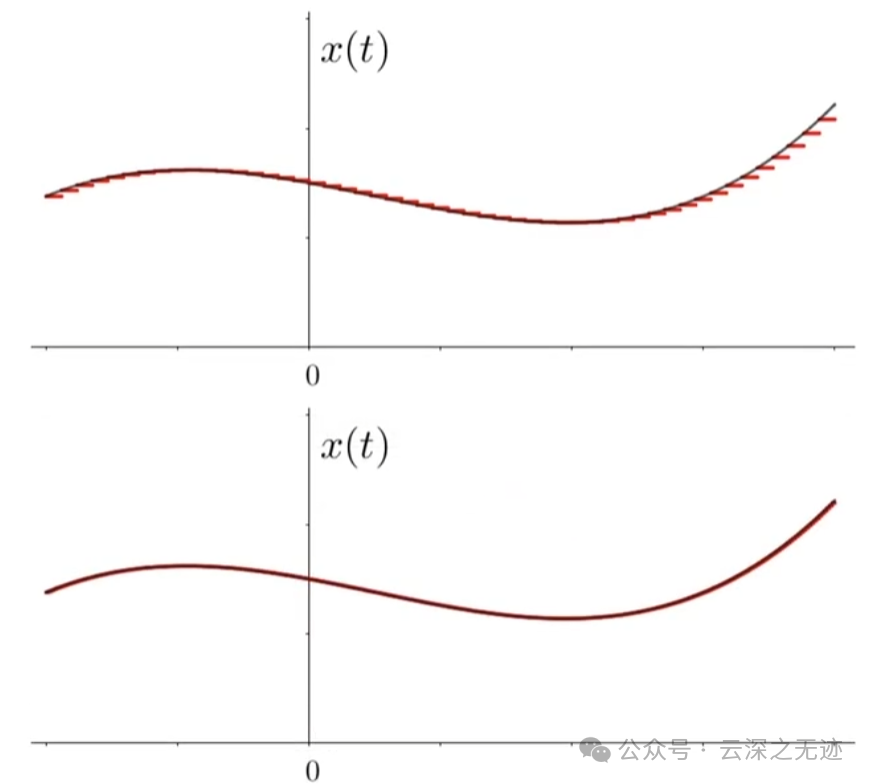
直到很细的时候
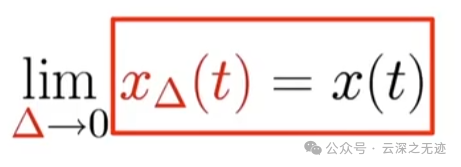
红黑相等

对比看,离散求和变成了积分,kδ也变成了连续变量μ,就缺一个微元变量了
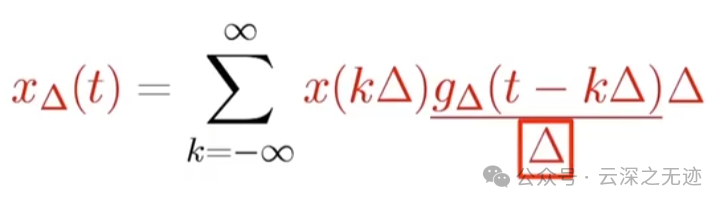
这个操作是直接乘一个微元,但是又多一个除一下,前面是时序函数肯定动不了,所以就放到后面的函数
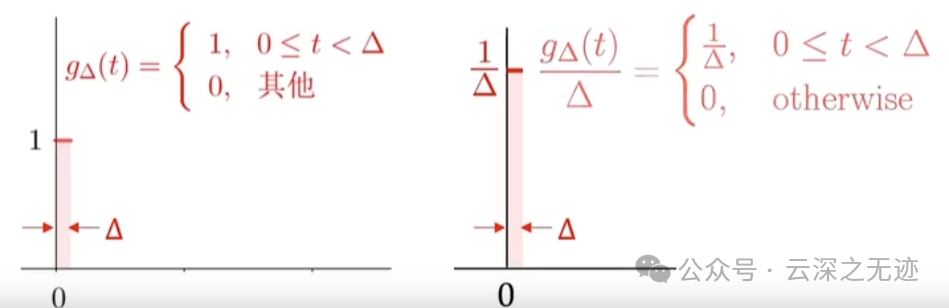
我们把右上面的函数计为

这个样子了
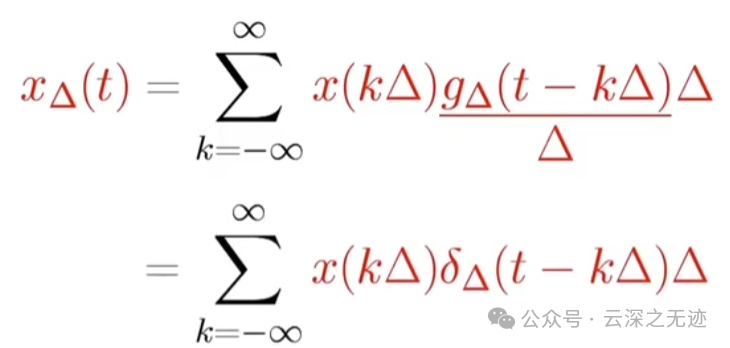
然后把里面的变量重写
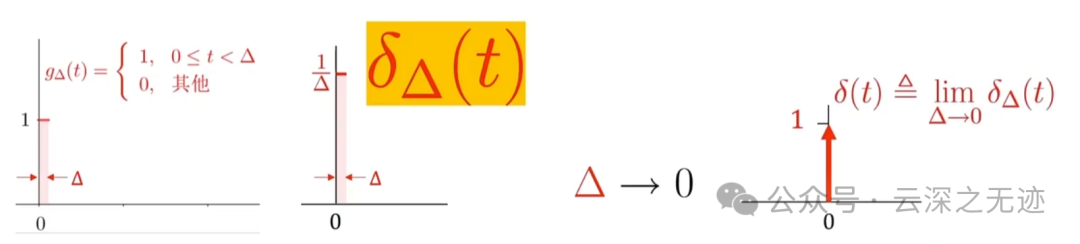
考虑当δ趋于0的时候,就是时间无限小,那这个强度或者是幅度就是无限大,后面面积还是1
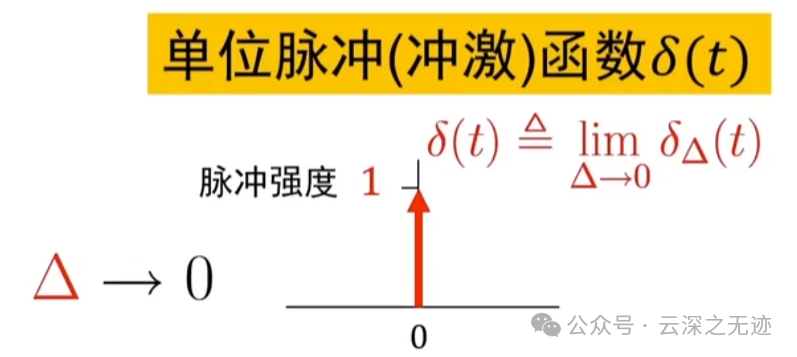
也就是说,我们其实是从离散的世界来的,先拿门函数,就是阶梯的信号模拟时序函数,但是太宽了,就让门函数关门,往小关。然后很密集的时候,进入了微积分的世界,在数学表示上面从求和变到了积分,通过对里面最小的门单位序列的研究,又抽象出一个单位冲激函数,至于为什么是单位1.
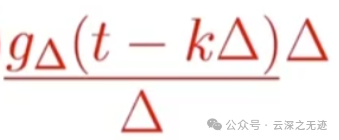
其实是公式的原因,第一次全部都连起来
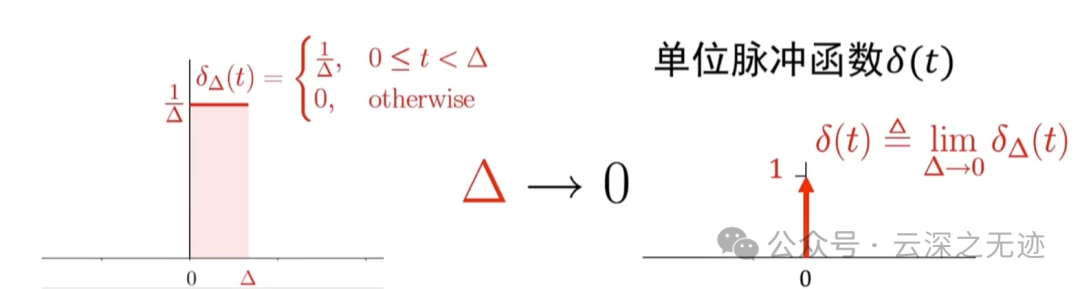
这个就是过程
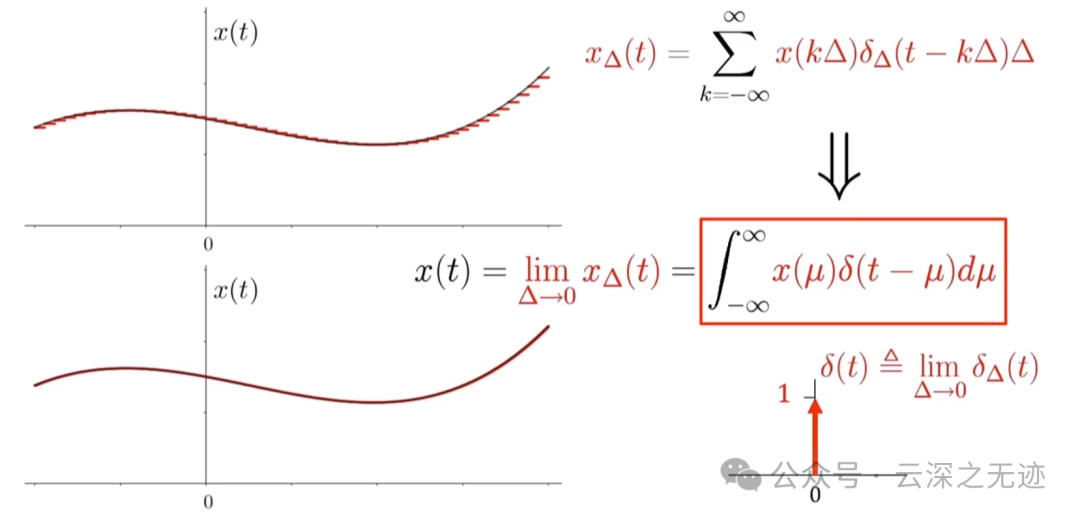
我们就完成了这样的转换
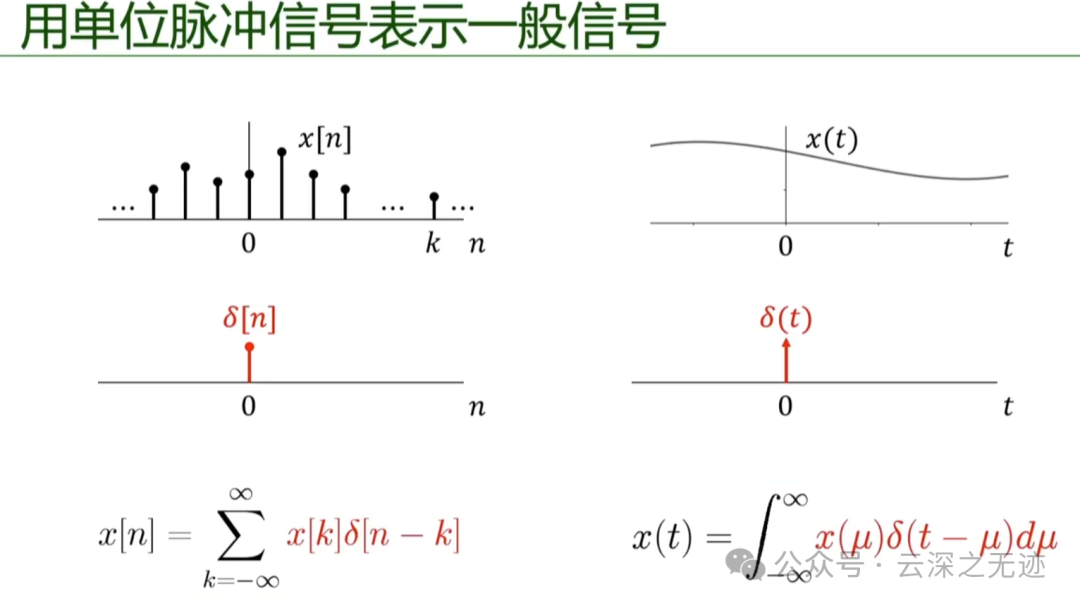
对比的看,时序上面还是不那么容易理解
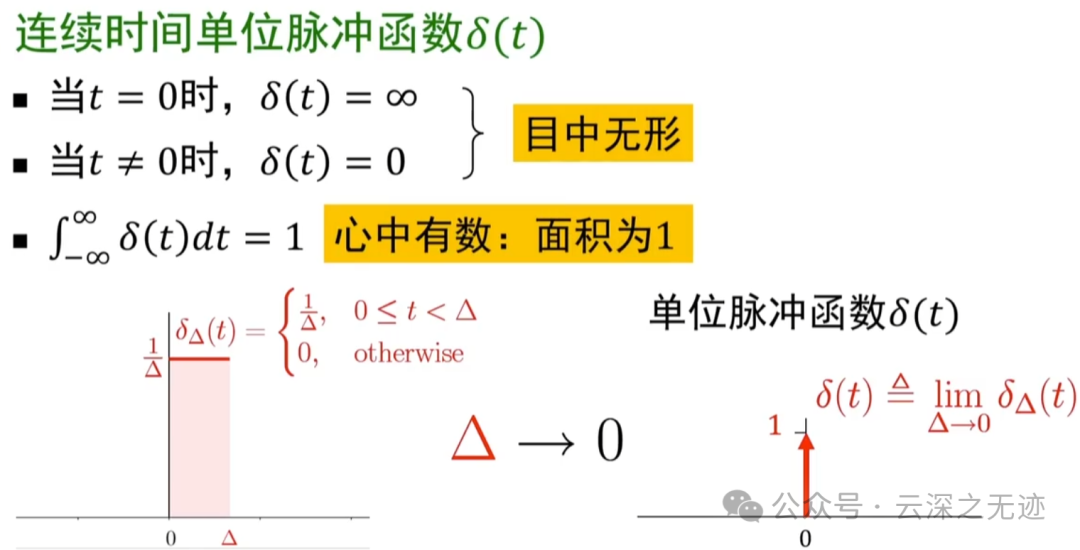
这个函数的性质,前两个是你看图像就可以得出的,但是最后这个是计算出来的。

看不见,看不见

如何表示一个连续时间的单位阶跃函数呢?
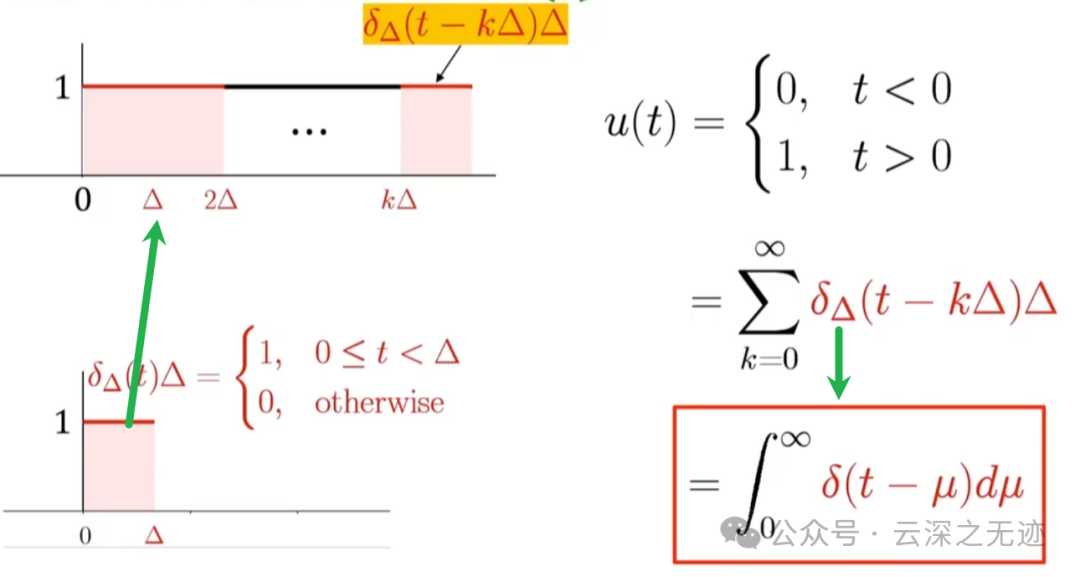
先把下面的门函数限制的一个单位为一的小格子,右面是公式上面的变化

公式在数学的角度做了变换,做了变量代换
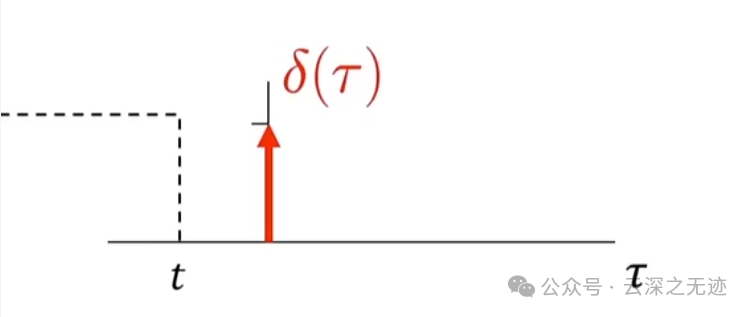
这个是t为负数的情况
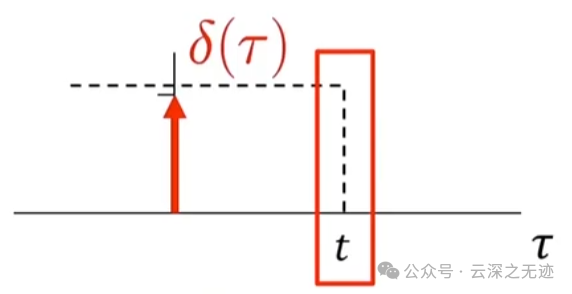
t大于0
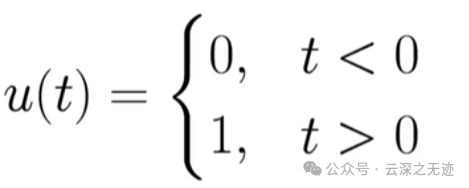
这玩意儿一摆,不就是原函数了

这张图里面信息太多了!我们说,左边的阶跃信号求导是不是右面呢?如果说是,那你就把数学书扔了,瞎几把学。求导的前提是连续,很明显,这个是我说的间断点,所以求不了到,至少是我们学的高等数学上面。所以就这样,又定义了一个单位斜变信号,是一个分段的函数,三段哦。我们对这个0~δ的区间求导就可以得到右面,然后这个导函数再趋于0就的得到了上面的冲激函数,反过来斜变信号和阶跃信号建立的联系,太通透了讲的。
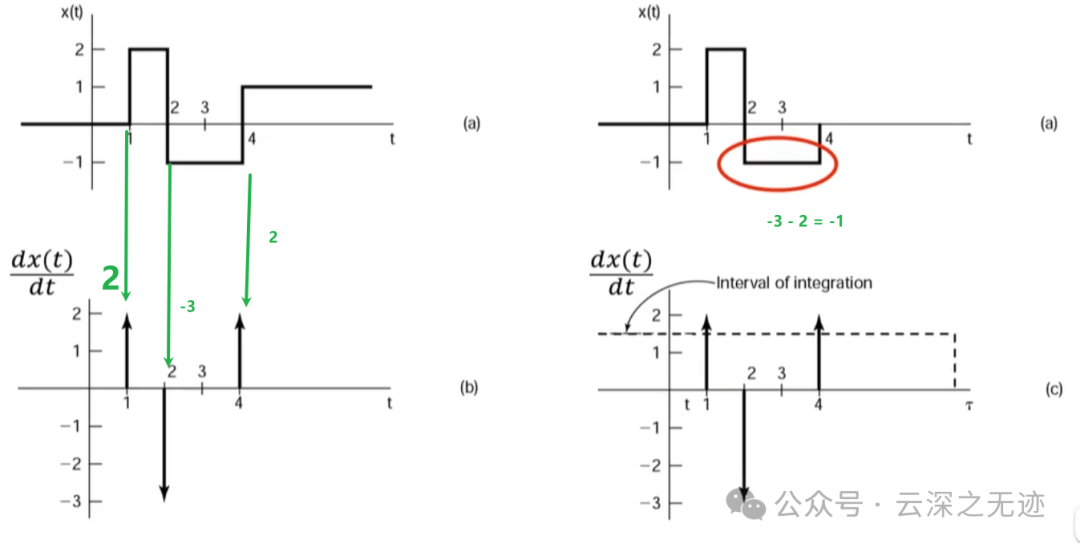
每次的积分结果其实都是时间点之后的求和

这样也可以理解,u前面的数字是幅度,符号是冲激的方向,括号里面是时间位移,

看不懂
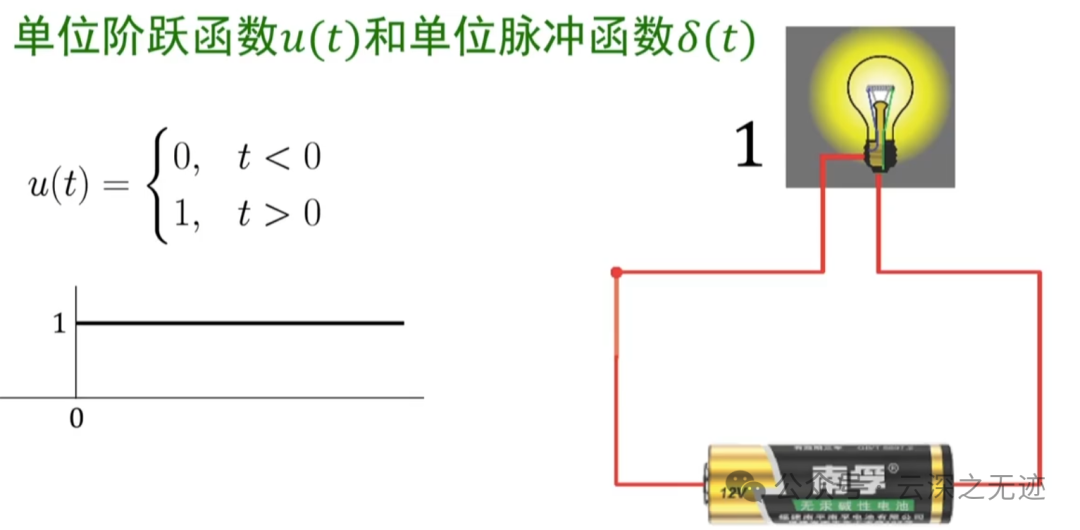
开关信号
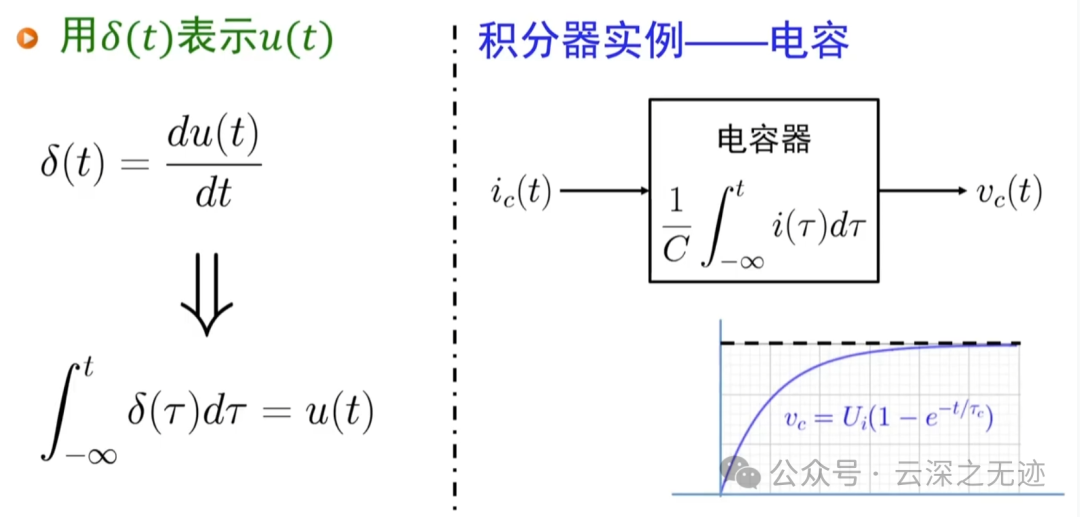
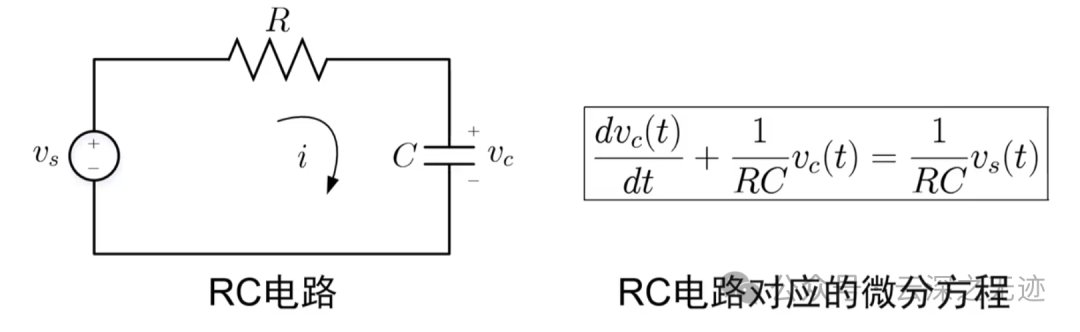
你看这个电容器是不是就模拟了阶跃信号
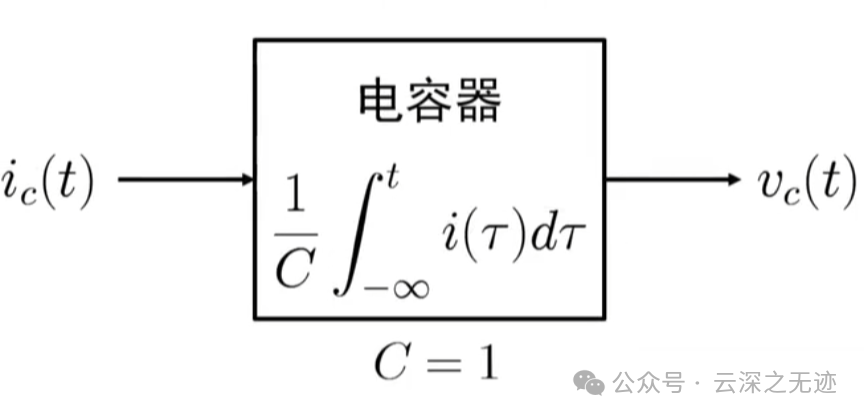
一个真实的物理模型
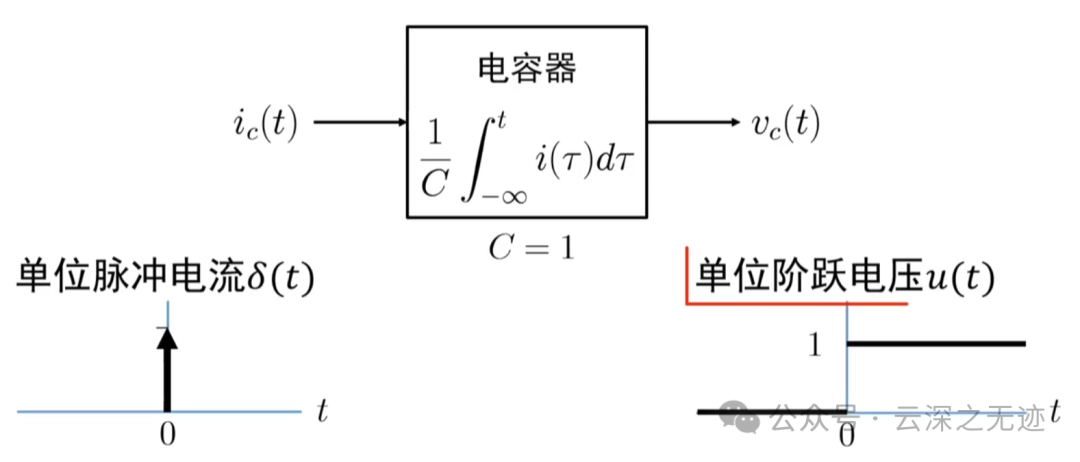
电流引起了电压的变化
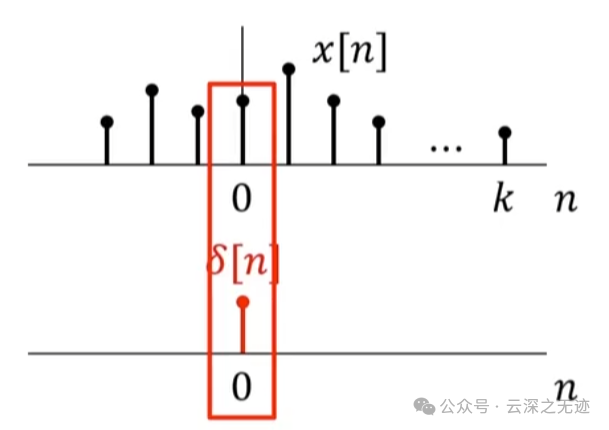
在离散里面,一个x[n]乘一个单位冲激
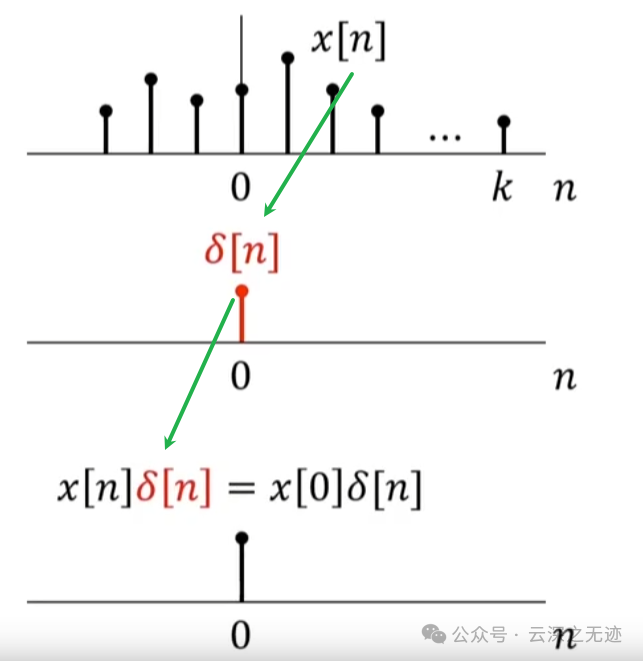
就是这样,等于x为0时刻的值
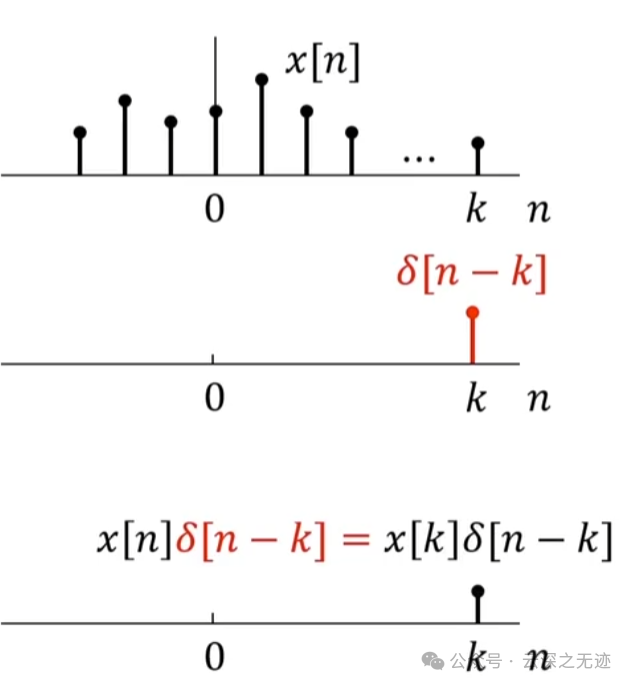
同理我们可以乘时移,一个序列乘一个时移的冲激=k时刻的函数值

我们要知道冲激函数移动只是因为它只是在0时刻为1,假如不移动的话,序列乘它还是为0。

真骚啊,比我都学的快,滚出去
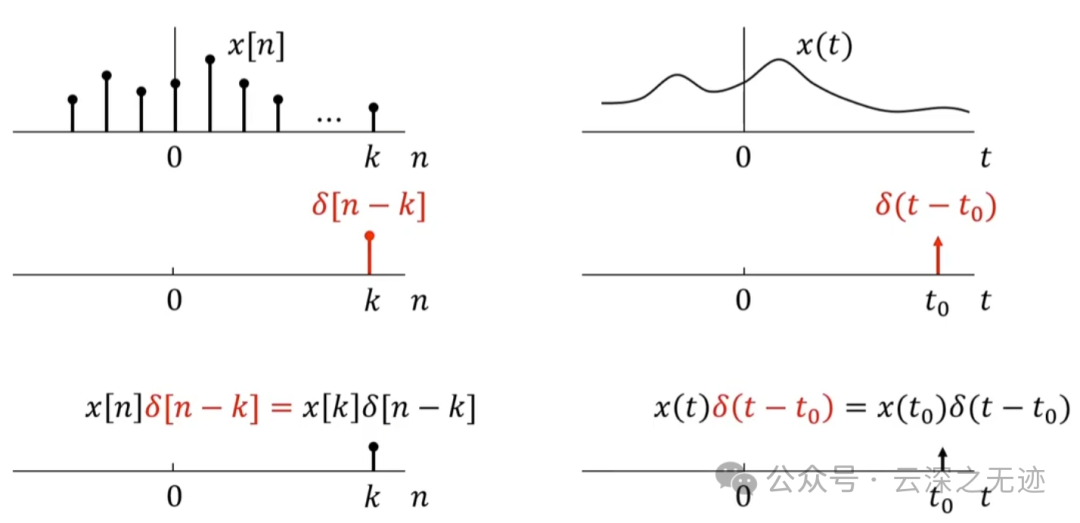
现在看就是离散和连续的,感觉都好理解
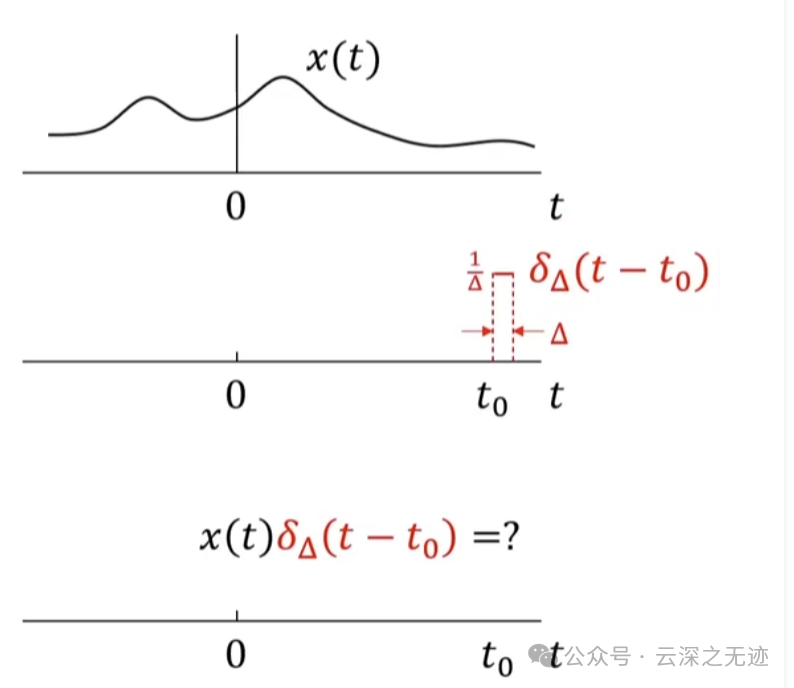
老师说推导性质怕看不懂,就可以使用这个东西同等的使用
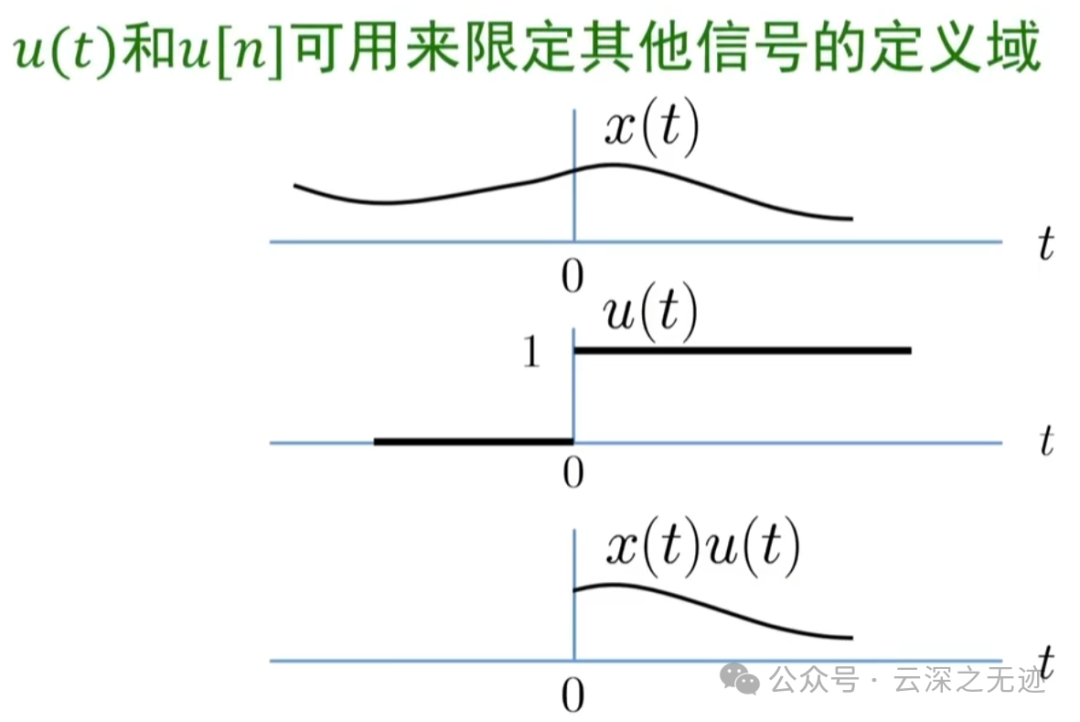
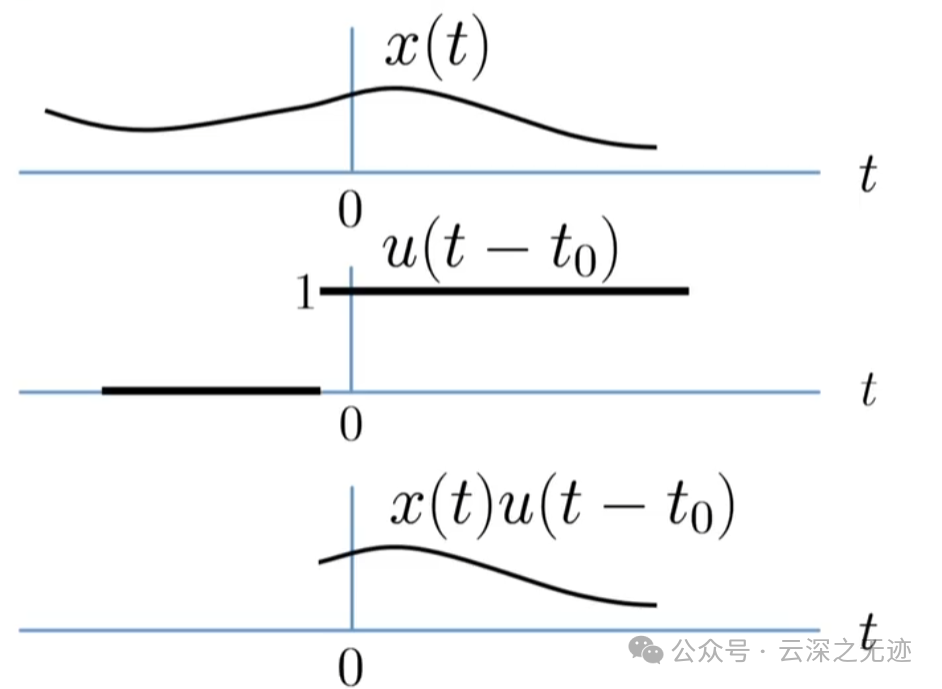
两个作用
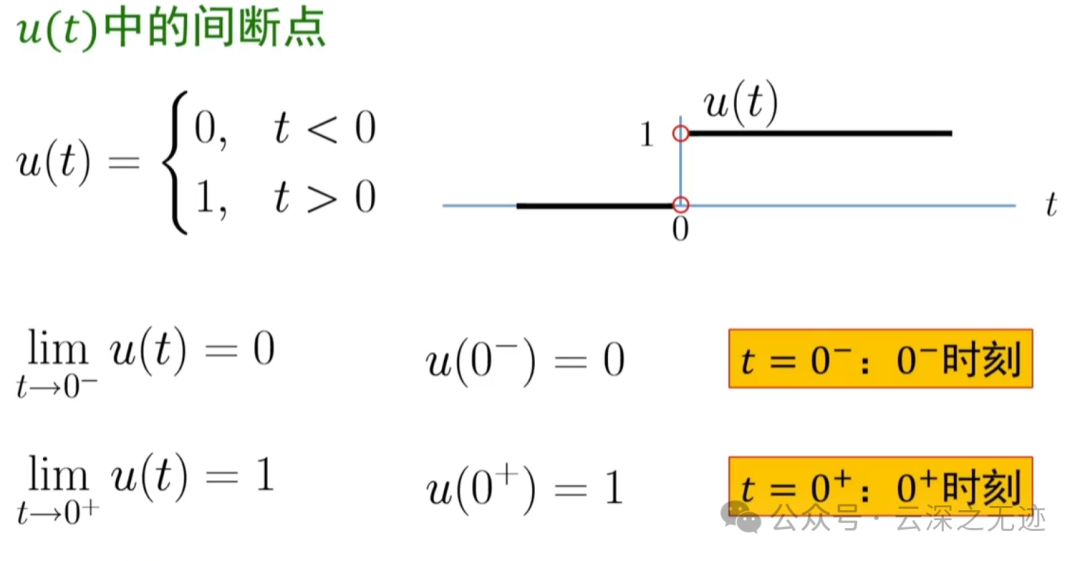
这个是我之前文章里面说的,0时刻分左右,0-里面蕴含能量,是0时刻
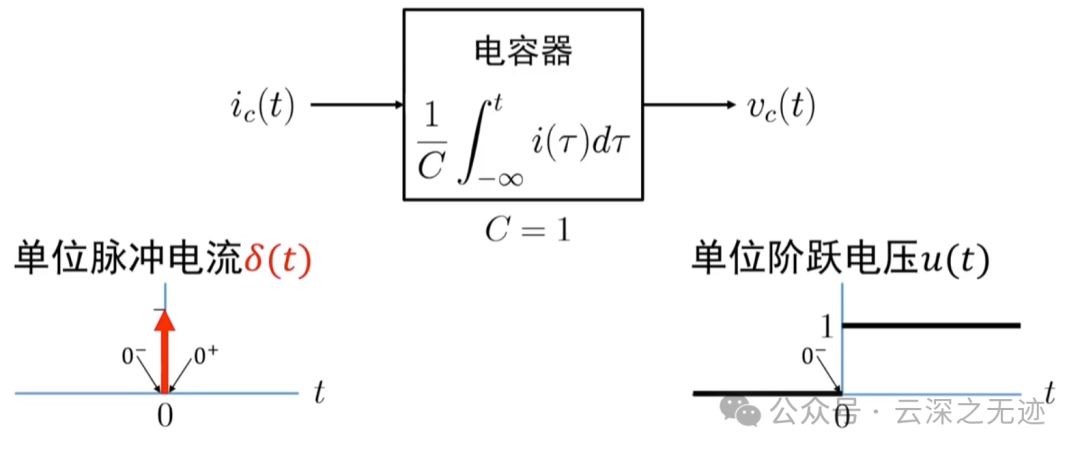
这样是不是就理解了
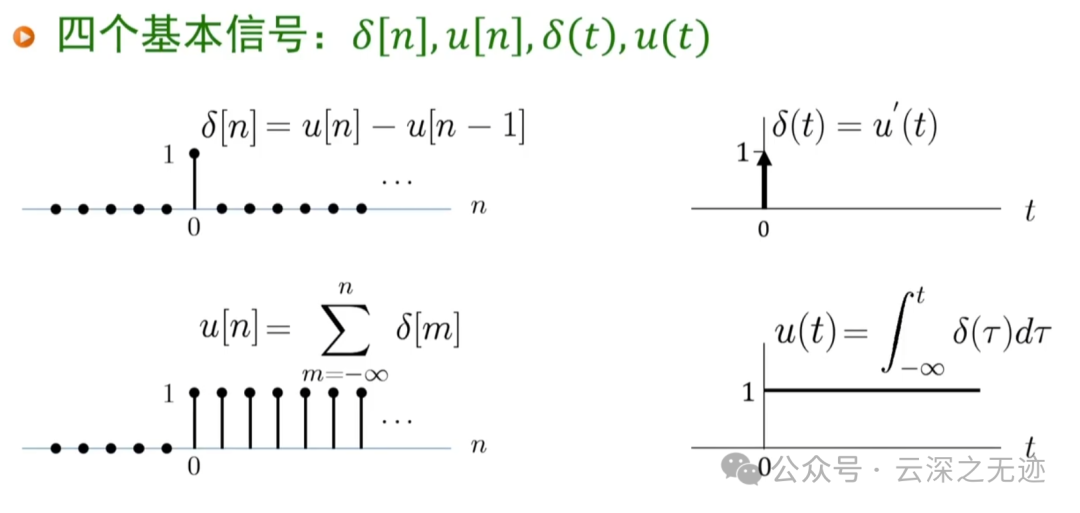
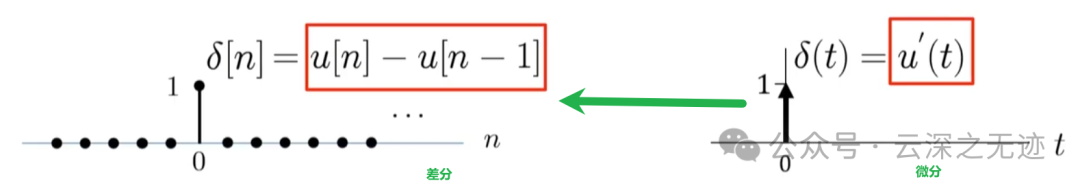

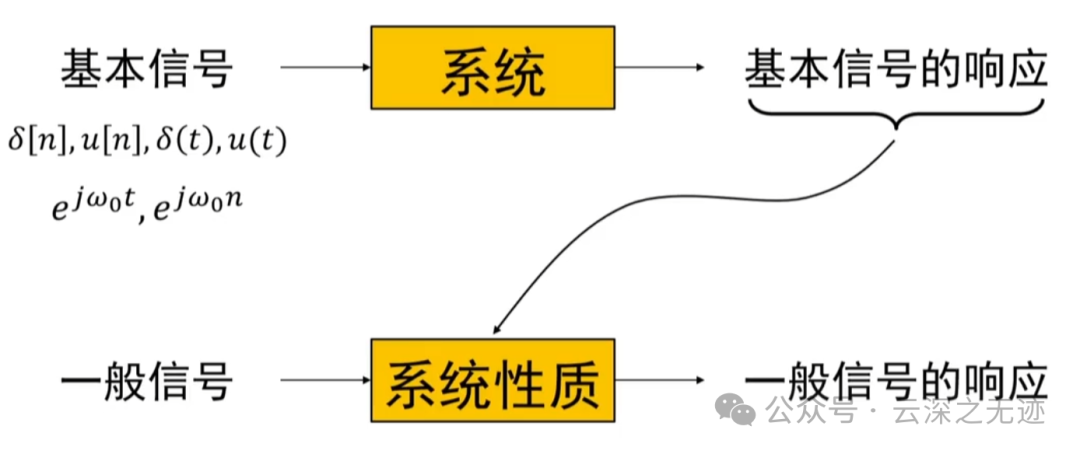
他是学明白了

1.5
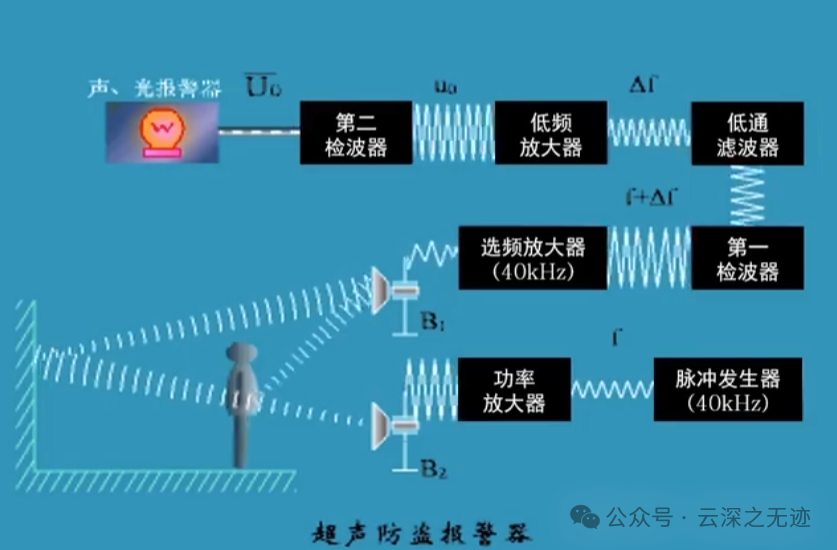








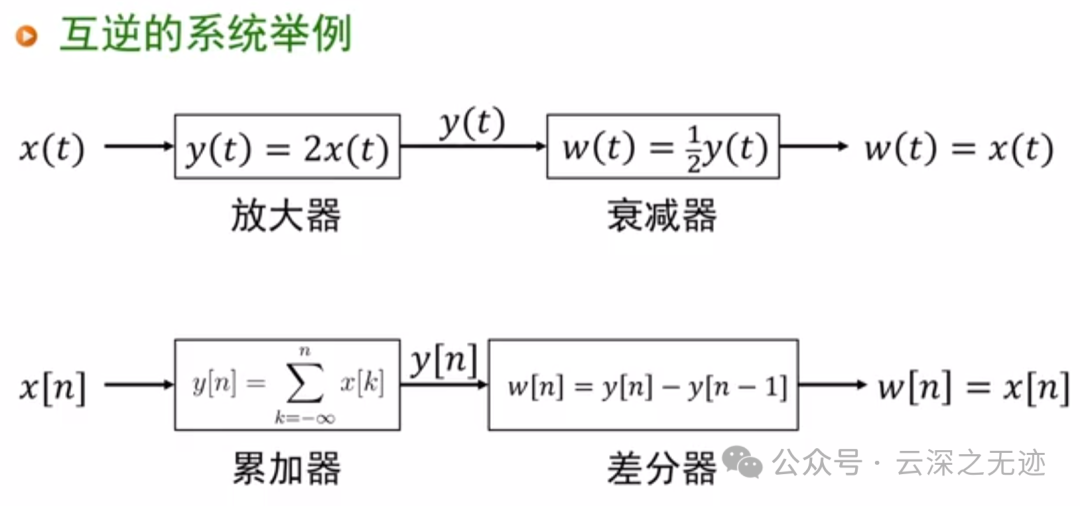




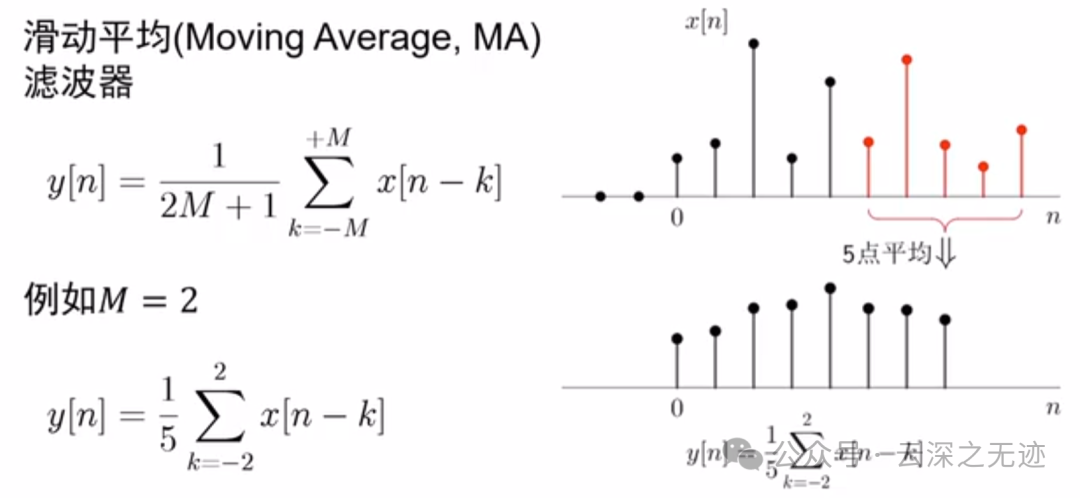






最后这个是限制定义域的作业
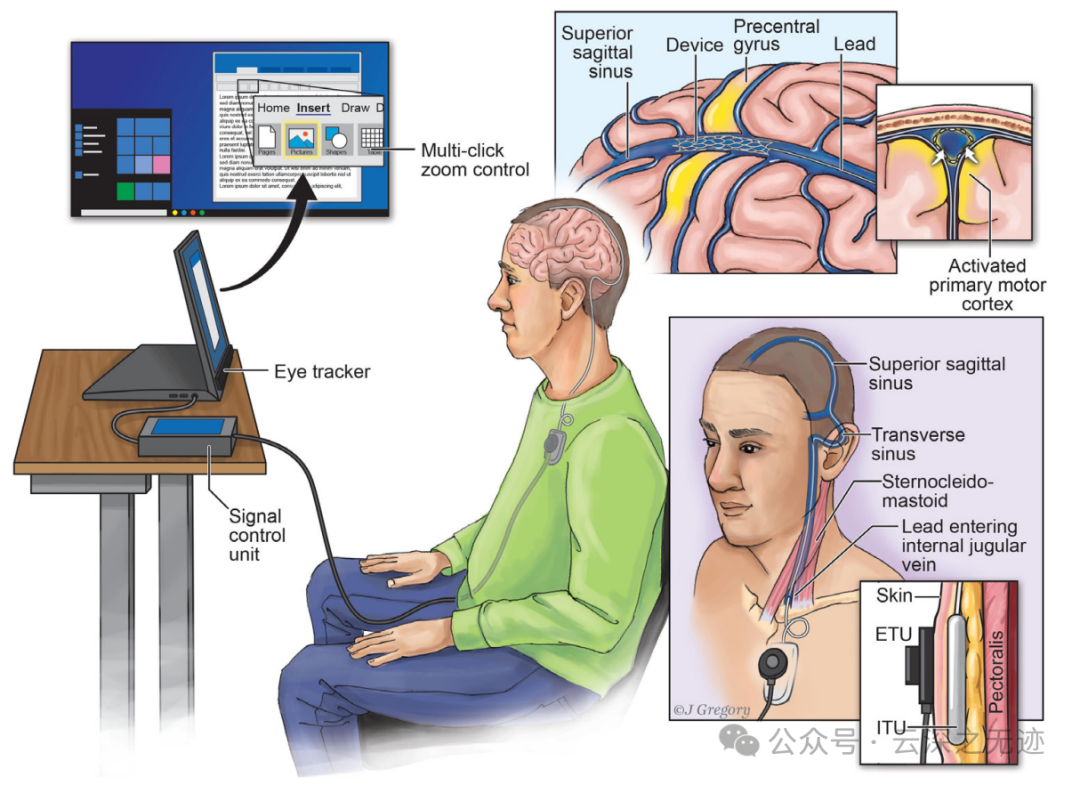
最近不是有 gpt 怼人脑子里面的感觉事情吗?这就是论文,我看了看👀,看看有什么不一样.