清华大学电子工程系李越副教授团队与自动化系戴琼海院士、吴嘉敏副教授团队合作,提出了一种用于微积分方程求解的模拟计算架构,基于逆向设计的超构材料结构操控电磁波传播,最终在亚波长尺度求解微积分方程(图1)。本研究提出的超构材料处理器具有小尺寸、高集成度、可重构的优势,为高速模拟计算的多功能扩展与高密度集成提供了可行方案。
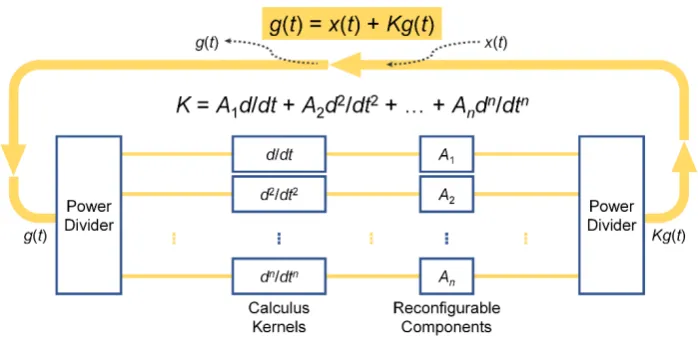
图1. 可重构超构材料处理器的基本架构。包含反馈回路、微积分内核、具有调幅调相功能的可重构元件等基本单元。
微积分方程的应用几乎涵盖了所有科学领域,例如天文学中的天体运动、生物学中的种群增长、以及电磁学中的麦克斯韦方程等。精确而快速地求解微积分方程可以帮助人们理解系统的变化规律,并预测其发展趋势。传统的微积分方程求解往往采用基于数字电路的数值分析方法。近年来,由于其高速率、大带宽、高并行度的优势,以电磁波为信息载体的模拟计算系统被广泛研究,为快速精确求解微积分方程提供了新思路。例如:宾夕法尼亚大学研究团队利用芝士形状的介质结构实现了特定积分方程的求解;瑞士联邦理工学院研究团队利用特定结构的拓扑特性成功求解了线性微分方程;而阿姆斯特丹大学研究团队基于周期排布的超表面在单元自由空间中实现了积分方程的求解。然而,现有的用于求解微积分方程的模拟计算系统仍然面临尺寸大、集成度差和可重构实现等诸多挑战。
针对该问题,本论文提出了基于超构材料的新型可重构方程求解架构。如图1所示,该架构主要包括反馈回路和执行微积分运算的可重构超构材料内核。图2展示了所提出的像素超构材料的基本结构,通过逆向设计像素超构材料微小单元之间的通断状态,可以亚波长尺度上精确操控电磁波,最终实现任意阶次微积分所需要的K(ω) = [j(ω - ω0)]n运算内核。而反馈回路控制微积分超构材料内核两侧的电磁波信号完全相同,即g(t) = x(t) + Kg(t),实现了方程等式的构建与求解。进一步地,通过调控可重构元件,可以进行不同系数、不同阶数的微积分运算,构造不同的方程求解器内核K,实现任意的线性微积分方程。如图3所示,基于该架构,在微波频段下设计了尺寸仅为0.93λ0 × 0.93λ0的超构材料处理器样机,并实验证明了该处理器能够在亚波长尺度实时求解任意的线性微积分方程。而在现有文献报道的求解微积分方程工作中,至少需要38.70λ0 × 77.40λ0的面积来实现一阶微分方程求解。与此同时,受益于超构材料处理器的亚波长尺寸,该处理器可在30个运算周期内实现快速微积分方程求解,是现有文献报道的最少运算周期数。本论文所提出的基于超构材料的微积分方程求解器在亚波长尺度实现了系数可调与方程阶数可扩展,具有集成度高、求解速度快的优势,在实现高密度集成多功能可重构模拟计算方面具有较大应用潜力,为理解和预测复杂实际系统的动态趋势提供了新方法。
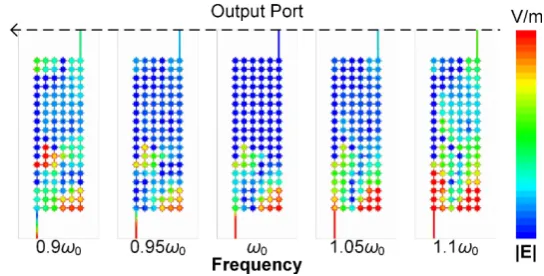
图2. 基于逆向设计像素超构材料的一阶微分内核,以及其在不同频率下的表面电场分布。
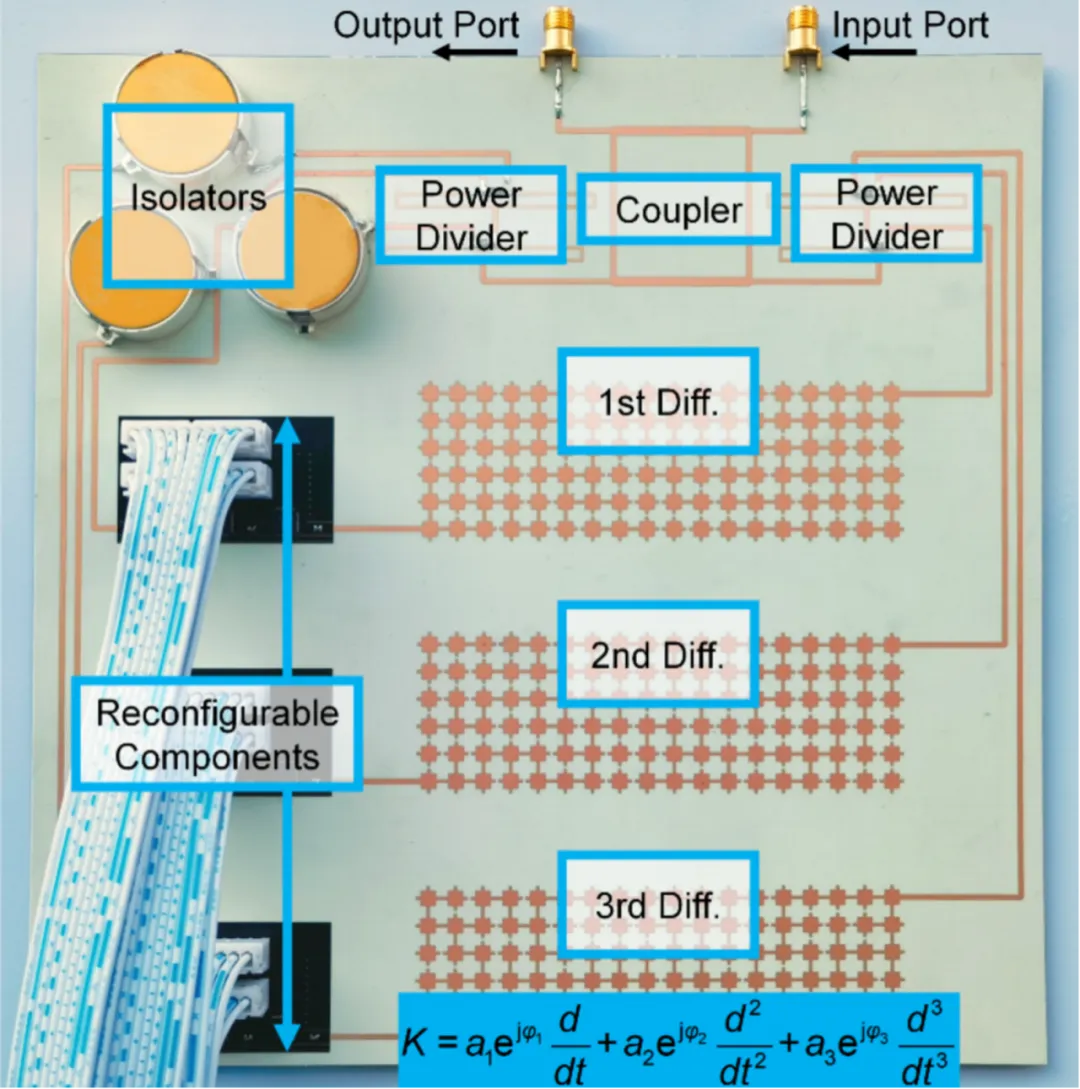
图3. 可重构超构材料处理器的实物图。
近日,该研究成果在《自然·通讯》(Nature Communications)期刊以题为“求解任意线性微积分方程的可重构超构材料处理器”(Reconfigurable metamaterial processing units that solve arbitrary linear calculus equations)的发表。论文本论文的理论和实验工作均在清华大学完成,清华大学电子工程系为论文第一单位。电子工程系李越副教授、自动化系戴琼海院士、吴嘉敏副教授为本文的通讯作者,电子工程系2021级博士生付鹏宇为本文的第一作者,其他作者包括电子工程系2017级本科毕业生许梓萌与电子工程系博士后周天贶(清华大学水木学者)。本研究得到了国家自然科学基金(U22B2016,62088102,62222508)和北京信息科学与技术国家研究中心光电智能计算交叉创新群体和电子工程系自主科研项目的资助。
文章链接:
https://www.nature.com/articles/s41467-024-50483-x

