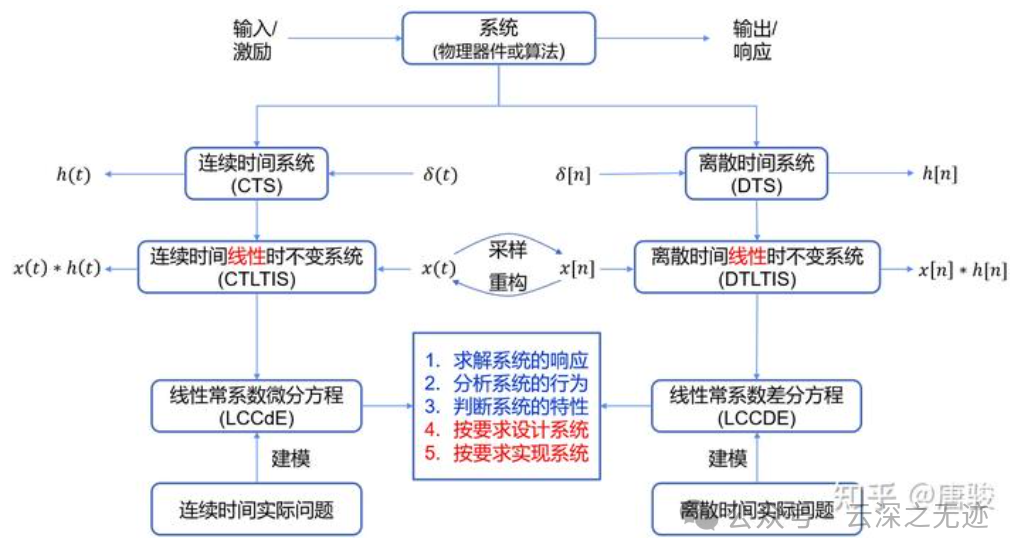
唐老师的图是最好的:
一般函数使用n个正交函数的线性组合来表示:
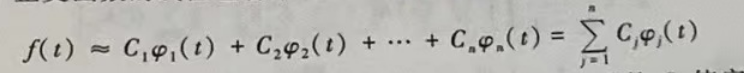
C就是里面的系数

因为只是可以用无穷项的函数项级数来逼近,肯定要遇到收敛的问题,多少项就满足误差了,以及误差如何度量。
这里使用了均方误差 (MSE)通过最大似然MLE推出来的最小无偏估计:
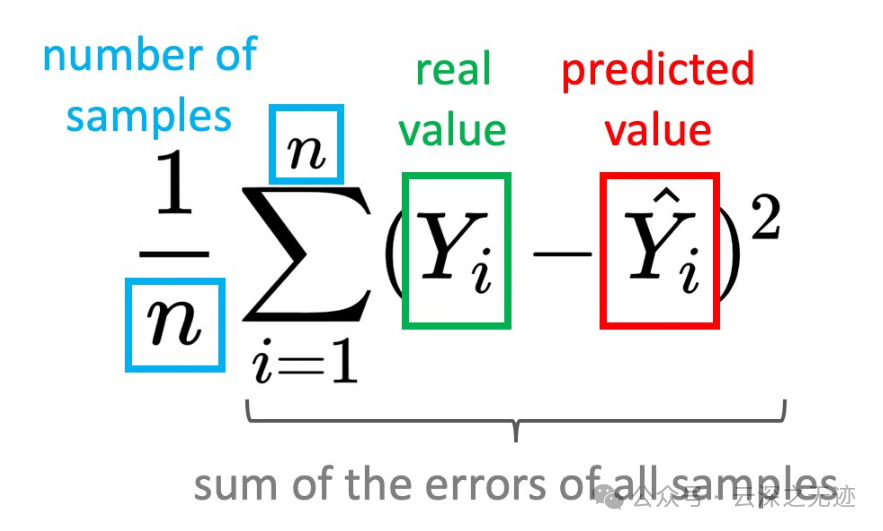
最好的解释就是这样!

至于为什么是平方,是因为里面的两项之间有正有负
方差的公式和这个差不多:
两个的计算公式比较相似,但是统计意义差别很大,一般来说,方差是计算一组数本身的离散程度,而所谓离散,是指每个数据和本组数据的平均值的距离(即差值),因此,方差越大,表示数据本身的离散程度越大。
但是均方误差处理的是回归模型对因变量的预测值,和实际观测的因变量数值的差异,数值大,意味着预测的值越不准确(因为预测值距离观测到的数值很远),表示回归模型不是很靠谱。

这是西瓜书上面的,确实是作为性能度量出现的
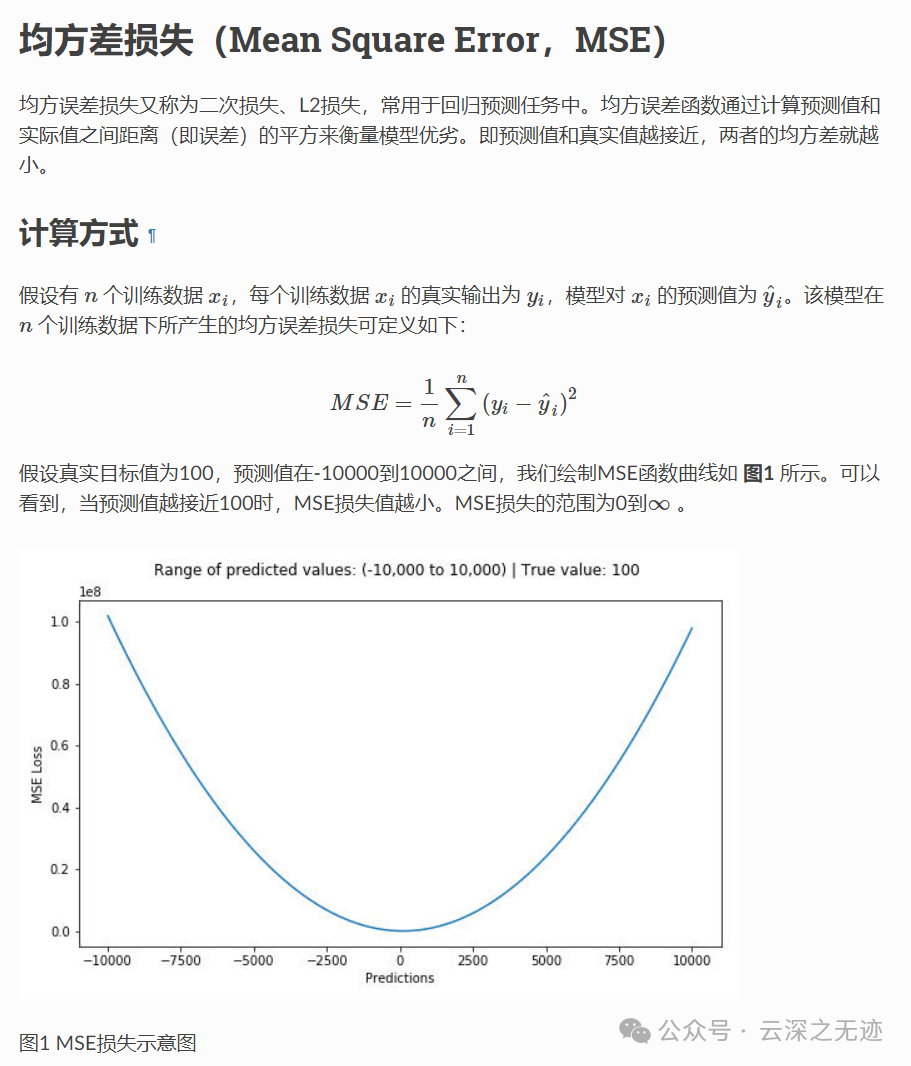
另外,飞桨也说了一下
反正公式就是这样的:
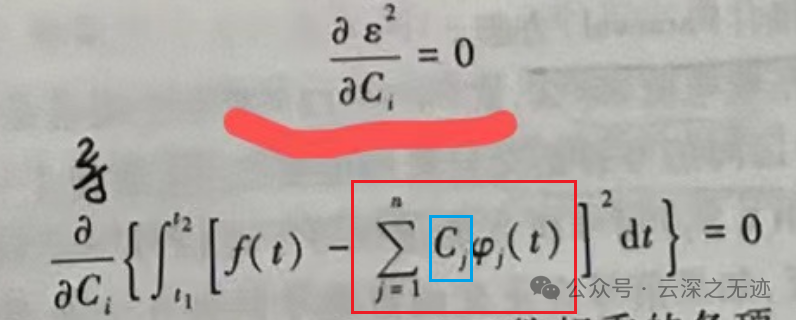
也就是说要想这个公式成立,f固定了,看后面这一项,正交函数集动不了,只能看系数,事实上也就是只能看看系数。因此就是对C求偏导。
啊这,早知道不问了

我还有一个大的
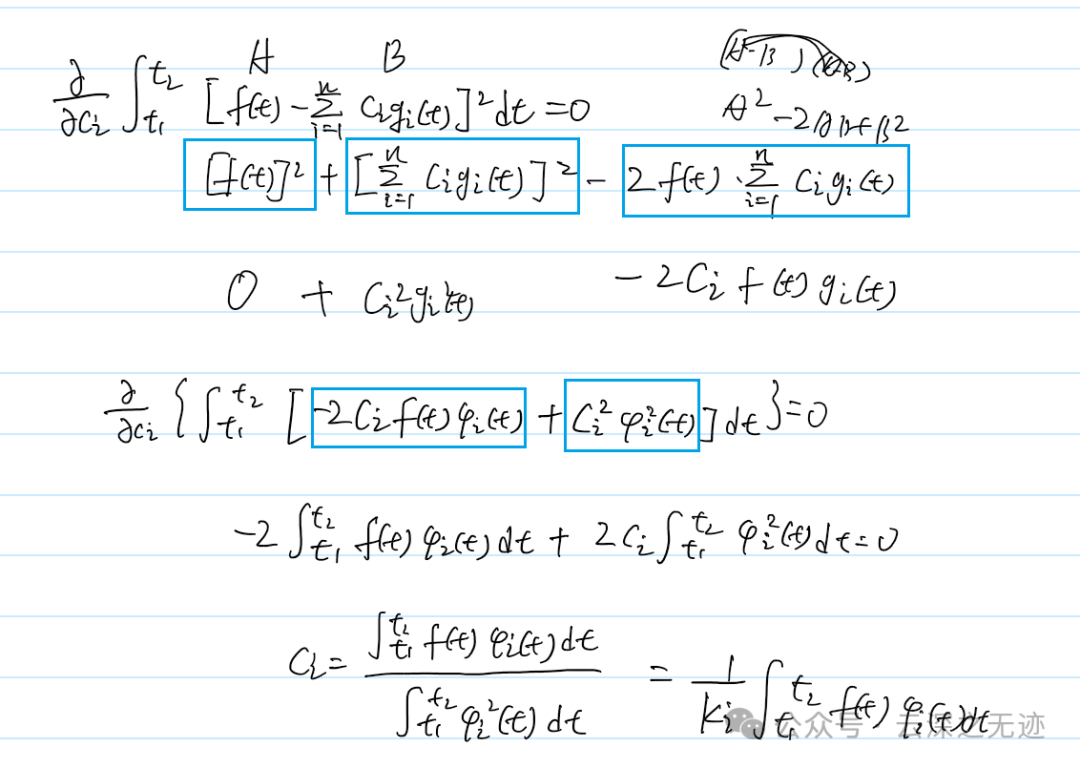
好丑的字,其实就是两项展开
序号不同的正交函数相乘的各项,积分为0,要的就是效果。不含Cj的项对Cj求导也是0,因为求偏导,其他项看上去是常数就没了。
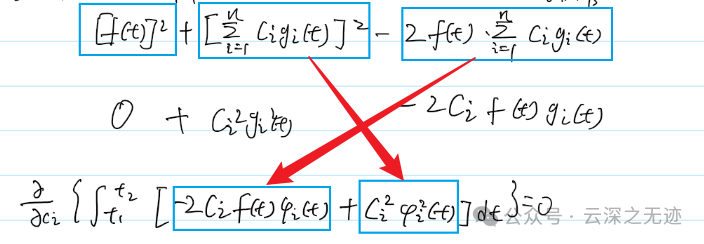
重新排列
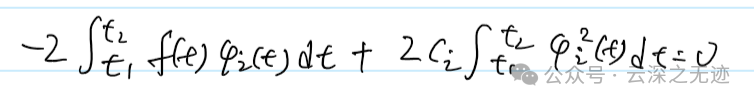
求导,定积分的性质用起来
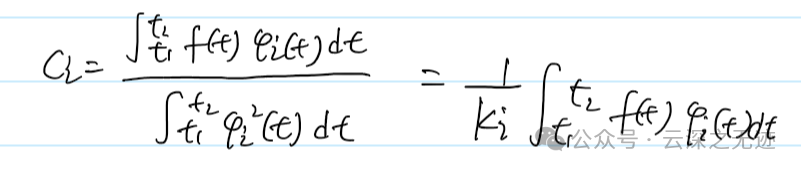
重新移动,这个Cj就出来了,这就是系数
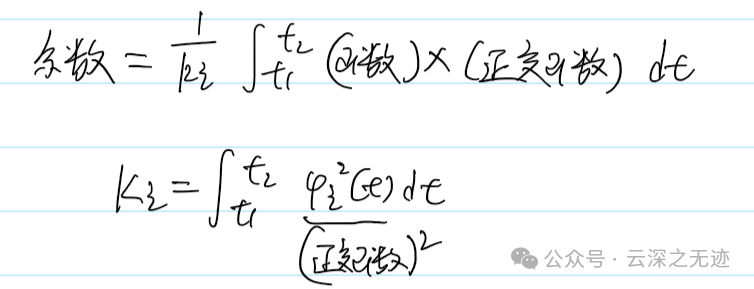
也就是这个样子的表示

最后把我们的系数倒进去,看看效果,Cj,Kj两个系数,接着就是到最后一步了。

这玩意儿又叫帕塞瓦尔,能量守恒

这个是一本书上面的定义,Cj也叫傅里叶级数的系数
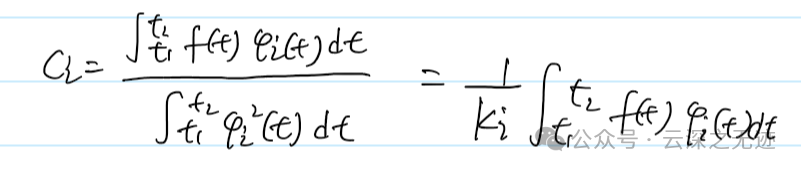
就是我写的这个东西,里面的Ki
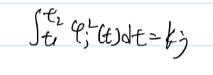
就是函数集的绝对可积
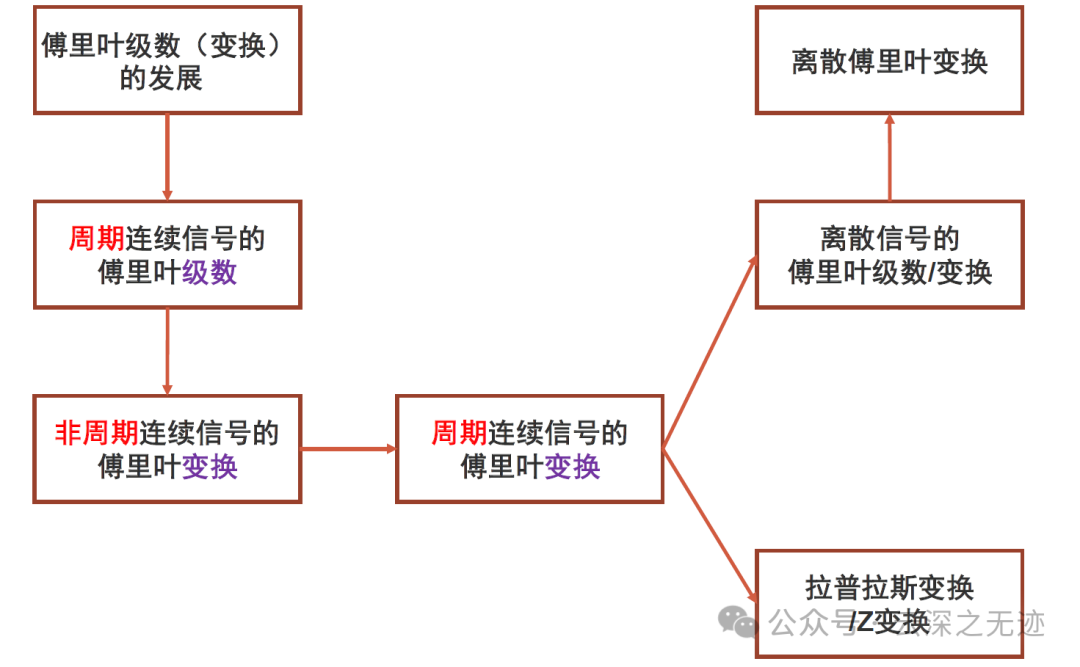
然后傅里叶级数是频域分析的大头
我们的工作还没有完,甚至说,我们的正交函数还没有用到。
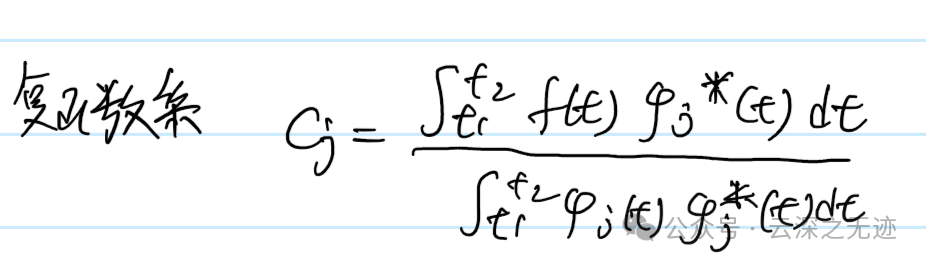
我们可以先看一个使用复函数来分解的例子
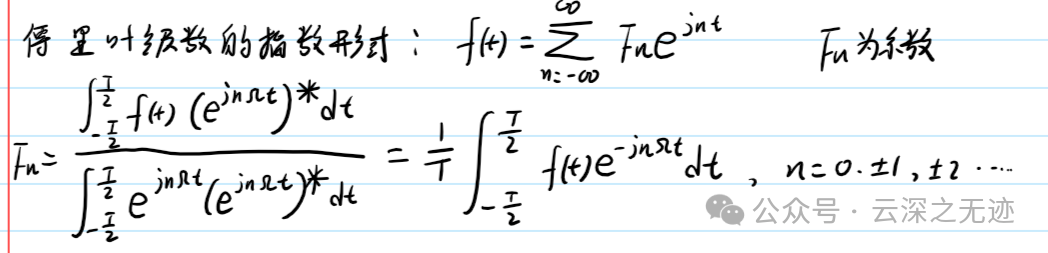
我字好丑,这里使用了共轭
挺无语的,傅里叶级数都在高数里面扫尾了,那我走?
所有函数构成函数空间,取一些基本的、正交的函数,再定义组合规则。每个具体领域,加法和乘法的含义有所不同。对于函数,类似于乘法的概念是积分。两函数的正交,就是相乘后积分为 0。当 f(x)、t(x) 作为基本函数,这样 k(x) 用两个函数叠加的方式来表示。
k(x) = a f(x) + b t(x)
这时需要求出系数 a 和 b 的。可以两边先乘以 f(x), 得出,
k(x) * f(x) = a f(x) * f(x) + b t(x) * f(x)当 f(x) 和 t(x) 正交,两边取积分,就可以消去,t(x) * f(x)。这样系数 a 就只会跟 k(x) 和 f(x) 有关系。
k(x) * f(x) = a f(x) * f(x)还可以有多个函数相互正交,甚至无限多个函数正交。比如选取 cos、sin,作为基本函数,叠加起来表示其它函数,就演变成了傅里叶变换。

牛逼
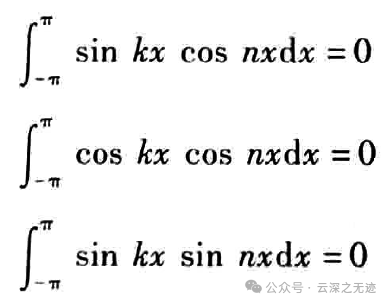
持续牛逼

但是是相同的时候是Π
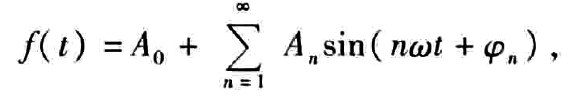
反正正弦函数表示的级数是这样的,不知道你有没有奇怪,为什么突然出现了一个A0,这里书上说一般是直流分量,即使是没有任何应用背景的高数书也是这样写的。
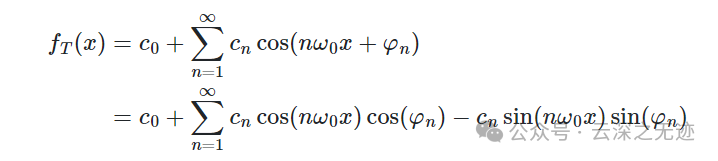
这里,那个展开都可以
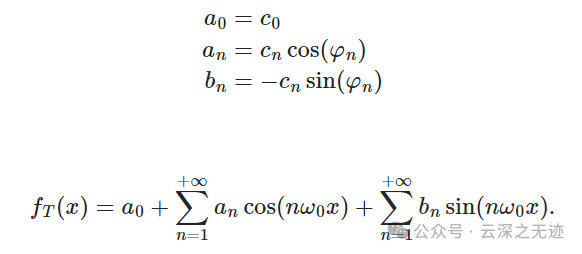
这里是COS打开的,教科书是SIN
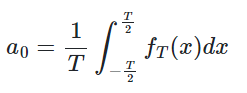
这里积分,a0是这个值

把级数打开,给里面的项重新写一下

a0的求法是俩边积分,就出来了,原函数积分一次用Π除

同样的操作把所有的系数都求出来
这里需要知道一点的就是a0,这个值很怪,为什么是二分之一?
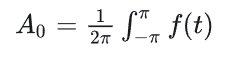
这个是A0

因为A0的系数分母是2Π,为了整齐,提前设置为a0=2A0
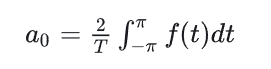
大概就是这样吧。。。我都有点糊涂了。a0就是f(t)函数的平均值
所有的向量构成一个空间,而所有的向量是无穷无尽的。一个个向量分别分析也自然没有尽头。这样我们挑选几个相互独立的基本向量,再定义一套组合规则。这样其它的向量,就用基本向量组合起来表示。
于是很自然地产生问题,基本向量是什么?如何才叫相互独立?组合规则是什么?
对于向量空间,组合规则其实就是线性叠加。乘法和加法很基本,不同的领域常常会重新定义类似乘法的概念和类似加法的概念。在线性叠加中,类似乘法的概念,就是向量的内积,当内积为 0 表示两个向量相互独立。
假设 A、B 为基本向量,C 可以用 A、B 叠加起来表示。于是
C = a * A + b * B两边乘以 B,得到C * B = a * A * B + b * B * B
这里的乘法符号其实是内积,假如 A * B = 0,就可以消去第一项,系数 b 就只和 C 和 B 有关。而当 B * B = 1 时,可以再次简化计算过程。
当将二维向量几何化后,内积为 0,两个向量刚好正交(orthogonal)。另外一个术语就是平行,跟正交对应。平行表示完全相关,正交表示完全不相关,有时会处于平行是正交之间,它们的夹角可以表示相关程度。
当 A * B = 0 ,A、B 正交;B * B = 1,B 标准化,也叫归一化。当正交归一的向量,作为独立的基本向量,线性叠加成其它向量。会使得计算过程大大简化。

这个是复数形式的系数推导,电子书我没有看到
https://zhuanlan.zhihu.com/p/435515042?utm_medium=social&utm_psn=1801584997649502210&utm_source=wechat_sessionhttps://www.amazon.com/Signals-systems-transforms-James-Cadzow/dp/0138095426https://www.cnblogs.com/clemente/p/11301180.html