你很着急,但知识不着急
我说的

你选择了学习,就慢下来学懂它
我爱信号处理,这东西太骚了。
我们打交道的就是时域空间,连续不间断的信号,电脑处理的是连续孤立的点。咋办咋办啊!
OK,连着是吧?都别活,想办法打撒就行了,怎么打?使用单位冲激,事实上这个是一个理想的概念,就是一个函数,这个函数是这样定义的:

这个样子的
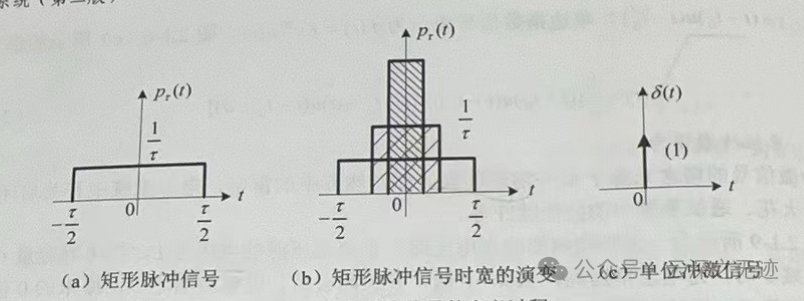
就是我们把时间缩短,但是面积不变,自然而然的就出现了这样冲天线的东西。

然后呢,就是考虑这个信号的一些直观性质
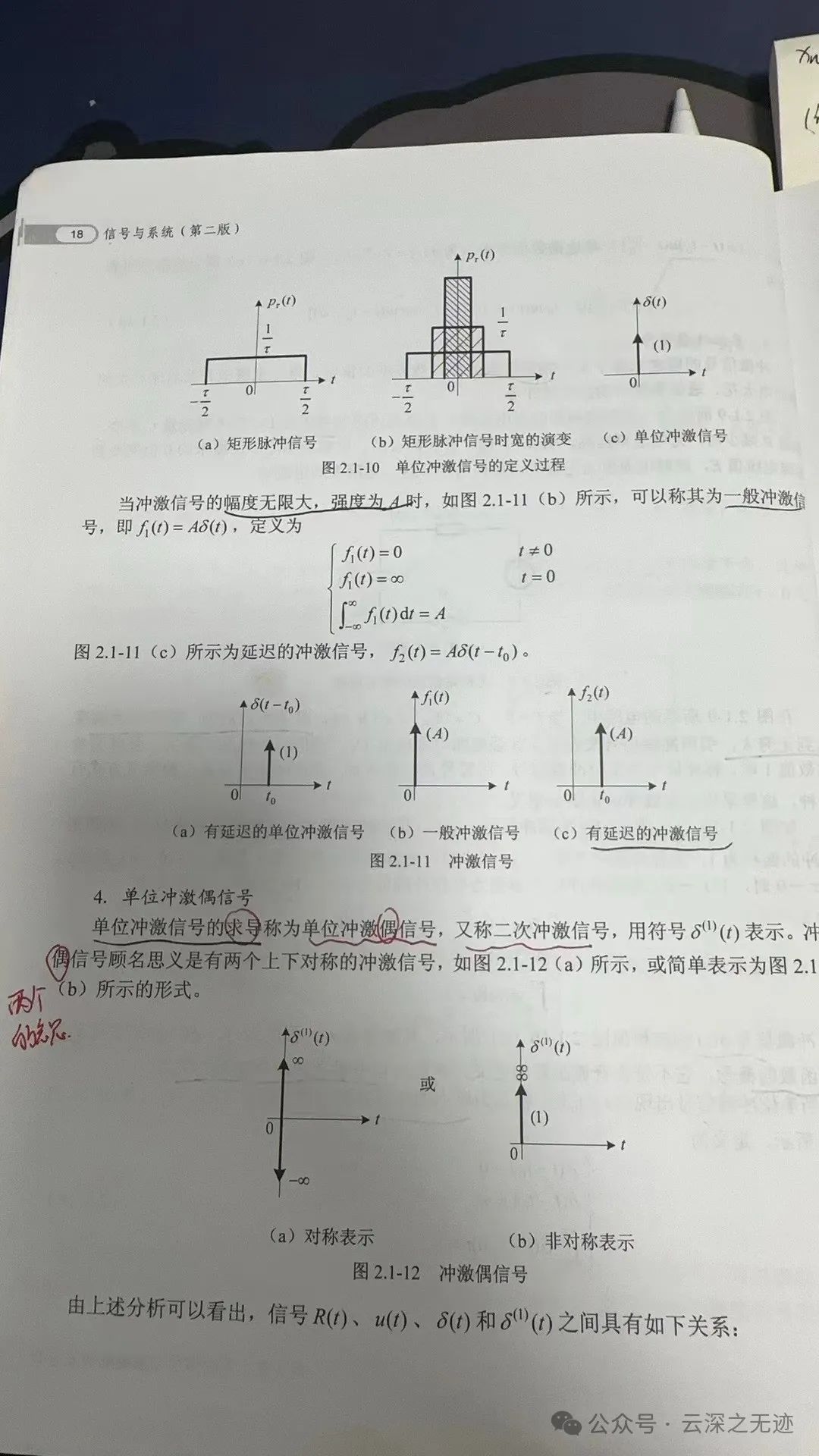
一直看书里面都说冲激偶,终于明白了
这本书是职校的书,我有天搞到半份PDF,看的津津有味,后来费老鼻子劲儿才搞了本二手的。怎么说呢,职校的东西就真的说的很明白。咱们也不知道正经教材是不是怕我学会。

我这里不说这个东西咋来的,在信号系统是通过单位阶跃信号来的,然后还有一种是单位斜变信号,两个东西的关系就这样:

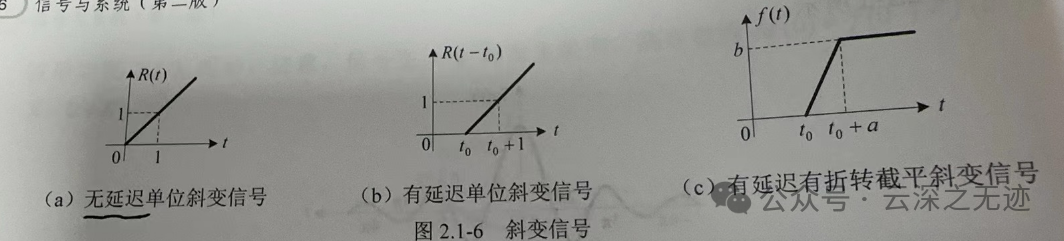
生活中最多的,就是这样的信号,一开始没有,然后慢慢增长,最后平稳
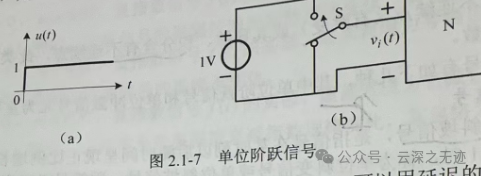
然后我们考虑的极端点,没有这种缓慢的增长过程,直上直下,这里就使用开关模拟,这里就不得说单片机的按钮了,如果这么理想就不需要20ms的延迟读取了。

接下来就是加了延迟,为什么?因为大多数时候不是0时刻执行的,对于这个东西无所谓,因为距离和空间都是相对的。
OK,这里其实讲的是一种开关的状态,如果我们考虑效果呢?比如给一个电容充电,这一瞬间让我想起来了刘慈欣的小说,全频道阻塞里面一个电子的感受。总之就是一瞬间,电流的强度非常大。SO?你看,瞬间,就算光速吧?然后电流很大,为啥?因为是时间很小了,一个分式就很大了。也就是信号的幅度很大。我们把强度定位在1的时候称为单位冲激。
现在想冲激信号是不是就合情合理了。
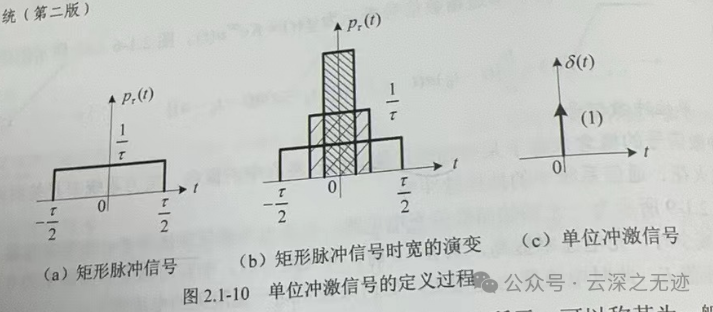
那这个矩形信号的意思就是:最左边,哥来了!,然后持续一段时间,最右边,哥走了!
我认为闭合,就是说明了一次完整的冲激过程,上面说了时间脉冲是短的!!!极限就是时间为0(lim登场),就变成了单位冲激信号。
上面这个信号好像一个门,也叫门函数,可以使用两个阶跃信号来组成,一边一个。
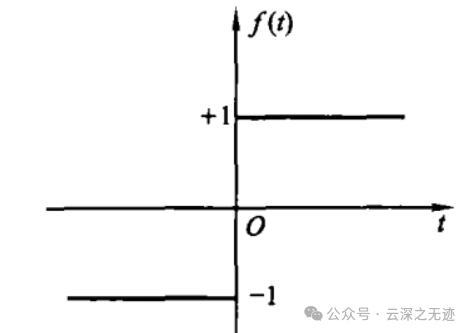
这个叫做符号函数,也可以上面的阶跃信号构成,就好像搭积木一样
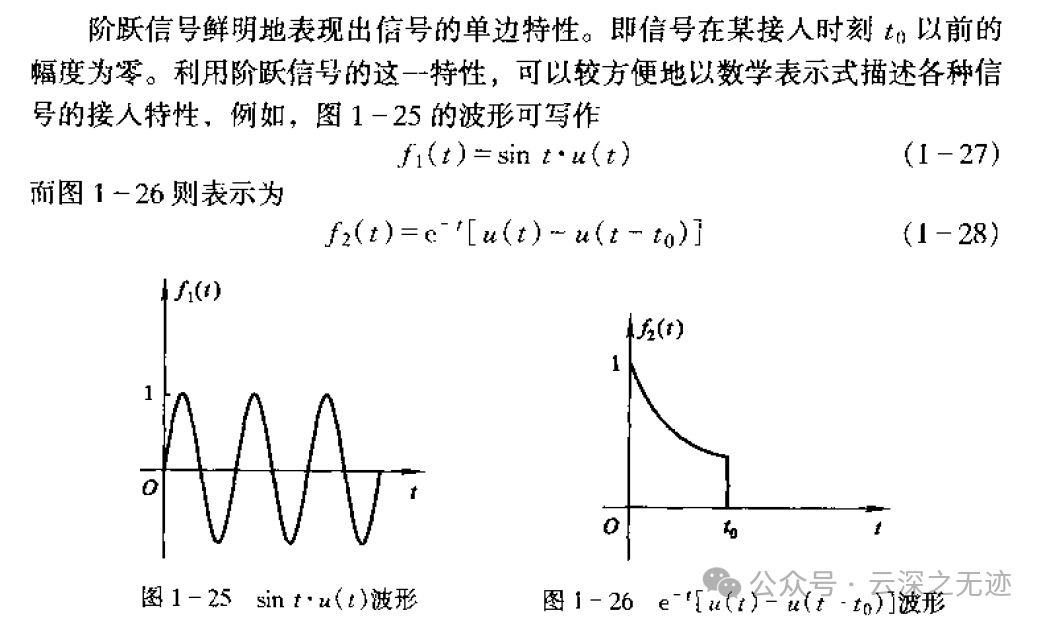
这段写的(๑•̀ㅂ•́)و✧,赞
用词考究而装逼,好喜欢,接入特性~
信号微分得到的是冲激信号,这个也好理解,微分是线性近似,求的是值,冲激信号重要的也是幅值。强度=跳变值。
信号呢,可以分解为,直流和交流两种。
这里我说一个例子:
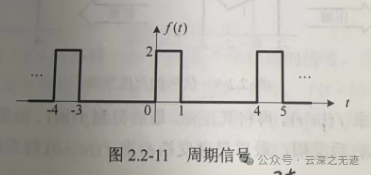
你看这个方方的波,问你直流是多少
我第一次看这个东西,是懵逼的???啥?什么直的
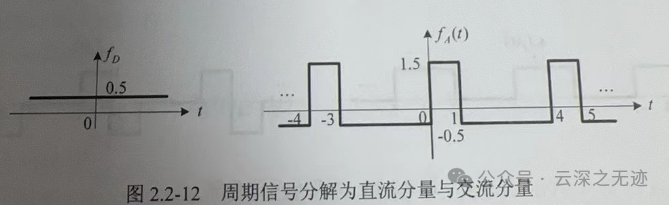
事实上,通过定义,求这个时间的均值确实是可以算出来的
我后来反思,可能是因为平时很电子打交道对,先入为主的认为,直流信号就是直的(我不知道在说什么了,希望你懂)

对!还有一个信号可以分为偶和🐔信号,妈的,也不说信号与系统了,高中,大学这个东西没少让你算吧?任意一个函数都可以分解为🐔和偶函数的和。事实上,它的内涵非常的深厚,比如🐔函数天然的告诉你f(0)=0直接就是一个中值定理的条件,然后还有积分画图什么的,以及后面的傅里叶级数:

希望都是🐔函数,都为0,偶函数嘛,滚
害,知识就是这样,铁板一块,我说单独的讲这个单位冲激串吧,确实还总结说不出来,所以就补了这么多的内容。
接下来就可以说单位冲激串了!
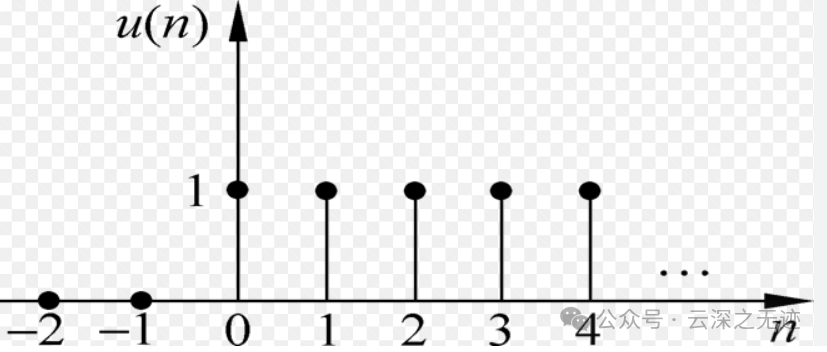
它是这样
然后和一个连续的函数一乘,因为这个函数的定义域有个限制:
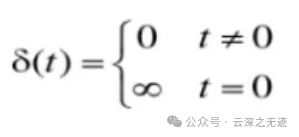
也就是说,只有0的时候才是有值的,除此之外都没有了
有冲激的地方就有值,这个强度呢就是时序函数f(t)这点的幅值,就是函数值把这个冲激带到更高的地方,没有冲激就为0.
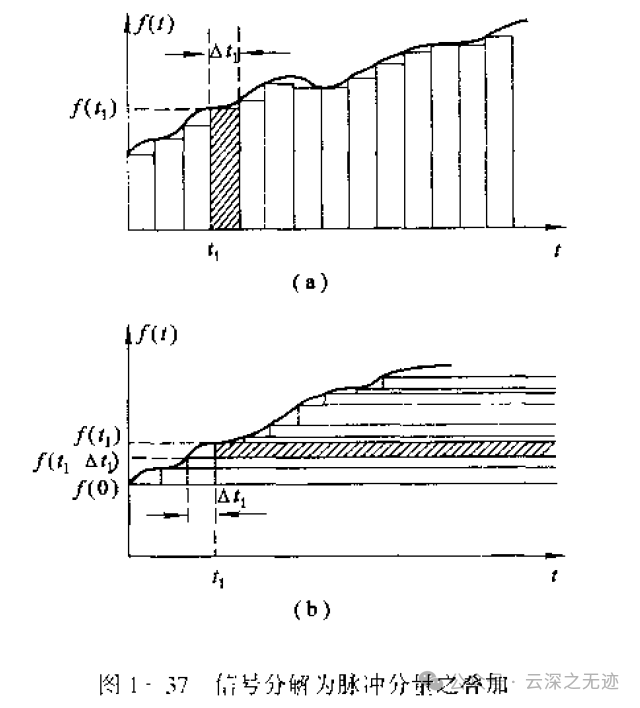
也就是说,信号可以有两种方式,第一种是冲激信号的叠加,一根根的小线顶起来,还有一种是台阶信号的叠加,看见b图飘逸的长发了吗?
现在一个连续的信号就变成了一个冲激强度了。那么这段冲激信号的包络线就是原来的函数,这就是采样过程。
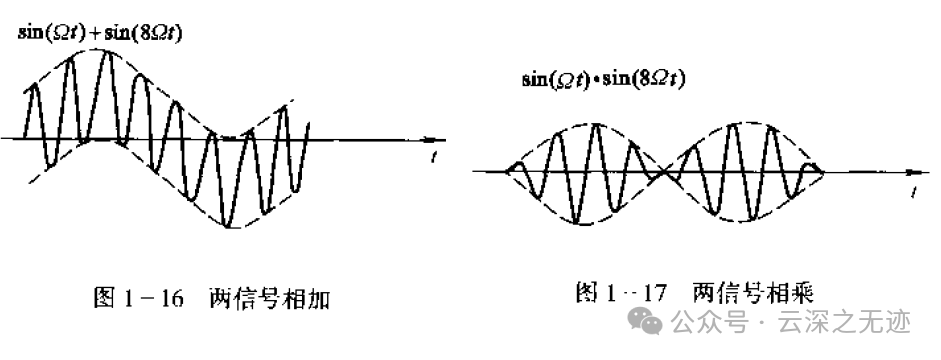
包络就是外面这层的样子
等等!这个东西打碎以后还是原来的东西不?

小伙子不错哦!还能问出这么骚的好问题

先知道什么叫采样率,就字面意思
奈奎斯特频率(英语:Nyquist frequency)是离散信号系统采样频率的一半。
采样定理指出,只要离散系统的奈奎斯特频率高于被采样信号的最高频率或带宽,就可以避免混叠现象。
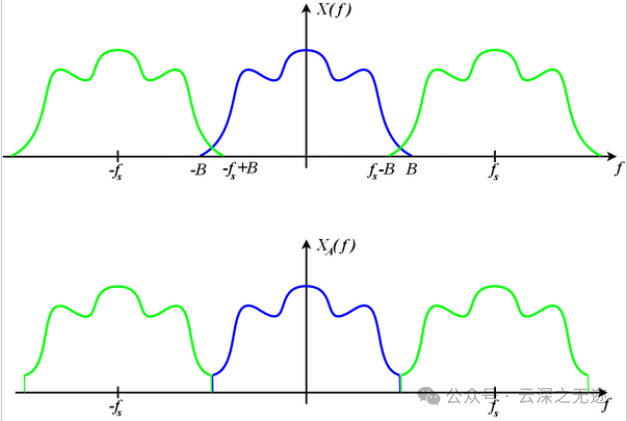
这个图就挺好的,你看这个上面,交叉的一些值,这个就是在时域混叠
混叠这个名字挺好的,混是感兴趣的分量分不开,叠是咋混的:

大概就是这样叠的,哈哈哈哈
真的,你就学会这个出去装逼就行,但是吧,二倍在现实中远远不够。

这里就从这本书里面翻吧,大家东西都一样
教材里面一般会有LTI的微分方程描述什么的,哥,先不整这个。
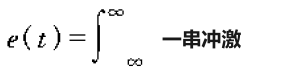
上面我们的离散工作就可以写成这样
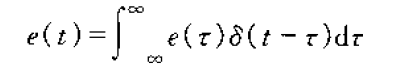
这里我们就可以写成这样,任意信号都可以使用冲激信号的组合来表示。
你看这个e其实就是我们要分解的函数,后面这个就会冲激函数,里面有个t在干什么?
还记得上面函数的定义吗?除了0之外的地方就没有值了,所以这个t就平移和挪地方用的,写成f(nT)Q(t-nT)可能更好看一些。每有一个T,f函数有一个值,这个Q也是把0点处的强度移到T位置。
hhhh,不好意思了,我其实写文章是写写Z变换的,没想到才写到卷积。我要不开始Z变换?日后擦个屁股?
OK,愉快的决定了。
什么是Z变换?好问题,你知道什么是拉普拉斯变换吗?怪不得教材要这样设计,没想到我写个文章都跳不了。
傅里叶有两种,一种是级数,一种是变换。级数是针对周期满足收敛条件的变换(有4条,就是说明哪些函数可以被分解)
在形式上面有三角和复数两种,下面是复数形式(我以后补个傅里叶)
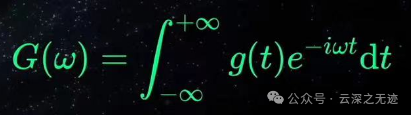
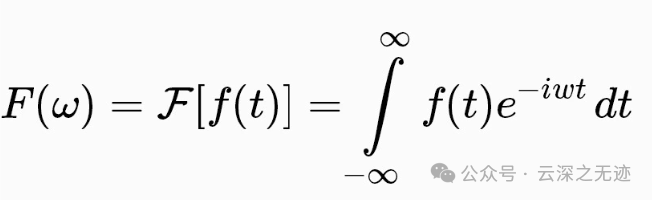
就是这样,这个叫傅里叶变换
这个傅里叶变换虽然好用,但是有很多函数分解不了,这些函数普遍都是很“勇”

就是增长太快辣!
比如,f(x)= x,f(x) = x^2,这些,那指数函数就别说了,早他妈看不见了。你说是这么牛逼的工具连这么简单的函数都搞不定?是的,就这么个情况。
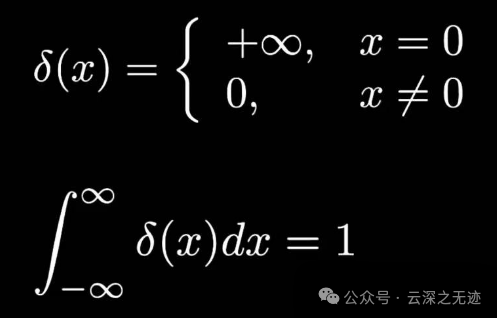
后来傅里叶就想了这样一个函数,情况好了一些
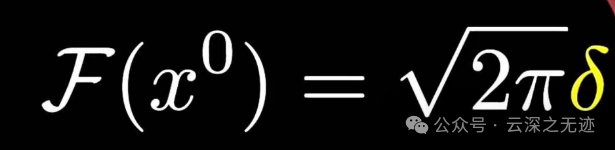
比如x的0次方就可以解了,就是带了这样奇怪的函数
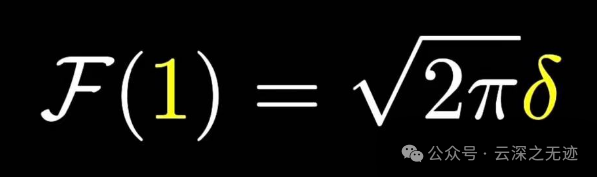
单位傅里叶变换
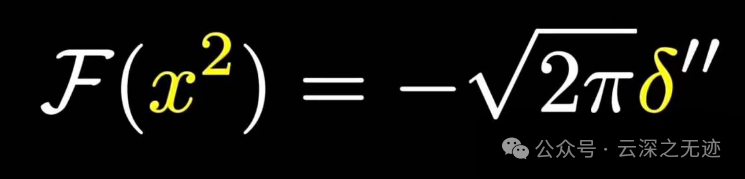
上面的x^2也可以解了
不过。。。看起来不好看,也不直观,哪个年代大家都说不出来这个奇奇怪怪的函数是什么。
拉普拉斯方程听说过没有?没听过也不耽误晚上吃饭:

大哥大概就这样吧
这个变换在现代称为积分变换,以前我不知道。拉普拉斯看了这个函数以后就想,emmmmm,既然是增长太快,可以想办法把它衰减下来。至于为什么是e这样一坨,我还没有研究。
核心思想就是,可以把疯狂增长的函数衰减下来继续傅里叶。
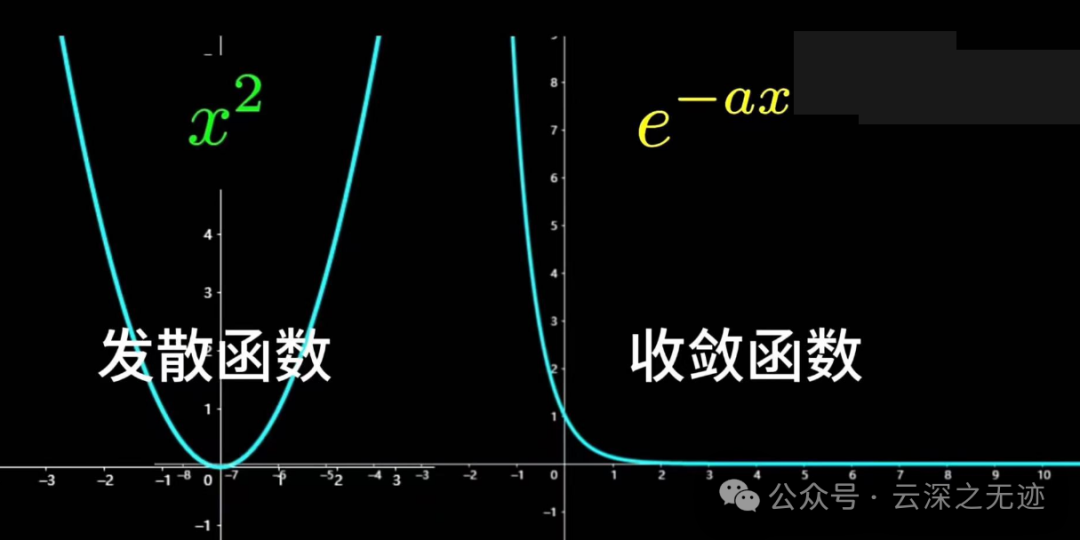
可以看到右边衰减速度很快
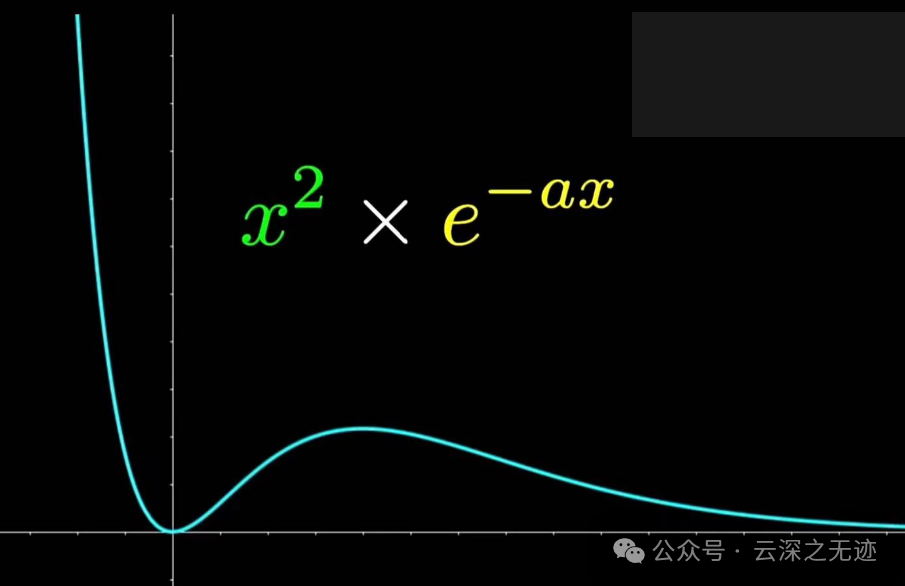
一乘,安排上了,别说衰减了,我感觉这函数都快死球了,无穷时候肯定贴地了。注意这里的区间,是0~+♾️。
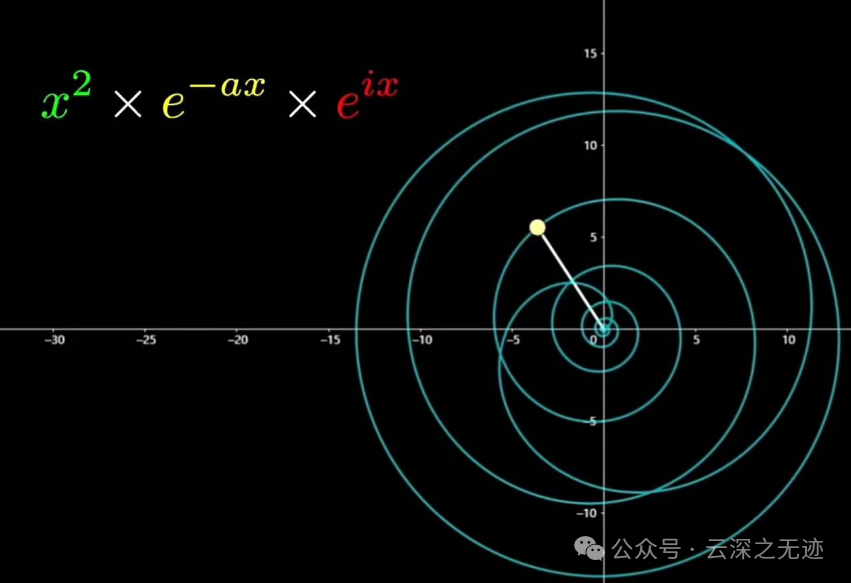
继续傅里叶变换,不错哦!我这里没截图,没衰以前是个螺线
嗯,不错,不错,有搞头!

然后把这个右面的欧拉旋转盘的旋转频率调整到和衰减系数一样
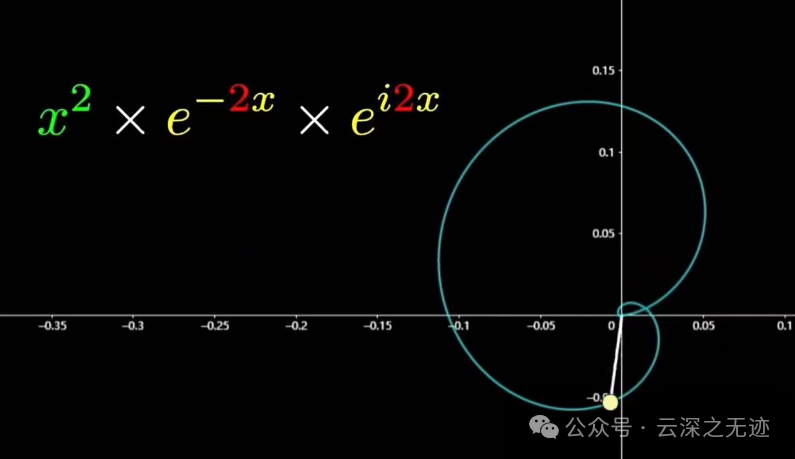
直接END,就出现了梦寐以求的单瓣图
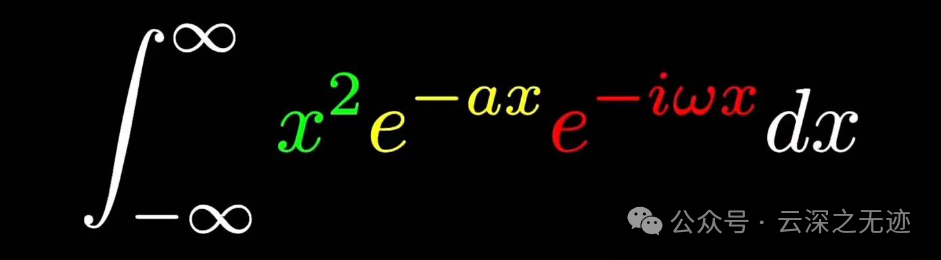
来化解一下
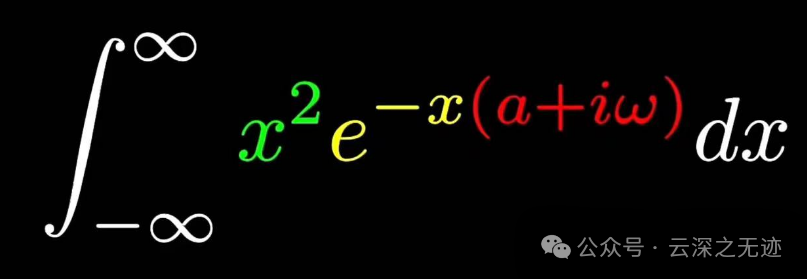
你看这个红色部分,老演员了
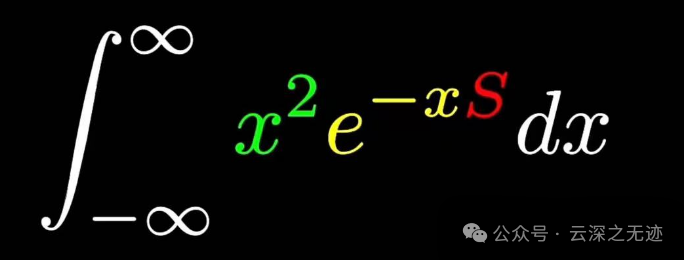
我们给它搞个代换

没有对比就没有伤害,至少直观上面更好用了

对比一下

我们可以直观的给出这样的参数控制
当然啦,这里写的很简单,拉普拉斯变换性质这些没有写,但是我觉得最重要的思想是首先的去领悟。
当然拉普拉斯修改参数值就可以得到傅里叶变换。
不知道你有没有发现,其实上面还是变换的是连续的函数,就是说,有衰减因子,离散版本的拉普拉斯转换还没有着落呢!
Z变换就是有衰减因子,离散版本的拉普拉斯转换。

我最喜欢的书也没有Z变换

安利!
不过令人遗憾的是,Z变换我的领悟并没有很深刻,各位看官可能要失望喽。
这里就是你单看兄弟我一张嘴讲了!
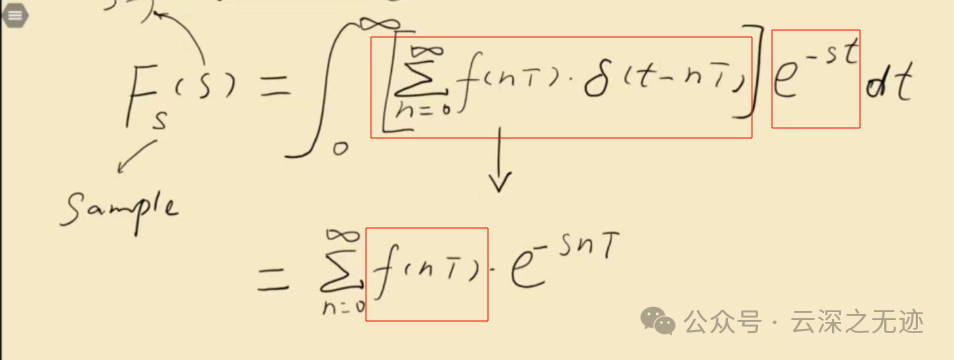
首先上面F里面的S是完整的复数定义,后面就是我们上面打撒的公式,然后乘衰减系数,这里理解没有问题是吧?
然后上面的积分,这里也没有说,这个是卷积积分,离散的话是求和,连续是求积分,是泛函里面的计算,也是广义函数,等我有时间学学。反正就是可以算出来一个值,后面e这个因为就是衰减值,可以直接在积分运算下被保存。
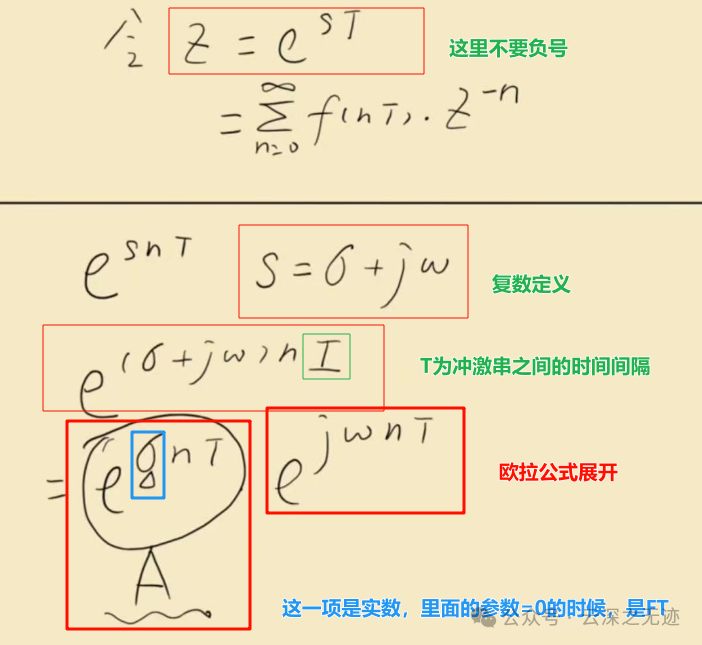
这里单独的讨论最后一项,先不看原来的负号,S就是一个完整的复数,这次展开来计算,T是一个时间项,写完以后,前面的一项A,里面的参数可以控制是不是有衰减。后面这一项使用欧拉公式展开。
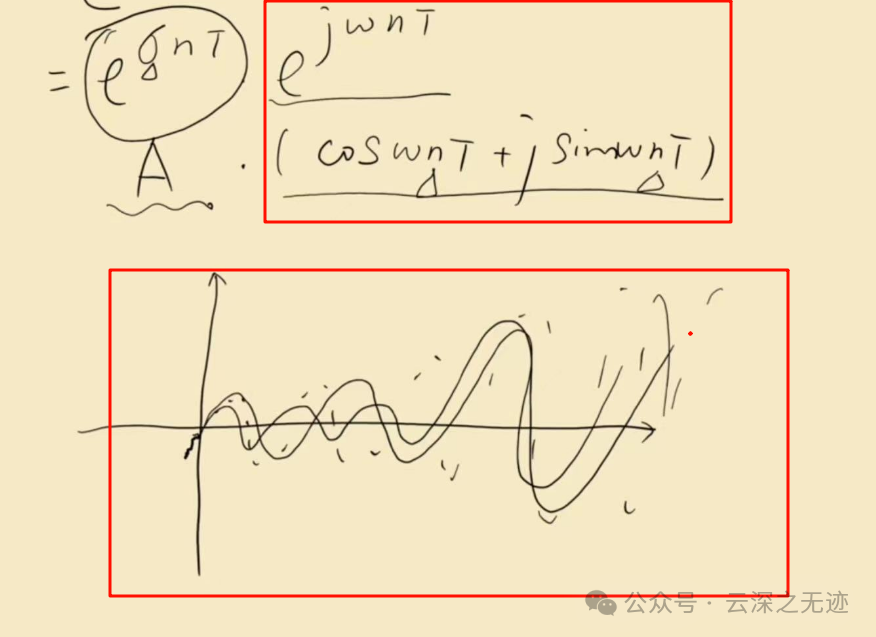
也就是说变成了离散的三角波的点

南大的这个PPT里面写的是很好的

这个就是教科书里面的令Z=e^sT的推导,其实就是把连续离散化,以及n是采样频率的意思。
妈耶,写了这么多,不写了,应该是说明白了,但是很多东西你还得自己看书去算去理解,我缺少了很多证明和性质,只能从直观角度告诉你他们的思想而已,最后这也算我阶段性学习的一个总结。
