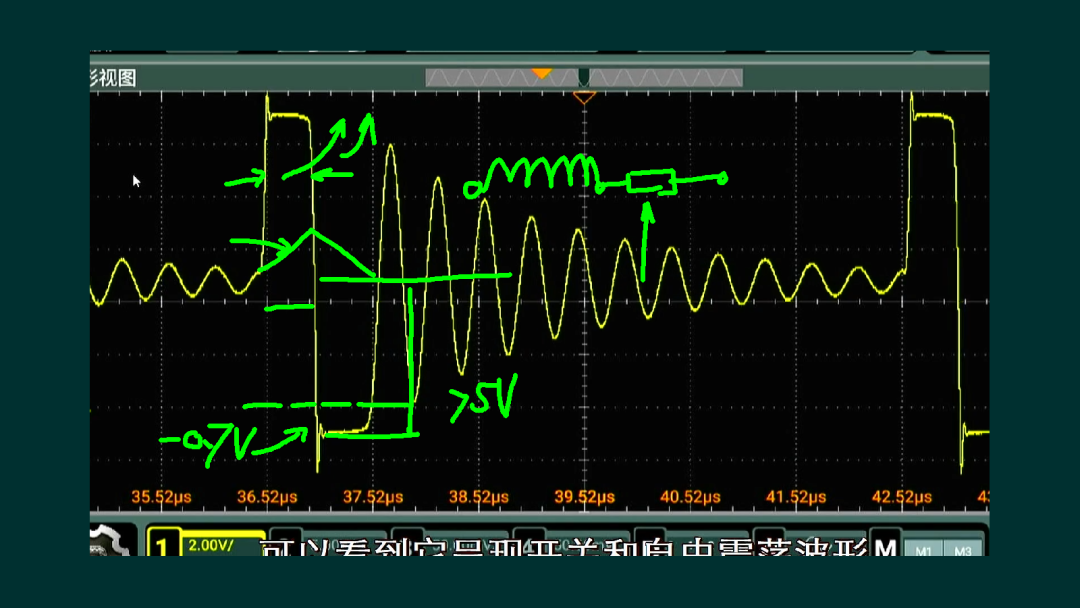
昨天测量了LM2596 开关 电源的震荡波形。在负载轻的情况下,电感中电流是断续的。LM2596导通时间T1 会随着负载电流的增加而上升,下面根据电路图中的参数,通过理论分析,计算一下这个T1的大小,看是是否 与实际测量结果相同。
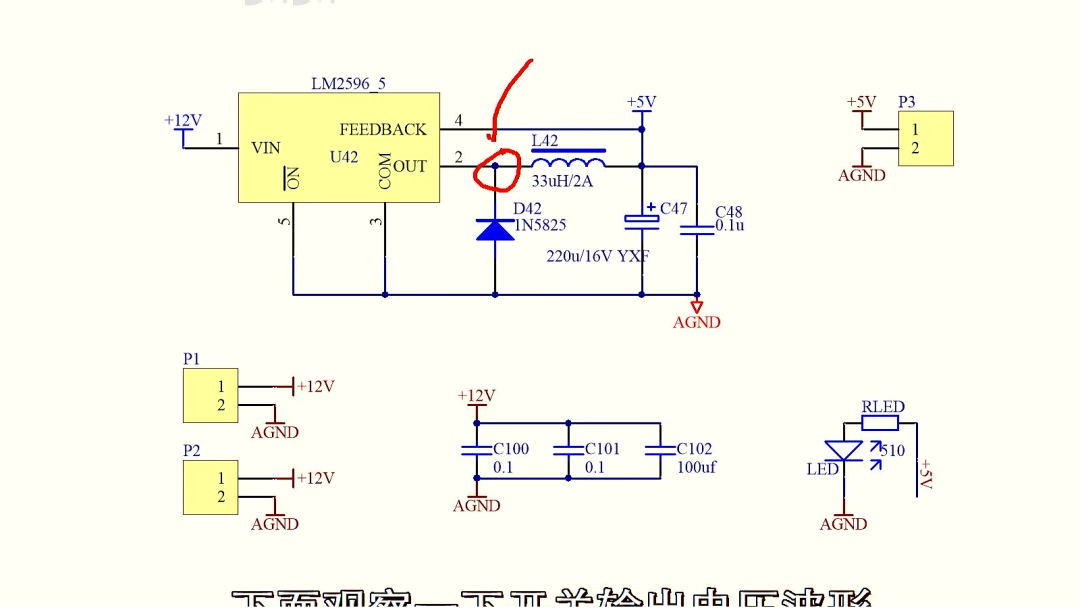
首先,推导一下电流相关的方程。此时,假设LM2596输入电压为 12V,输出稳压5V。在导通期间,电感上的电流增加,在截止期间,二极管续流,电感中的电流降低到 0。此时,导通和截止时间分别为 T1 、 T2。电感正向充电电压为 7V,续流反向电压 5V。电流增加和降低的斜率等于电压除以电感量。根据电流增加和降低幅度相同,由此可以得到 T1、T2 的比值为 5:7。 电流峰值等于上升斜率乘以时间,假设震荡周期为 T,这样,流过电感中的平均电流便可以计算出来,这个电流等于负载电流。 这样,我们变得到了两个方程。
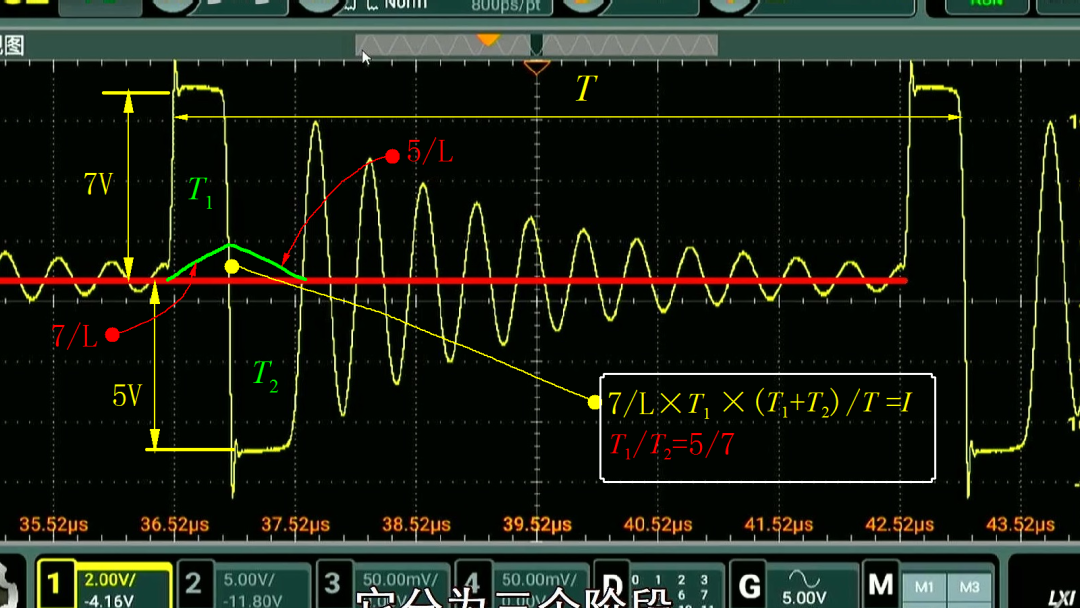
测试电路中,电源的负载只有一个发光二极管,假设LED的电压降为 1.7V,限流电阻已知,这样便可以得到负载电流的表达式。
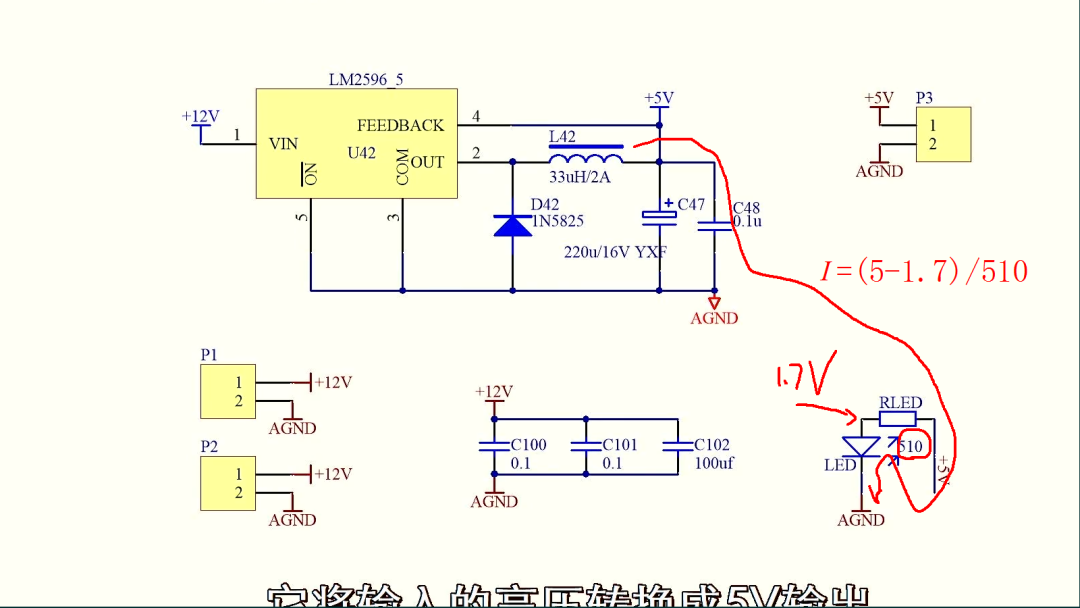
下面将搜得到的公式整理一下,这是分别得到的电源负载电流的方程,再根据T1、T2 之间的比值,以及电路参数。对方程进行合并, 计算,便可以得到 T1 的大小。根据电感,和周期的测量值,可以得到T1的数值,经过计算,得到 T1 等于 0.11 微秒。可是,实际测量T1的时间大约为 4 微秒,经过检查,发现 是平均电流公式计算错误,考虑到是成电流上升和下降,是个三角波形,所以平均电流还要乘以 二分之一。 这样,计算出的T1应该为 0.22微秒。这就与实际测量数值更加接近了。
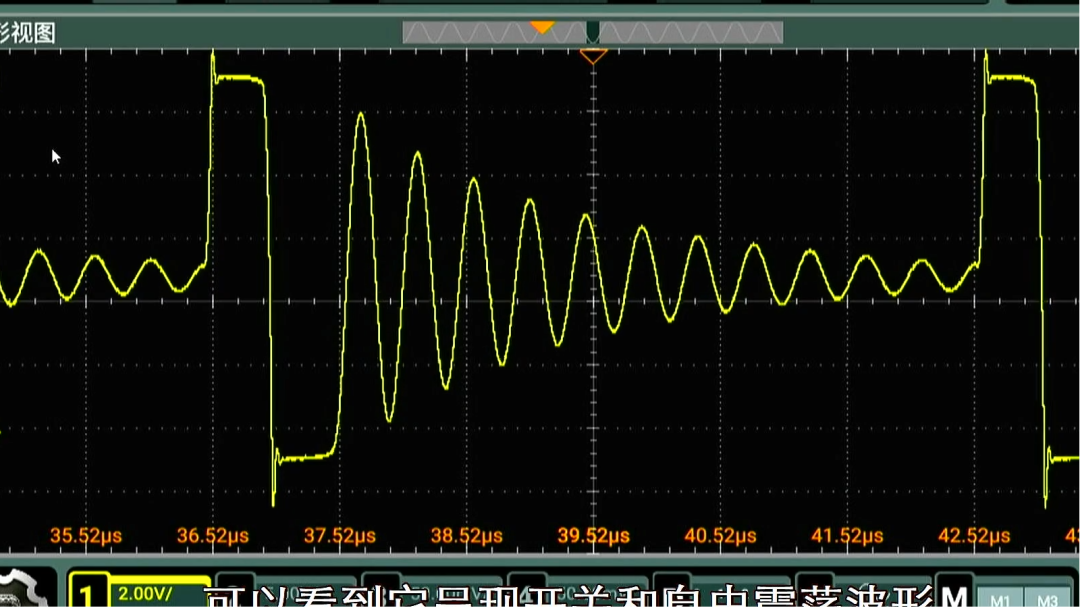
本文对于 LM2596震荡波形中的导通时间 长度进行了推导,计算的数值与实际测量的时间相近。但还是比实际导通时间短。考虑到续流二极管造成续流期间,电感左侧为 0.7V,这就使得电感电流反相电压超过 5V,这会使得正向导通时间增加。此外,实际电感还存在这等效串联电阻,电阻的存在,会使得电流增加速度降低,从而也会增加正向导通时间。考虑到这些原因,便可以进一步修正波形中 导通时间 T1的长度,使其与实际测量数值更加接近。