
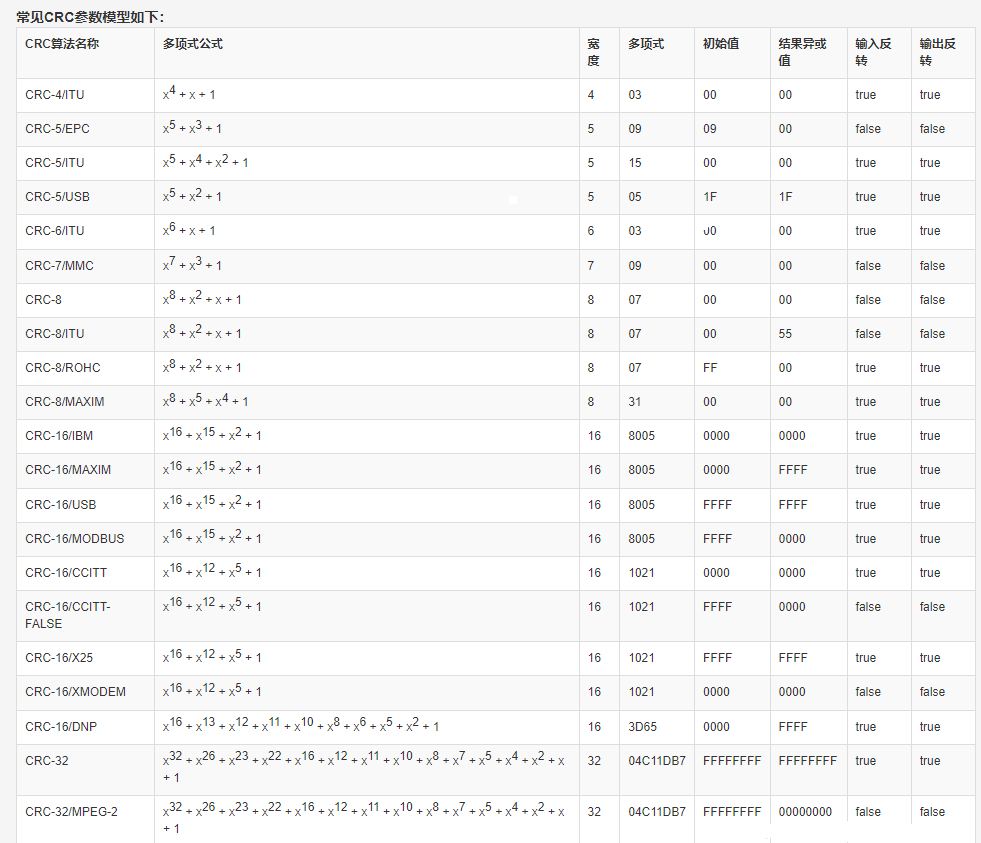
一、CRC简介
循环冗余校验和(Cyclic Redundancy Checksum, CRC)是一种检错技术。
数据通信领域中最常用的一种差错校验码,其信息字段和校验字段长度可以任意指定,但要求通信双方定义的CRC标准一致。主要用来检测或校验数据传输或者保存后可能出现的错误。
在数据传输过程中,无论传输系统的设计再怎么完美,差错总会存在,这种差错可能会导致在链路上传输的一个或者多个帧被破坏(出现比特差错,0变为1,或者1变为0),从而接受方接收到错误的数据。
为尽量提高接受方收到数据的正确率,在接收方接收数据之前需要对数据进行差错检测,当且仅当检测的结果为正确时接收方才真正收下数据。检测的方式有多种,常见的有奇偶校验、因特网校验和循环冗余校验等。
CRC检错能力强,开销小,易于用编码器及检测电路实现,从性能和开销上考虑均优奇偶校验和累加校验。在数据存储和数据通讯领域,多用CRC校验,不能发现的错误在0.005%以下。著名的通讯协议X.25的FCS(帧检错序列)采用的是CRC-CCITT,WinRAR、NERO、ARJ、LHA等压缩工具软件采用的是CRC32,磁盘驱动器的读写采用了CRC16,通用的图像存储格式GIF、TIFF等也都用CRC作为检错手段。
另外,CRC校验多数都是用于检错而不是纠错。
1.1 CRC可检测的错误
• 可检测出所有奇数个错误;
• 可检测出突发长度
• 大部分突发长度=n-k+1的错误可以检测出,其中不可检出的错误占2-(n-k-1);
• 大部分突发长度>n-k+1的错误可以检测出,其中不可检出的错误占2-(n-k)。
其中,n为信息码+监督码总长度,k为信息码长度。
突发错误是指几乎是连续发生的一串错,突发长度就是指从出错的第一位到出错的最后一位的长度(但是,中间并不一定每一位都错)。
1.2 CRC需要知道的基本名称
这里需要知道几个组成部分或者说计算概念:多项式公式、多项式简记式、数据宽度、初始值、结果异或值、输入值反转、输出值反转、参数模型。
1.2.1 多项式公式
对于CRC标准除数,一般使用多项式(或二项式)公式表示,如下图中除数11011(poly值为0x1b)的二项式为G(X)=X4+X3+X+1,X的指数就代表了该bit位上的数据为1(最低位为0)
这里特别注意一下位数问题,除数的位数为二项式最高次幂+1(4+1=5),这个很重要

1.2.2 多项式简记式
通过对CRC的基本了解我们知道,多项式的首尾必定为1,而这个1的位置在下一步计算一定为0,所以就把前面这个1给省略掉了,出现了一个叫简记式的东西,如上例中除数11011的简记式为1011,很多看过CRC高级语言源码的人会知道,对于CRC_16标准下G(X)=X16+X15+X2+1(16#18005)的poly值实际上是8005,这里使用的就是简记式,以后见到的基本都是简记式
1.2.3 数据宽度
数据宽度指的就是CRC校验码的长度(二进制位数),知道了CRC的运算概念和多项式,就可以理解这个概念了,CRC长度始终要比除数位数少1,与简记式长度是一致的。
1.2.4 初始值与结果异或值
在一些标准中,规定了初始值,则数据在进行上述二项式运算之前,需要先将要计算的数据与初始值的最低字节进行异或,然后再与多项式进行计算。
而在结果异或值不为零的情况下,则需要将计算得到的CRC结果值再与结果异或值进行一次异或计算,得到的最终值才是我们需要的CRC校验码。
这里可以看出,初始值与结果值的位数要求与数据宽度一致。
1.2.5 输入值反转与输出值反转
输入值反转的意思是在计算之前先将输入数据反转,然后再计算。如对于输入数据,其正向值为1 1000 0000 0000 0101,反转值则为1010 0000 0000 0001 1,注意这里反转并不是按位取反,而是低bit位与高bit位交换位置
输出值反转则是将最终得到的CRC结果反转。
通常,输入值反转后的结果值也会是反转的,所以这两个选项一般是同向的。
二、CRC校验原理
CRC校验根本思想就是先在要发送的数据帧后面附加一个数(这个就是用来校验的校验码),生成一个新帧发送给接收端。当然,这个附加的数不是随意的,它是数据帧除以选定的CRC除数产生的余数
新帧到达接收端后,有两种方法比较传输是否出错:
一是用同样的方法对数据帧除以CRC除数产生的余数跟校验码相比,如果相同,则数据正确,否则数据错误;
二是对新帧除以CRC除数,如果余数为0,则数据正确,否则数据错误。
要校验的数据加上此数据计算出来的crc校验码组成新的数据帧,如下图所示。

2.1 CRC校验计数基础知识
CRC校验中的运算不是普通的运算,称为“模2运算”
模2加法和减法都是异或运算,例子如下:
1010+0110=1100,1010-0110=1100
模2乘法的定义:
0×0=0,0×1=0,1×0=0,1×1=1。1011×101=100111

其中横线之间的累加过程,采用的是2进制加法,不进位。
模2除法,其实也是异或运算:
0/1=0,1/1=1。1011/101=10,余数为100(补了2个0)。

2.2 CRC多项式的选择(除数的选择)
对于CRC标准除数,一般使用多项式(或二项式)公式表示(参照节1.2.1和1.2.2),CRC除数位数越高,检错能力越强,通常是根据设计中的数据流大小与格式来选择。数据流是8bit为一个包的话,则CRC校验位数选择8bit或者16bit等比较好。
三、CRC校验码手动计算
CRC校验码就是两个数相除的余数,而且余数位数要正好比除数少一位,即使MSB为0。
下面举例说明CRC校验码手动计算过程:
对于数据1110 0101,指定多项式为x4+x3+x+1,则除数为11011。首先要将数据左移4bit(校验码的位数),然后再进行计算:

将上面计算得到的校验位补到数据的后面就构成了要发送的新数据帧:

四、CRC校验算法推导与Verilog实现
第三大节讲了如何手动计算CRC校验码,但如何在编程中实现,这就是个难题,网上很多文章都只是浅浅地谈了一下,并没有具体推导,如果对推导过程没兴趣的,可以直接翻到第五大节直接用链接生成Verilog代码。
4.1 生成矩阵G
CRC是循环码的一种,这是通信原理上的内容。由生成矩阵G,就可以由k个信息位得到整个码组,即要传输的完整数据(信息码+监督码):
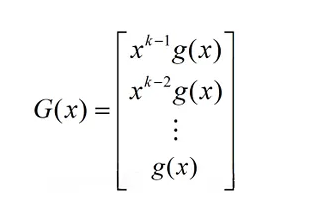
其中,g(x)是唯一的(n-k)次生成多项式,xk与g(x)相乘是使其左移k位。G(x)为生成矩阵,与4.2中G(x)意义不同(我懒得改了)。整个码组A(x)为
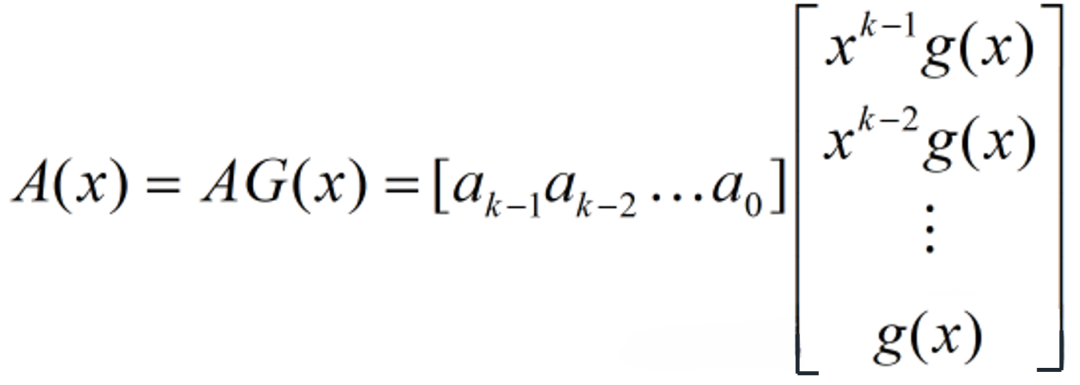
其中,A为输入数据矩阵。以CRC4举例,多项式为x4+x+1(10011),输入数据为5bit举例
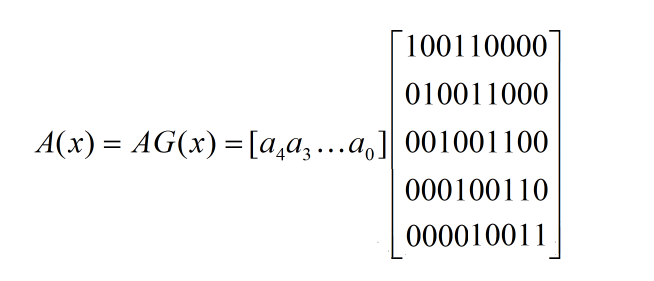
输入数据矩阵A,就可以得到相应的数据码,计算结果中前5bit为信息码,后4bit为监督码
4.2 CRC校验公式
CRC校验码其实是两个多项式相除的余数,我们要传输的数据(也是被除数)是多项式M(x) 的系数,除数是生成多项式G(x) 的系数,G(x) 的最高次幂为xn-k ,校验码是余数多项式R(x) 的系数,Q(x) 为商,则计算公式为
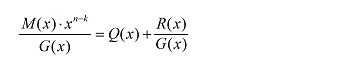
4.3 CRC串行计算公式推导
上面的式子其实已经可以计算得到CRC校验码了,但还无法在硬件上实现,所以需要用硬件的思想推导可实现的计算方法,这里以CRC-32的标准来进行举例推导。
根据二进制信息码转换成多项式的方法,对于任意一个长度为(m+1)的二进制信息码,可以转换成一个最高次幂为m的多项式:
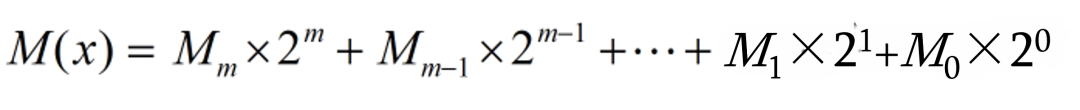
其中,2m 是二进制的科学计数法。
为求此二进制序列的CRC值,首先将M(x) 乘以232,然后再除以生成多项式G(x),所得余数R(x) 是一个最高次幂为31的多项式,其系数为CRC-32的值,那么:
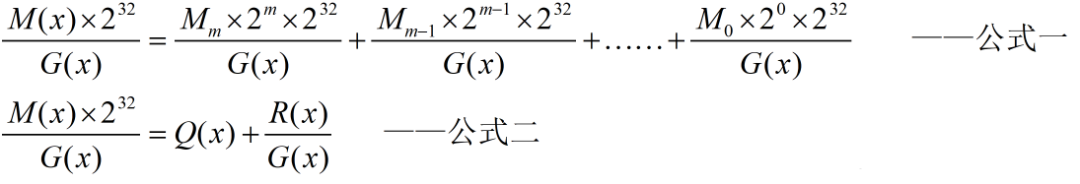
先从最高位开始解,
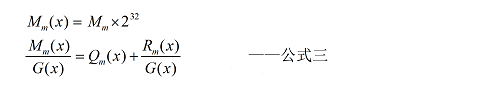
结合公式一、公式二与公式三可得:
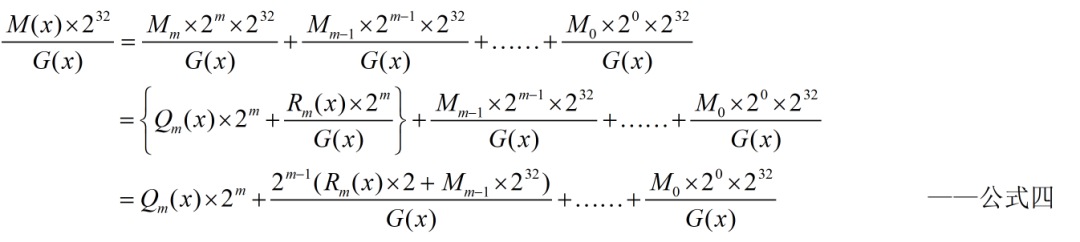
接着解次高位,在公式四中,最高位的余数与M(x)次高位的和除以G(x),可得到次高位的商和余数:
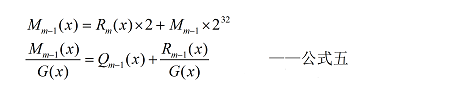
将公式五代入公式四中:
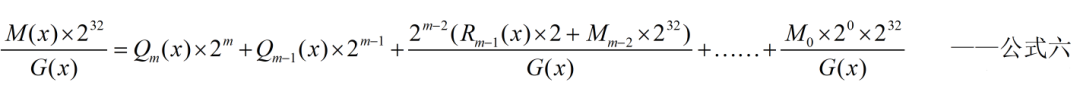
以次类推可得最终公式:
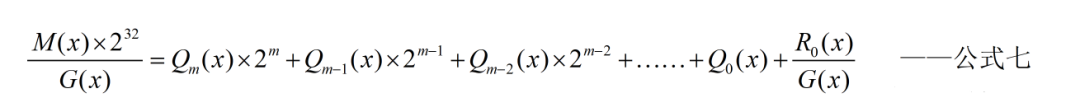
以上推导过程的前提是串行计算,即先计算多项式M(x)最高位以G(x),得到最高位的商和余数;最高位的余数与M(x)次高位求和除以G(x)得到次高位的商和余数……如此反复计算直到运算完最低位得到的余数R0(x)对应的系数即为我们的CRC-32的校验码。
以上推导过程表明:一个m+1位的二进制序列,可以按位求取CRC-32的值。运算时,首先从最高位(第m+1位,设最右边的为第1位)开始计算,然后依次计算较低位。因此,每一位的CRC-32运算就转化成了一个最高次幂为32的多项式除以一个最高次幂为32的多项式(生成多项式),结果(余数)为一个最高次幂不超过31的多项式。
4.4 CRC校验串行计算的Verilog实现
4.1和4.2节讲了公式推导,这一节讲如何用Verilog表达出来。
首先得了解LFSR,线性反馈移位寄存器简称LFSR,用于产生可重复的伪随机序列,也可用来实现CRC校验。LFSR主要由触发器(寄存器)、异或门以及反馈线路组成。
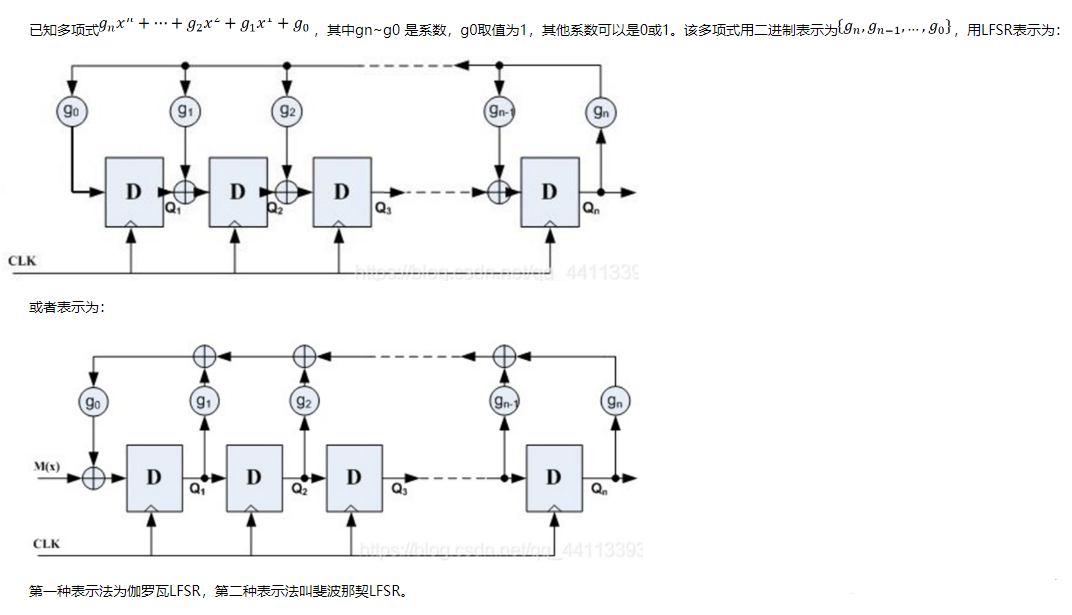
通常推荐伽罗瓦LFSR,如图所示,对于二进制来说,gn 到g0的各个系数表示这条支路是否存在,1为存在,0则不存在。各个寄存器储存着上一次CRC校验运算的结果,寄存器的输出即为CRC的值,这里还是以CRC-32举例,其生成多项式为:
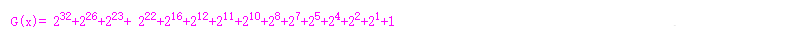
当输入新的位参与运算时,信息多项式为:

上一次CRC计算的结果为:
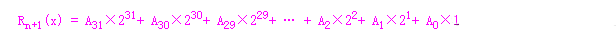
根据上一节推导出的公式,新的CRC-32值Rn(x) 为 {Rn+1(x)×2 + M(x)}/ G(x) 的余数。设
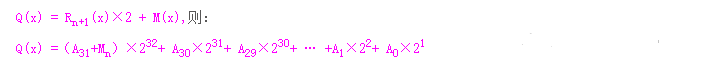
在计算Q(x)/G(x) 的结果时,根据模2运算法则,如果A31+ Mn 的结果为1,则商为1,余数为Q(x)-G(x) ;如果A31+ Mn 的结果为0,则商为0,余数为Q(x) 本身。其中,A31+ Mn 是模2加法;Q(x)-G(x) 是模2减法。
当上一个CRC-32结果的最高位A31和输入的数值Mn模2加法结果为1时,上一次CRC结果右移一位,完成乘2的过程,再与G(x)多项式的系数进行异或运算,完成减法。由于任何数与0异或保持不变,所以LFSR中只有在G(x)多项式为1的系数处才放置异或门。运算完毕以后把结果存入寄存器即为新的CRC-32值。
当上一个CRC-32结果的最高位A31和输入的数值Mn模2加法结果为0时,Q(x)不够除,Q(x)本身作为余数存入寄存器,获得新的CRC-32值。由于A31+ Mn的结果为0,异或门不起作用,Q(x) = A30×231+ A29×230+ … +A1×22+ A0×21,由Rn+1(x)右移一位获得, Q(x)的0次幂为0,刚好把A31+ Mn的结果作为输入。
4.5 CRC校验并行计算的Verilog实现
4.3节是串行的表述,每一bit数据需要一个时钟周期,为提高速率还得用上并行计算的思想,输入数据S要并行输入到G(x)系数为1的支路中,输入数据从输入端按高到低逐bit输入,就可以实现。
假如被除数是2位的数据S[1:0]=01,多项式是10011,x4 +x+1。在CRC校验里面,习惯省略最高位的1,多项式用0011表示。那么S除以0011的模二运算数字电路结构为:

其中d1~ d4是寄存器输入;q1~q4是寄存器输出。寄存器需要赋初值,一般赋全1或全0。
d1=S[1]^q4;
d2= S[1]^ q1^q4;
d3=q2;
d4=q3。
经过一次移位后:
q1=d1= S[1]^q4;
q2= d2= S[1]^ q1^q4;
q3= d3=q2;
q4= d4=q3。
此时有:
d1=S[0]^q3;
d2= S[0]^ S[1]^ q4^q3;
d3= S[1]^ q1^q4;
d4= q2。
令c[3:0]={q4,q3,q2,q1},d[3:0]={d4,d3,d2,d1},那么d就是最终的运算结果表达式,如下
d[3]=c[1];
d[2]= S[1]^ c[0]^c[3];
d[1]= S[0]^ S[1]^ c[3]^ c[2];
d[0]= S[0]^ c[2]。
令c的初值为0,则01对0011的模二除法的余数为0011。
再比如多项式为x5 +x3 +x+1,简记式为01011,其数字电路结构为:
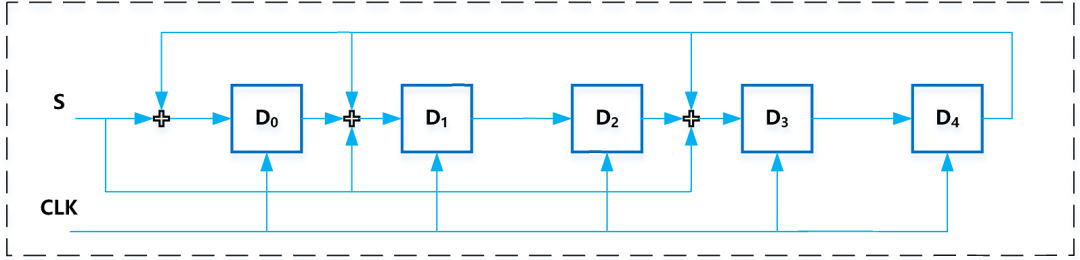
输入数据S要全部输入完,寄存器得到的结果才是最后的结果。同理可推导出其他多项式和输入数据的情况。
4.6 CRC校验在多个字节(数据包)场景下的计算方法
对于多个字节(数据包),这里举个例子,如果数据是10bit*100个包,则每次输入10bit得到校验码后,该检验码为下次数据计算时寄存器D的初值,如此反复计算得到最后的检验码添加到整个数据后面即可,而不需要每个数据包后面都添加检验码。
文章来源:https://blog.csdn.net/qq_42446721/article/details/127054205
版权归原作者所有