
信号与系统2024(春季)作业要求以及参考答案汇总[1]
信号与系统2024(春季)作业要求 - 第十二次作业[2]
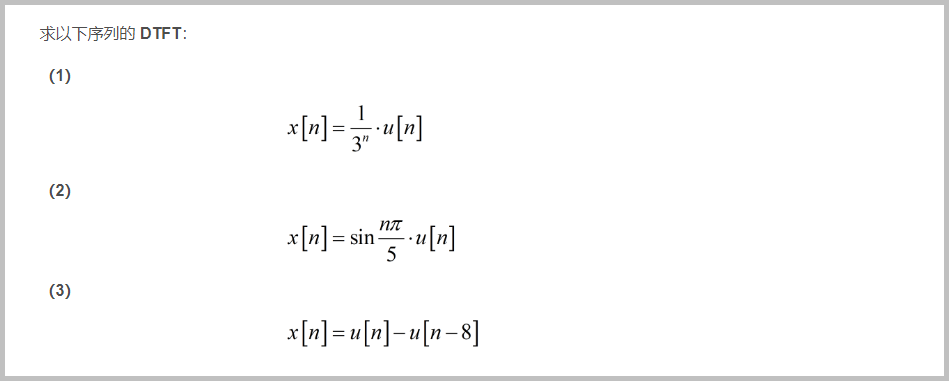
□ 解答:
(1)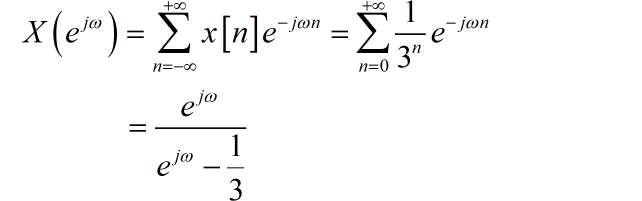
(2)
序列的 z 变换为:
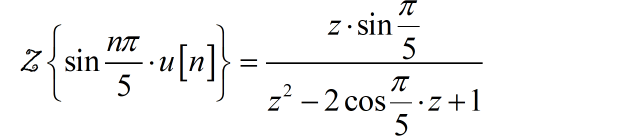
那么对应序列的傅里叶变换为:
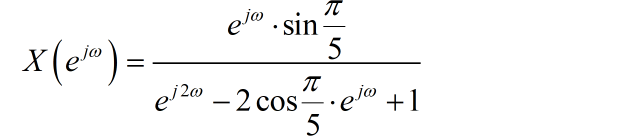
(3)
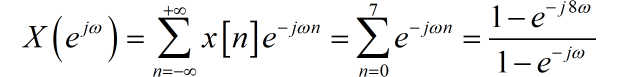
□ 解答:
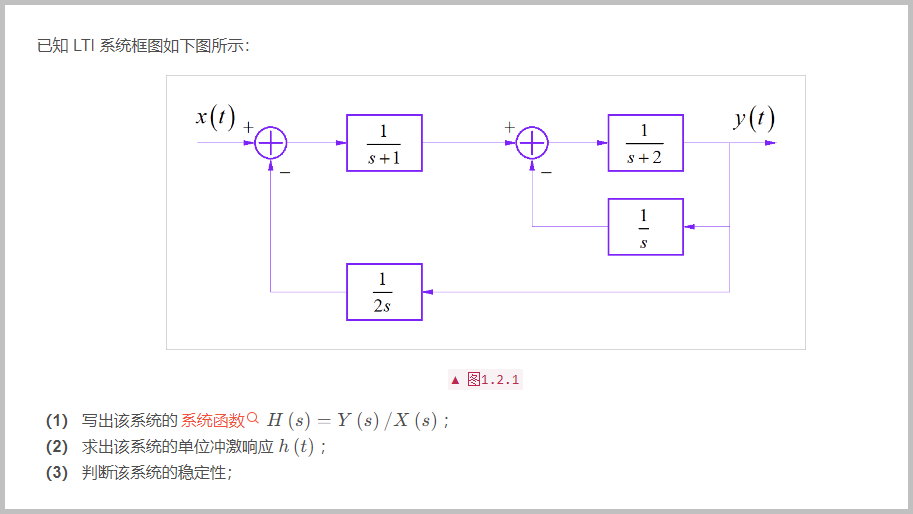
(1)
在原来作业给定的系统框图中,最下面的反馈系数是 。这对系统化简到来了麻烦。下面将它修改为 。这样后面系统求解就比较简单了。下面的求解过程,是按照修改后的系数进行求解的。
设置输入输出信号的 Laplace 变换分别为 。根据系统框图,可以写出各个节点对应的表达式。根据最后一个综合器的输出和输入之间的关系,可以写出对应的方程为:
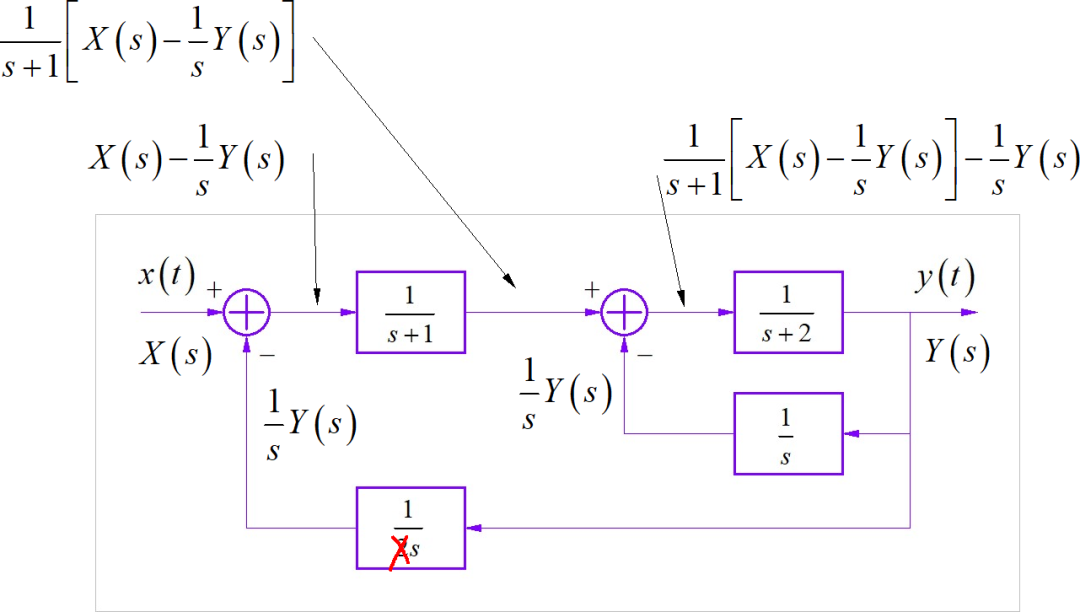
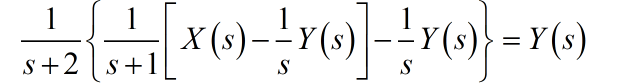
化简上面公式,可以获得系统方程为:
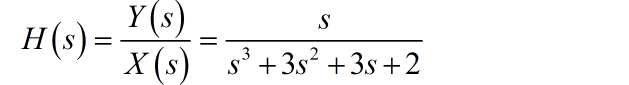
(2) 将 进行因式分解:
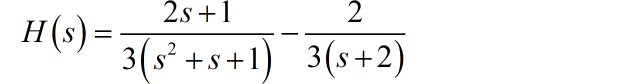
根据常见信号的 Laplace 变换表格,可以给出上面两个二次分式和一次分式分别对应的信号,系统的单位冲击响应为: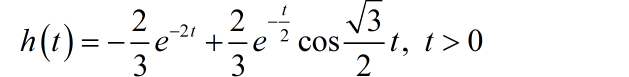
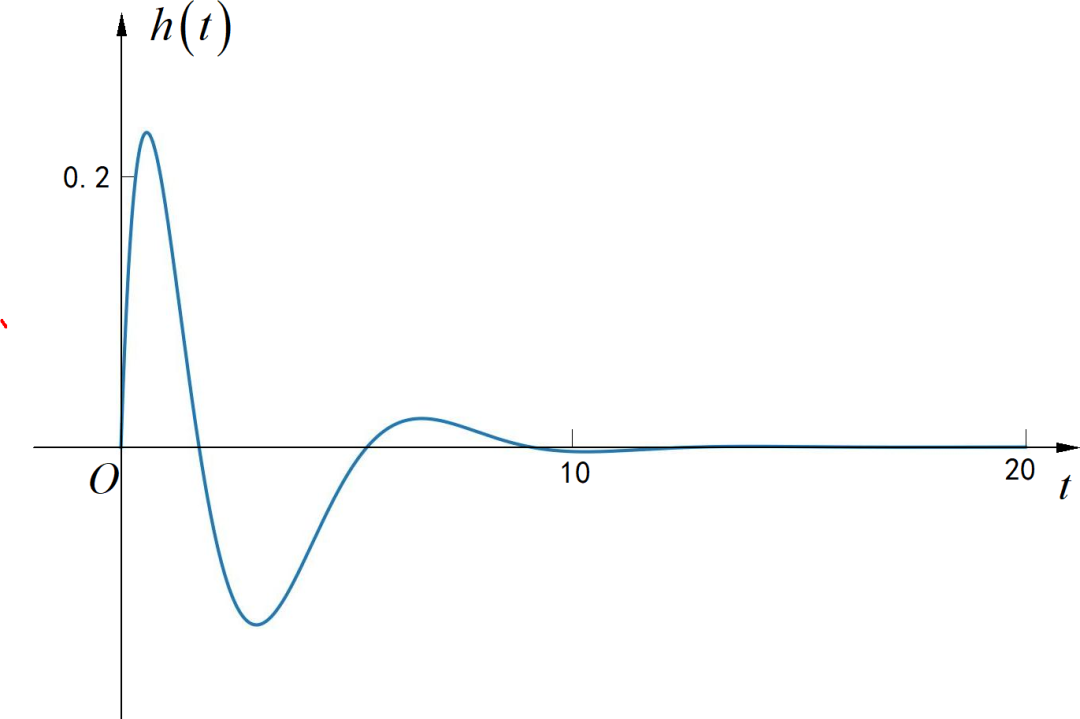
(3) 因为 是指数衰减,满足绝对可积,系统是稳定的。
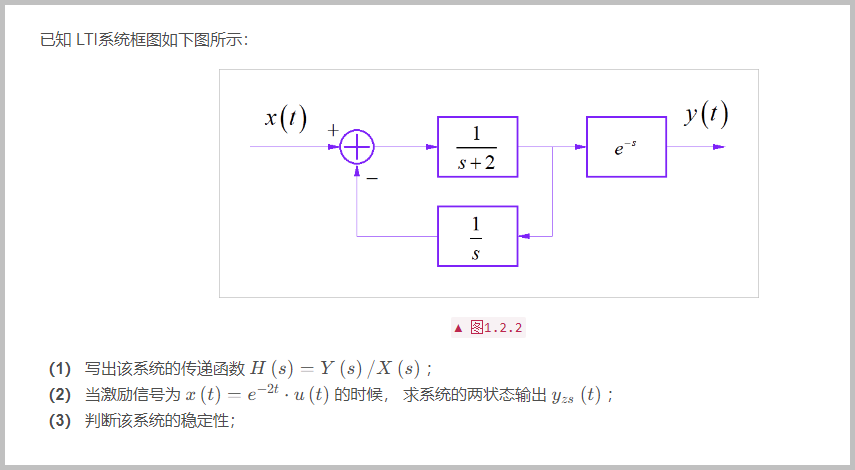
□ 解答:
(1) 先不考虑最后一个延迟环节。首先根据综合器写出输入输出之间的方程。

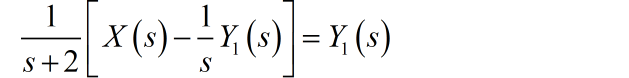
化简这个方程,可以得到:
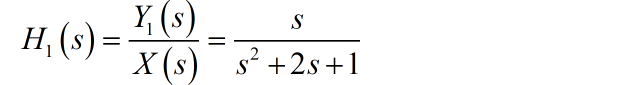
再增加上最后的延迟环节,可以得到:
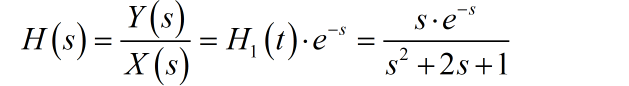
(2)
输入信号的 Laplace 变换为:

系统的零状态输出为:
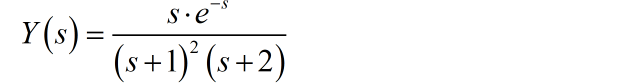
对 进行因式分解:
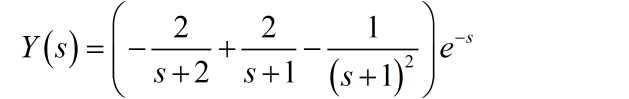
对应的时域信号为:

(3) 该系统是稳定系统 。
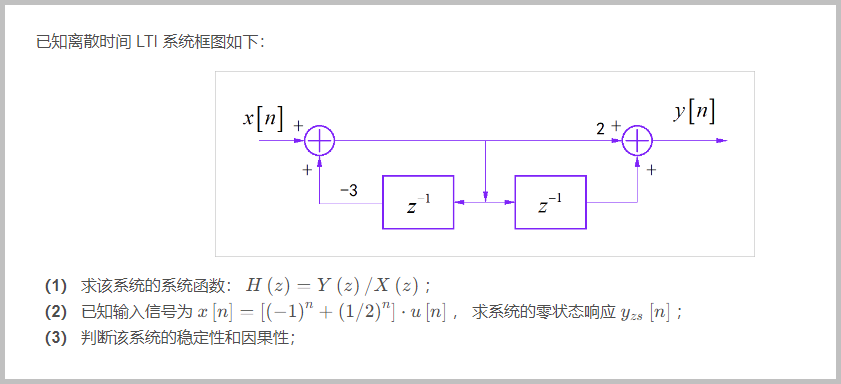
□ 解答:
(1) 在系统框图中间增加一个中间变量:
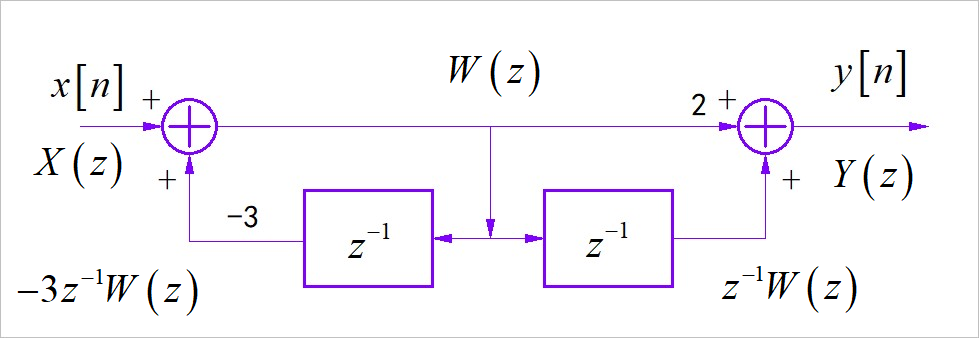
根据前后两个加法器,得到两个方程:
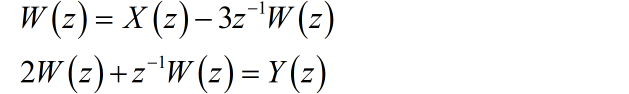
消去 ,得到系统函数:
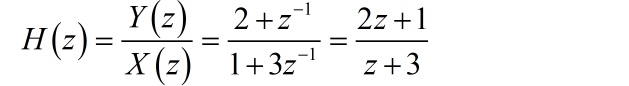
(2)
输入信号的 z 变换:
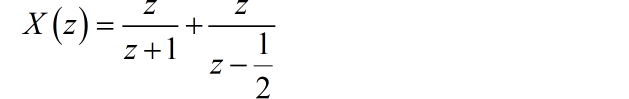
系统的零状态输出为:
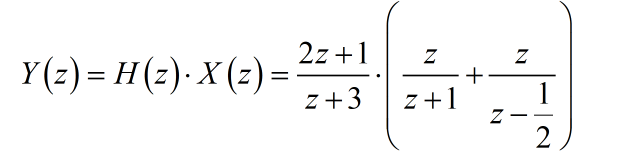
进行化简:
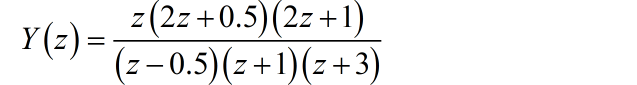
进行因式分解: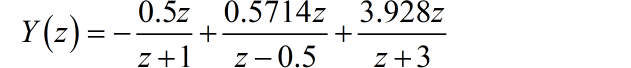
对应的时域序列为:
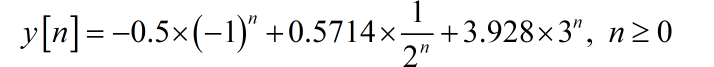
(3) 该系统为不稳定系统。这是因为,该系统的系统函数中包含有单位圆之外的极点,以及一个在 (-1)处的极点。

□ 解答:
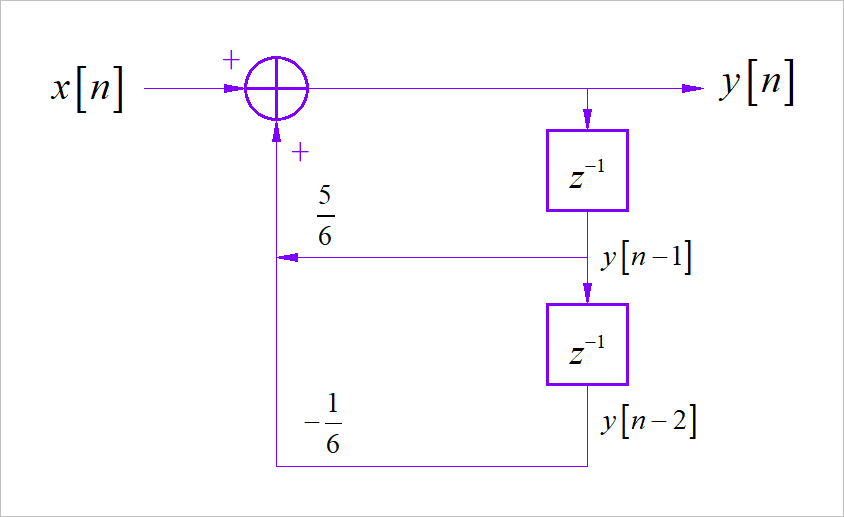
(1) 根据系统的零极点的分布,可以写出系统函数: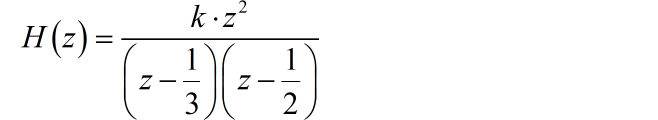
其中 是待定系数。根据系统的初值 ,由 z 变换的初值定理:
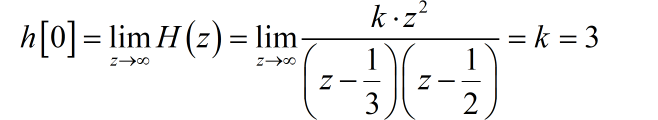
因此,系统函数为:
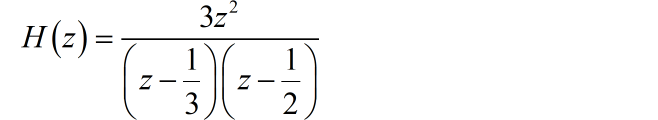
系统的单位样值响应 是系统函数 的 z 反变换结果。将 进行因式分解:
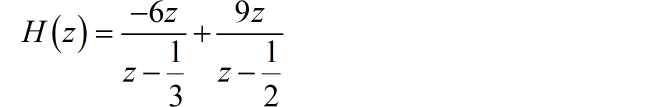
那么,对应的右边序列为: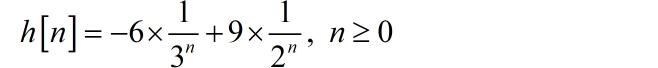
(2) 系统的单位阶跃响应为:

利用因式分解方法,求 。
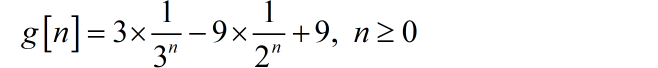
(3) 根据系统函数,绘制出一个对应的系统框图: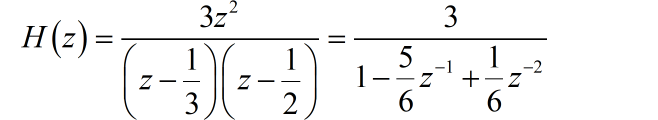
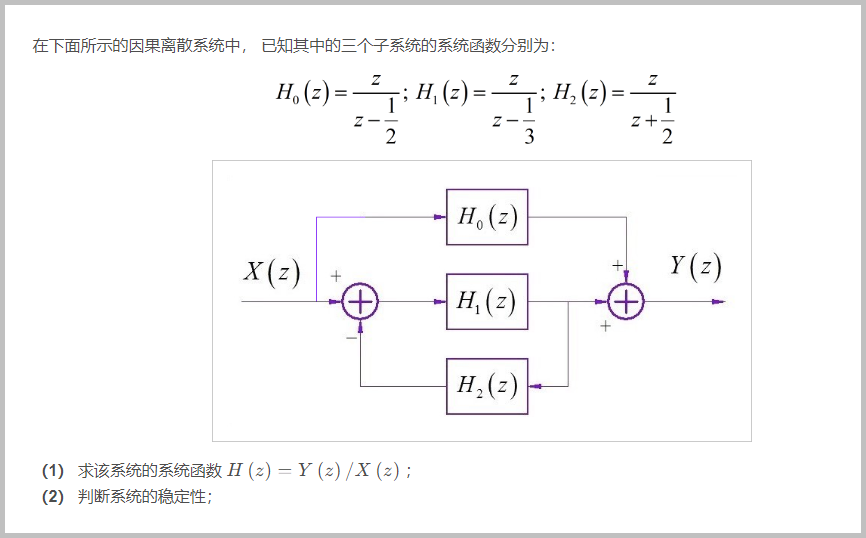
□ 解答:
在系统框图中添加中间临时变量 。写出系统中各分支对应的变量。
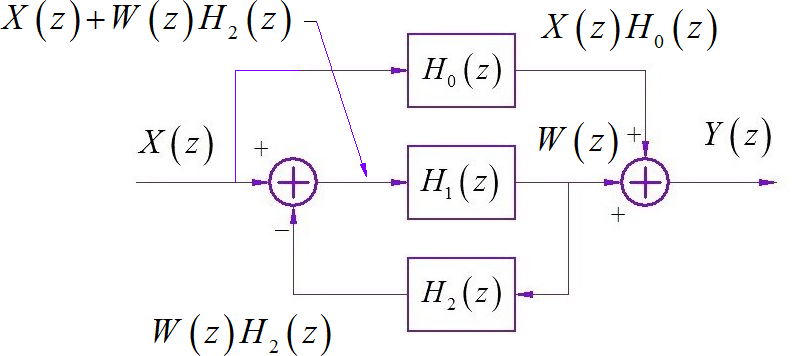
▲ 图1.1.4 设置了中间变量的系统框图根据系统框图中累加器关系,可以得到如下方程:
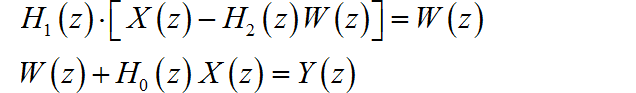
消去 临时变量,得到系统函数:
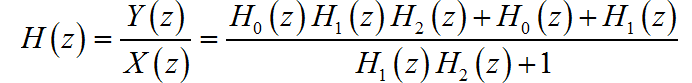
根据系统给出的 表达式,代入上面 ,可得:
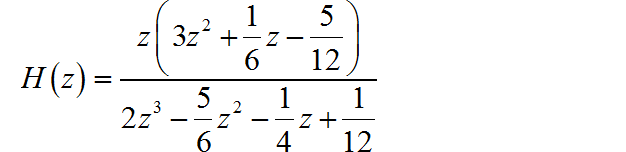
进行因式分解,可得: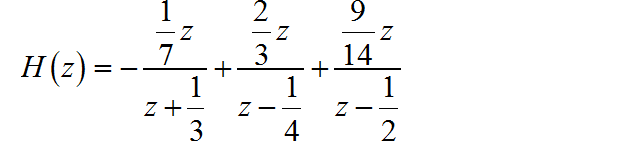
写出相同响应对应的右边序列:
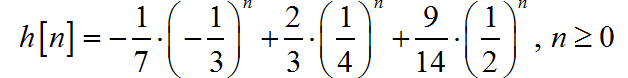
(2) H(z) 的极点都在单位圆内,系统是稳定的。

□ 解答:
根据系统函数的定义 ,由题目中给定的输入输出信号的变化,可以求出系统函数:
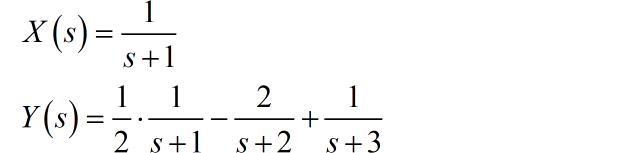
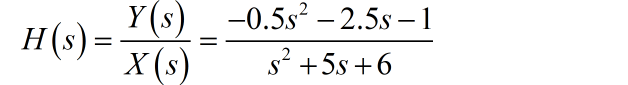
系统的单位冲激响应 是系统函数 的Laplace变换。将 进行因式分解,这样便于写出 的表达式。
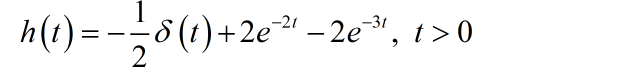

□ 解答:
根据系统函数的定义, ,所以系统的输入为: 。根据已知的 ,求出它们对应的 Laplace变换:
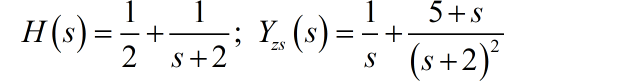
那么,
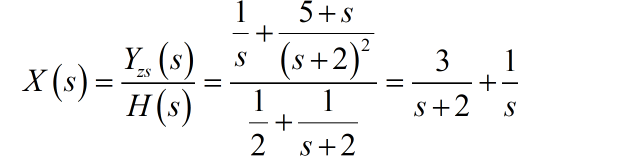
因此,可以知道输入信号 为:


□ 解答:
根据系统的差分方程,可以写出系统的系统函数:
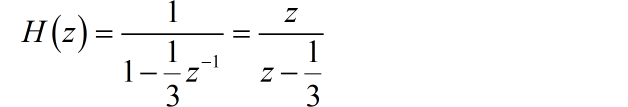
根据系统的零状态输出,写出对应的 z 变换:
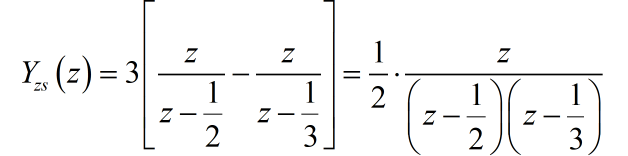
所以系统的激励信号 的 z 变换为:
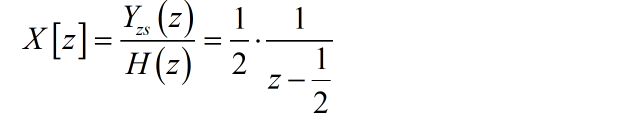
对应的时域序列信号为:

□ 解答:
(1) 这个题目原来是在第二章,现在在 Laplace 变换域内讨论这个题目的求解过程。将两次系统的输入和输出都进行 Laplace 变换。
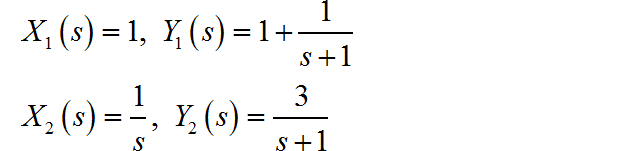
系统的完全输出等于零状态响应加上零输入响应:
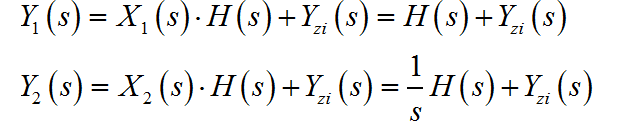
上面两个表达式相减,可得:
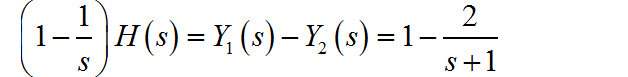 所以
所以

进行 Laplace 反变换可得:
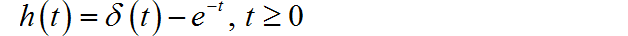
(2) 根据已经求得的 ,可以求得 :
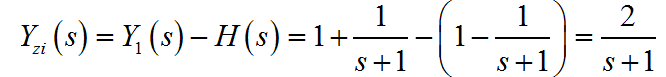
进行 Laplace 反变换,可得:

(3)
将 进行 Laplace 变换:
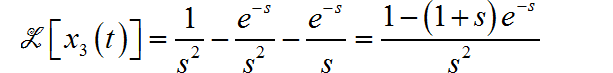
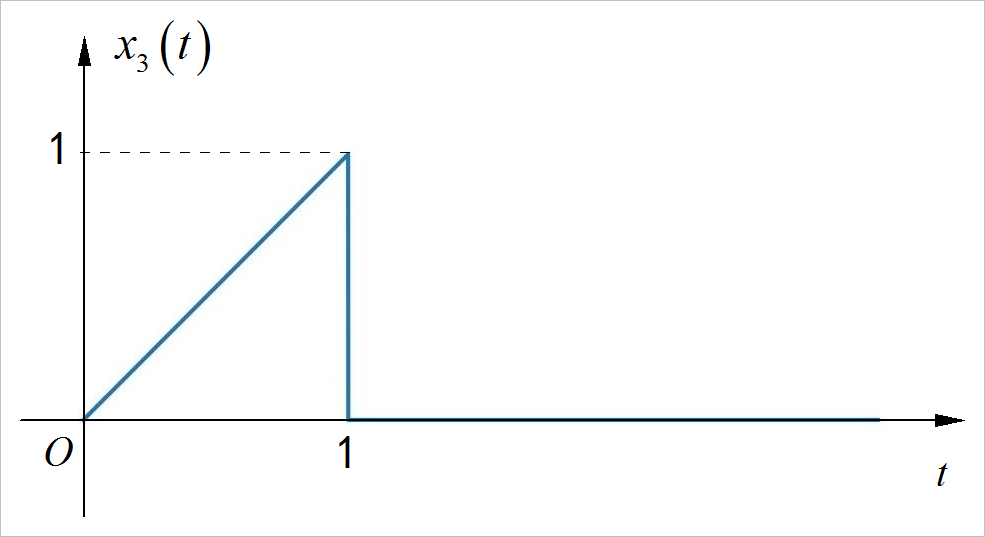
▲ 图1.2.2 x3(t)信号那么系统的完全响应为:
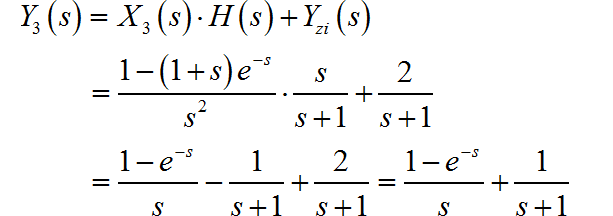
对应的时域信号为:
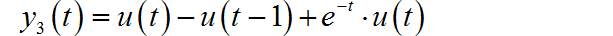
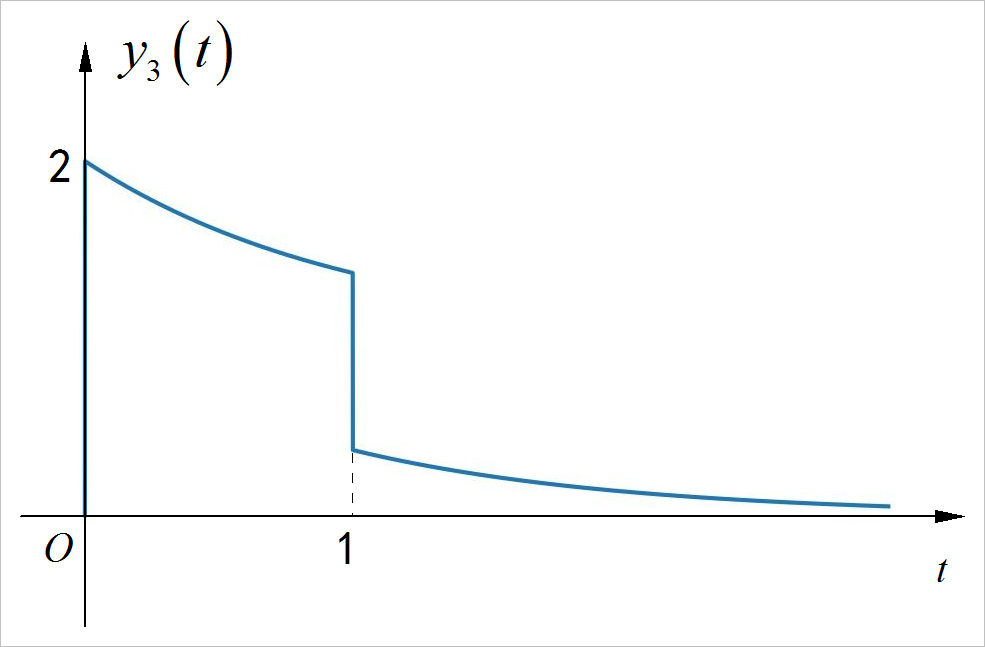
▲ 图1.2.3 系统的完全响应 y3(t)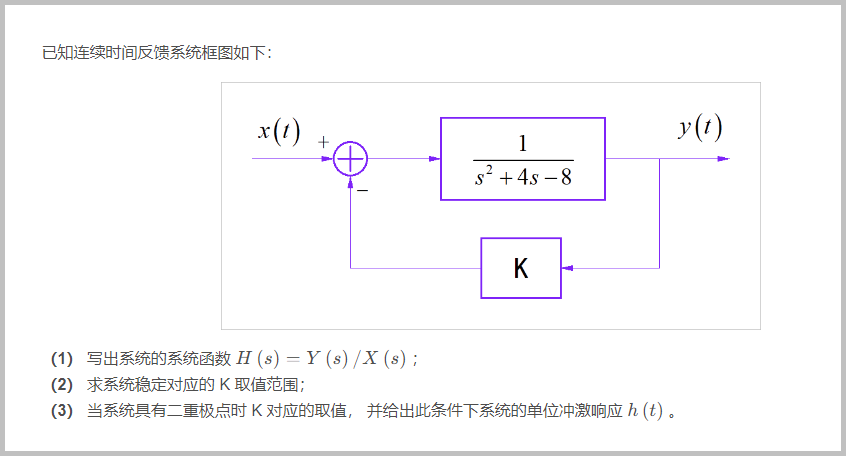
□ 解答:
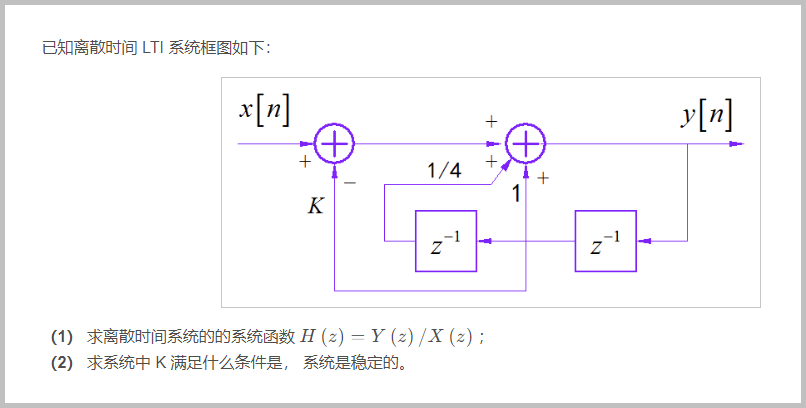
(1) 根据系统框图,可以写出系统函数:
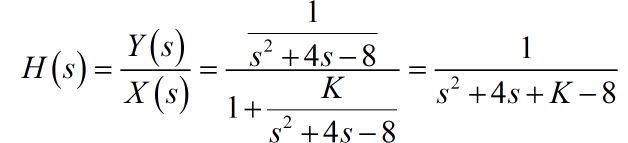
(2) 系统的两个极点分别为:
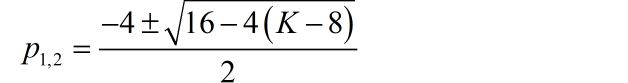
当 的时候,对应的极点都位于 s 平面的左半平面,系统稳定。
根据 Routh 定理,对于 2 阶多项式,当所有的系数正负符号都相同(本题都是大于0),对应的根都位于左半平面。由此,也可以得出相同的结论。
(3) 当 ,即 。系统函数具有二重极点。基点为: 。此时,系统函数为:

对应的系统函数为:

□ 解答:
(1) 根据系统框图,可以得到如下方程:
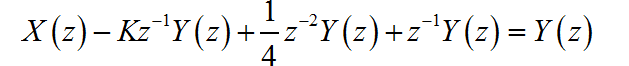
简化之后,可以得到系统的系统函数为:
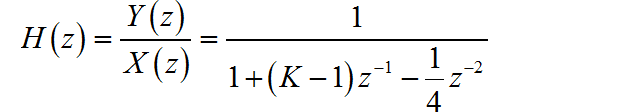
(2) 整理系统函数如下:
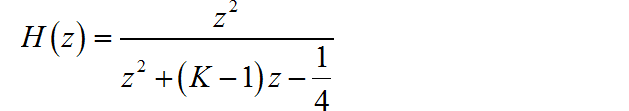
系统函数的两个极点分别为:
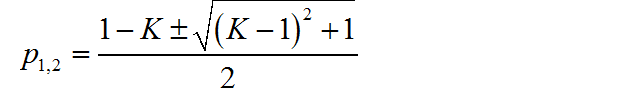
下面绘制出l个极点对应不同 K值变化情况。
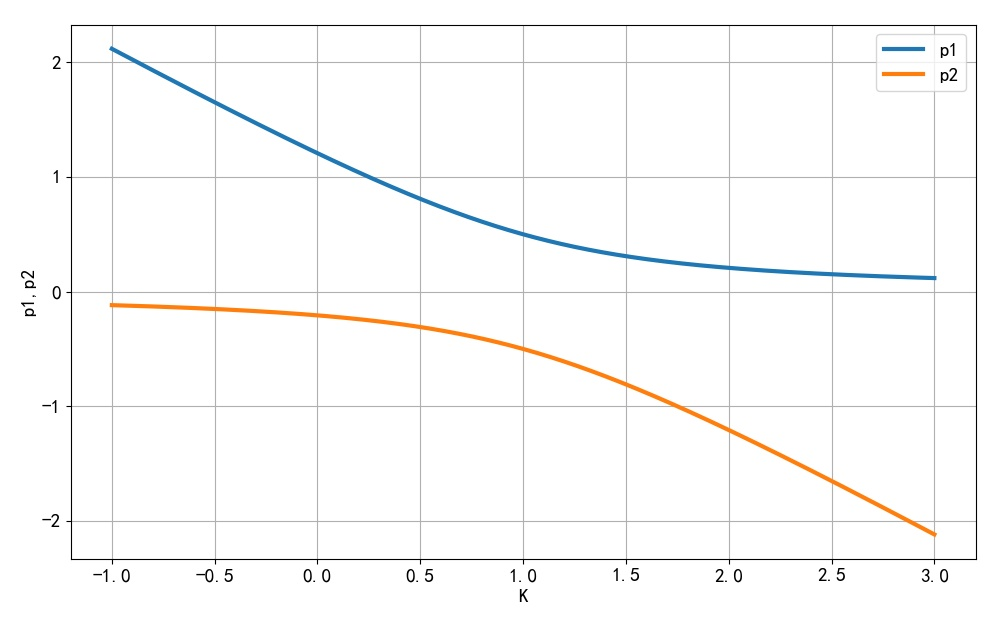
▲ 图1.3.1 不同的K对应两个极点的取值分别求出一下两个方程对应的根,可以知道 K 取值在 之内时,两个极点都位于单位圆内。
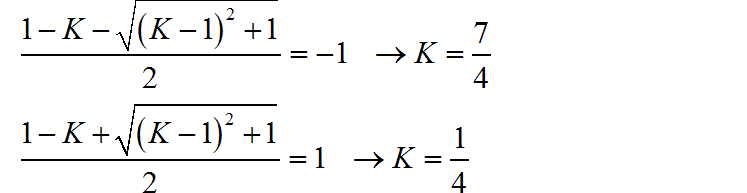
因此,当 时,系统是稳定的。

□ 解答:
(1) 根据差分方程,得到系统的系统函数为:
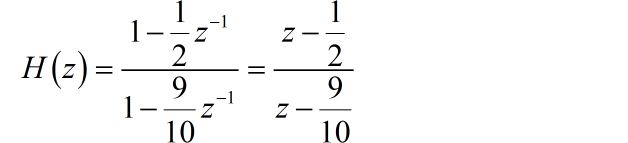
根据题意,该差分方程对应的是一个因果 LTI 系统。系统函数中的极点 位于单位圆之内,所以该系统为 “稳定系统”。
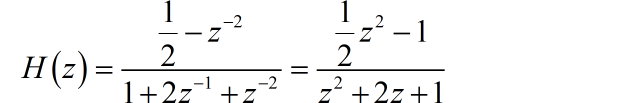
根据题意,该差分方程对应的是一个因果 LTI 系统。它的系统函数具有一个二阶极点: 。位于单位圆上,所以该系统是一个 “不稳定系统”。

□ 解答:
(1) 因果系统
(2) 非因果系统
(3) 非因果系统
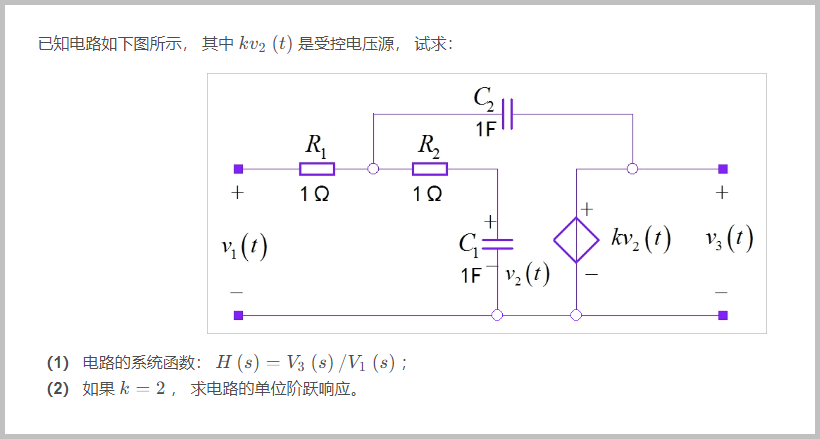
□ 解答:
(1) 为了 ,分别考虑在 和 作用下,在 上所形成的电压。
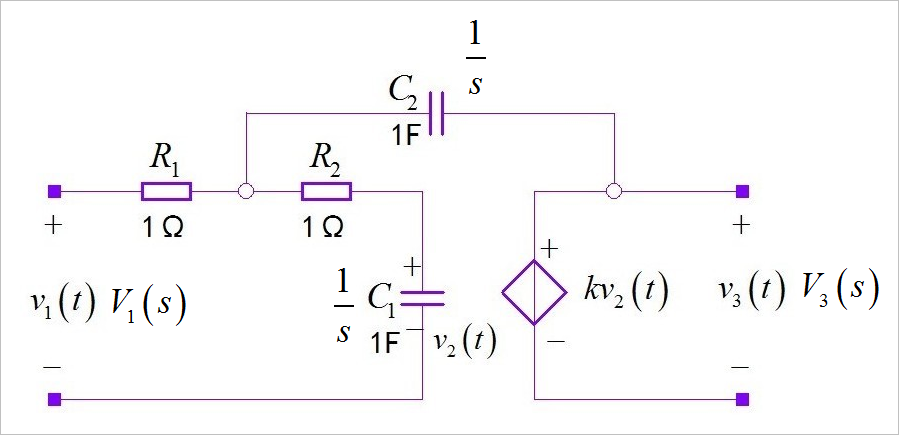
▲ 图1.5.1 s域内的电路图考虑 时,仅仅在 作用下 C1 上的电压:
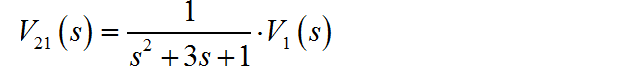
考虑 时,仅在 作用下,C1 上的电压:
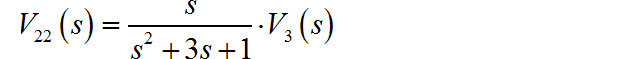
所以:
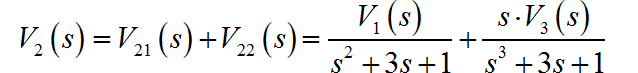 在根据
在根据
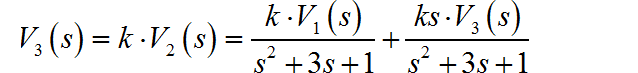
对上面表达式进行化简:
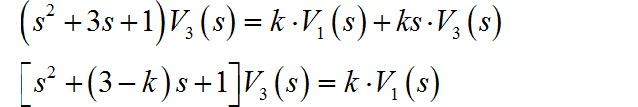
电路的系统函数为:
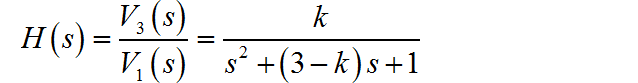
(2) 当 时,对应的电路系统函数为:

进行 Laplace 反变换,可以得到电路的单位冲击响应:
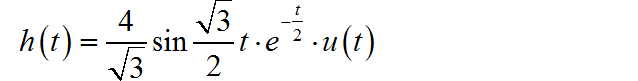
电路的单位阶跃响应:
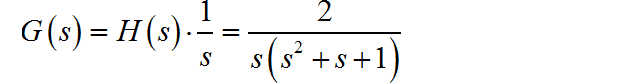
进行 Laplace 反变换,可以得到电路的单位阶跃响应:
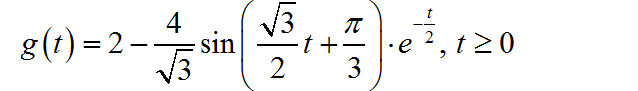
下面利用 LTspice 对该电路进行仿真,将仿真结果与上面计算公式进行对比。
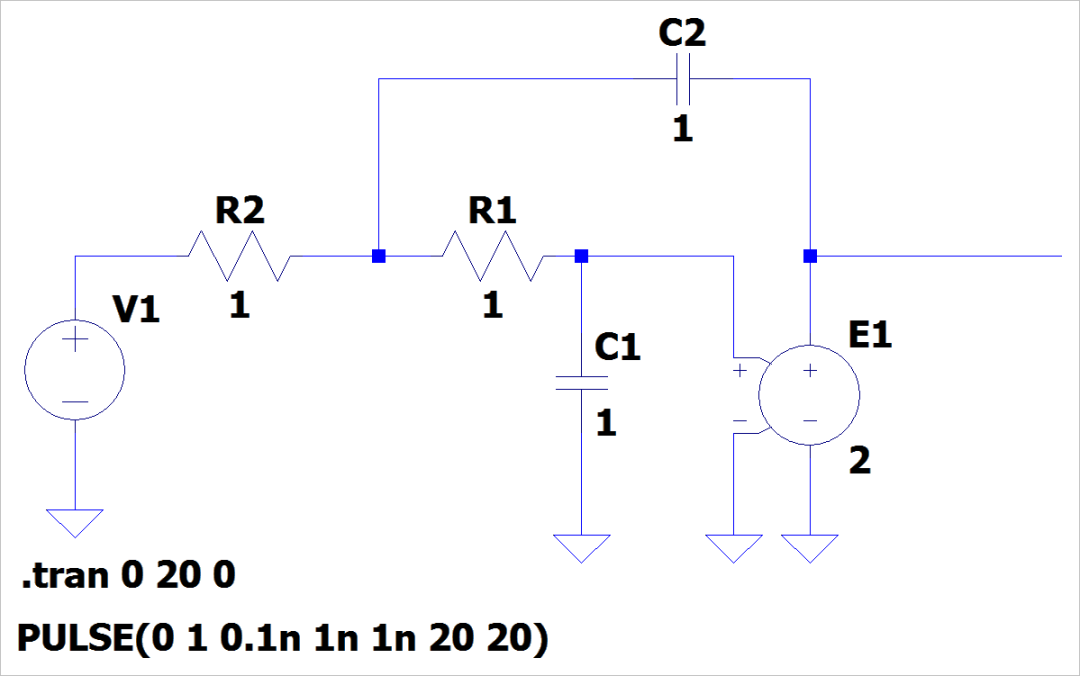
▲ 图1.5.2 利用 LTspice仿真电路电路的单位阶跃响应如下图所示。可以看到仿真与计算结果绘制的曲线是一样的。从而验证了上述答案的正确性。
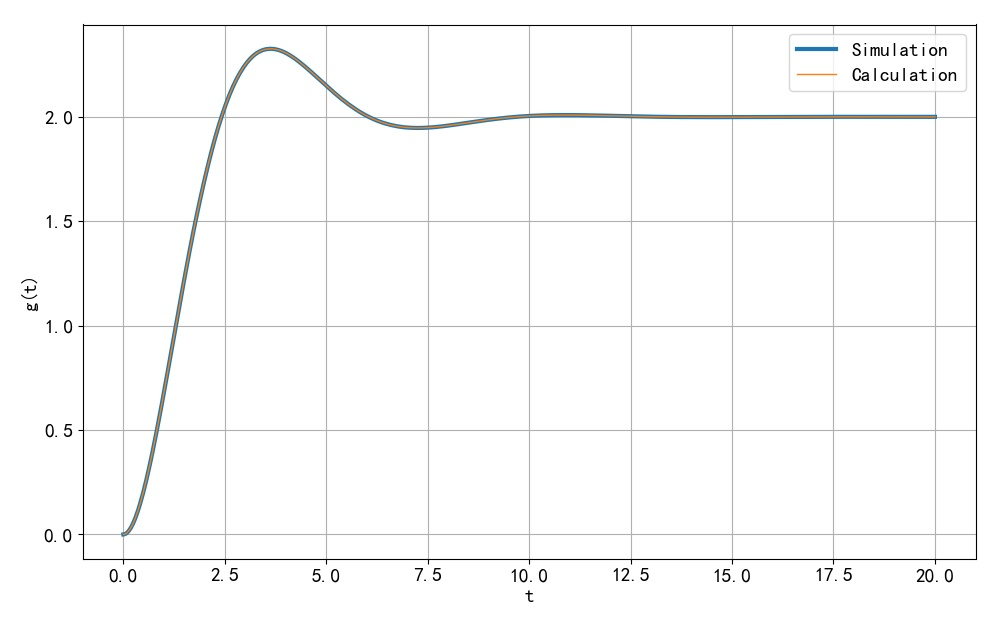
▲ 图1.5.4 仿真与计算曲线
□ 解答:
1、根据系统是因果、稳定、LTI系统,可以知道系统的有利系统函数的极点都位于 s 平面的左半平面。
2、根据系统在 的左腋下,系统的输出为加v对可积,表明 的有炼狱包含着虚轴,即 没有 出的极点,所以 至少包含有一个 的零点。
3、根据系统在 的作用下,系统的输出不是绝对可积,因此, 在 处的零点不超过两阶,所以系统函数可以写成:

4、根据 ${{d2 } \over {dt2 }}h\left( t \right) + 3{d \over {dt}}h\left( t \right) + 2\left( {s2 3s + 2} \right)H\left( s \right)B\left( s \right) = s2 3s + 2$ 。
5、根据 在无穷远点只有一个一阶零点,说明 的分子比分母阶次小于 1,所以系统函数可以写成:

6、根据 ,可以求得:
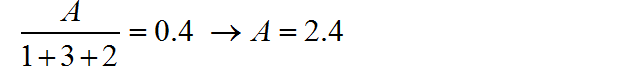
最终,该系统的系统函数为:

系统具有两个极点,分别为: 。根据系统为因果系统,所以系统函数的收敛域为: 。

□ 解答:
将 进行 Laplace 变换:
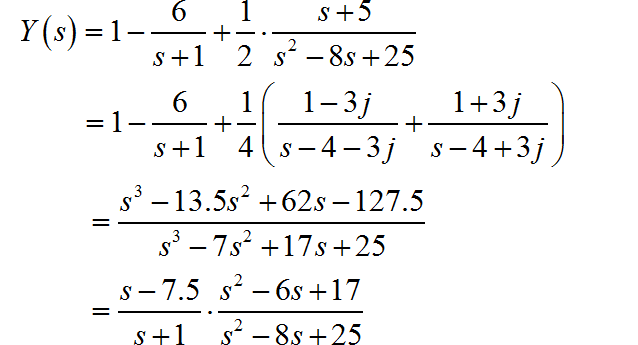
由于 是实数函数,所以 应该包含有共轭函数:
 所以:
所以:
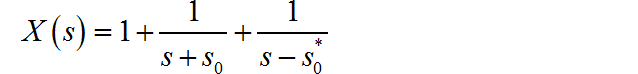
对比LTI输出信号的表达式,可以知道 。
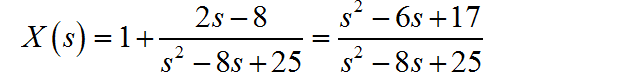
因为
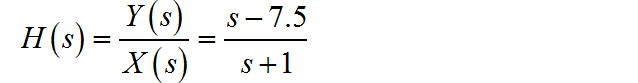
信号与系统2024(春季)作业要求以及参考答案汇总: https://zhuoqing.blog.csdn.net/article/details/136798840
[2]信号与系统2024(春季)作业要求 - 第十二次作业: https://zhuoqing.blog.csdn.net/article/details/139134081