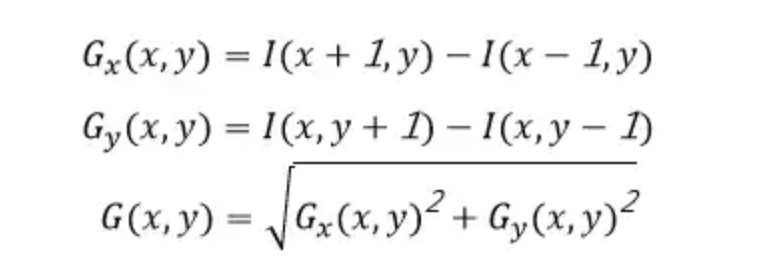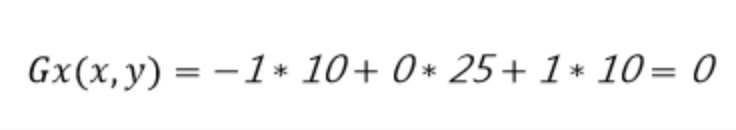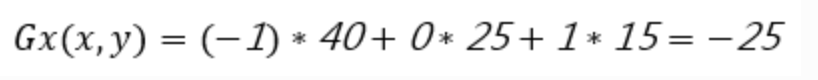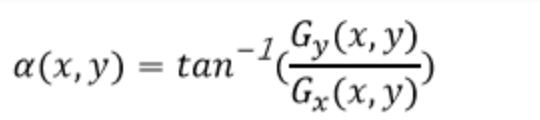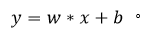图源:Zapp2Photo/ShutterStock.com
车辆检测技术看似神秘,本质上是通过数学公式,计算出图片上指定区域内的像素特征,进而根据特征判断物体所属类别。物体检测方法可以总结为特征提取与类别判定两步,常用方法为支持向量机,(Support Vector Machine,SVM)与方向梯度直方图(Histograms of Oriented Gradients,HOG)相互配合。
本文将从以下几个方面介绍这种常用的车辆检测算法,揭开其神秘面纱,也让读者通过阅读对机器学习过程有清晰的了解。
现实生活中车辆检测技术应用广泛,下面举例说明车内装置的应用。我们平时开的私家车里有时会有后置车载摄像头,后方一定距离内有车将要超过该车时,此系统便会启动,检测出后方车辆以后发出警报,提示驾驶员减速驾驶(
图1
)。另一个例子便是在自动驾驶领域的应用,通过对周边车的定位,分析他车车速、距离等干扰因素,从而改变该车的行驶轨道。
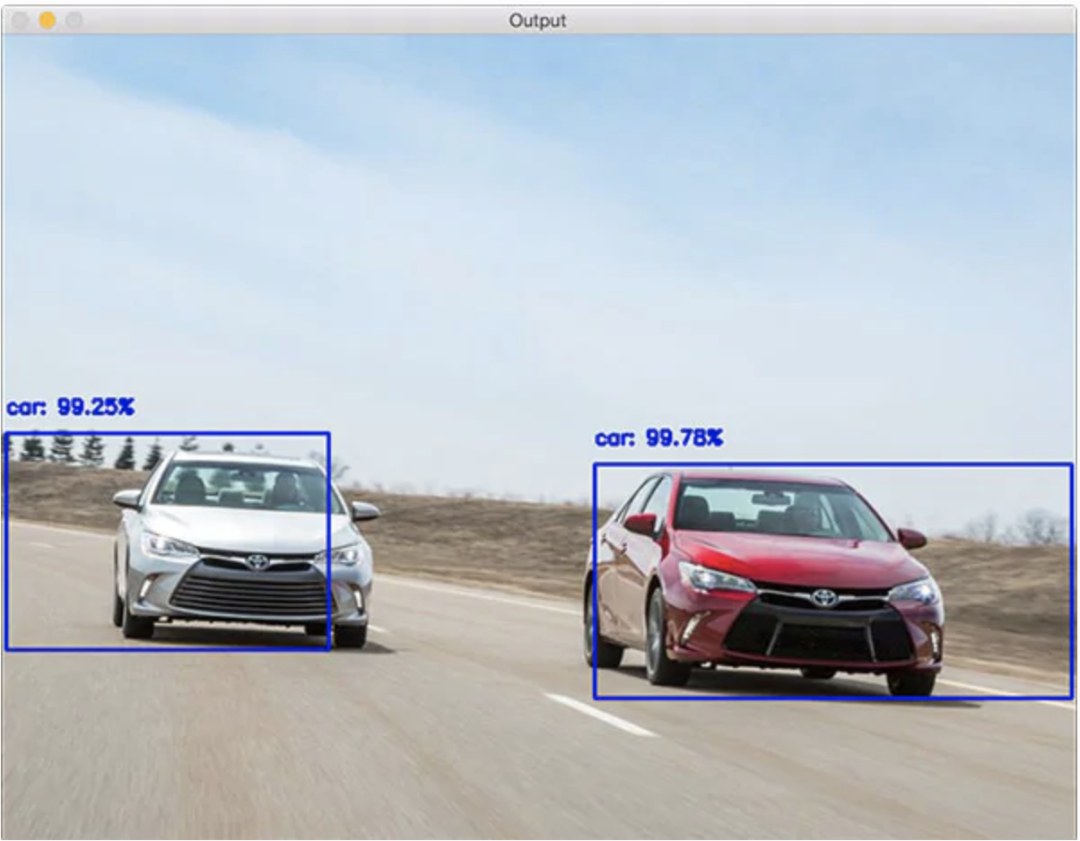
图1:后视车载摄像头检测出车辆并在图像上用矩形框定位
车辆检测系统还广泛用于交通管制和路况监控(
图2
),例如在隧道口安置此系统,就可以统计每天各个时段的车流量,适当实施限行政策,减少交通事故的发生,并且提醒驾驶员哪里是拥挤路段、哪里交通较为顺畅,进而方便驾驶员选择出行线路,起到疏散交通的目的。此外车流量的统计也会应用在机场或火车站的停车场,经过大数据分析出车位紧张的时段,以便工作人员合理调度资源。
附带车辆检测系统的信号灯可以通过与其他技术相结合,探测信号灯周围车流量,并由工作人员通过大数据人工智能进行统计,通过计算设定红绿灯交替变换的合理时间间隔。
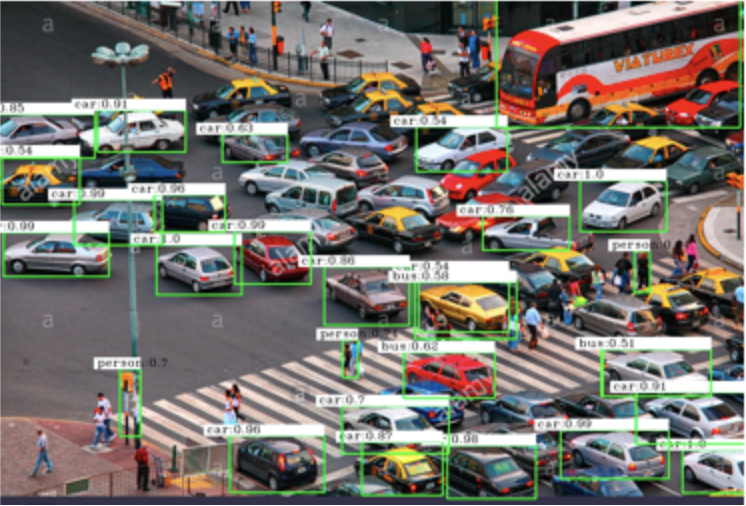
图2:车辆检测系统在路况监控场景下的应用
HOG与SVM相结合的算法:(40−16)/8+1=4
利用HOG与SVM相结合的行人检测方法最初是由法国研究人员Dalal于2005年在CVPR上提出的,如今演变成以HOG+SVM为主要思路对各类物体进行检测,包括车辆以及车道的定位。
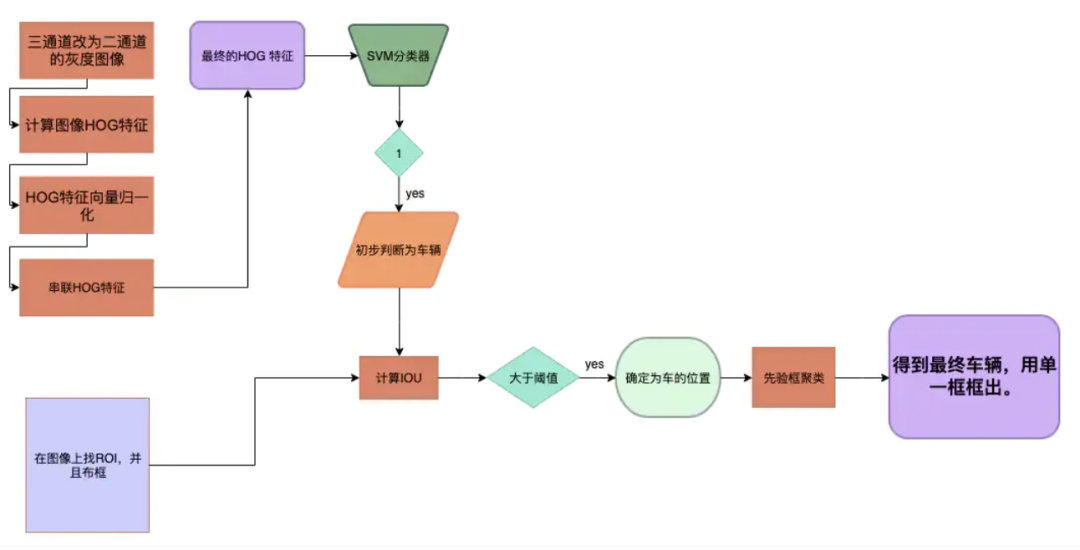
图3:SVM与HOG结合做车辆检测的流程图
1. HOG是一个局部提取特征的算法。如果是包含复杂背景的大图,就算提取再多的特征也达不到检测物体的目的。我们需要将图片剪裁得到目标。经实验证明,车辆作为目标物体占图片比重必须大于80%才会得到好的效果。在剪裁好的局部图像上将图像分区(block),每个区域以细胞(cell)为单位提取特征。(图像中的多个像素为一个细胞cell,多个cell组成区域块block。)我们以
图4
为例,解释HOG特征的计算过程。首先剪裁得到一张40*40的图片(以像素为单位),之后我们要定义如下几个变量:
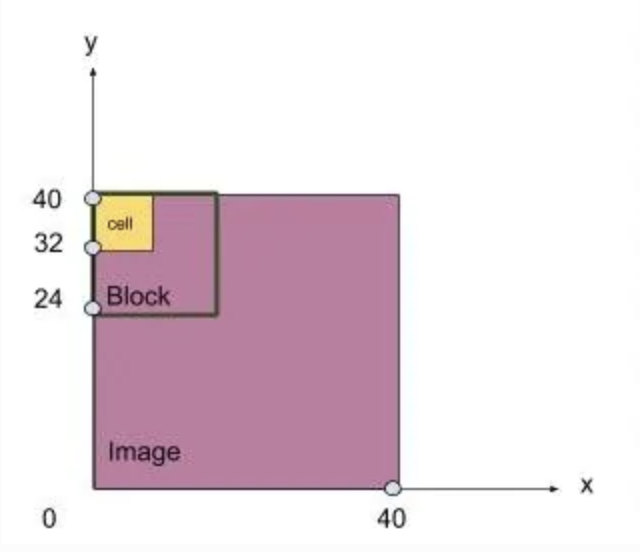
图4:block在剪裁图片上的移动过程,由图可知4个cell组成一个边长为16个像素的block,图片经剪裁得到长宽均为40个像素值。步长为1,即每次移动一个像素值
-
-
-
定义block大小,例如:由2*2=4个cell组成。
定义bin的数量取值,根据需要设定数量,例如bin=9,每个bin用来存放计算出的直方图的梯度方向累加值,其原理下文将具体讲解。
2. 对输入的图像及颜色进行标准化处理,减少光照或阴影对图像中物体检测准确性的干扰,具体做法是进行gemma颜色矫正后改为灰度图(Gemma颜色矫正原理在此不做介绍)。
3. 梯度大小的计算。以一个细胞部分区域为例做计算方法讲解(图5),下文为计算像素值为25的中间点的公式。
采用一个合理的卷积核方式的定义,实验表明[-1,0,1]效果最好。卷积核[-1,0,1]可以理解为一个矩阵,用于计算每个像素点的梯度幅值方向,因此我们可以横向(x轴正方向,向右)采用[-1,0,1]的卷积核,纵向(y轴正方向,向上)采用[-1,0,1]T,对于图像区域中的每一个像素点做横向、纵向的梯度分量计算,二者平方和开根号得到该点的梯度方向,因此计算公式如下:
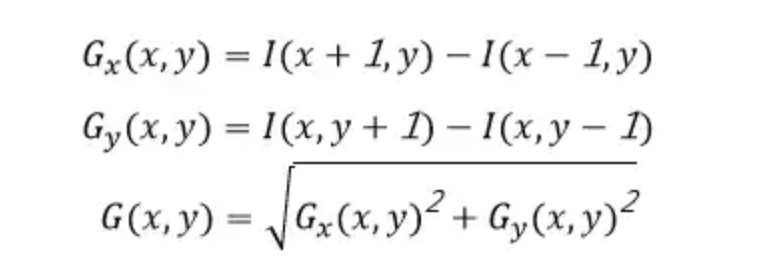
所以像素为25的点水平方向的计算方法如下(
图6
)所示:
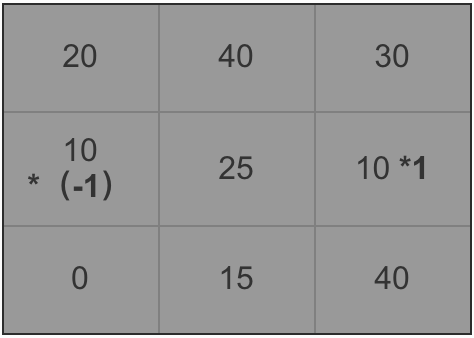
图6:像素值为25的中间点水平方向的像素值的计算过程
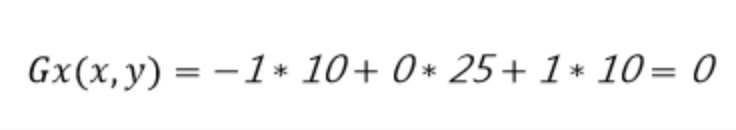
所以像素为25的点垂直方向计算方法如下(图7)所示:
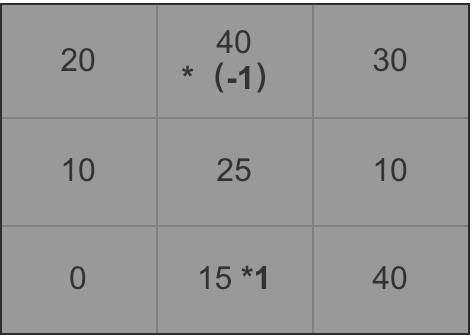
图7:像素值为25的中间点水平方向的像素值的计算过程
5. 对每个细胞(cell)中的所有像素点重复3-4的计算过程,再将数值相加,我们就得到了一个细胞(cell)内9个梯度方向上的梯度积分图(
图8
)。
6. 求解图像分区(block)的HOG特征,即:将所包含的细胞(cell)特征串联到一起。
7. 求解整个图片的HOG特征,即:将所包含的图像分区(block)特征串联到一起。
以上例子中block块沿着x,y轴分别移动4步:
(40-16)/ 8+1 = 4
每个block中包含4个cell:
2 * 2 = 4
特征维度的计算公式:
(2*2)*((40-16)/8+1)2* bin =4*16*9=576
9. 将求得的梯度向量正则化。正则化的重要目的是为了防止过拟合。过拟合会造成对训练集的分类效果过于理想,但是测试集检测率极其偏低,这显然是我们不能接受的。跟一般的机器学习特征正则化的道理相同,例如得到的特征值在(0,200)之间分布,我们要求防止200以内的数字对特征整体分布造成影响(模型在训练中会为了迎合200而偏离整体趋势,造成过拟合),因此要将特征分布规范化到一定区间。Dalal在论文中提到采用L2-norm得到的效果非常理想。(这里0,200指特征值所在的范围)
10. 将特征与标签一起送往SVM中对分类器进行训练。
直方图的梯度方向及bin的取值
Dalal在论文中提到,“这一步骤的目的是为局部图像区域提供一个指示函数量化梯度方向的同时,能够保持对图像中检测对象外观的弱敏感性”。梯度大小要根据梯度方向插入到对应的bin中,方向分为两种。第一种是无方向的方法(unsighed),适用于车辆或其他目标检测;第二种是有方向的方法(sighed),经实验证明,不适用于车辆或其他目标检测,这种方法在图片放大、缩小、或经过旋转后,像素点要恢复到原位置时会有应用,可以点击参考文献的第5个链接进行深入了解。
本文将使用三张表格去做讲解,每张表格中第一行为计算出的幅值,第二行为规定好的bin的方向取值,由180度除以定义的bin个数得来。第三行为bin的序号,从0开始。
根据实际需要分成若干个bin,例如分成9个,即每个细胞内统计9个方向的梯度直方图,每个bin的覆盖方向为20度。将幅值(上文中计算的G(x,y))插入到bin中,最终bin中幅值的累加和即为直方图的纵轴,横轴则是bin的取值范围,该例中取(0,8)的数字。
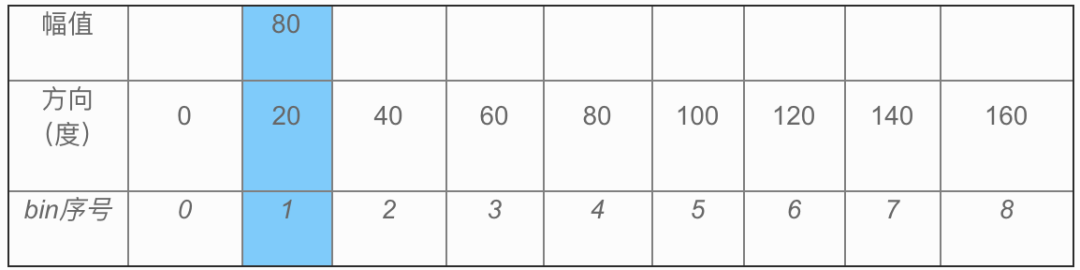
若某个像素点的幅值为80,方向为20度,则插入到(
表格1
)蓝色区域的位置:
若幅值为80,方向为10度,则分别插入到(表格2)蓝色填充的两个位置:
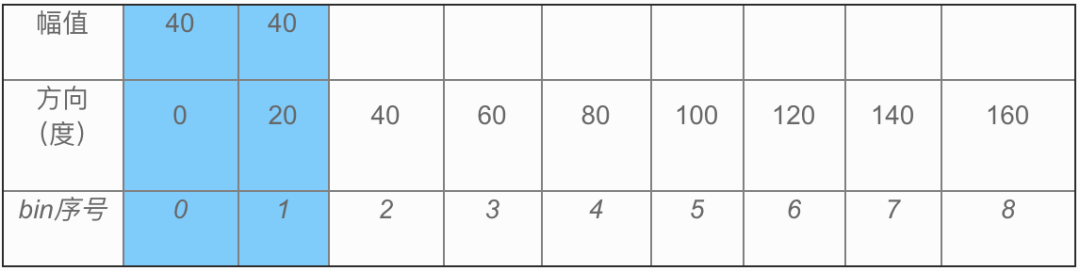
表格2
若幅值为60,方向为165度,则分别插入到表格3蓝色的两个位置:
(180度和0度在方向上等价,所以幅值按1:3分别插入两个bin)
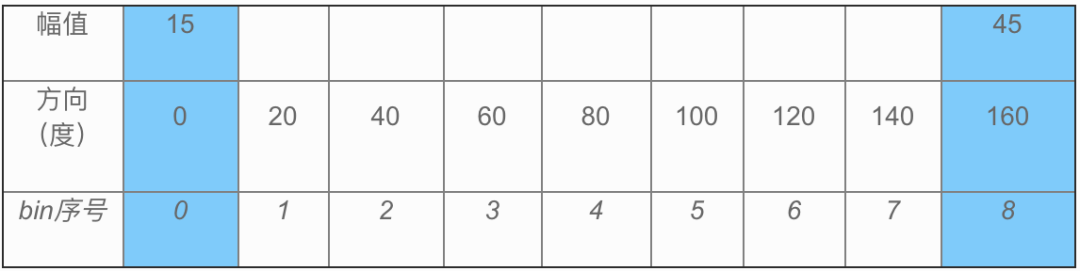
表格3
上述(
表格1
)介绍的方向值恰好为bin对应值的插入方法,表格2介绍了方向值介于两个bin值之间的插入方法,表格3介绍了方向值大于最大bin值的插入方法。根据三种方法的原理,以cell为单位计算,一个cell中所有像素点遍历后的幅值累加,例如上面我们在0号bin的位置得到了两个幅度值分别为40和15,因此我们到目前为止0号bin的直方图累加到55。以此类推,计算每个cell的1-8号bin幅度并分别累加。最终我们会得到类似于下面(
图8
)的直方图,其中横坐标X为梯度方向,纵坐标Y为梯度幅值:
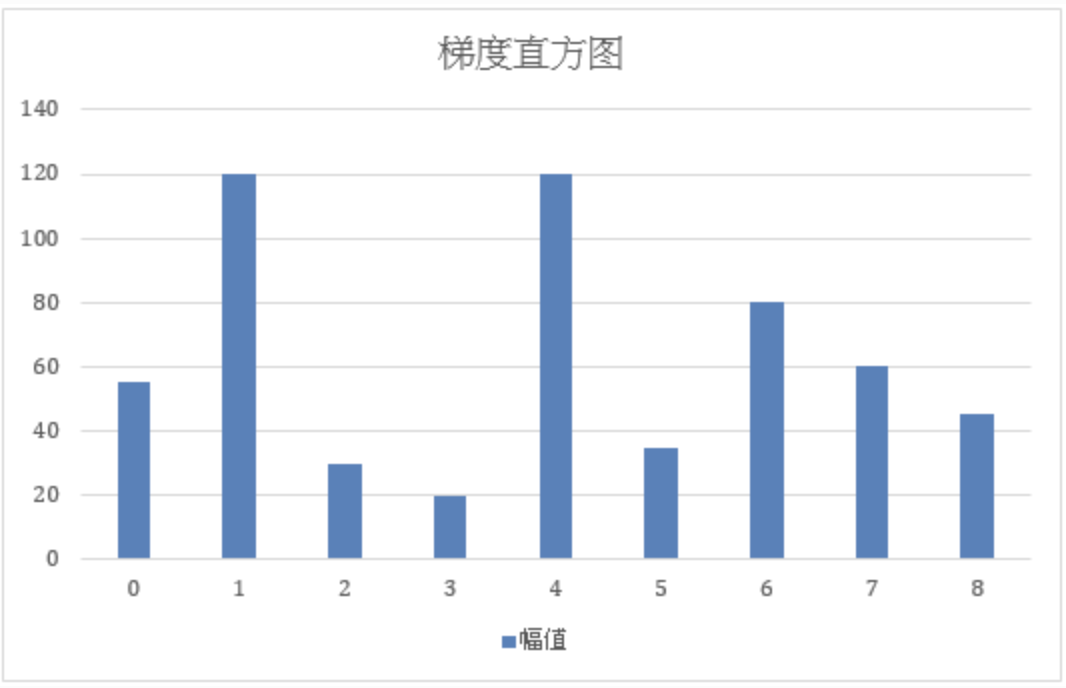
图8:梯度直方图实例。横轴为bin序号,纵轴为计算出的幅值。本图纵轴对应的数字仅为举例说明,例如,上方三张表格中的bin1幅值加和得到80+40+0=120作为最终结果,则直方图纵坐标得到120,继续做计算,bin1的值会继续累加。
实验证明目标检测时用9个bin,单向插入会得到最佳效果。
方向前加了正负号,若也定义9个bin,则每一个bin所分配到的角度范围是(0,π/9°)。例如,第二个bin的正值插入到20-40度的bin(蓝色的扇形区域),负值应插入到200-220度的bin中(蓝色的扇形区域)。(
图9
)
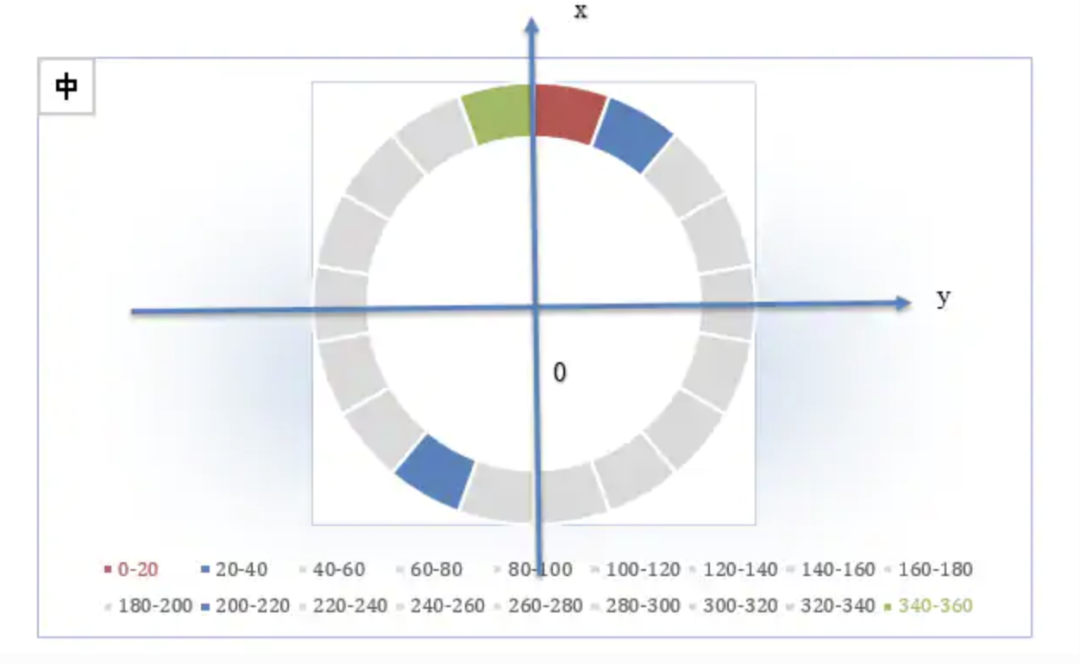
图9:有方向的插值方法,每一个扇形区域代表一个bin覆盖角度范围值。红色为一号bin,覆盖0-20度。顺时针方向依次标号,绿色为终点,340-360度。蓝色区域为相对应的两个方向的bin.
SVM(Support Vector Machine)全称为支持向量机,在空间中就是将两个类别通过一个超平面分开,在二维空间可简单理解成为了找到y而y满足:
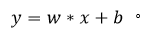
y的值决定了样本是正类还是负类。但是如何确定最优超平面,这里就引入了支持向量和最大间隔。我们的目标是引入超平面,使得距离超平面最近的点之间有最大间隔(图10)。
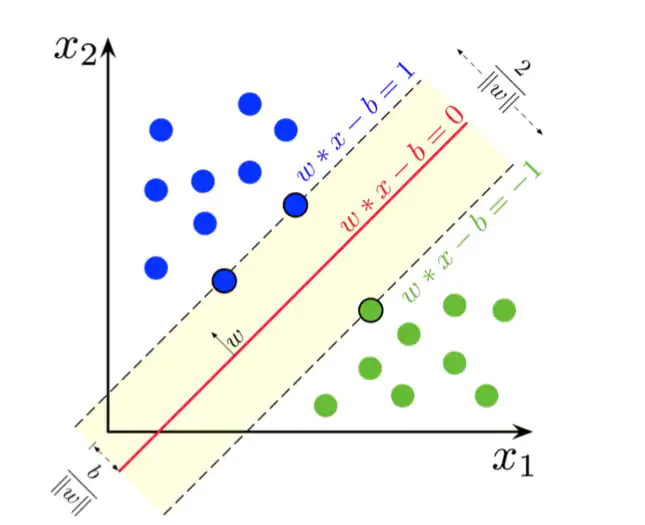
图10:红色的线为超平面,落在两侧的虚线上的点为支持向量,计算得到的