在信号处理领域,经常会提到两个名词-线性相位与群延迟,那么,什么是线性相位?什么是群延迟?二者之间又有什么关系呢?
一、理论原理
1、线性相位
对于线性时不变系统,其频率响应包含两部分:幅频响应与相频响应,幅频响应描述系统输出信号幅度与频率的关系,相频响应描述系统输出信号相移与频率的关系,如果相移与频率呈线性关系,则系统具备线性相位特性。
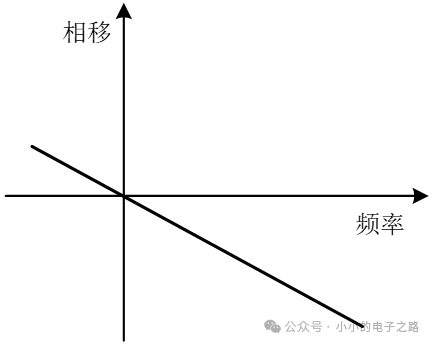
2、群延迟
单一频率信号没有群延迟的概念,群延迟是针对由不同频率信号组成的合成信号而言的,描述的是系统对输入的合成信号中不同频率信号的时延。
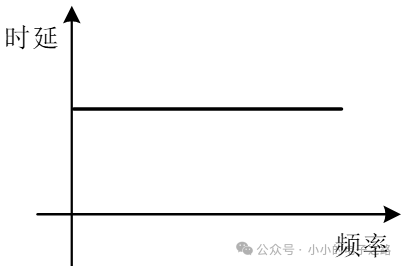
3、线性相位与群延迟
相频响应与群延迟之间的关系的公式描述为
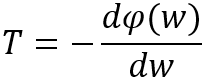
若系统具备线性相位特性,则其群延迟T为常量。
举例说明:
对于一个合成信号,其所有频率成分可由一个公式表示,即:
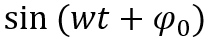
如果系统的群延迟是一个常量T,则其输出信号为:
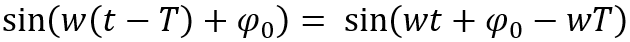
该合成信号中各个频率分量的相移
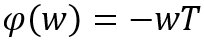
该相移与频率呈线性关系,系统具备线性相位特性,因此,当系统对输入信号所有频率分量的延迟都相同时,即群延迟为常量时,系统为线性相位系统。
反之,如果系统的群延迟与频率相关,为T(w),则其输出信号为:

该合成信号中各个频率分量的相移
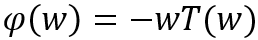
此时相移与频率并非线性关系,该系统不具备线性相位特性。
二、仿真分析
如果系统不具备线性相位特性,会带来什么危害呢?下面通过仿真来看一下。
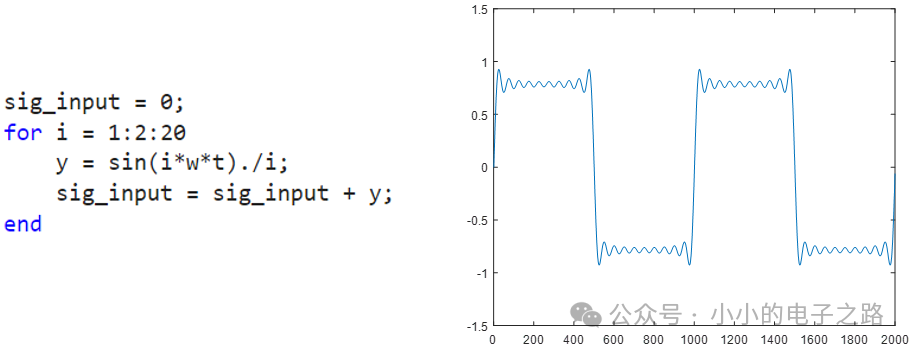
1、输入信号
先看输入信号的波形,输入信号是由多个正弦波合成的方波信号,基波频率为1Hz。
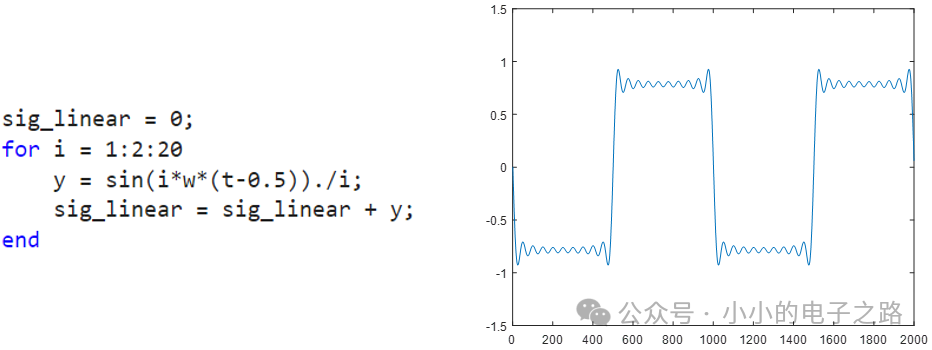
2、线性相位
如果系统具备线性相位特性,即群延迟为常量,仿真中设置为0.5s,则输出波形相较于输入波形只是产生了0.5s的时延,波形并未发生失真。
3、非线性相位
反之,如果系统不具备线性相位特性,即群延迟和频率相关,仿真中10Hz及以下频率信号的时延设置为0.5s,10Hz以上频率信号的时延设置为0.6s,则相较于输入信号,输出信号发生了明显的波形失真。

因此,可以得出结论:线性相位是保证信号无失真传输的条件之一。