我们前面分享了两篇文章, 从头脑风暴,纯思想实验出发,引出了PDM以及sigma-deleta的原理。如果读者有心,仔细去回味,思考,可能会举一反三,发现实践中很多场景可以应用类似的思想,其实这是一类问题,一通则百通。
如果没有,那么看完本文, 希望能有。看完你可能会拍案而起,或者激动的拍大腿,这也是本人希望分享技术文章的初衷,希望能让读者读到欲罢不能甚至有激动兴奋的感觉。本文重点还是一如既往的希望授人以渔,而不是单纯的输出一个技术点。
https://mp.weixin.qq.com/s/9Vhe1rUCI8ZGBGGy3todcw PDM系列文章之二:一文搞懂PDM编码基本原理1bit sigma-deleta ADC,
https://mp.weixin.qq.com/s/uuKljd3zPjj-gkrjlvWEbg PDM系列文章之一- 前菜篇,假如来发明我们自己的PDM
这个问题是一个读者私下问我的一个问题,即我们在音视频处理中”生产者”和”消费者”可能速率不匹配,比如视频采集帧率很快,但是视频编解码可能达不到采集的帧率需要降帧率处理。对于降帧比是整数倍的很好解决,就是指定帧数处理一帧就行,比如输入10FPS需要降帧率到5FPS处理,那么就是每两帧丢掉一帧即可。那么如果不是整数倍数的降帧率呢,比如输出10FPS要按照3FPS处理,算法如何实现?
说实话我之前也没有写过该算法,但是看到这个问题,我一秒钟就想到了我们之前讨论过的PDM的原理。我们还是按照之前文章提出的思路,先抽象,再分析。这个问题题干很简单,简单描述就是对帧率为xFPS的输入,如何挑选丢弃一些帧得到更小的帧率yFPS,当然要保证均匀性。我们进一步抽象,按照之前设计自己的PDM的思路进行,先对输入对象抽象,输入对象就是帧流,我们可以每一帧用1表示,那么输入就是11111的流,而输出是对11111流的挑选是否需要进行处理,如果需要对输入进行处理就输出1,不需要处理就输出0。那么结果就是10的序列编码输出。那么问题就抽象为了如何对输入流11xxxx,通过挑选使得其输出流10xxxxx,满足1均匀分布,且1的比例(密度)正好是指定的倍数。原来1的密度认为是100%,那么降低帧率倍数为x,那么输出的1的密度就是原来的1/x.
我们再来看抽象后的模型不就是我们的PDM编码吗? 用1的密度代表帧率,之前引出PDM时是用1的密度代表电压,所以不管是代表电压还是代表帧率还是代表什么妖魔鬼怪,都是一样的问题,对于抽象或者数学上来说就是一个数字。所以再次说明我们之前提出的,解决问题的第一步是抽象这一重要观点。
如果读者看过之前两篇文章,且确实是用心去思考理解过的话,到此为此,应该就要拍大腿,激动的说哦原来如此了,所以实际本文至此就可以结束了。但是我们还是善始善终,还是把整个实现过程分享一下。
为了方便编码,我们还是回忆下sigma-deleta的系统框图, 把我们的问题抽象后,映射到模型上,图像化,才能方便实现。
典型的1bit sigam-delta系统框图如下,由一个差分模块(计算本次偏差),积分模块(计算累计误差),和一个比较模块-DAC输出模块(负反馈)组成。如下所示,DAC输出实际是一个开关控制输出,要么输出VREF参考电压,要么输出0,参考电压VREF大于Xi输入电压,开关的控制由比较器决定,比较器的输出由误差的累计决定,也就是说有正向误差则控制DAC输出VREF,此时Xi
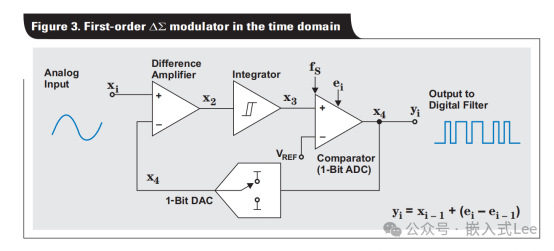
不说什么高深的概念,四个字就可以说明其核心思想,多退少补! 多了往少的方向调整,少了往多的方向调整。
移植到我们降低帧率的问题来看,DAC的输出即参考电压VREF对应的是输入帧率,需要对其进行不断的开关开关(即10xxx序列),最终使得其等效为输出帧率Xi(即待采样电压)。
积分器的输出就是实时的误差,DAC的开关序列即帧的挑选序列。
好了有了以上的模型说明,编码其实很简单了
几行就搞定,只需要简单的加减法即可,非常高效
/*** \struct sigma_delta_st* sigma_delta结构体*/typedef struct{int input; /**< 输入值(参考值) */int output; /**< 目标值 */int integrator; /**< 积分器输出 */int dac; /**< 比较器输出, 0表示DAC无需输出参考值,1表示DAC需要输出参考值 */} sigma_delta_st;/*** \fn sigma_delta_init* 初始化* \param dev 用户提供的实例, \ref sigma_delta_st* \param input 输入值(参考值)* \param output 目标值*/static void sigma_delta_init(sigma_delta_st* dev, int input, int output){if(dev == (sigma_delta_st*)0){return;}dev->dac = 0; /**< 初始时DAC无输出,初始积分器偏差为0-output */dev->integrator = 0-output;dev->input = input;dev->output = output;}/*** \fn sigma_delta_update* 计算下一步1bit DAC是否输出, 1输出, 0不输出* 反复调用本函数反复输出10序列,10序列即input的开关序列,其平均效果等效于目标output的值.* \param dev 用户提供的实例, \ref sigma_delta_st* \return 返回1或者0,即DAC的输出开关,1表示输出,0表示不输出*/static int sigma_delta_update(sigma_delta_st* dev){if(dev == (sigma_delta_st*)0){return 0;}/* (偏差)积分值,经过比较器(和0比较),确认偏差的正负方向,然后控制DAC输出反向调整积分值,形成负反馈* 目标是让积分器的输出趋于0,即偏差趋于0,即差分输入正负输出等效,即output和input的开关序列等效*/if(dev->integrator > 0){/* 如果积分值大于0, 则DAC使能输出,即输出input差分输入dev->output-dev->input小于0,使得积分值减小,反向调整积分值*/dev->dac = 1;dev->integrator += dev->output-dev->input;}else{/* 如果积分值小于等于0, 则DAC停止输出,即输出0差分输入dev->output-0大于0,使得积分值增大,反向调整积分值*/dev->dac = 0;dev->integrator += (dev->output-0);}return dev->dac;}
测试代码如下
/*** \fn sigma_delta_test* 测试函数* \param[in] input 输入值* \param[in] input 输出值* \param[in] pnum 更新次数*/static void sigma_delta_test(int input, int output, int pnum){sigma_delta_st dev;sigma_delta_init(&dev, input, output);printf("\r\n");while(pnum--){int res = sigma_delta_update(&dev);printf("%d %d %d\r\n",res,dev.input,dev.integrator);os_delay(10);}}
我们实现命令行方便测试
void sdtestfunc(uint8_t* param){int input;int output;int pnum;if(3 == sscanf((const char*)param, "%*s %d %d %d", &input, &output, &pnum)){sigma_delta_test(input,output,pnum);}}
测试不同的降采样率比例,打印挑选序列
10:8降采样率,第一列为抽取序列1表示输出0表示丢弃,第三列表示当前偏差,可以看到任意5个中有4个1,正好是10:8
sh>
sdtest 10 8 20
0 10 0
0 10 8
1 10 6
1 10 4
1 10 2
1 10 0
0 10 8
1 10 6
1 10 4
1 10 2
1 10 0
0 10 8
1 10 6
1 10 4
1 10 2
1 10 0
10:3降采样率,第一列为抽取序列1表示输出0表示丢弃,第三列表示当前偏差,可以看到任意10个中有3个1,正好是10:3
sh>
sdtest 10 3 20
0 10 0
0 10 3
1 10 -4
0 10 -1
0 10 2
1 10 -5
0 10 -2
0 10 1
1 10 -6
0 10 -3
0 10 0
0 10 3
1 10 -4
0 10 -1
0 10 2
1 10 -5
0 10 -2
0 10 1
1 10 -6
0 10 -3
可以看到满足均匀输出,且抽取比例符合需求,当然可能存在偶尔一个窗口内有偏差的情况,因为输出只能是要么输出input要么输出0,颗粒度不是无限小,所以从长期时间平均才能更高精度等效,时间越长精度越高,这也是sigma-deleta ADC精度高但是需要采样时间长的原因,即时间换精度。
我们还是保持刨根问题和发散思维的精神,上述说的是降采样率,那么问题来了,如何升采样率呢,即对低采样率进行插值得到高采样率呢。我们要有逆向思考的思维,升采样率还是一回事,我们就假设知道升采样率后的帧率,然后对其降采样率,那么输出1则表示是使用输入帧,输出0则表示该帧需要插值。
好的,看到上面是不是还意犹未尽,我们继续思考是不是还可以想到类似的系统?
理想运放?
负反馈系统?
DC-DC?
PID?
等等是不是都是类似的,实际上你在实践中会发现更多类似的系统。
其实我们从哲学的角度来考虑这个问题会更有深刻的认知,中国传统文化其实是提倡中庸之道的,你会发现古人的智慧,其实负反馈就是中庸之道,负反馈系统是真实世界最最常见的系统,为什么呢,因为其中庸之道,多了少点,少了多点,趋于中庸稳定。而正反馈系统,则会一直朝着一个方向发散最后失控,就好比宇宙来源于大爆炸,最终肯定还是会坍缩,重复下一次大爆炸, 反复不息....,做人,工作,生活又何尝不是如此呢。
所以以上全文技术点用一句三岁小孩都懂的话来总结,就是多了就少点,少了就多点,所以技术没有什么高深的,原理都很简单,而用一句话让不懂技术的人搞懂,也是评估你是不是真的懂的最好的标准,如果你需要用一大堆高深的术语公式去说明一个技术问题,那么说明你肯定没有真的搞懂。而我们学习一个技术也要思考其背后的思想,甚至从哲学层面去思考,而不是仅仅停留在技术表面。