这篇文章又是一篇随笔,不过更看上去是散装文学(不算文学),终于熬到这里了,这里的概念不像前面的理论,需要计算的那么多,但是数形结合的地方很多。
很多图都是马同学的,我买了课就拿来一用了~
下面是之前学的关于数学的文章:
矩阵乘法观点-几何含义
二阶导数标记问题
定积分-黎曼和的极限
统计学-随机变量
蒙特卡洛计算PI(距离公式)+蒙特卡洛计算定积分
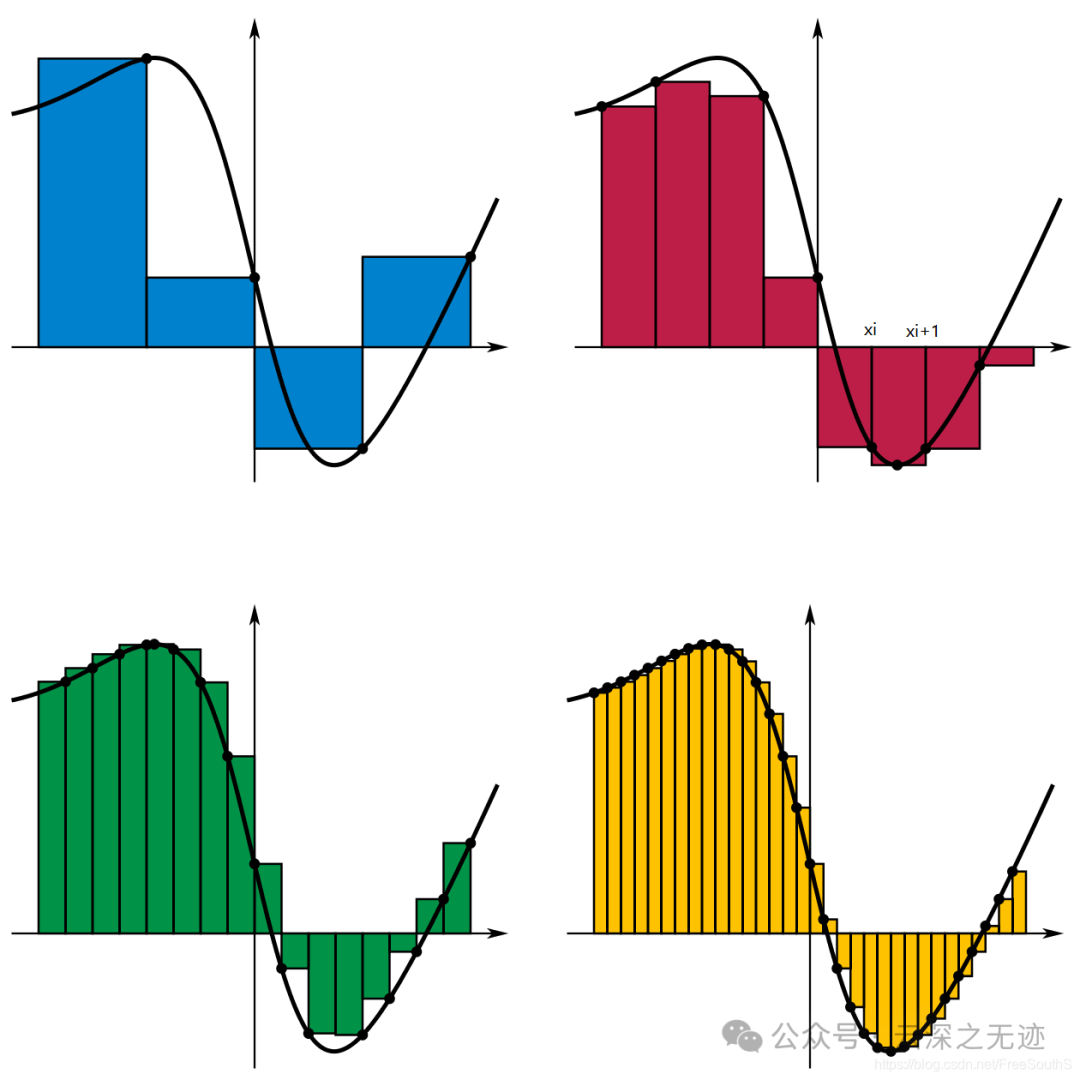
雷曼和:定积分就是黎曼和的极限
可积的充分条件:

这里补充什么样的原函数可以求积分
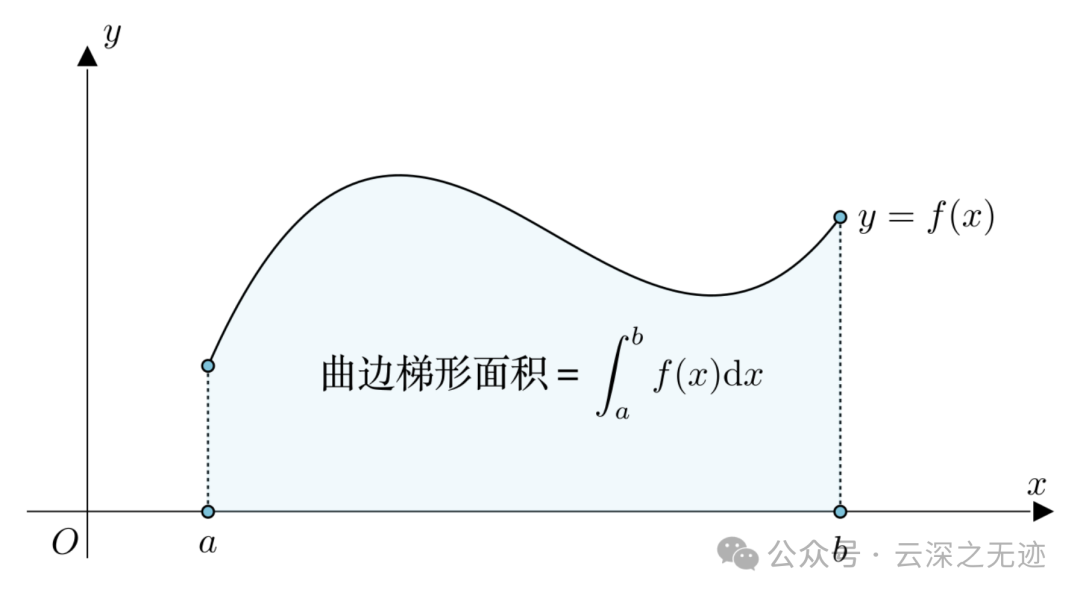
这样的就是最简单的可积,联系
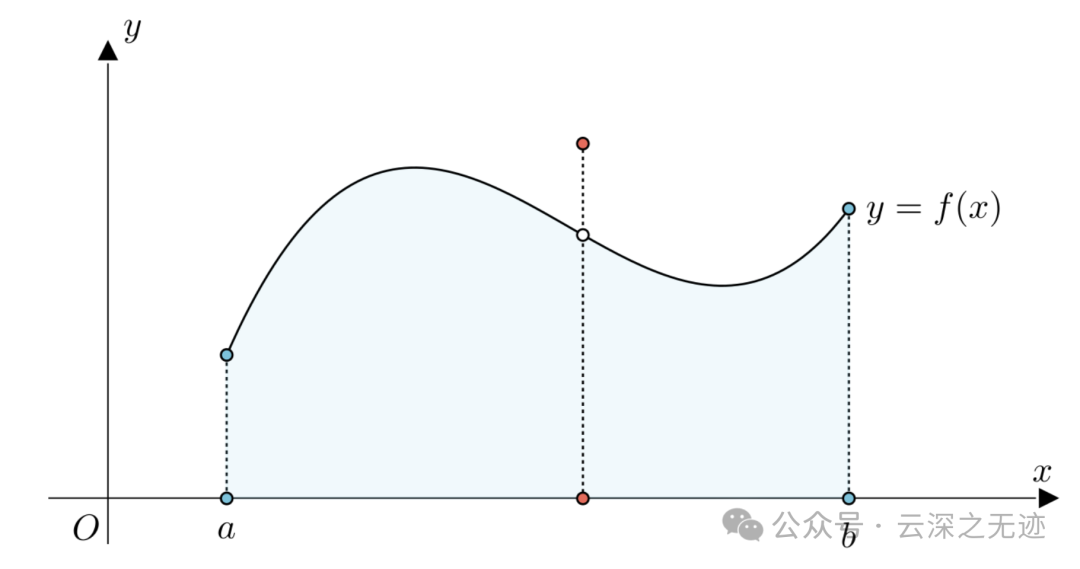
这里是有,有限个间断点,而且是可去,去了对面积没有影响

有两个跳跃点也是可以的

这样的点就是跳跃点,左右极限都有,但是不一样,第一类点
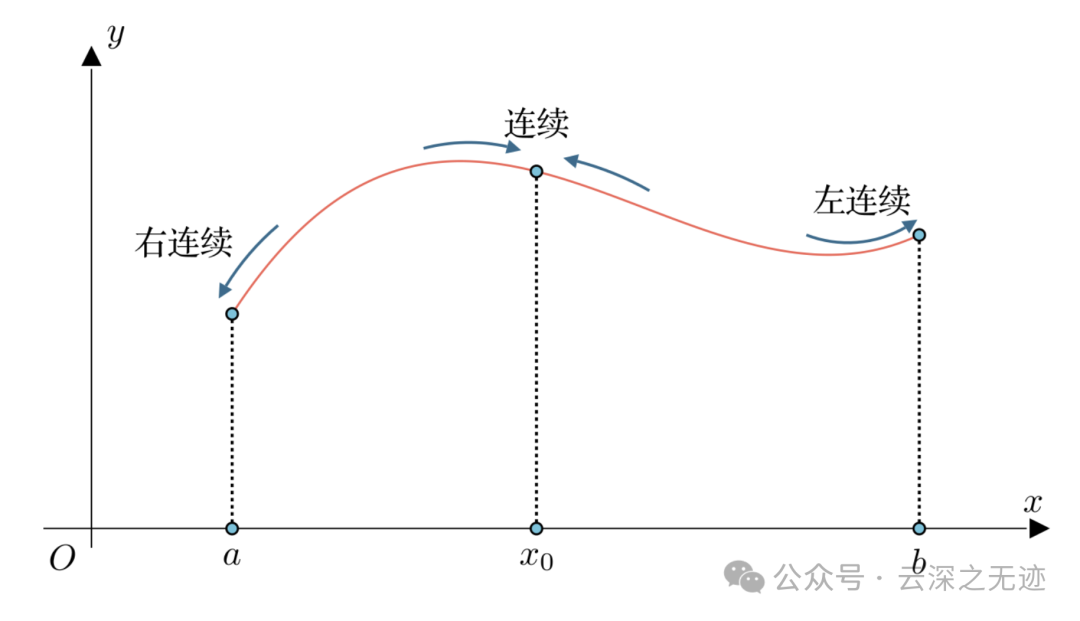
顺手引出了左右极限,就是在一个数字的左右做文章,其实最巧妙的就是0处,注意看图的箭头,我们一般说,在一个点的左边(位置),右连续,另外一面对称。
如果区间包括端点,那么函数在右端点连续就是指左连续,在左端点连续就是指右连续。这样的说法也是有条件的。

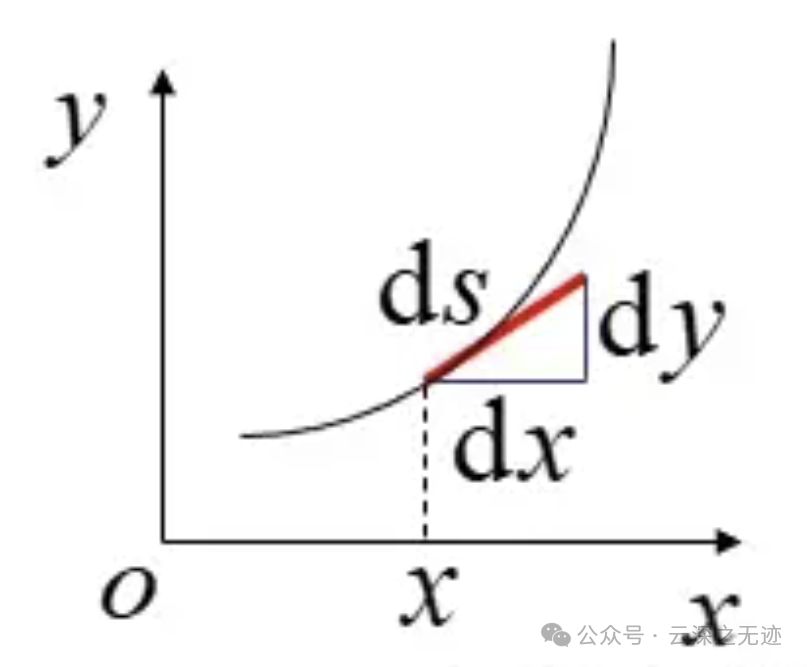
ds为弧微分
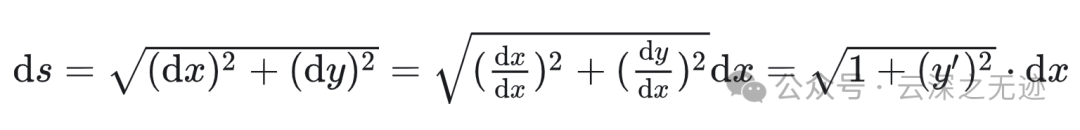
这个是一种最直观,但是不加证明的表达方式
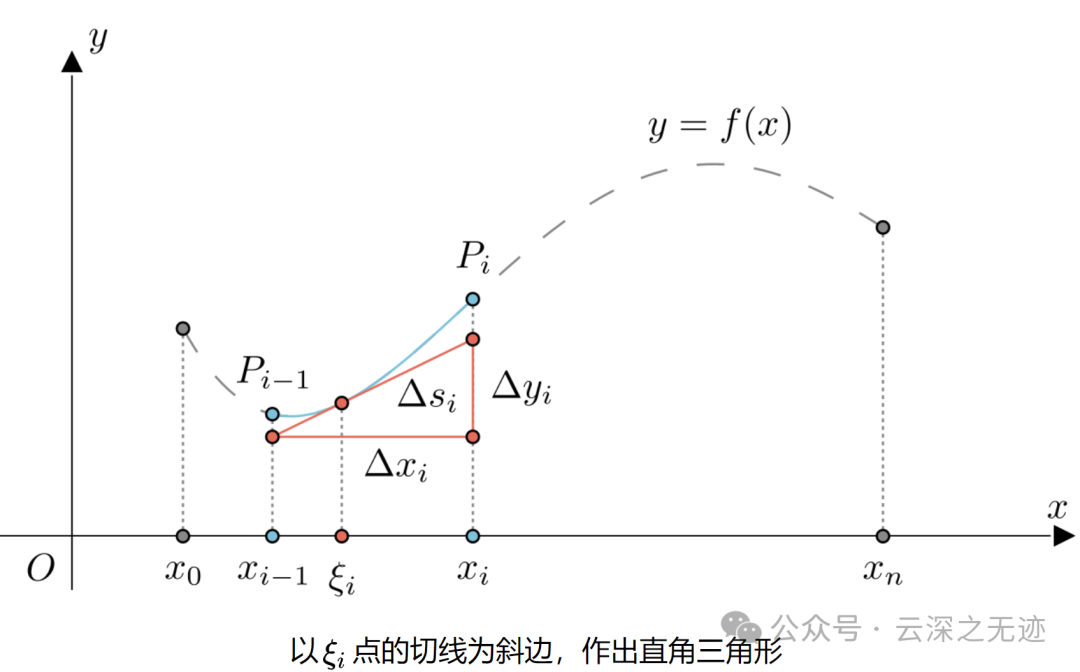
这样是放在整个曲线上面的直观证明

上面的笛卡尔坐标系,现在是参数坐标系

对于参数方程的求导是这样的,这里我想说的是反函数存在和求导的关系。
反函数不存在说明y不是X的函数,这里可能有些问题。
反函数有的地方还有这个:
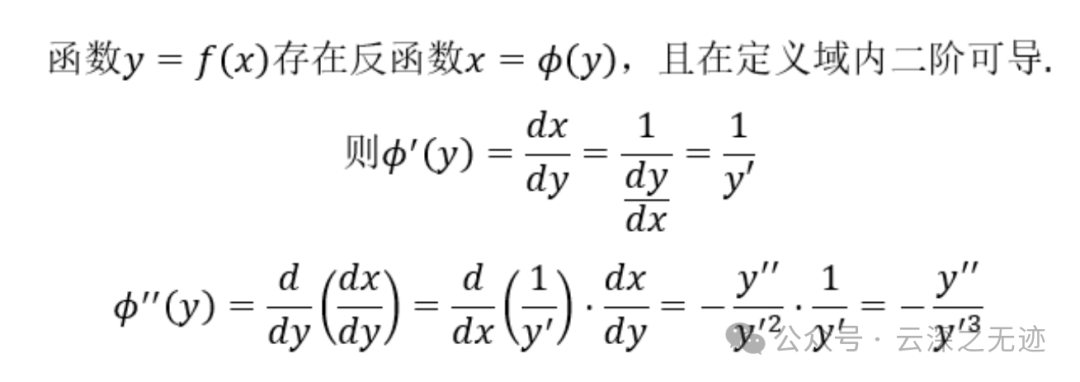
反函数求导,就是原导数分之一,还有二阶导的死样子
函数的微分(英语:Differential of a function)是指对函数的局部变化的一种线性描述。
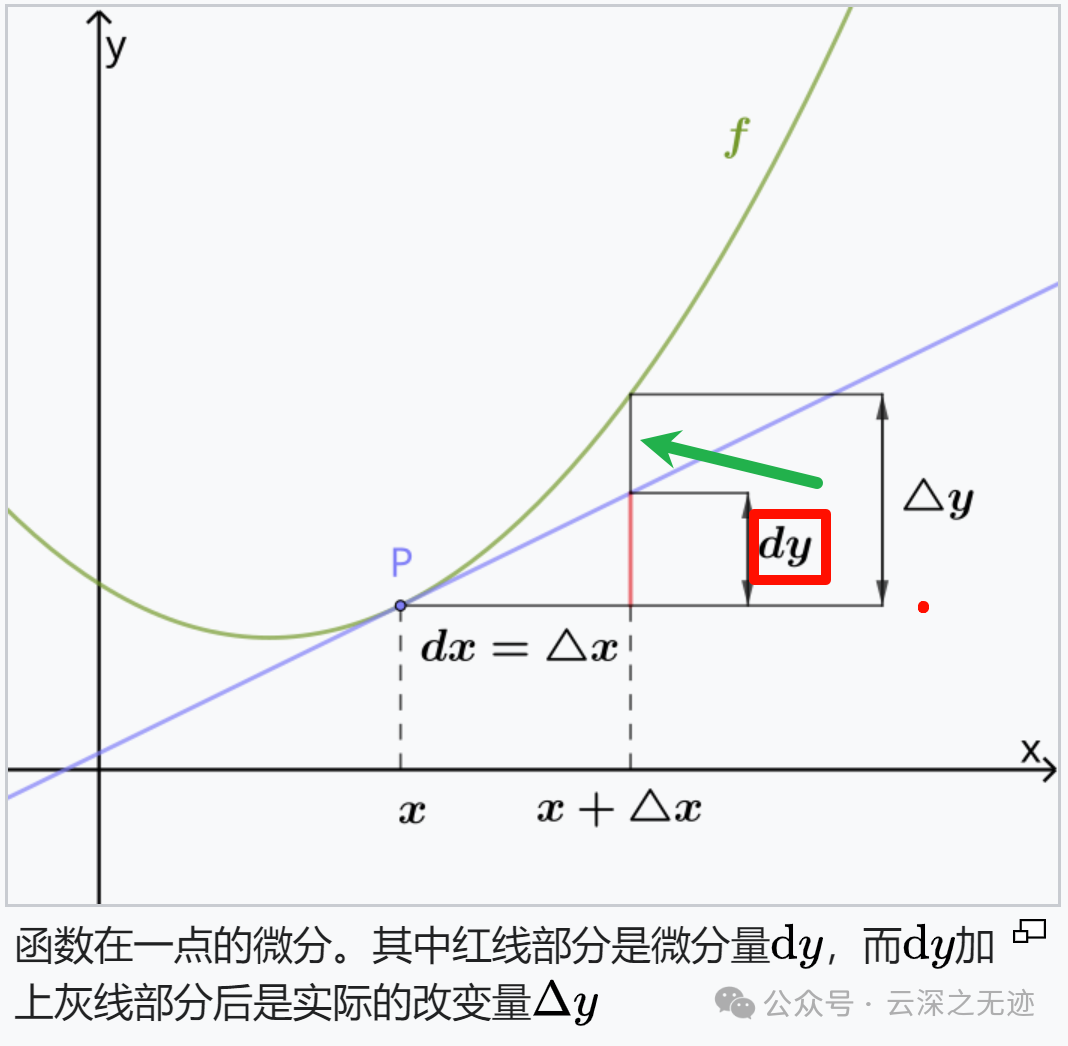
微分可以近似地描述当函数自变量的取值作足够小的改变时,函数的值是怎样改变的。
运放确实是做出了以前是做数学计算的,比如下面这个微分放大器:
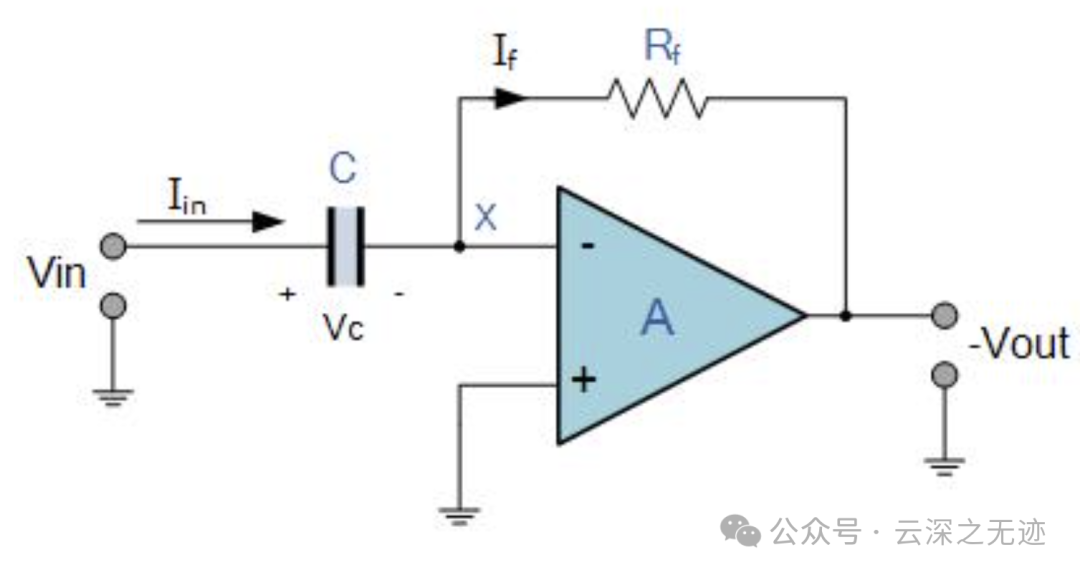
就是这样

就给sin求导,就是cos,最后一个,前面的我不会求导
输入电压信号的变化越快或越大,输入电流越大,响应时输出电压的变化就越大,形状越像“尖峰”。

使用弧长来推导⚪的曲率,也就是说曲率可以通过一维曲率公式(即弧长除以弧长上的距离)计算。

代码就是这样写
曲率(英语:curvature)即“弯曲度”,是描述几何体弯曲程度的量;直观地说,曲率是曲线偏离直线的量(程度),或是曲面偏离平面的量(程度)。
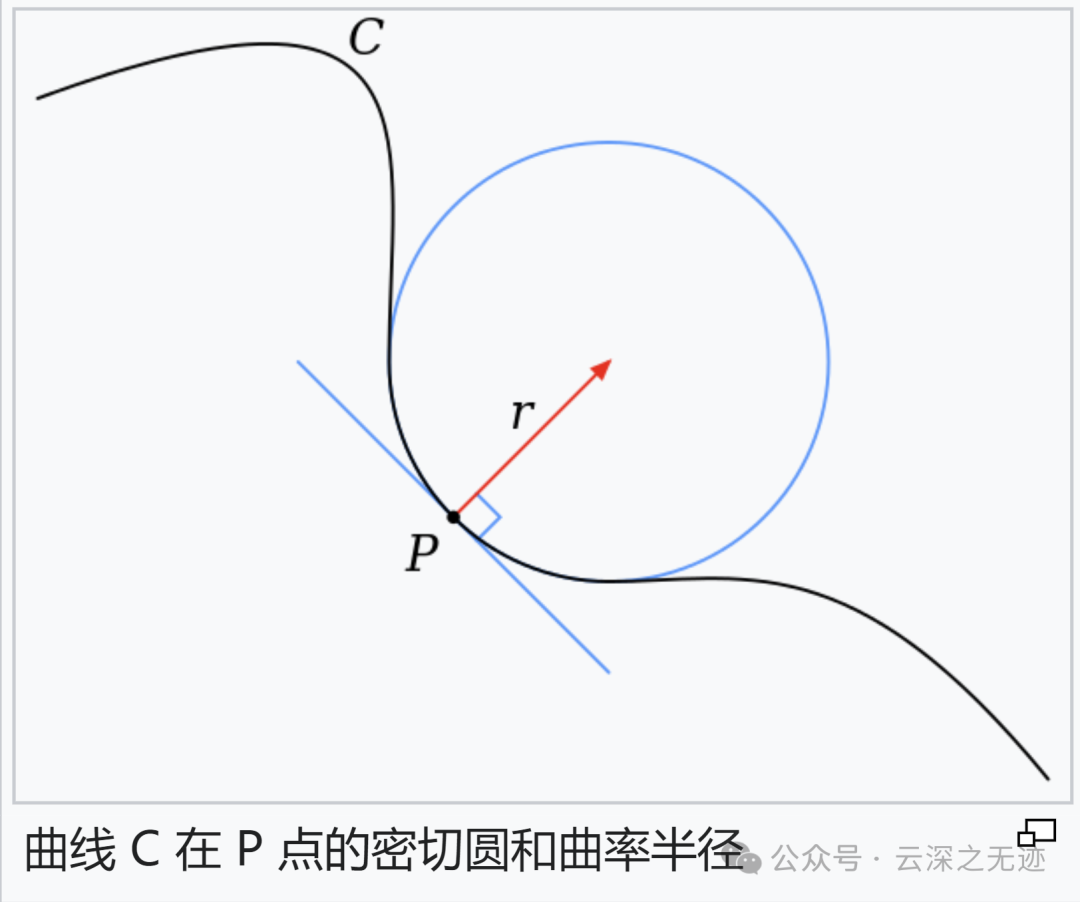

作为补充出现

https://zh.wikipedia.org/zh-cn/%E6%AC%A1%E6%91%86%E7%BA%BFhttps://juejin.cn/post/7316591546992164874https://www.matongxue.com/parts/2018/https://www.matongxue.com/parts/2019/https://www.zhihu.com/question/263774545https://www.elecfans.com/analog/202005151217811.html