奇偶模分析方法一般用于简化对称网络的分析过程。
以对称的双端口网络为例,在大小及相位都相反的奇模信号激励下,因为结构对称,电场的切向分量不存在,穿过该平面的能流也为零,此时其对称面可等效为理想电壁,电壁上任意两点之间的电压差为零,相当于短路。
与之对应在大小及相位都相同的偶模信号激励下,此时对称平面没有电场线及能流穿过,因而电场的法向分量与磁场的切向分量皆不存在,只存在电场的切向分量,对称面可等效为理想磁壁,磁壁上电流为零,相当于开路。
如何由一个对称网络得到奇模电路和偶模电路?
以下面这个耦合线结构为例子:
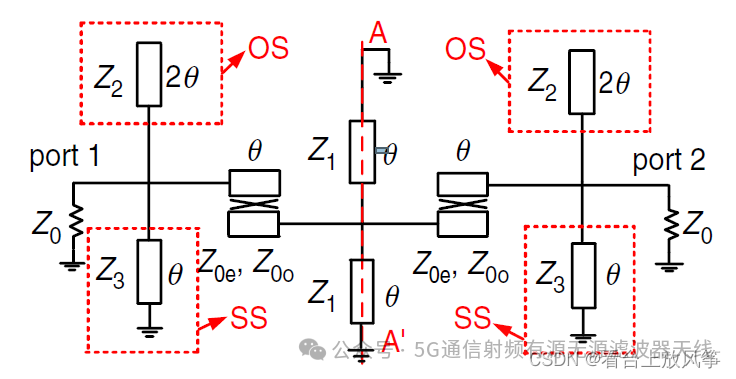
这是一个对称的网络,对称轴为AA’。如果把AA’全部接地 就可以得到奇模电路。如下图所示。
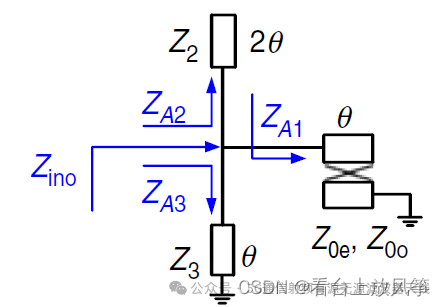
对于偶模电路可以先把对称轴上的两个传输线进行变换: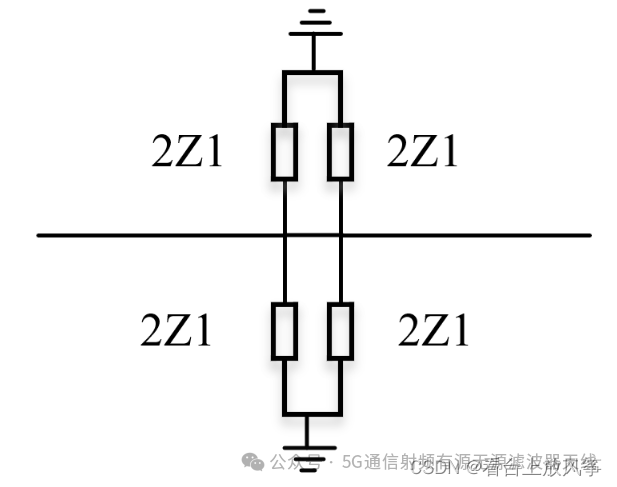
进而可以得到偶摸等效电路
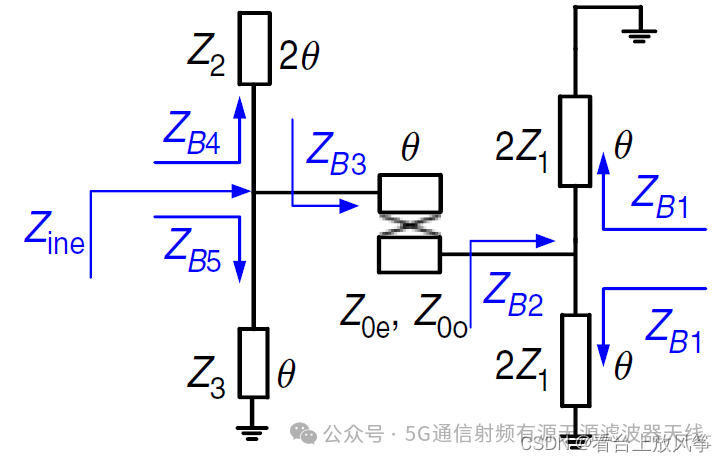
这样分解的目的就是方便求出网络矩阵。
2、典型平行耦合线的阻抗矩阵
a、求特性阻抗为Z0,电长度为θ的均匀传输线段的阻抗矩阵及散射矩阵参量。
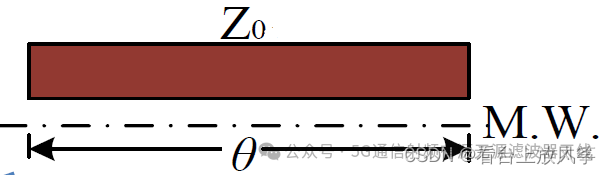
解答:根据奇偶模分析法可以写出奇偶模电路,
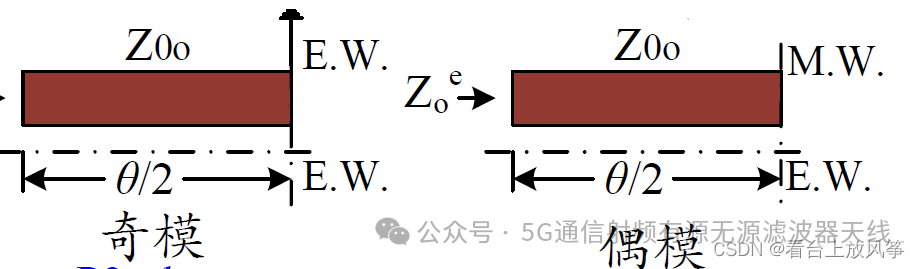
由传输线理论可以知道 开路线的等效阻抗为

短路线的等效阻抗为:
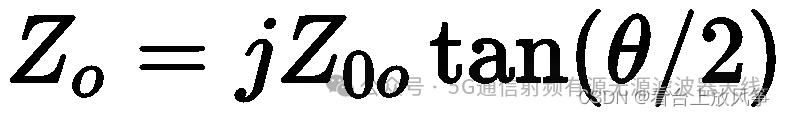
又因为网络矩阵和奇偶模阻抗的关系:

所以可以得到完整的阻抗矩阵分量:
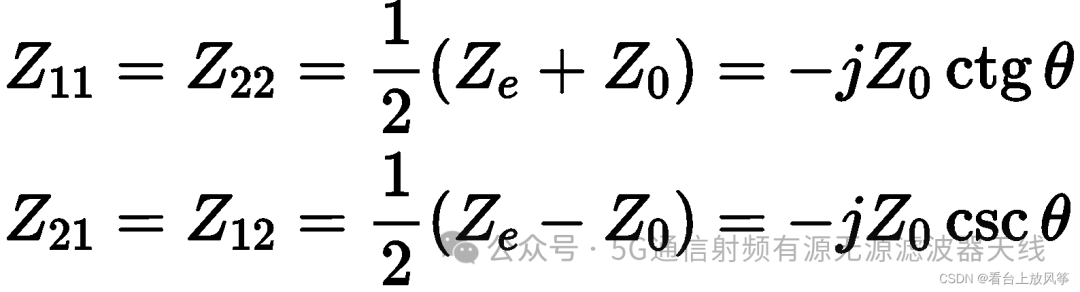
同理 对于开路线和短路线同样也有反射系数公式:
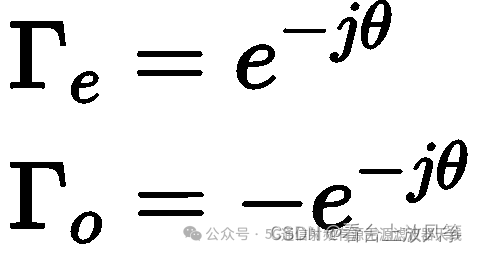
也可以得到散射矩阵:
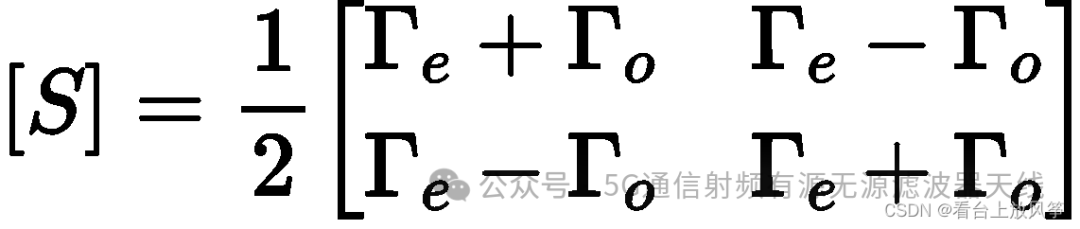
b、 平行耦合线的阻抗矩阵求解
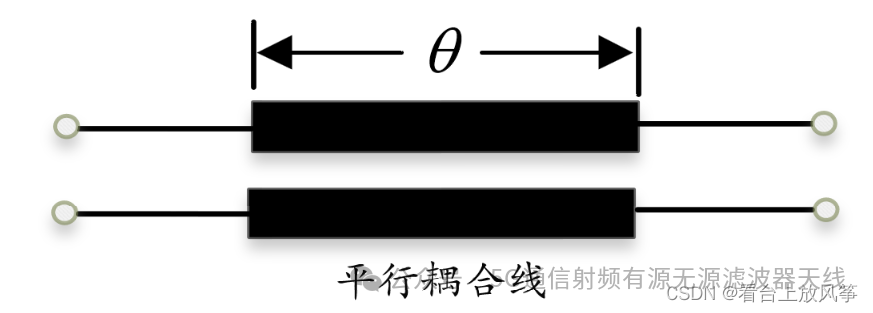
这个也是利用奇偶模分析,先把奇模和偶模写出来,这里可以选择平行传输线为对称轴这样奇模和偶模都是一样就是,如下图。
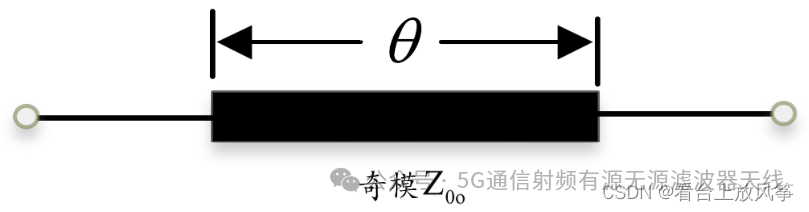
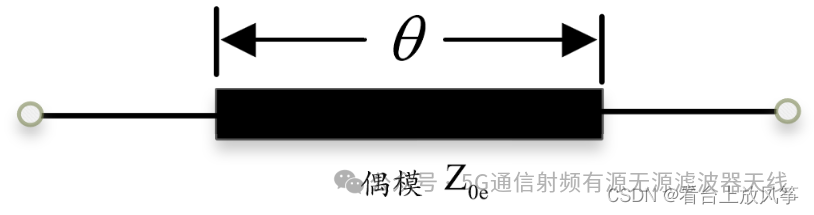
对于这里的偶模和奇模就是上面例题中计算的简单传输线,所以可以直接写出来奇模和偶模的阻抗矩阵。
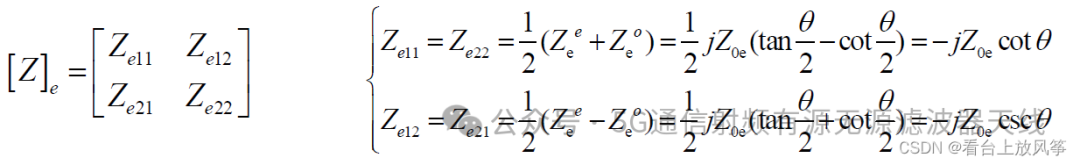
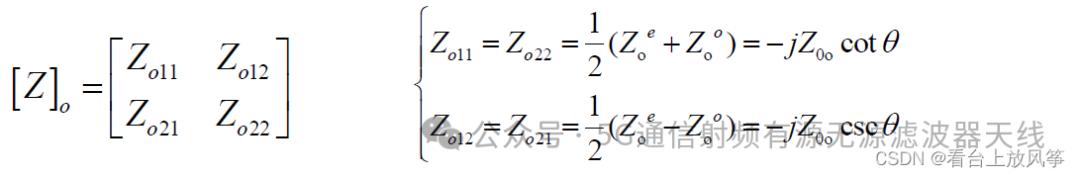
再利用一次原阻抗矩阵矩阵与奇偶模阻抗矩阵的关系,可以得到:

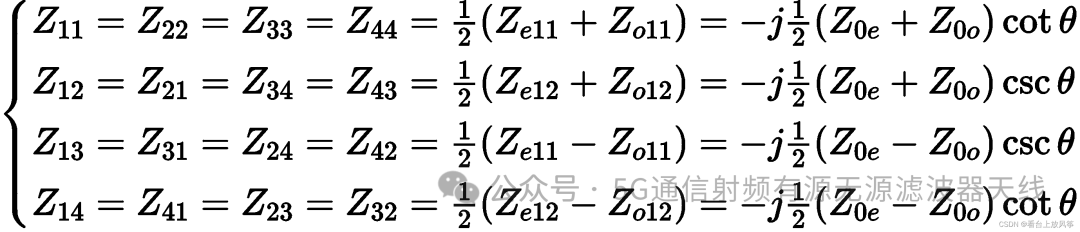
根据阻抗矩阵和导纳矩阵的关系,可以求出导纳的关系式:
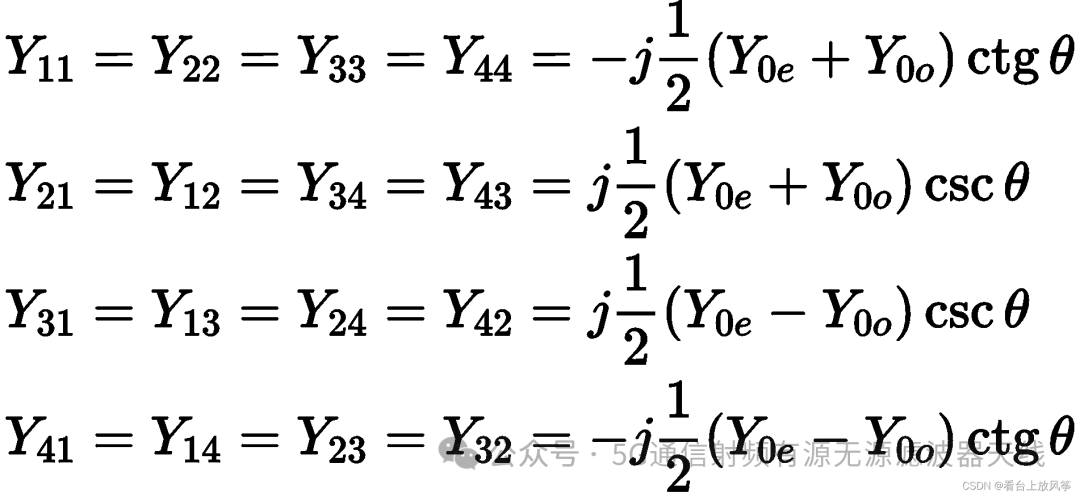
3、任意端接的平行耦合线的输入阻抗
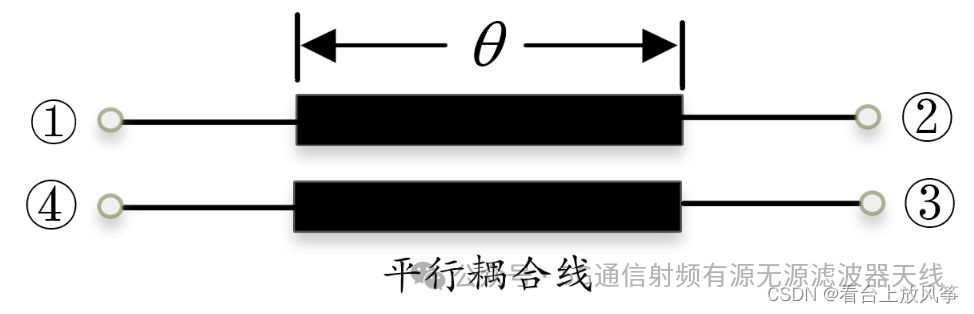
由上图得到的阻抗矩阵,可以得到
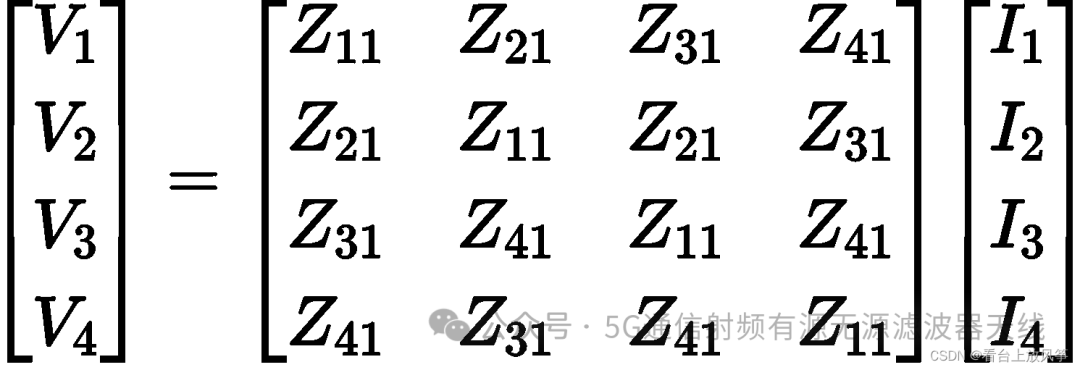
对于四个端口,如果作为输入端、输出端就不改变上面的矩阵。如果对应的端口开路,就把对应位置的电流改成0,如果对应的端口接地,就把对应的端口的电压改成0。
例子:下图中就是二四端口开路的耦合线。
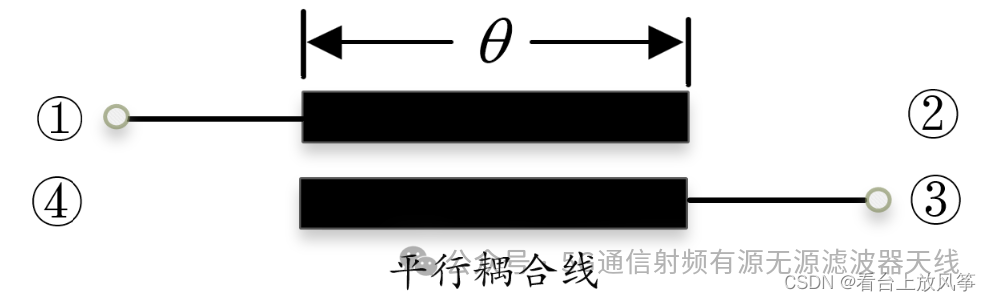
将2、4端口的电流为0,可以写出下面的矩阵:
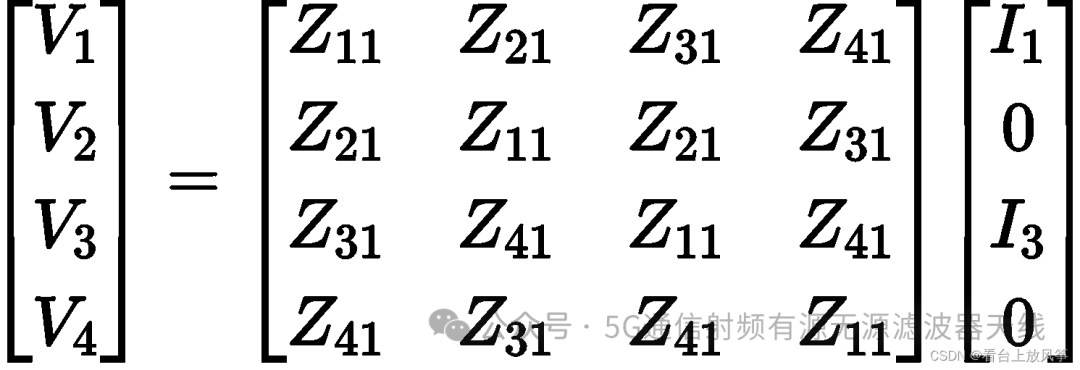
化简上式,可以得到阻抗矩阵。
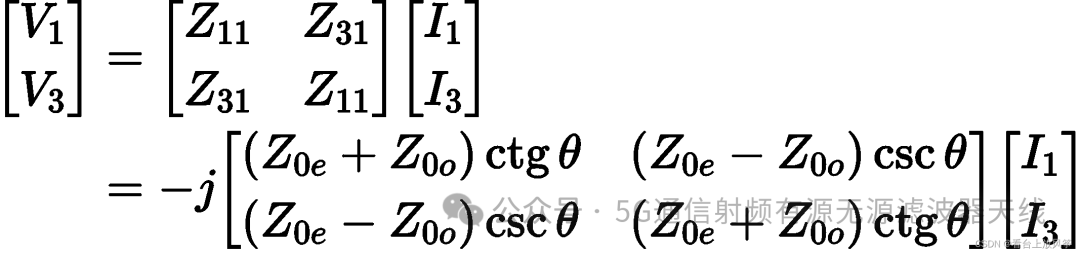
例子: 求解下面的耦合线的输入阻抗:

求解ZA1,仅仅是在上面的例题中把三端口接地,可以得到以下矩阵:
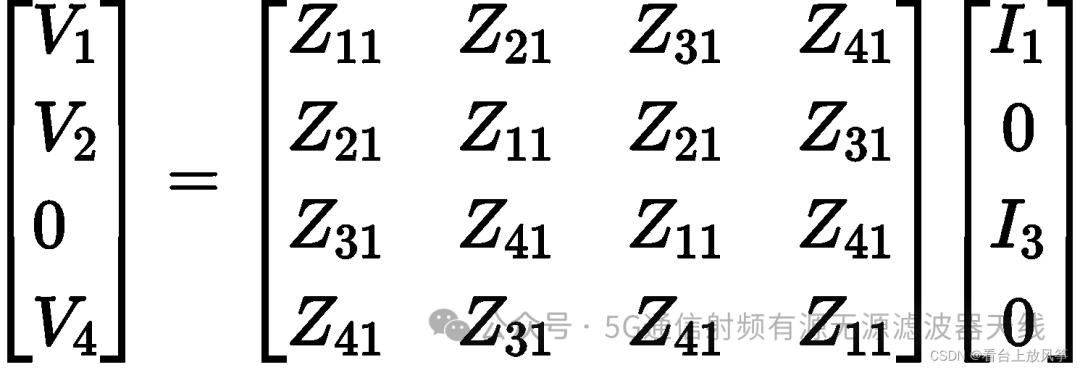
化简可以得到:
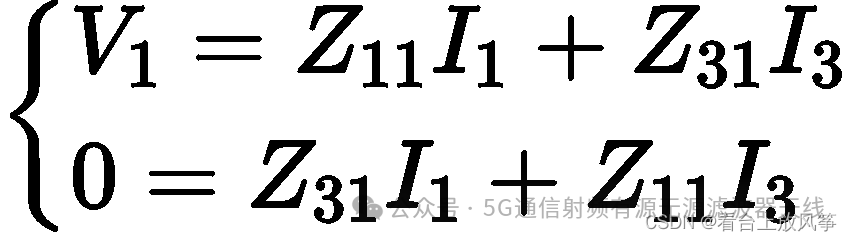
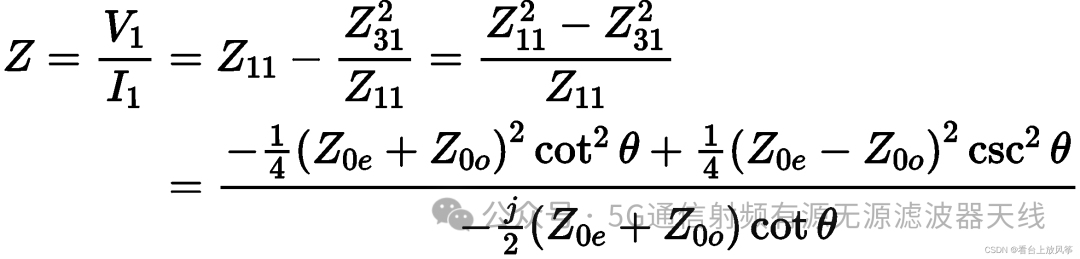
其他的若干形式可以类比写出。
精彩回顾
腔体滤波器技术提升解决方案
一座5G基站它的成本是由哪些部分组成?
腔体滤波器设计之----自动单腔频率温飘
秒仿糖葫芦串形低通
秒仿糖葫芦型低通后续之----低通优化
[超级全]一百多页的射频基础知识资料,看这一篇就够了
TE01模介质滤波器滤波器
无源互调浅析
如何选择谐振杆的尺寸使功率容量达到最佳
金属介质混合+零腔案例
三模并联耦合介质波导滤波器仿真实例
同轴高低阻抗型低通的公差影响几何?
Coupfil对高阶强零点生成的结果偶会出错
陶瓷滤波器的各项制备工序讲解_简介篇
(干货)陶瓷滤波器讲解----材料篇
(干货)陶瓷滤波器讲解----材料制备篇
[东南大学射频讲义]射频与微波基础知识
陶瓷滤波器讲解----陶瓷材料检测篇
BAW,SAW和FBAR滤波器剖析
比较全的射频基础知识讲座
射频连接器只看这一篇就够了!设计、查阅、收藏宝典!
LTCC、IPD、SAW、BAW、FBAR滤波器入门以及应用场景分析
欢迎加入滤波器、功放、射频收发信、基站、天线、环形隔离器、功分耦合、连接器、线缆负载等射频微波大家庭
点击上侧公众号可关注后加群
本团队提供可信可靠的射频功放有源无源相关产品各种定制化服务,响应快、专业强、质量可信,敬请咨询,电话微信同号18665903037
点"在看"为本文点个赞,才算看完呦