
信号与系统 2023(春季) 作业要求 - 第六次作业[1]
信号与系统 2023(春季) 作业参考答案 - 第六次作业[2]
(1)
已知信号的波形如下图所示,是正弦信号的绝对值在 之间的波形。根据傅里叶变换公式求解该信号的频谱,并绘制该信号的幅度谱。
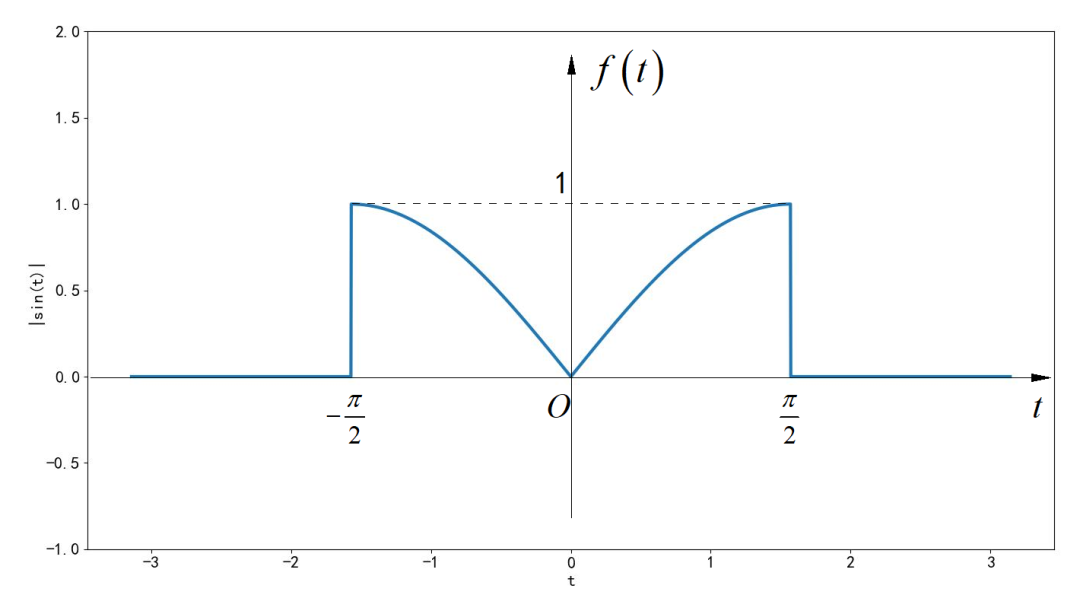
▲ 图1.1.1 信号的波形对于该信号的频谱计算,可以直接利用公’式进行。其中建议大家对于被积分sin函数利用Euler公式更换成两个共轭复指数叠加的形式,然后在进行求解,这样便于写出积分的原函数。
根据傅里叶变换公式求解下面函数表达式对应信号的频谱。
(2)

(3)

(4)

(1)
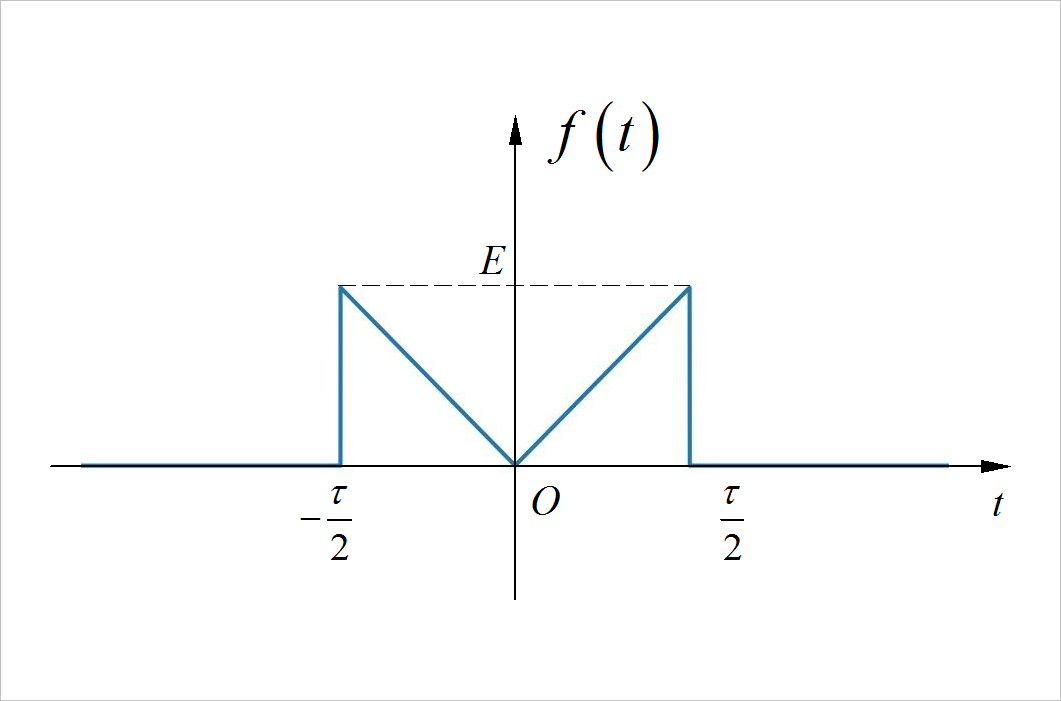
▲ 图1.1.3 信号的波形提示:将信号看成矩形信号 与等腰三角形信号的差值。然后借助于矩形信号与等腰三角形信号的傅里叶变换结果写出该信号的频谱。
(2)
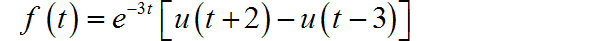
(1)
直接根据傅里叶反变换公式,将下面信号的频谱进行反变换,获得信号时域波形。
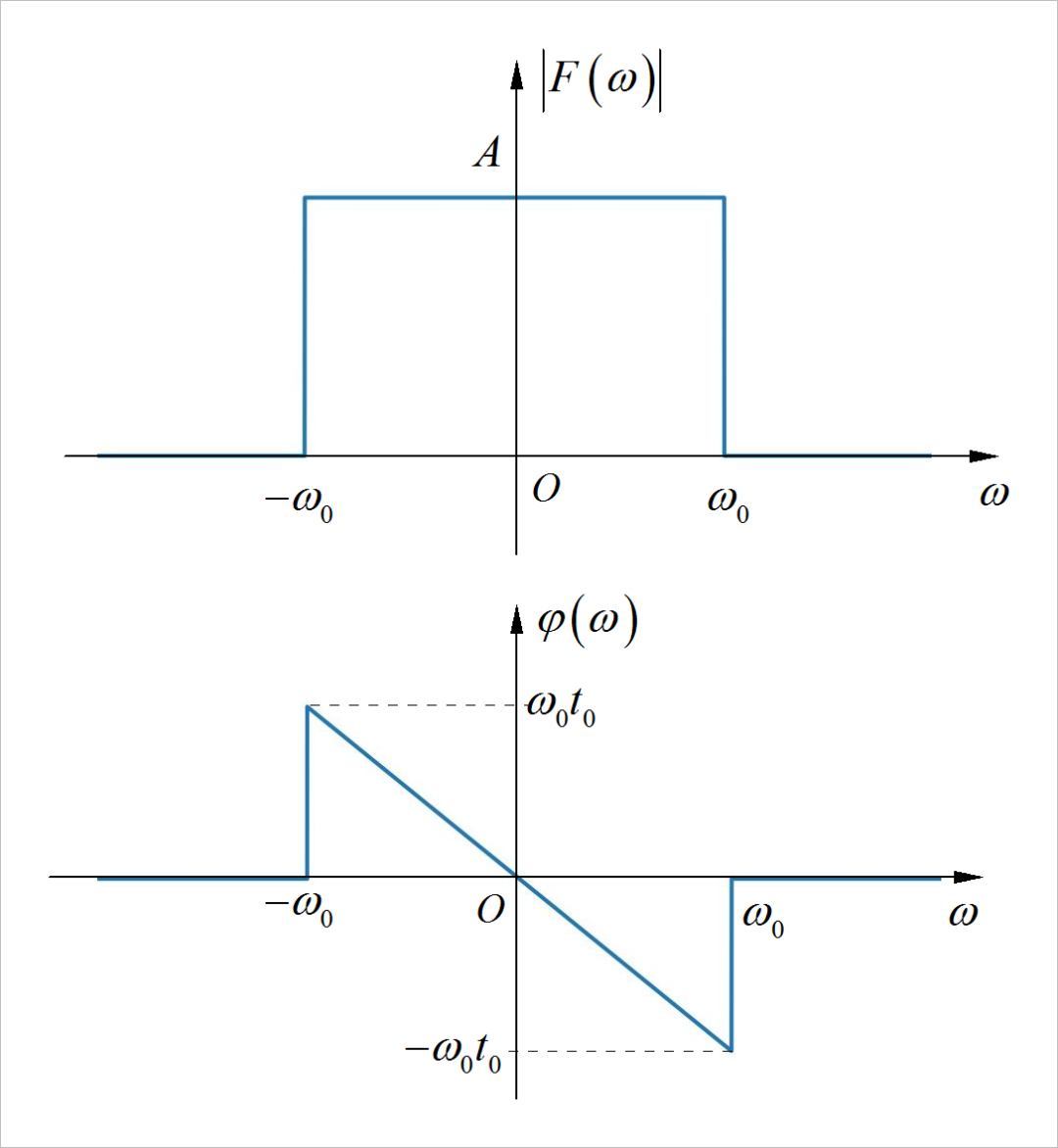
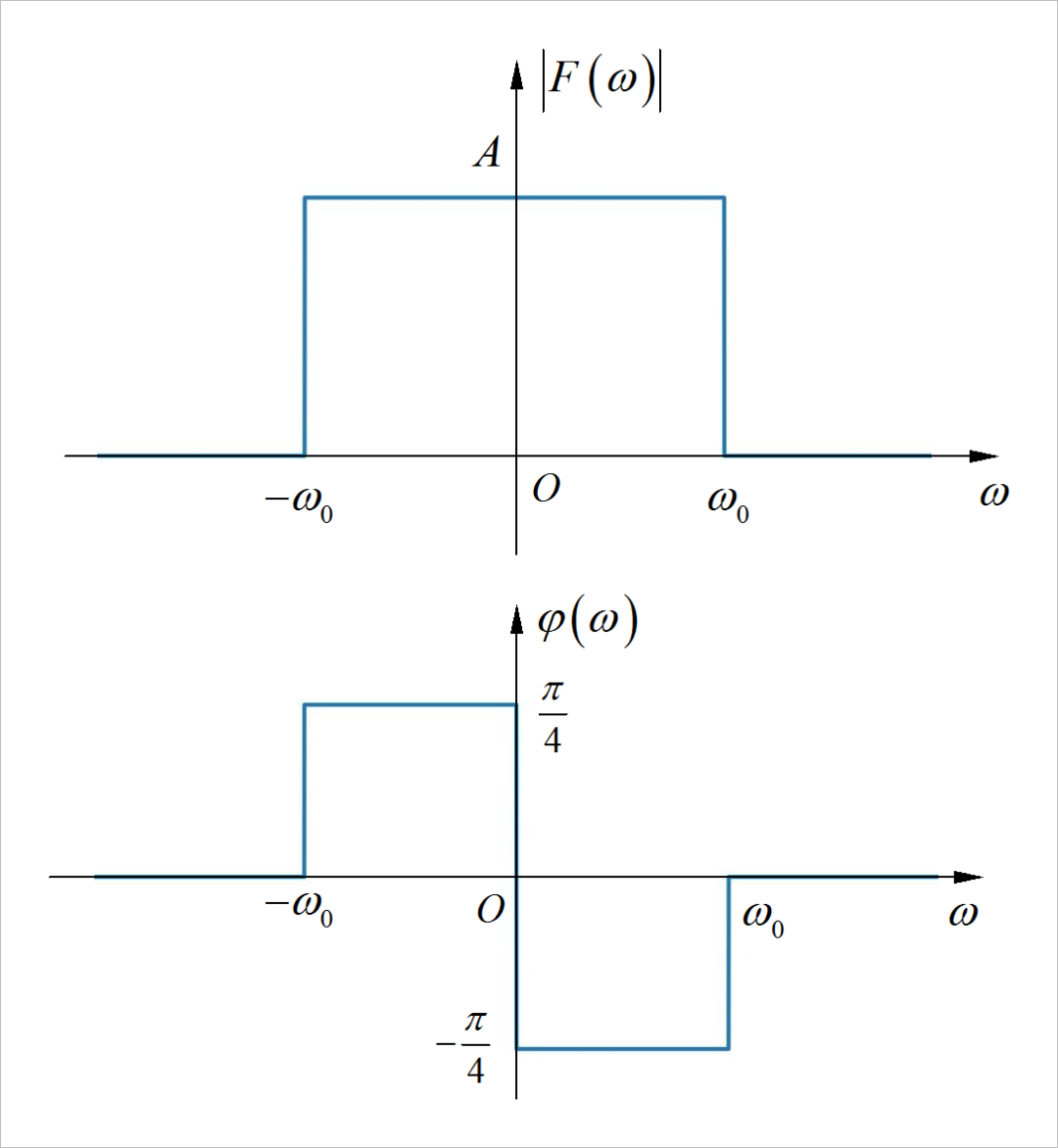
▲ 图1.2.2 信号的幅度谱和相位谱 (2)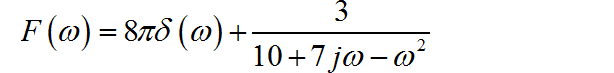
提示:对于 进行因式分解,然后在分别写出对应的时域信号。
直接根据傅里叶反变换公式,将下面信号的频谱进行反变换,获得信号表达式 。
(1)
▲ 图1.2.1 信号的幅度谱和相位谱(2)
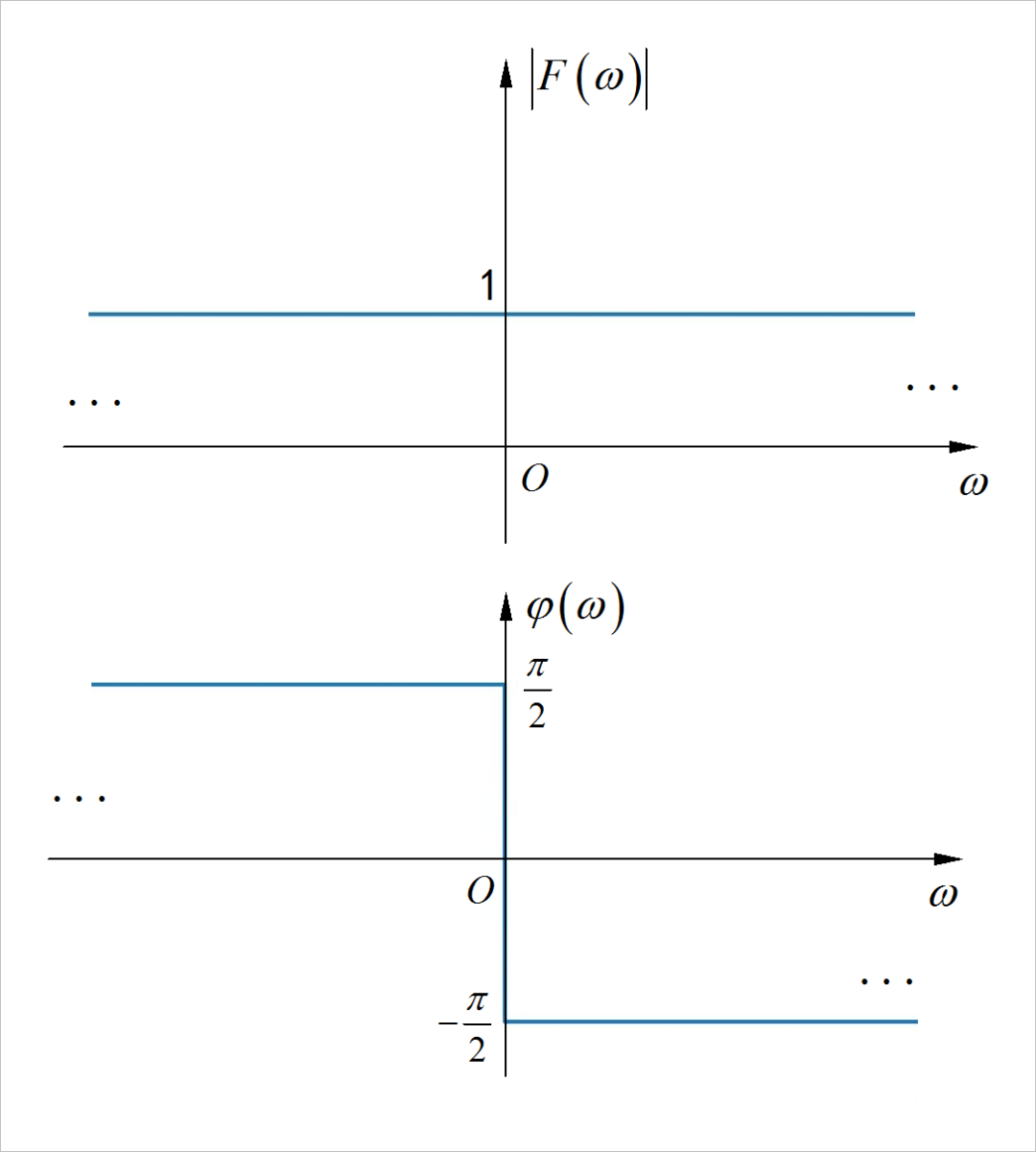
▲ 图1.2.3 信号的幅度谱和相位谱注:上面幅频、相频函数都是往两边无穷延伸的。
根据 表达式,按照傅里叶变换的对偶特性求解 。
已知信号 的波形如下图所示:
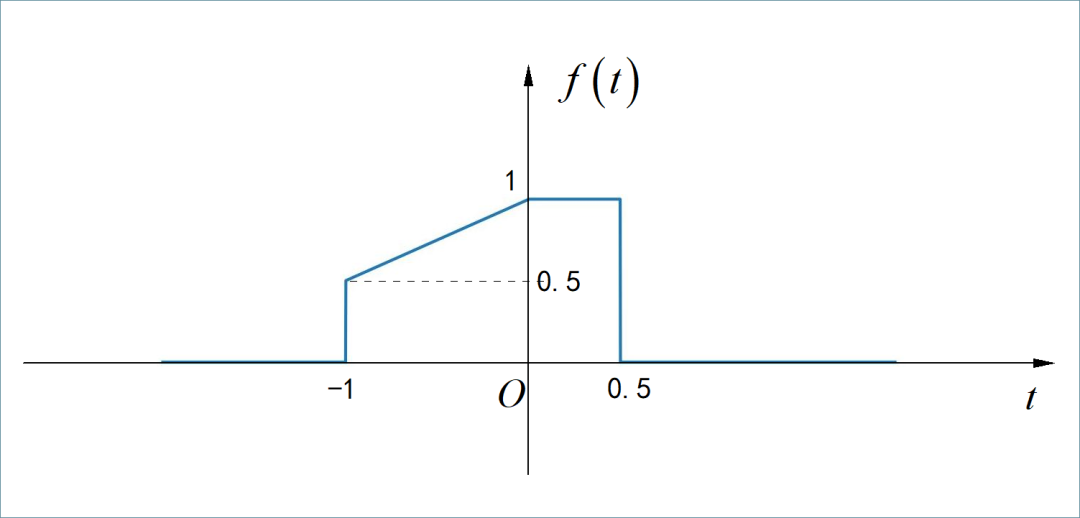
▲ 图1.3.1 信号的波形假设它的傅里叶变换为:
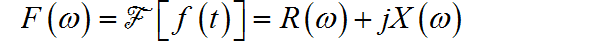
请在不具体求出 的表达式的情况下,求解:
(1) 求下面积分数值:

(2) 求 傅里叶反变换的信号波形;
(3) 求 的取值。
提示:这个信号是 第二次作业[4] 中进行奇偶分解习题中的信号波形。
在MATLAB 中使用 fourier,ifourer命令可以求取函数的傅里叶变换数学表达式。请在MATLAB中使用相关命令求取下面信号的傅里叶变换和傅里叶逆变换。



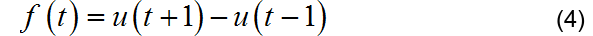
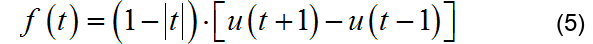
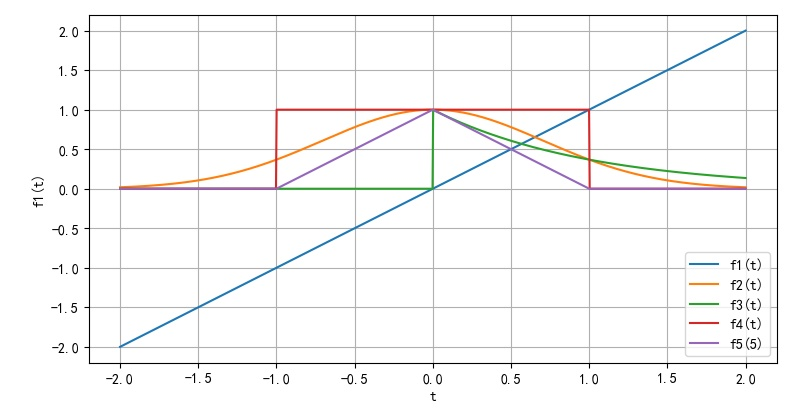
▲ 信号的波形from headm import *
t = linspace(-2, 2, 1000)
plt.plot(t, t, label='f1(t)')
plt.plot(t, exp(-t**2), label='f2(t)')
plt.plot(t, exp(-t)*heaviside(t, 0.5), label='f3(t)')
plt.plot(t, heaviside(t+1,0.5)-heaviside(t-1,0.5), label='f4(t)')
plt.plot(t, (1-abs(t))*(heaviside(t+1, 0.5)-heaviside(t-1, 0.5)), label='f5(5)')
plt.xlabel("t")
plt.ylabel("f1(t)")
plt.grid(True)
plt.tight_layout()
plt.legend(loc='lower right')
plt.show()
fourier((heaviside(t+1)-heaviside(t-1))*(1-abs(t)))'
fourier(heaviside(t+1)-heaviside(t-1))'
fourier(1/t)'
fourier(exp(-t^2))'
fourier(exp(-t)*heaviside(t))'
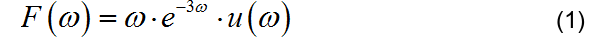


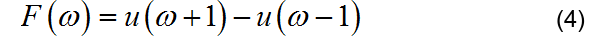
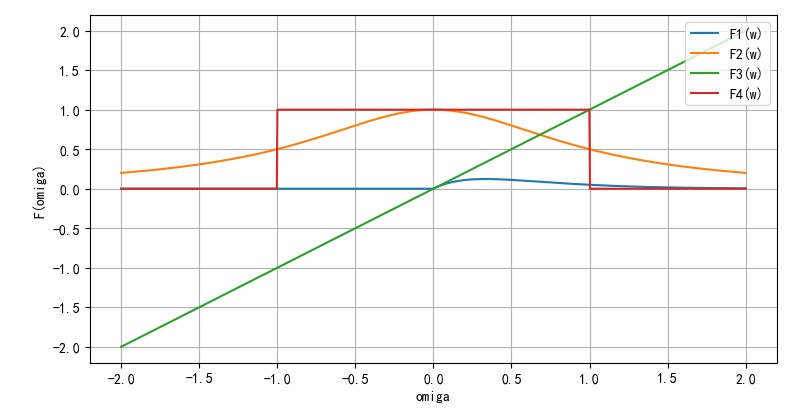
▲ 图2.1.2 频谱信号波形from headm import *
w = linspace(-2, 2, 1000)
plt.plot(w, w*exp(-3*w)*heaviside(w, 0.5), label='F1(w)')
plt.plot(w, 1/(1+w**2), label='F2(w)')
plt.plot(w, w, label='F3(w)')
plt.plot(w, heaviside(w+1, 0.5)-heaviside(w-1,0.5), label='F4(w)')
plt.xlabel("omiga")
plt.ylabel("F(omiga)")
plt.grid(True)
plt.legend(loc="upper right")
plt.tight_layout()
plt.show()
ifourier(w*exp(-3*w)*heaviside(w))'+1
ifourier(1/(1+w^2))
ifourier(w)
ifourier(heaviside(w+1)-heaviside(w-1))
普通的实数信号 经过傅里叶变换之后,会产生一个复数频谱 。根据实际需要,我们可以从复频谱中的实部、虚部、幅值、相角获得我们需要的信息。
根据傅里叶变换的“奇偶虚实”特性,我们知道:
那么信号频谱的幅值,相角又反映了信号的什么信息?
下面通过实验来让我们从 一个角度看看信号频谱的幅值、相角内包含的信息。
实验灰度图像数据可以直接从本网页,鼠标右键点击“图片零存为” 获得。

▲ 图2.2.1 测试图片利用二维快速傅里叶变换,获得上灰度图像的频谱。下给出了上述图片的幅度和相位谱。
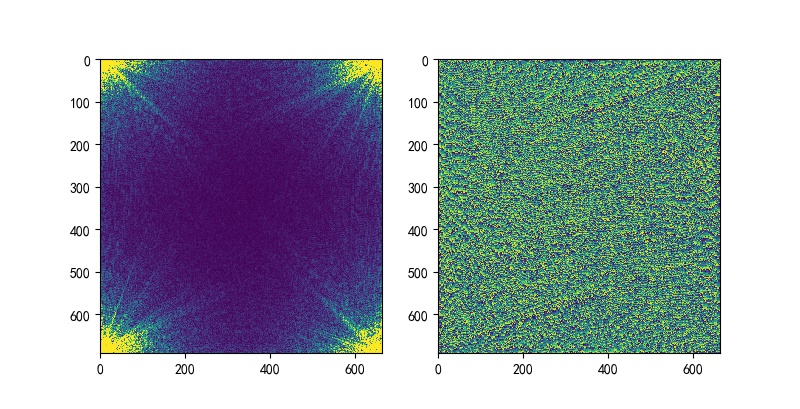
▲ 图像的幅度和相位谱import sys,os,math,time
import matplotlib.pyplot as plt
from numpy import *
import cv2
imageid = 3
filename = tspgetdopfile(imageid)
print(filename)
img = cv2.imread(filename)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
imgfft = numpy.fft.fft2(gray)
print(shape(imgfft))
imgabs = abs(imgfft)
imgabs[imgabs > 20000] = 20000
imgangle = angle(imgfft)
plt.subplot(1,2,1)
plt.imshow(imgabs)
plt.subplot(1,2,2)
plt.imshow(imgangle)
plt.show()
print('\a')
将计算结果中的相位都置为0,进行傅里叶反变换,获得图片频谱中幅度图像信息。
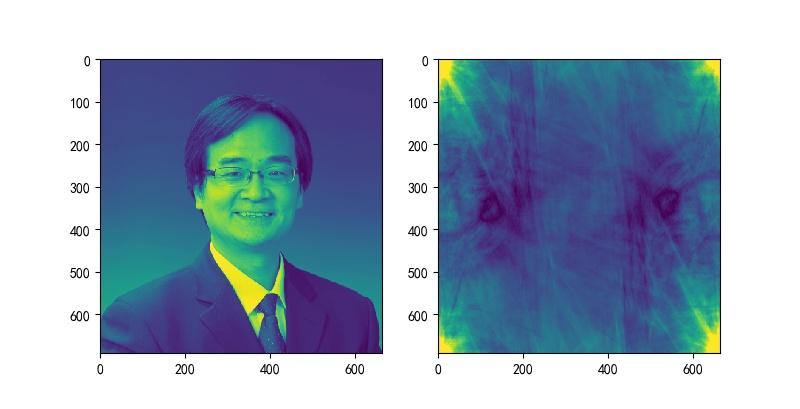
▲ 图2.2.3 原图像以及幅度谱恢复的图像信息img0 = numpy.fft.ifft2(imgfft)
img1 = numpy.fft.ifft2(abs(imgfft))
img1[img1>255]=255
plt.subplot(1,2,1)
plt.imshow(abs(img0))
plt.subplot(1,2,2)
plt.imshow(abs(img1))
plt.show()
注意:请注意上述代码中,对于数组img1进行饱和处理的作用。
将计算结果中的幅值都置为1,进行傅里叶反变换,获得图片频谱中的相位图像信息。
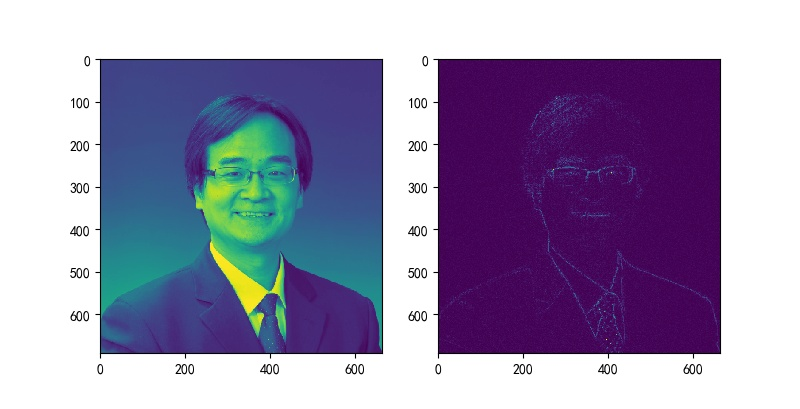
▲ 原始图像以及相位恢复的图像信息img0 = numpy.fft.ifft2(imgfft)
img1 = numpy.fft.ifft2(imgfft/abs(imgfft))
plt.subplot(1,2,1)
plt.imshow(abs(img0))
plt.subplot(1,2,2)
plt.imshow(abs(img1))
plt.show()
通过对比从图像频谱中的幅度和相位恢复结果来看,讨论图像中的结构信息主要是分布在幅度谱还是相位谱?
对于声音信号进行相同的分析,分别从声音信号中的幅度谱和相位谱还原对应的声音,讨论一下从哪一部分可以听出原来的声音信号。
下面我利用 Audacity音频录制软件[5] 截取了 西瓜视频中降央卓玛经典歌曲《西海情歌[6] 中的片段(时长1:15),转存成 .WAV文件。

▲ 图2.2.5 西海情歌这个数据文件也可以从下面链接下载:
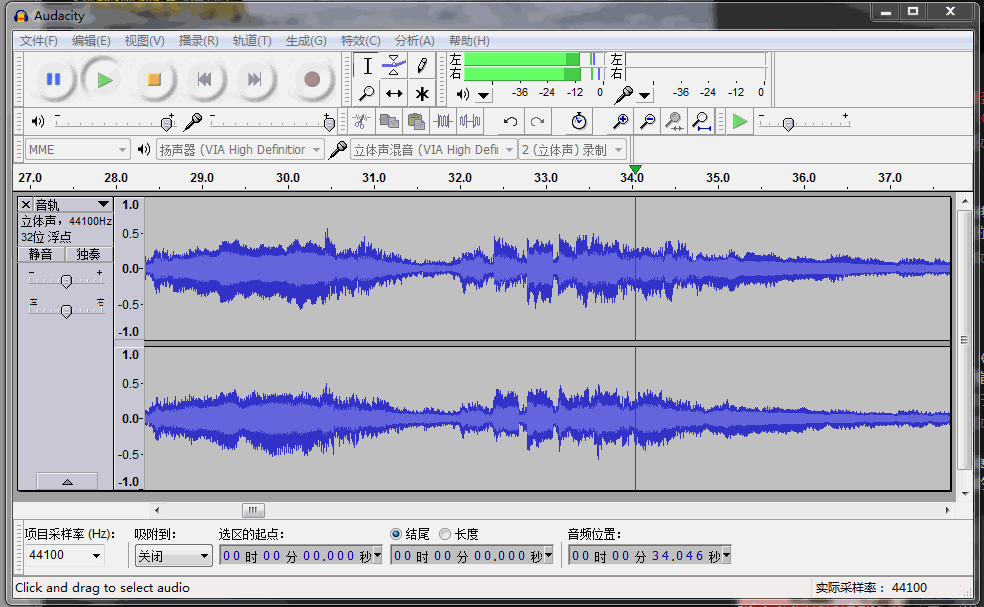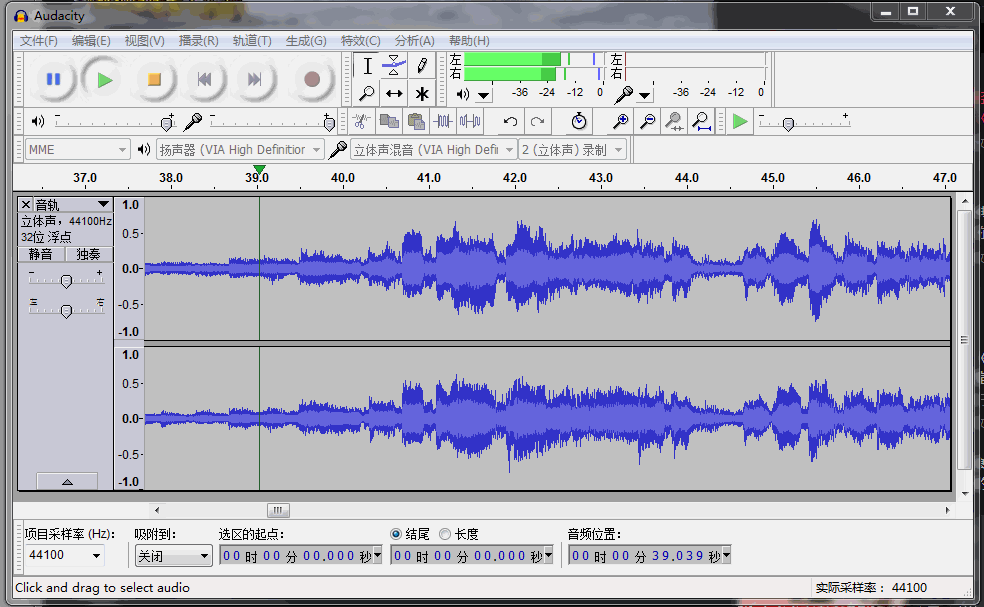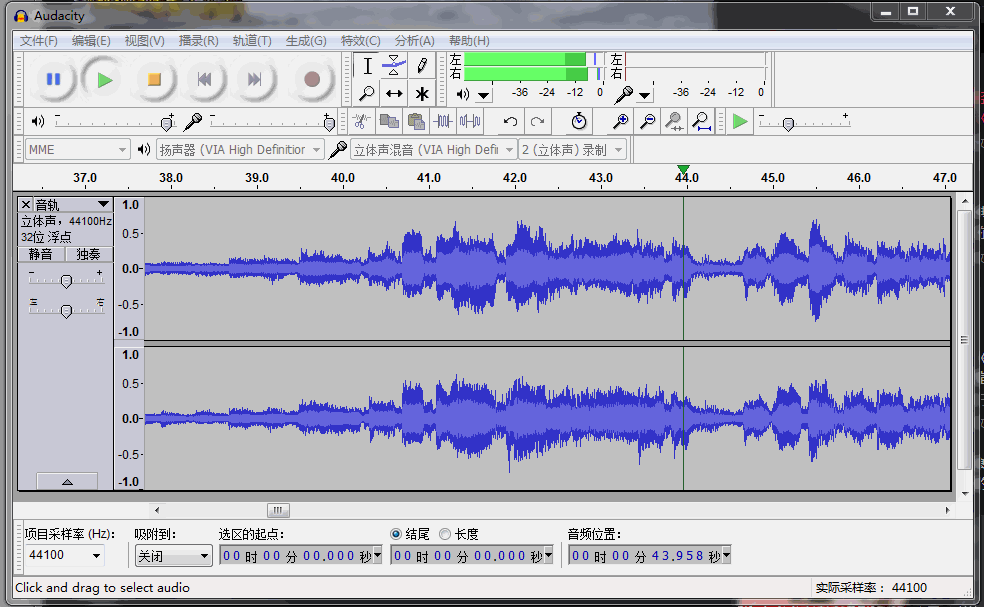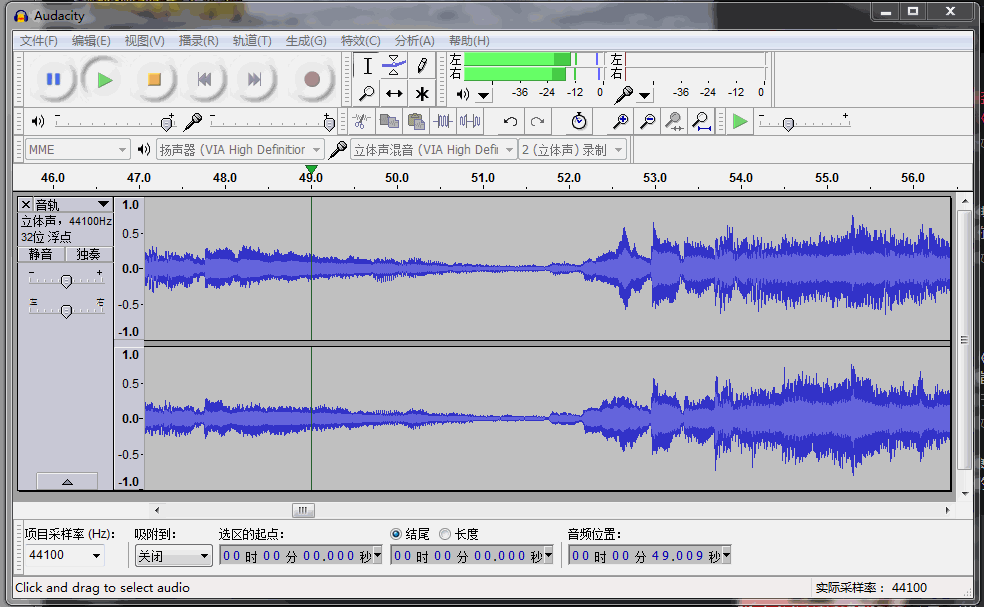
▲ 图2.2.6 截取音频信号参考博文 电话双音频拨号声音中的干扰信号[8] 中对于音频WAV文件的读写方法,将上述波形文件进行读取。
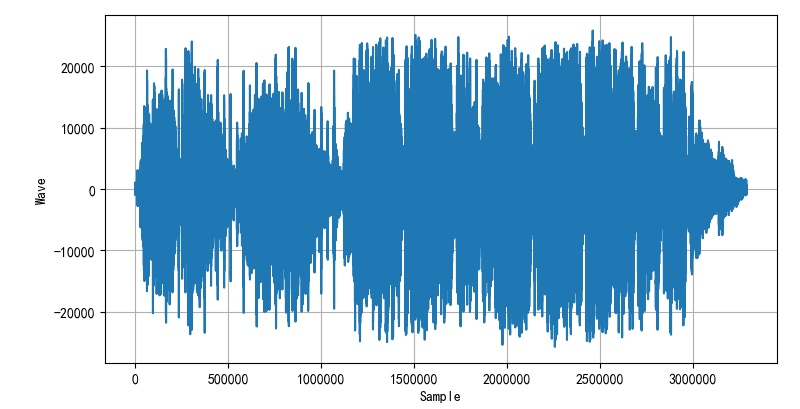
▲ 音乐片段波形filename = r'D:\Temp\XIHaiLoveSong.wav'
from scipy.io import wavfile
sample_rate,sig = wavfile.read(filename)
printf(sample_rate, shape(sig))
plt.plot(sig)
plt.xlabel("Sample")
plt.ylabel("Wave")
plt.grid(True)
plt.tight_layout()
plt.show()
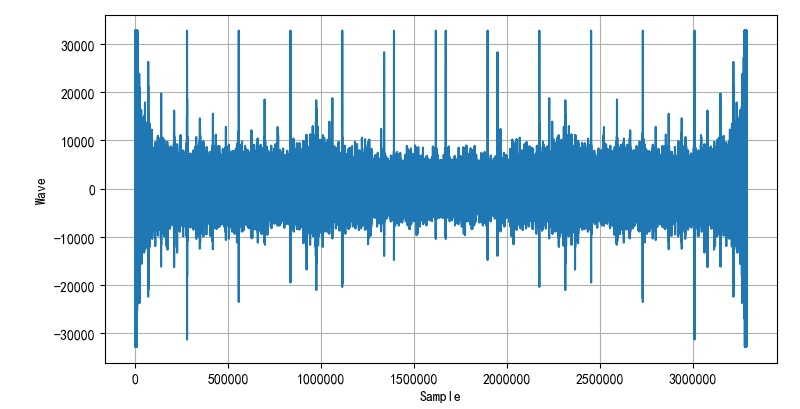
▲ 幅度品返回的波形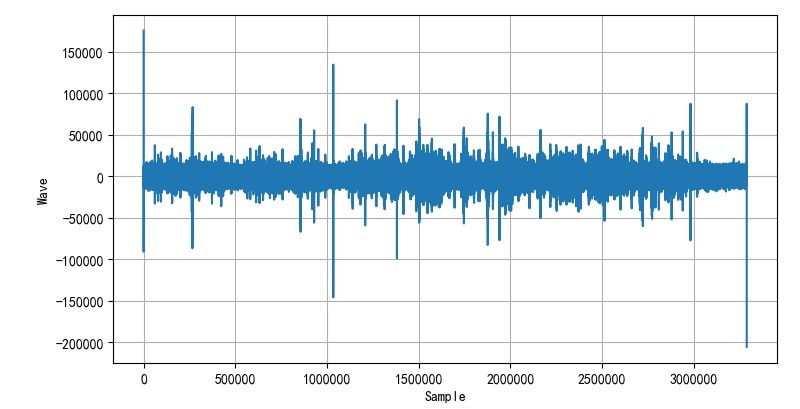
▲ 相位谱恢复的信息from headm import *
filename = r'D:\Temp\XIHaiLoveSong.wav'
from scipy.io import wavfile
sample_rate,sig = wavfile.read(filename)
sigfft = numpy.fft.fft(sig)
siga = numpy.fft.ifft(sigfft/abs(sigfft)*1e7)
#siga[siga>=0x7fff]=0x7fff
#siga[siga<-0x7fff]=-0x7fff
outfile1 = r'd:\temp\1.wav'
wavfile.write(outfile1, sample_rate, siga.astype(int16))
plt.plot(siga.real)
plt.xlabel("Sample")
plt.ylabel("Wave")
plt.grid(True)
plt.tight_layout()
plt.show()
大家可以通过试听恢复的声音信号,看幅度谱中和相位谱恢复的音频中哪一个还可以听出原来的歌曲。
信号与系统 2023(春季) 作业要求 - 第六次作业: https://zhuoqing.blog.csdn.net/article/details/129854671
[2]信号与系统 2023(春季) 作业参考答案 - 第六次作业: https://zhuoqing.blog.csdn.net/article/details/129940958
[3]作业辅导视频 SS2023-HW6:傅里叶变换公式求解: https://zhuoqing.blog.csdn.net/article/details/129997987
[4]第二次作业: https://zhuoqing.blog.csdn.net/article/details/129301254
[5]Audacity音频录制软件: https://www.audacityteam.org/
[6]西瓜视频中降央卓玛经典歌曲《西海情歌: https://www.ixigua.com/7008037669968019976?id=7079714658432745995&logTag=be03debc0c4bc554289e
[7]西海情歌片段:: https://gitee.com/tsinghuajoking/teaching-resources/blob/master/Signals&Systems/2022%E5%B9%B4/XIHaiLoveSong.wav
[8]电话双音频拨号声音中的干扰信号: https://blog.csdn.net/zhuoqingjoking97298/article/details/122451410