15bit电阻DAC输出公式

原创 TsinghuaJoking 2024-04-05 08:27 633浏览 0评论 0点赞

汽车照明的秘密武器，竟然是…… 从清华教授到企业高管，这场大会把 MATLAB/Simulink 前沿应用讲透了

一、前言

今天上午对 8比特电阻DAC输出公式进行了推导，由此计算出单片机 IO 口内阻对 DAC线性精度的影响。现在正好还有点时间，就耐下心来，最终求出 15比特 DAC 输出电压的解析公式，验证单片机IO内阻对于DAC的影响是否和通道数有关系。

二、推导过程

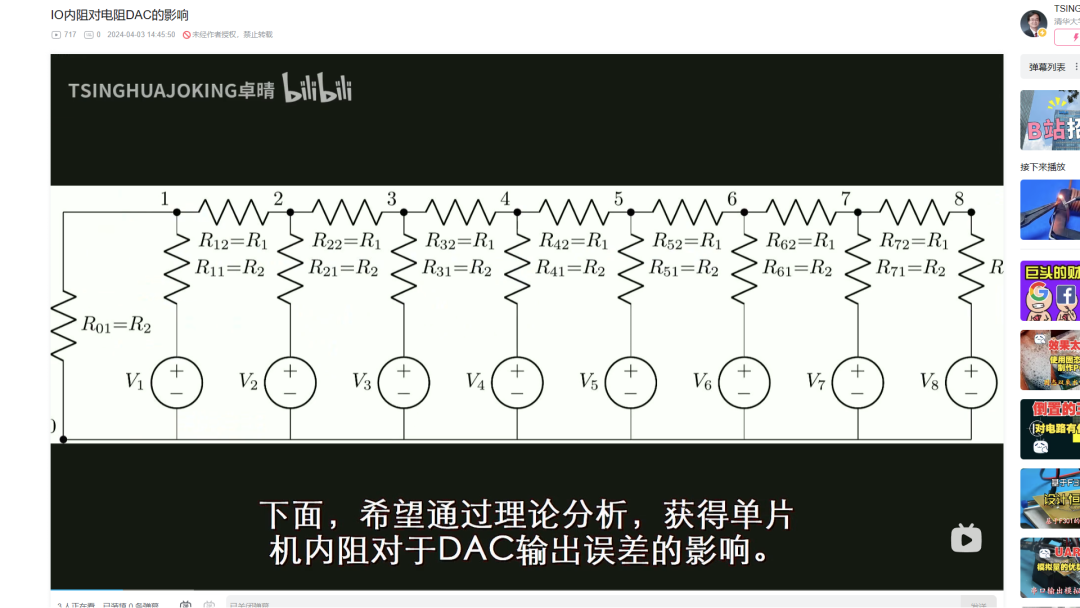
生成DAC理论公式还是使用上午的 LCA 软件包，只是将器电路结构增加到 15个通道。这是LCA 绘制的R2R 电阻DAC的电路图。之后，它生成了最后电路的输出的解析表达式。这个求解过程计算机消耗了 10分钟左右。

#!/usr/local/bin/python
# -*- coding: gbk -*-
#******************************
# TEST1.PY                   - by Dr. ZhuoQing 2024-04-03
#
# Note:
#******************************

from headm import *
from sympy                  import symbols,simplify,expand,print_latex
from sympy                  import *
from lcapy                  import *
from sympy                  import symbols,simplify,expand,print_latex
from sympy                  import *

#------------------------------------------------------------

cct = Circuit("""

V1   1_0 0_1 dc V1  ; down
W0   0  0_1         ; right
R01  0  0_0   R2    ; up
R11  1_0 1    R2    ; up
W00  1  0_0         ; left

R12  1 2      R1    ; right
W1   0_1 0_2        ; right
V2   2_0 0_2 dc V2  ; down
R21  2_0 2    R2    ; up

R22  2 3      R1    ; right
W2   0_2 0_3        ; right
V3   3_0 0_3 dc V3  ; down
R31  3_0 3    R2    ; up

R32  3 4      R1    ; right
W3   0_3 0_4        ; right
V4   4_0 0_4 dc V4  ; down
R41  4_0 4    R2    ; up

R42  4 5      R1    ; right
W4   0_4 0_5        ; right
V5   5_0 0_5 dc V5  ; down
R51  5_0 5    R2    ; up

R52  5 6      R1    ; right
W5   0_5 0_6        ; right
V6   6_0 0_6 dc V6  ; down
R61  6_0 6    R2    ; up

R62  6 7      R1    ; right
W6   0_6 0_7        ; right
V7   7_0 0_7 dc V7  ; down
R71  7_0 7    R2    ; up

R72  7 8      R1    ; right
W7   0_7 0_8        ; right
V8   8_0 0_8 dc V8  ; down
R81  8_0 8    R2    ; up

R82  8 9      R1    ; right
W8   0_8 0_9        ; right
V9   9_0 0_9 dc V9  ; down
R91  9_0 9    R2    ; up

R92  9 10     R1    ; right
W9   0_9 0_10        ; right
V10  10_0 0_10 dc V10 ; down
R101 10_0 10    R2    ; up

R102 10 11     R1    ; right
W10  0_10 0_11      ; right
V11  11_0 0_11 dc V11 ; down
R111 11_0 11    R2    ; up

R112 11 12     R1    ; right
W11  0_11 0_12      ; right
V12  12_0 0_12 dc V12 ; down
R121 12_0 12    R2    ; up

R122 12 13     R1    ; right
W12  0_12 0_13      ; right
V13  13_0 0_13 dc V13 ; down
R131 13_0 13    R2    ; up

R132 13 14     R1    ; right
W13  0_13 0_14      ; right
V14  14_0 0_14 dc V14 ; down
R141 14_0 14    R2    ; up

R142 14 15     R1    ; right
W14  0_14 0_15      ; right
V15  15_0 0_15 dc V15 ; down
R151 15_0 15    R2    ; up


""")


#------------------------------------------------------------
import pyautogui

schfn = r'd:\temp\cct.png'
cct.draw(schfn)

rect = tspgetwindowrect(schfn.split('\\')[-1])
pyautogui.FAILSAFE = False
if sum(rect) != 0:
    pyautogui.click(rect[2]-30, rect[1]+15)
os.startfile(schfn)
printf('\a')
tspfocuswindow("TEASOFT:3")

#------------------------------------------------------------


result = cct[15].V(t)

printf(result)

exit()

#------------------------------------------------------------
mstr = latex(result)
printf(mstr)
_=tspexecutepythoncmd("msg2latex")

#------------------------------------------------------------
#        END OF FILE : TEST1.PY
#******************************

▲ 图1.2.1 15bitDAC结构

将 LCA推导出输出电压的公式，转换成了 Python 程序。这样可以计算出在不同的 DAC 数值情况下，电阻网络的输出。可以看到，在 R1,R2分别为 10k，20k欧姆的情况下，输出电压与DAC 数值之间呈现严格的线性关系。这是输出电压与DAC理论值之间的误差，除了因为计算机浮点精度所引起的微小误差之外，公式搜得到的数值与理论值是相同的。

#!/usr/local/bin/python
# -*- coding: gbk -*-
#******************************
# TEST3.PY                   - by Dr. ZhuoQing 2024-04-03
#
# Note:
#******************************

from headm import *

def Dr1r2(R1,R2):
    return 2*R1**14 + 55*R1**13*R2 + 676*R1**12*R2**2 + 4900*R1**11*R2**3 + 23276*R1**10*R2**4 +\
           76153*R1**9*R2**5 + 175560*R1**8*R2**6 + 286824*R1**7*R2**7 + 329460*R1**6*R2**8 +\
           260338*R1**5*R2**9 + 136136*R1**4*R2**10 + 44200*R1**3*R2**11 + 8008*R1**2*R2**12 + 665*R1*R2**13 + 16*R2**14

def N1(R1,R2):
    return R2**14


def N10(R1,R2):
    return (2*R1**9*R2**5 + 33*R1**8*R2**6 + 225*R1**7*R2**7 + 819*R1**6*R2**8 + 1716*R1**5*R2**9 +
            2079*R1**4*R2**10 + 1386*R1**3*R2**11 + 450*R1**2*R2**12 + 54*R1*R2**13 + R2**14)


def N11(R1,R2):
    return (2*R1**10*R2**4 + 37*R1**9*R2**5 + 289*R1**8*R2**6 + 1240*R1**7*R2**7 + 3185*R1**6*R2**8 +
            5005*R1**5*R2**9 + 4719*R1**4*R2**10 + 2508*R1**3*R2**11 + 660*R1**2*R2**12 + 65*R1*R2**13 + R2**14)

def N12(R1,R2):
    return (2*R1**11*R2**3 + 41*R1**10*R2**4 + 361*R1**9*R2**5 + 1785*R1**8*R2**6 + 5440*R1**7*R2**7 +
            10556*R1**6*R2**8 + 13013*R1**5*R2**9 + 9867*R1**4*R2**10 + 4290*R1**3*R2**11 + 935*R1**2*R2**12 + 77*R1*R2**13 + R2**14)

def N13(R1,R2):
    return (2*R1**12*R2**2 + 45*R1**11*R2**3 + 441*R1**10*R2**4 + 2470*R1**9*R2**5 + 8721*R1**8*R2**6 +
            20196*R1**7*R2**7 + 30940*R1**6*R2**8 + 30888*R1**5*R2**9 + 19305*R1**4*R2**10 + 7007*R1**3*R2**11 +
            1287*R1**2*R2**12 + 90*R1*R2**13 + R2**14)

def N14(R1,R2):
    return (2*R1**13*R2 + 49*R1**12*R2**2 + 529*R1**11*R2**3 + 3311*R1**10*R2**4 + 13300*R1**9*R2**5 +
            35853*R1**8*R2**6 + 65892*R1**7*R2**7 + 82212*R1**6*R2**8 + 68068*R1**5*R2**9 + 35750*R1**4*R2**10 +
            11011*R1**3*R2**11 + 1729*R1**2*R2**12 + 104*R1*R2**13 + R2**14)

def N15(R1,R2):

    return (2*R1**14 + 53*R1**13*R2 + 625*R1**12*R2**2 + 4324*R1**11*R2**3 + 19481*R1**10*R2**4 + 59983*R1**9*R2**5 +
            128877*R1**8*R2**6 + 193800*R1**7*R2**7 + 201552*R1**6*R2**8 + 140998*R1**5*R2**9 + 63206*R1**4*R2**10 +
            16744*R1**3*R2**11 + 2275*R1**2*R2**12 + 119*R1*R2**13 + R2**14)

def N2(R1,R2):
    return (2*R1*R2**13 + R2**14)

def N3(R1,R2):
    return (2*R1**2*R2**12 + 5*R1*R2**13 + R2**14)

def N4(R1,R2):
    return (2*R1**3*R2**11 + 9*R1**2*R2**12 + 9*R1*R2**13 + R2**14)

def N5(R1,R2):
    return (2*R1**4*R2**10 + 13*R1**3*R2**11 + 25*R1**2*R2**12 + 14*R1*R2**13 + R2**14)

def N6(R1,R2):
    return (2*R1**5*R2**9 + 17*R1**4*R2**10 + 49*R1**3*R2**11 + 55*R1**2*R2**12 + 20*R1*R2**13 + R2**14)

def N7(R1,R2):
    return (2*R1**6*R2**8 + 21*R1**5*R2**9 + 81*R1**4*R2**10 + 140*R1**3*R2**11 + 105*R1**2*R2**12 + 27*R1*R2**13 + R2**14)

def N8(R1,R2):
    return (2*R1**7*R2**7 + 25*R1**6*R2**8 + 121*R1**5*R2**9 + 285*R1**4*R2**10 + 336*R1**3*R2**11 +
            182*R1**2*R2**12 + 35*R1*R2**13 + R2**14)

def N9(R1,R2):
    return (2*R1**8*R2**6 + 29*R1**7*R2**7 + 169*R1**6*R2**8 + 506*R1**5*R2**9 + 825*R1**4*R2**10 + 714*R1**3*R2**11 +
            294*R1**2*R2**12 + 44*R1*R2**13 + R2**14)

#------------------------------------------------------------

def DAC15(number, r1, r2):
    D = Dr1r2(r1,r2)
    Ndim = [N15(r1,r2), N14(r1,r2), N13(r1,r2),
            N12(r1,r2), N11(r1,r2),
            N10(r1,r2), N9(r1,r2),
            N8(r1,r2), N7(r1,r2), N6(r1,r2),
            N5(r1,r2), N4(r1,r2), N3(r1,r2),
            N2(r1,r2), N1(r1,r2)]

    nstr = bin(number)[2:]
    nstr = '0'*(15-len(nstr)) + nstr

    number = [int(s)*n/D for s,n in zip(nstr, Ndim)]
    return sum(number)

#------------------------------------------------------------

r1 = 10e3
r2 = 20e3+50
v = DAC15(0x8000, r1, r2)
Vmax = 3.3

ddim = arange(0, 0x7fff, 0x10)
vdim = [DAC15(d,r1,r2)*Vmax for d in ddim]
odim = [d*Vmax/0x8000 for d in ddim]
edim = [v1-v2 for v1,v2 in zip(vdim, odim)]



plt.plot(ddim, edim, lw=3)

plt.xlabel("DAC(N)")
plt.ylabel("Voltage(V)")
plt.grid(True)
plt.tight_layout()
plt.show()


#------------------------------------------------------------
printf("\a")

#------------------------------------------------------------
#        END OF FILE : TEST3.PY
#******************************

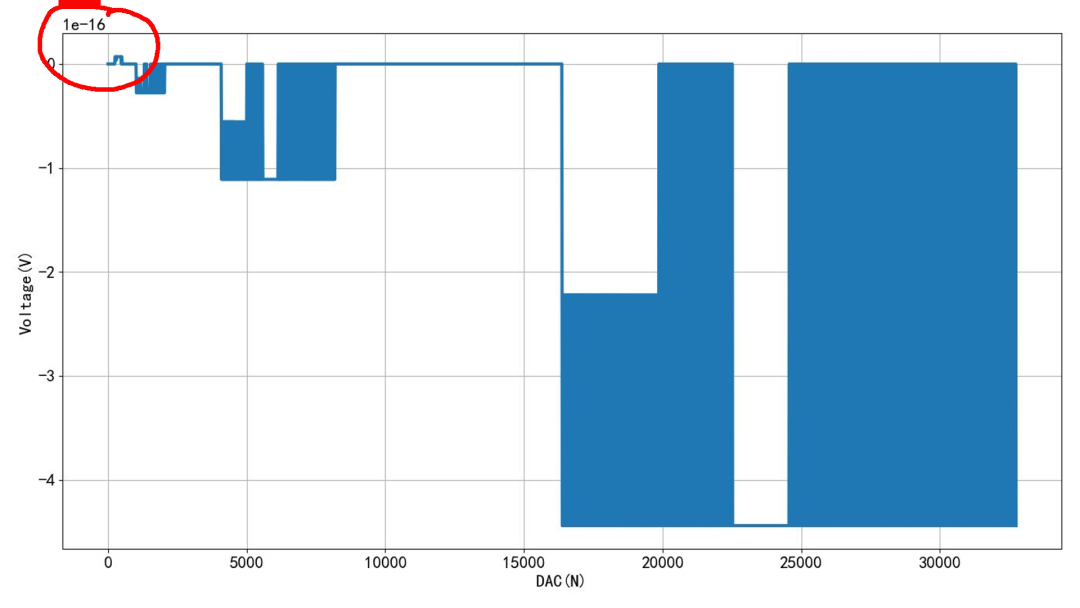
这是将R2增加了50欧姆，模拟单片机IO口输出电阻，计算出DAC输出的误差。可以看到这个误差的封装还是 13mV左右，与上午 8 通道对应的误差是一样的。这说明单片机 IO 口的电阻所引起的线性误差的绝对值和通道数量是没有关系的。

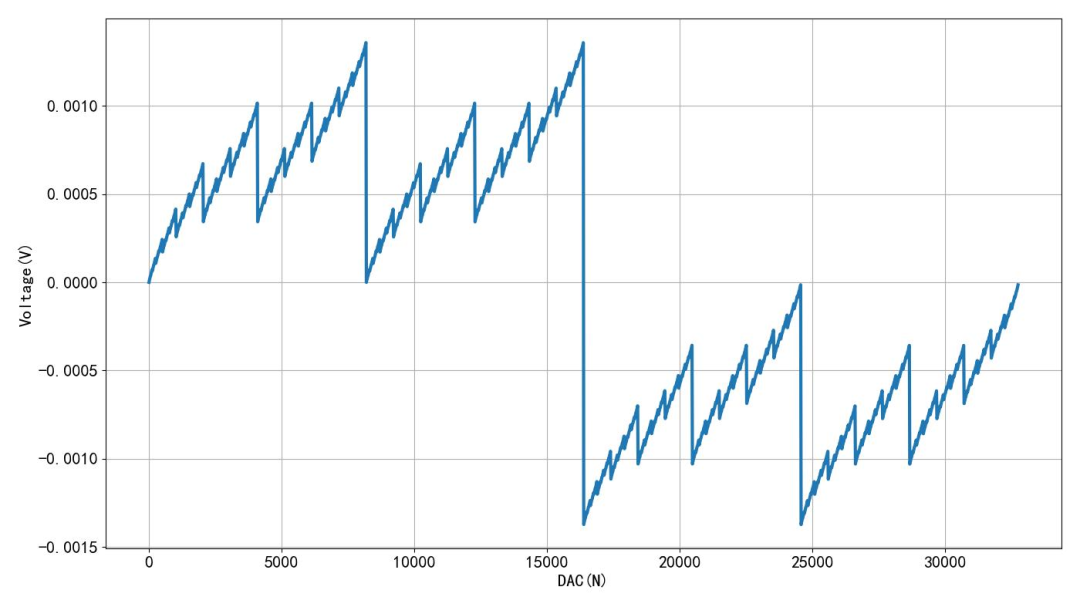
▲ 图1.2.2 将 R2增加50欧之后，输出线性误差

※ 总结 ※

本文对 15 比特电阻DAC 输出电压表达式进行了推导，通过对 R2电阻增加 50欧姆，计算出 DAC 的输出误差，验证了 R2R 电阻网络受到单片机IO口输出电阻的影响。误差的大小和通道数没有关系。这里仿真Python 程序和数据可以在 CSDN 文章中找到。这为之后对电阻DAC进一步的理论分析打下了基础。

登录阅读全文



免责声明：该内容由专栏作者授权发布或作者转载，目的在于传递更多信息，并不代表本网赞同其观点，本站亦不保证或承诺内容真实性等。若内容或图片侵犯您的权益，请及时联系本站删除。侵权投诉联系： nick.zong@aspencore.com！

TsinghuaJoking 这是一个公众号，它不端、不装，与你同游在课下、课上。卓晴博士，清华大学中央主楼 626A。010-62773349, 13501115467，zhuoqing@tsinghua.edu.cn

进入专栏

TsinghuaJoking 这是一个公众号，它不端、不装，与你同游在课下、课上。卓晴博士，清华大学中央主楼 626A。010-62773349, 13501115467，zhuoqing@tsinghua.edu.cn

文章：2250篇粉丝：87人

关注  私信

15bit电阻DAC输出公式

一、前言

二、推导过程

※ 总结 ※

最近文章

热门文章

推荐

最新资讯

15bit电阻DAC输出公式

一、前言

二、推导过程

※ 总 结 ※

最近文章

热门文章

推荐

最新资讯

※ 总结 ※