
计算下面各图所显示周期信号的傅里叶级数分解表达式,并绘制信号的双边频谱。要求。
1、写出三角形式傅里叶级数分解系数,包括 ;
2、写出复指数形式的傅里叶级数分解系数, ;
3、绘制出双边频谱( )。
(1) 第一小题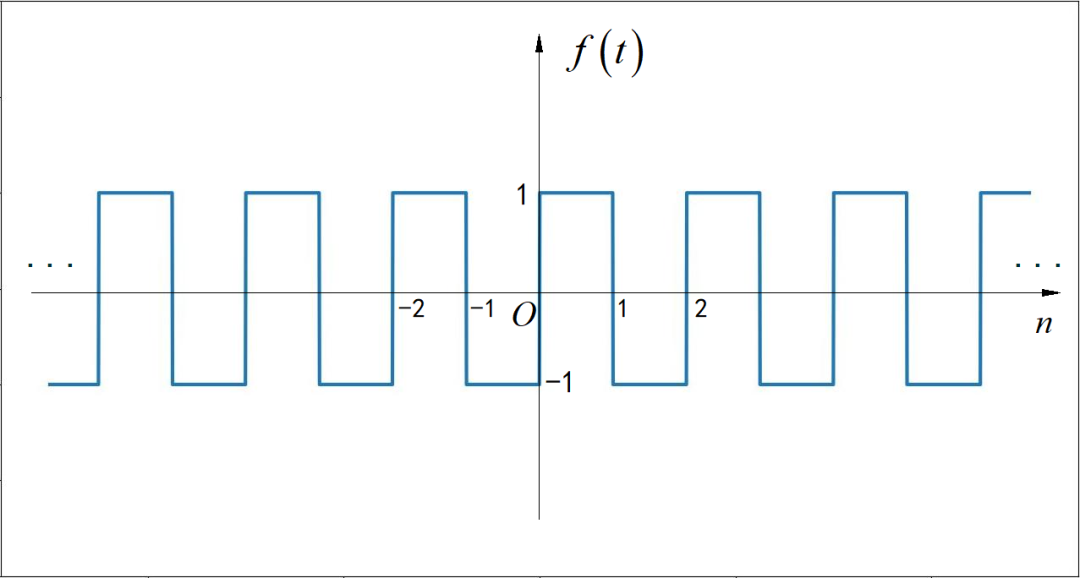
▲ 图1.1 周期信号第一小题(2)第二小题
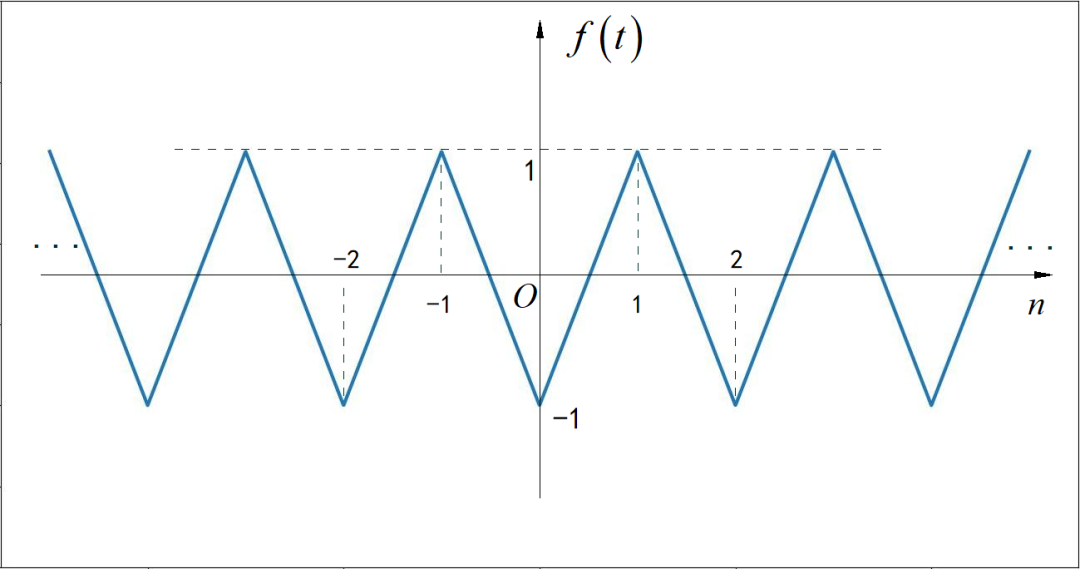
▲ 图1.1.2 周期信号第二小题(3) 第三小题
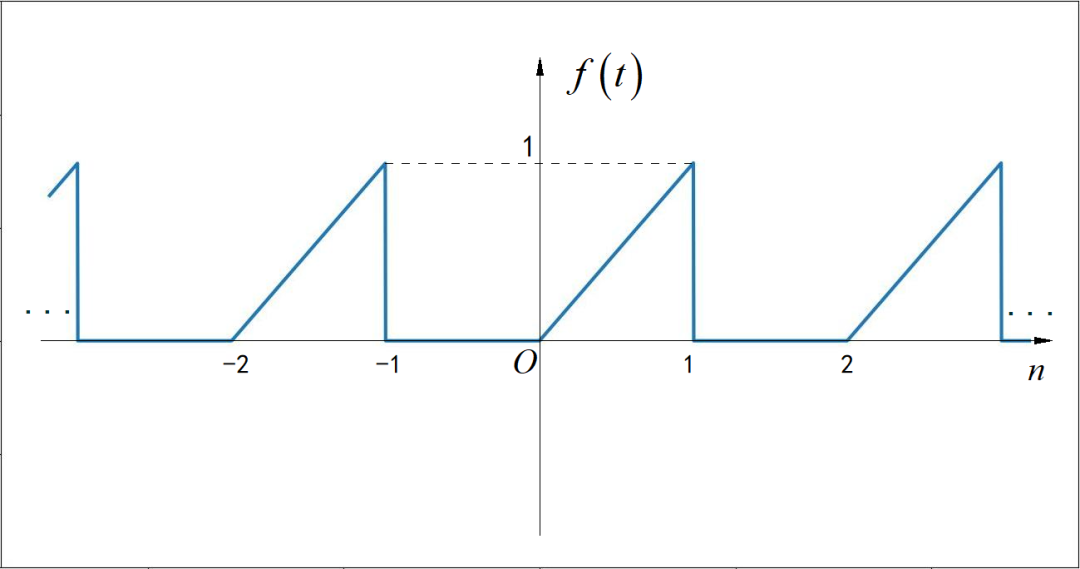
▲ 图1.1.3 周期信号第三小题(4) 第四小题
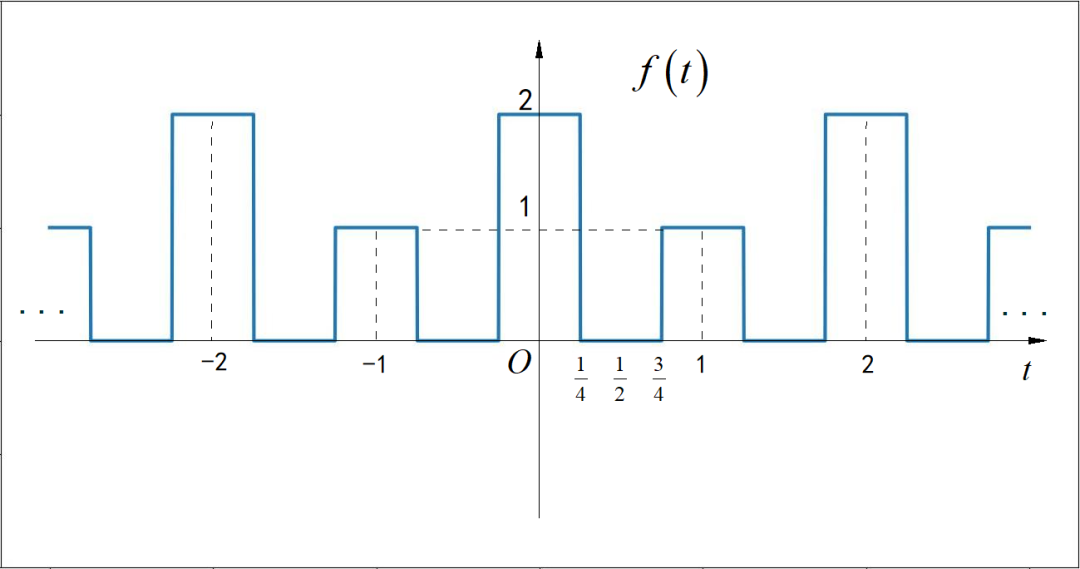
▲ 图1.1.4 周期信号第四小题 (5)第五小题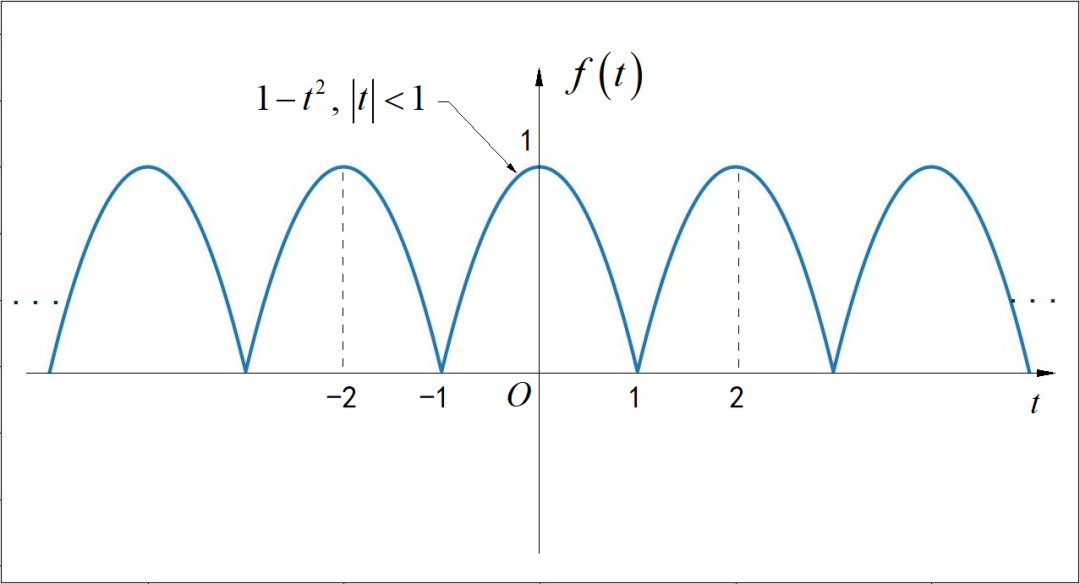
▲ 图1.1.5 周期信号五小题(6)第六小题
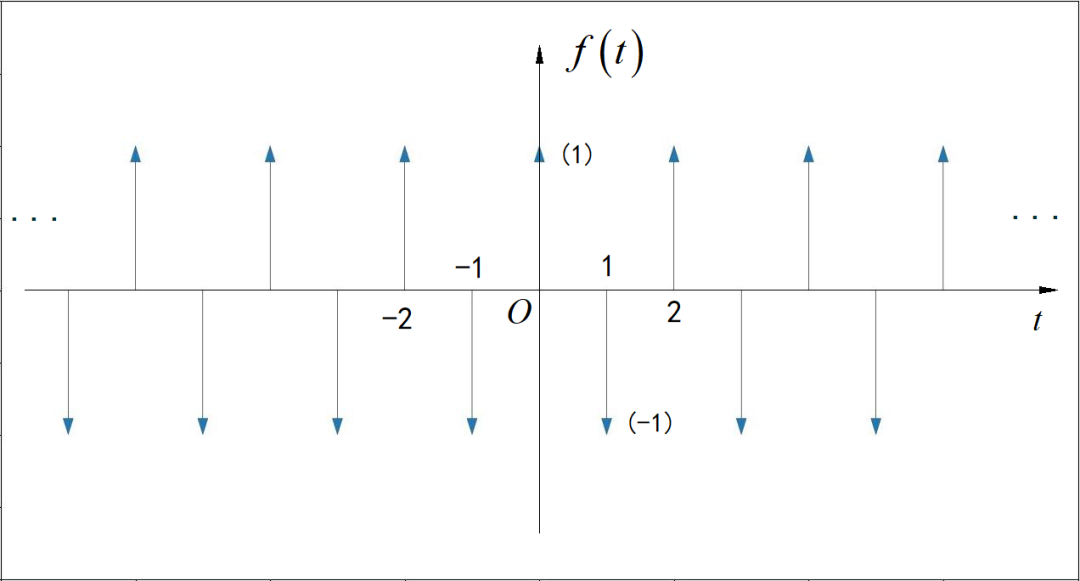
▲ 图1.1.6 周期信号六小题已知周期信号的数学表达式为:
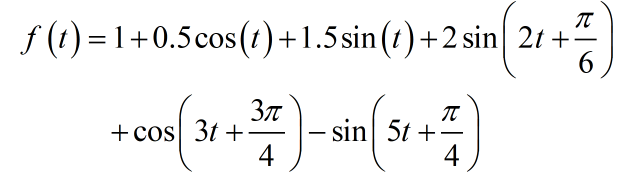
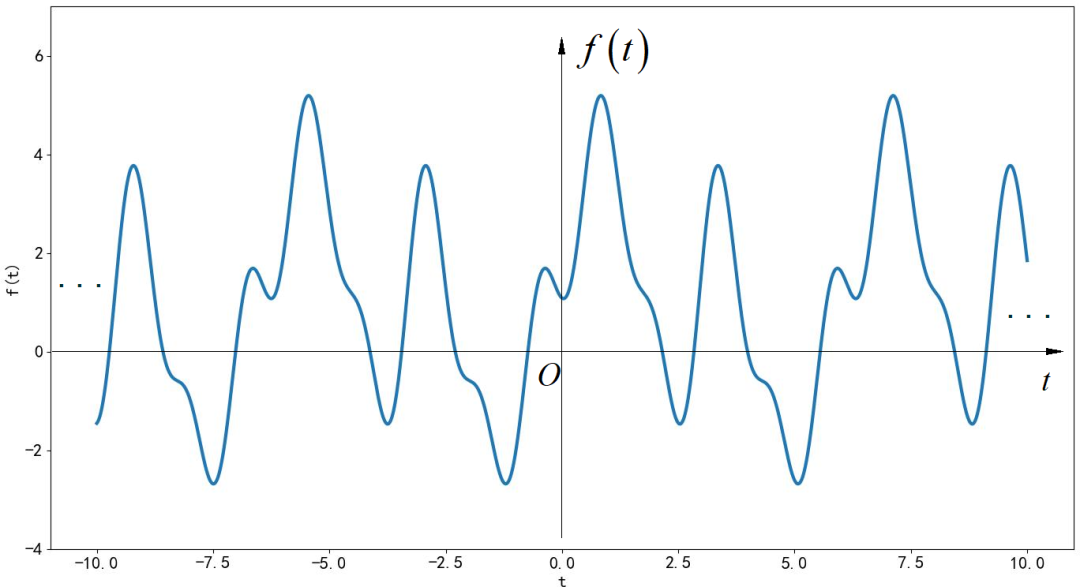
▲ 图1.1.7 信号的波形请绘制出信号的双边幅度谱和双边相位谱。
注:将上面公式分别展开三角,写出对应的复指数震荡信号形式的表达式。然后分别绘制出幅度谱和相位谱。相位取 之间。
已知周期信号 的波形如下图所示。请问该信号中是否存在如下频率分量?
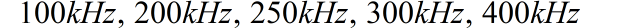
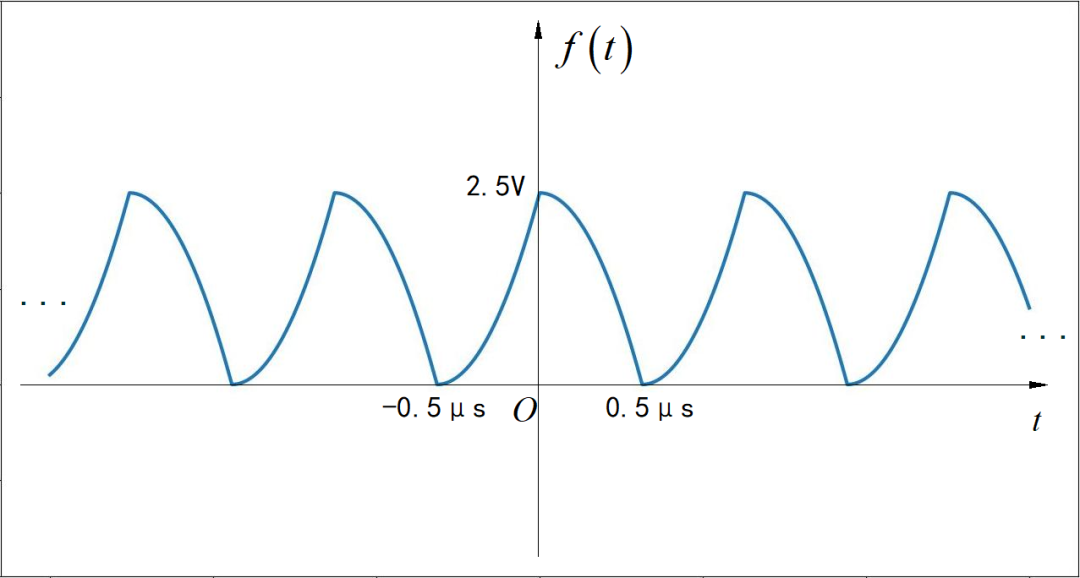
▲ 图1.2.1 电压信号波形请绘制出一个电路的示意图。将上面信号输入该电路,则在电路的输出信号中存在 的信号分量。
已知周期信号 在其四分之一周期内的波形如下图所示:
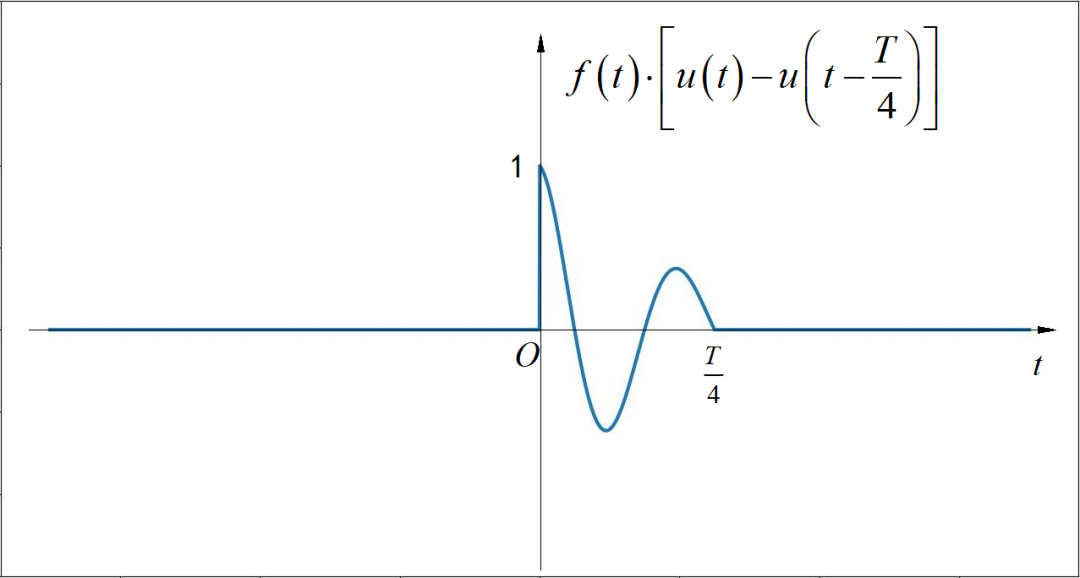
▲ 图1.2.2 信号四分之一周期的波形示意图下面给出了该信号中两种可能谐波分量存在的方式。针对每一种方式,绘制出该信号的一个完整周期内的波形。
(1) 信号为奇函数,只包含有奇次谐波;
(2) 信号为偶函数,只包含有偶次谐波;
注:下面两道小题都是选做题。
下面周期信号矩形脉冲信号,它的高电平为5V,低电平为 0V。频率未知,使用频谱仪 测量该信号,发现它的三的倍数次谐波(3,6,9,12....)都不存在了。请计算出该信号的直流分量是多少伏?
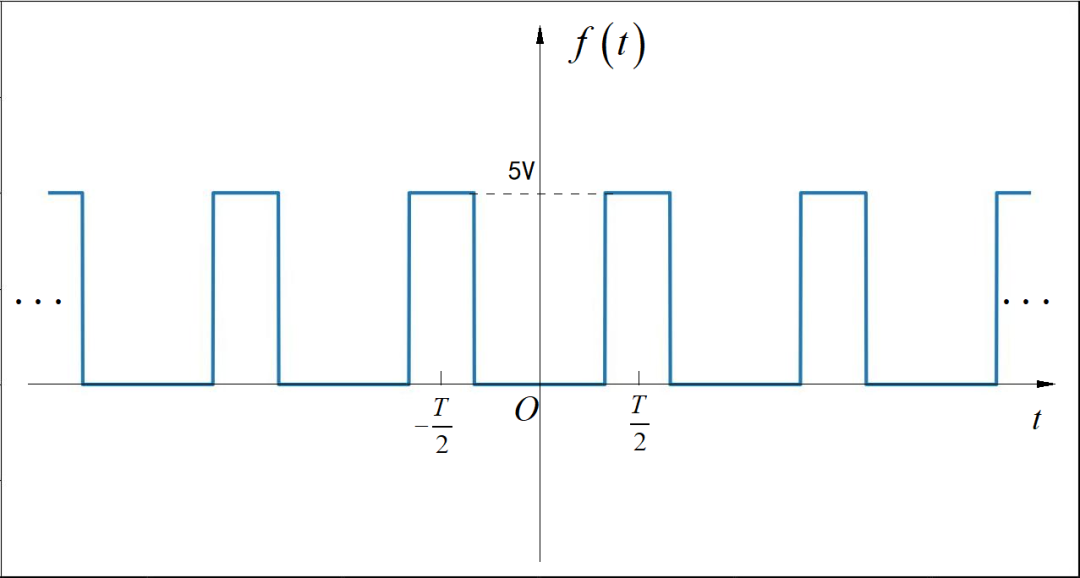
▲ 图1.2.3 周期方波信号提示: 首先根据该信号中 所有三次谐波不存在这个条件,推断出该信号的占空比。然后根据占空比再计算出信号的直流分量。
请设计一个信号波形,它的频谱中,不包含偶次谐波( ),也不包含三的倍数谐波( )。例如,下图所示的频谱中,只包含有 1, 5,7,11,13 等各个谐波分量,所有偶次谐波,三的倍数谐波都恰好为 0。
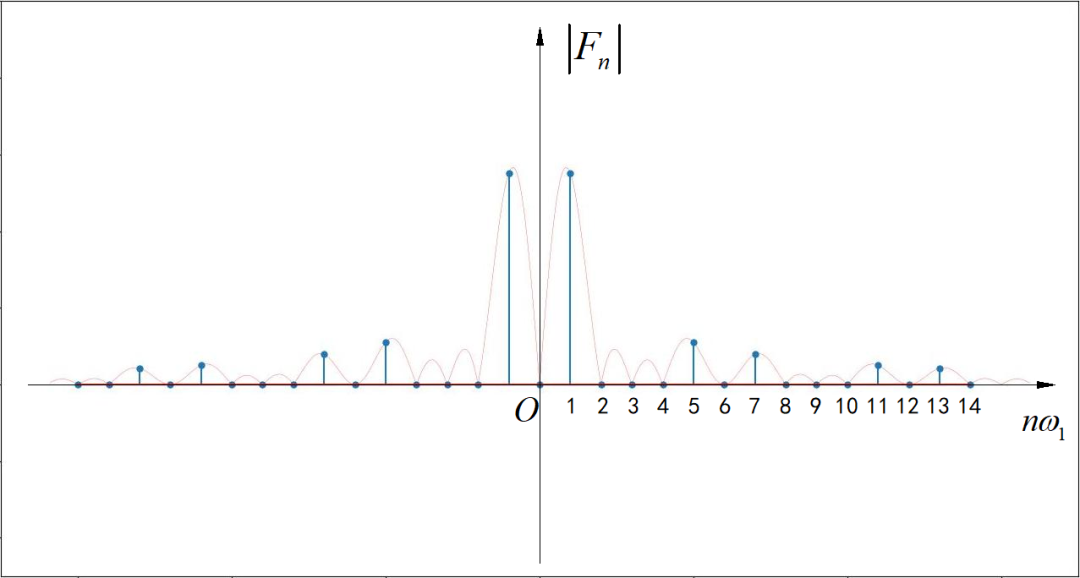
▲ 图1.2.4 信号的频谱提示:根据上面一道“求信号直流分量” 的波形,它不包含有三的倍数次谐波。然后在根据“奇谐信号” 的定义,通过将上面信号平移半个周期,然后减去原来的信号,就形成了奇谐信号。这样,这个信号就不包括偶次谐波,也不包含三的倍数次谐波了。
根据下面展示的周期信号波形特点,确定它们各自傅里叶级数中所包含的频率分量(sin、cos、奇次谐波分量、偶次谐波分量)。确定各自谐波分量衰减的规律,即谐波幅度随着 的增加大致衰减规律。
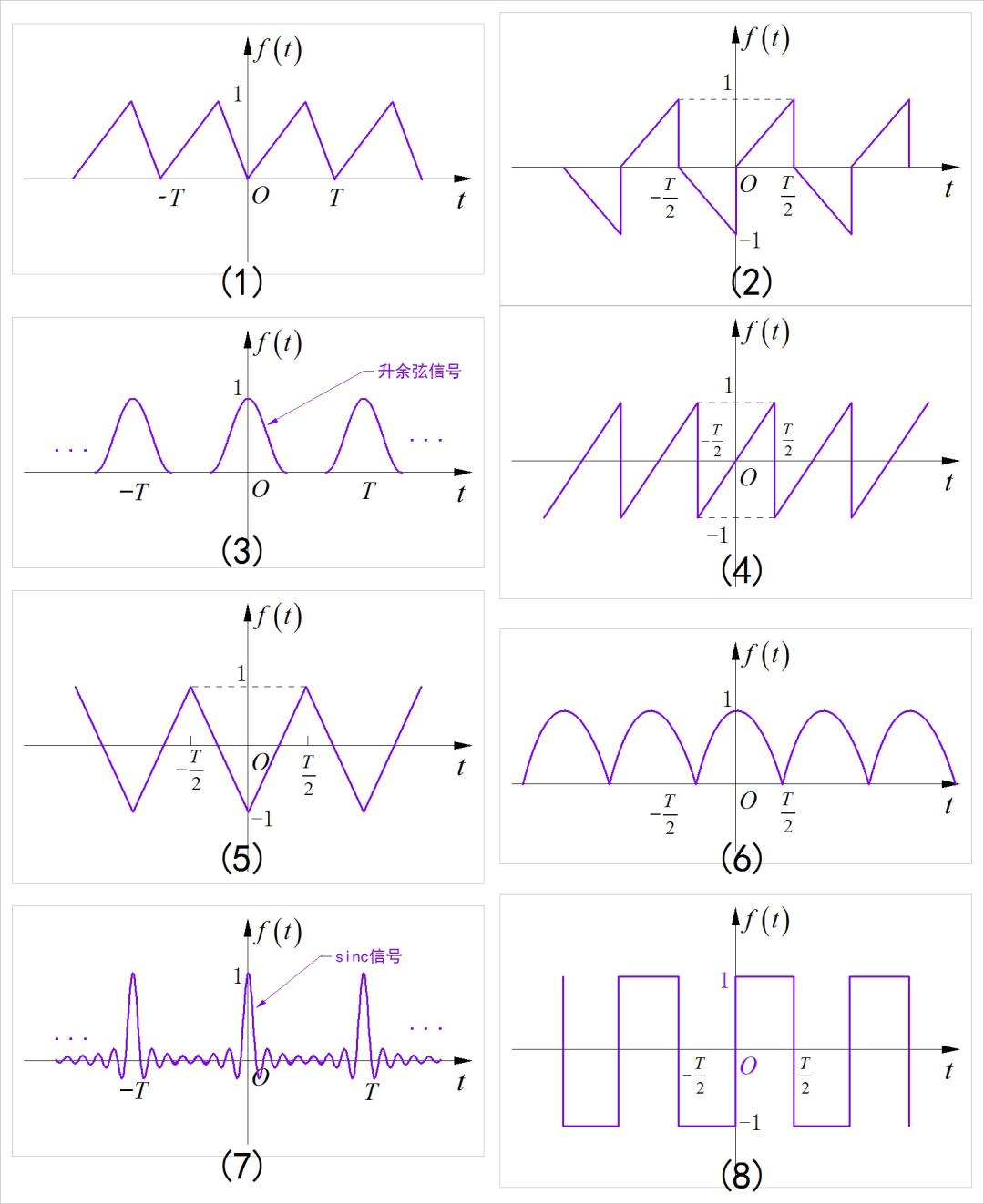
▲ 图1.2.4 八个周期信号的波形设 为 上的光滑函数,满足: 。信号 的傅里叶级数分解系数为 。信号 导数 对应的傅里叶级数分析系数为 。证明:
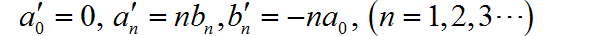
针对上一小题中的 ,假设 。假设 对应的复指数形式的傅里叶级数为 。证明 的傅里叶级数对应的系数 满足:

关于周期信号 的性质有如下的描述:
(1) 是实数信号;
(2) 的周期为 ,傅里叶级数分解中只存在 系数 ;
(3) 当 或者 时, ;
(4) ;
(5) 信号单个周期内的能量为:
(6) 大于 0。
如果 可以表示成: 。求上述表达式中的参数: 。
在MATLAB中,根据矩形周期脉冲信号傅里叶级数分解也锯齿波傅里叶级数分解的公式,绘制前N项级数叠加后的波形,体会在信号不连续部分出现的Gibbs现象。
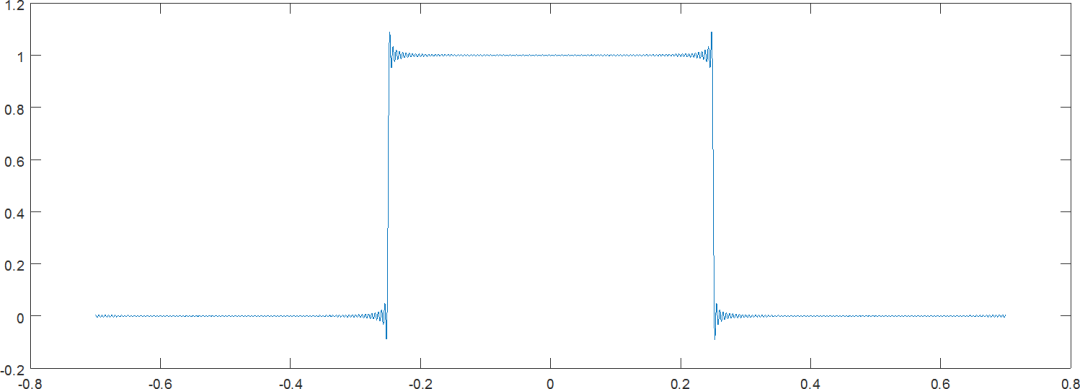
▲ 图2.1.1 利用N=200次之前的谐波合成的矩形周期信号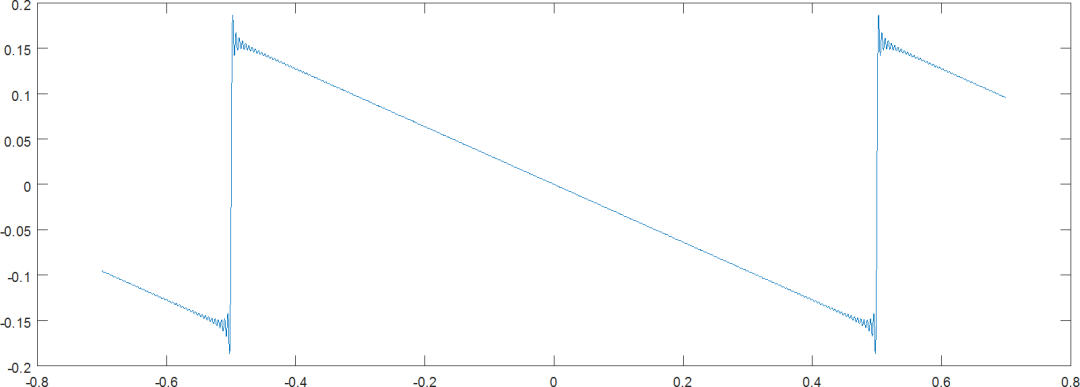
▲ 图2.1.2 利用N=200次之前的谐波合成的锯齿波信号提示:根据课件给出的矩形波、锯齿波谐波公式,计算对应谐波级数的合成波形。
无论是傅里叶级数分解,还是傅里叶变换,都存在Dirichlet 条件保证傅里叶技术分解(变化)收敛。其中要求信号在一个周期内(对于傅里叶变换要求在全部实数范围内)信号的:
下面分别给出了三个反例信号,分别对应面积无限、震荡次数无限、间断点个数无限。
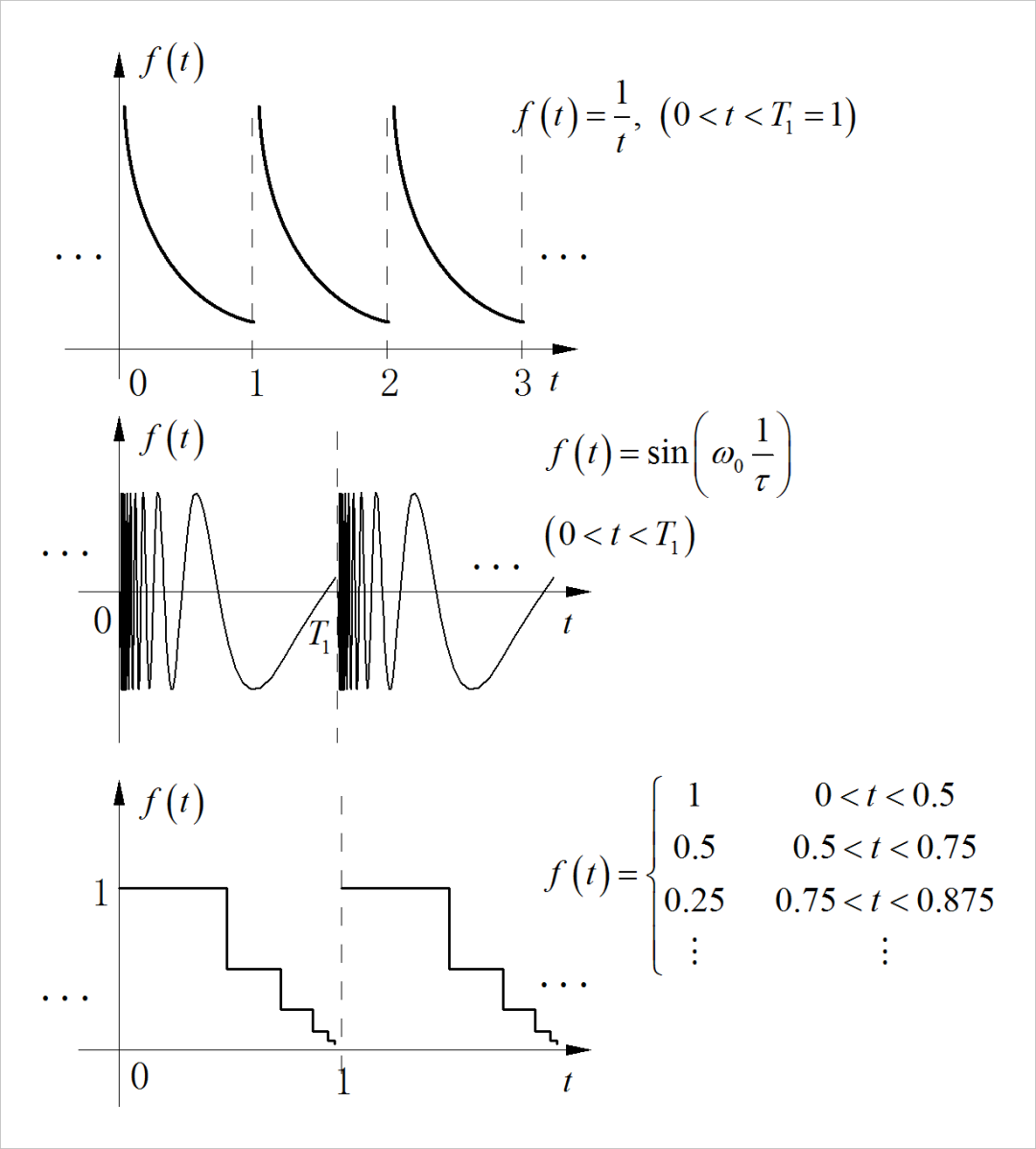
▲ 图2.2.1 三种不满足Dirichlet 波形条件的反例信号请利用Python,或者MATLAB通过数值计算的方式,观察上述三个反例信号它们的傅里叶级数分解的收敛特性。
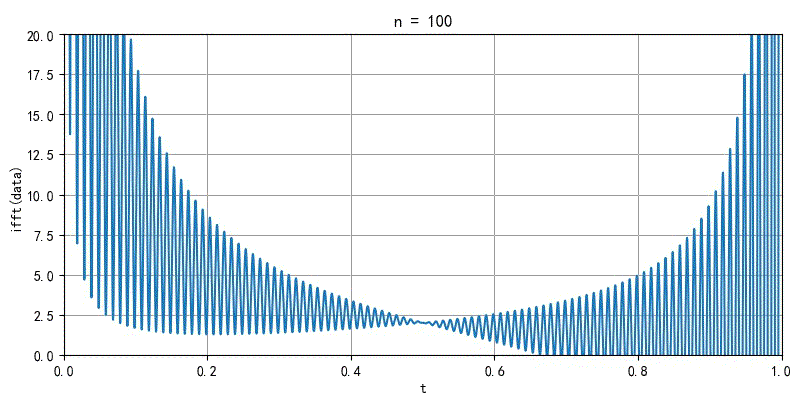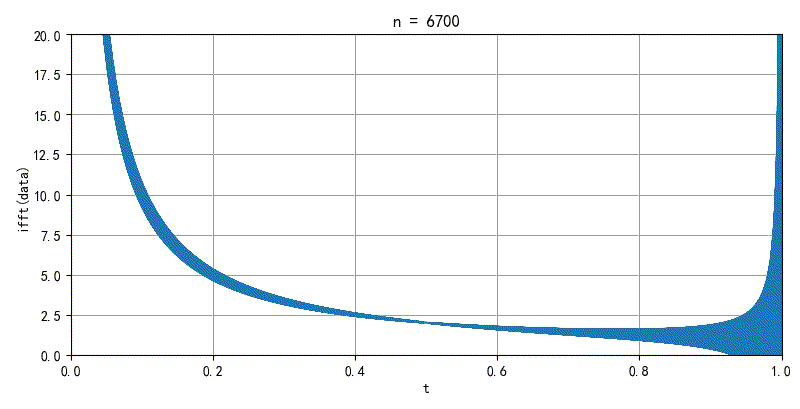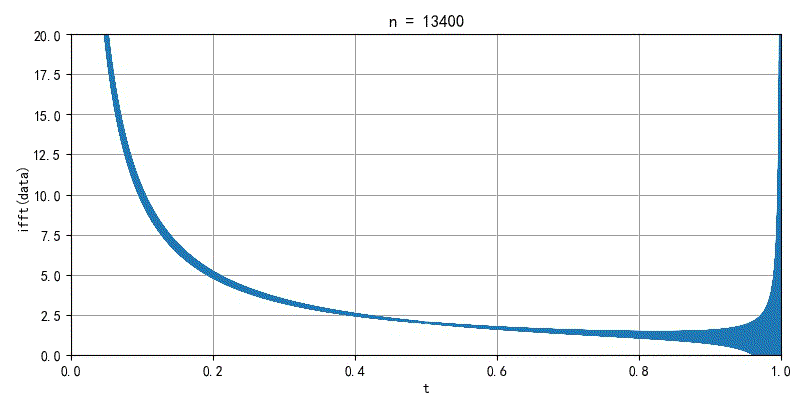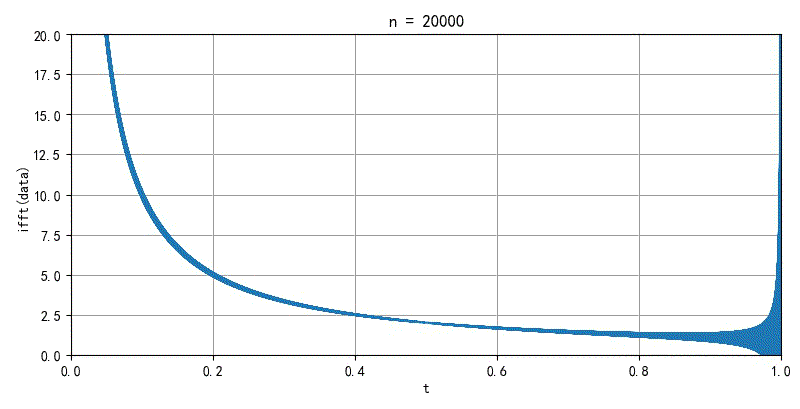
▲ 图2.2.2 面积无线的FFT前20000个系数重新合成信号的过程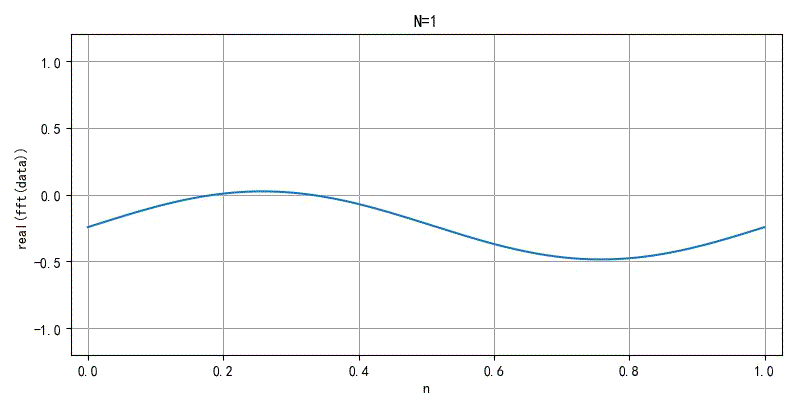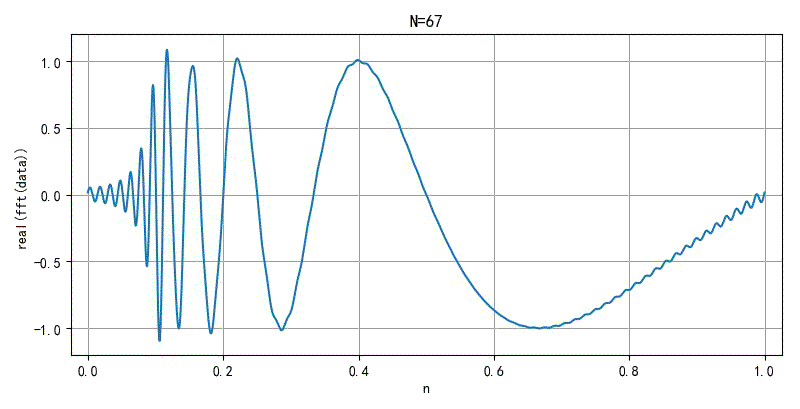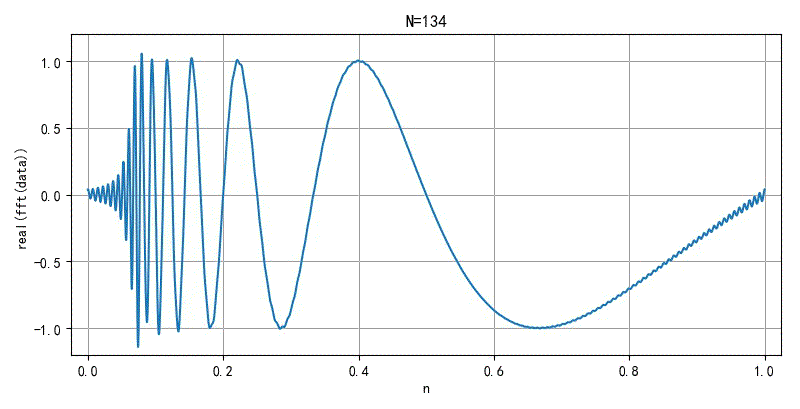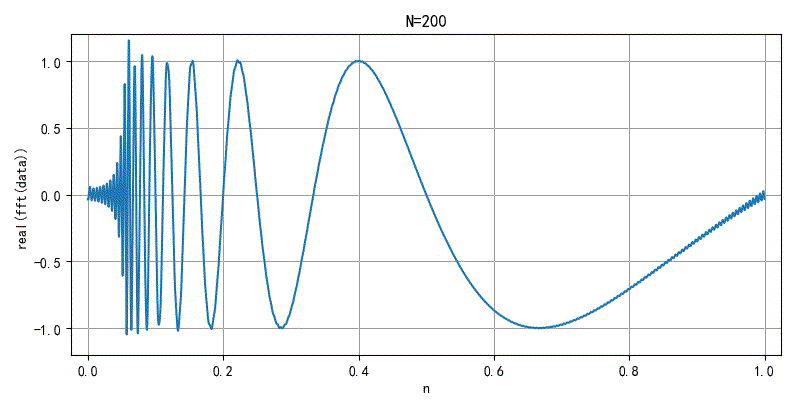
▲ 图2.2.2 无限间断点信号傅里叶级数收敛特性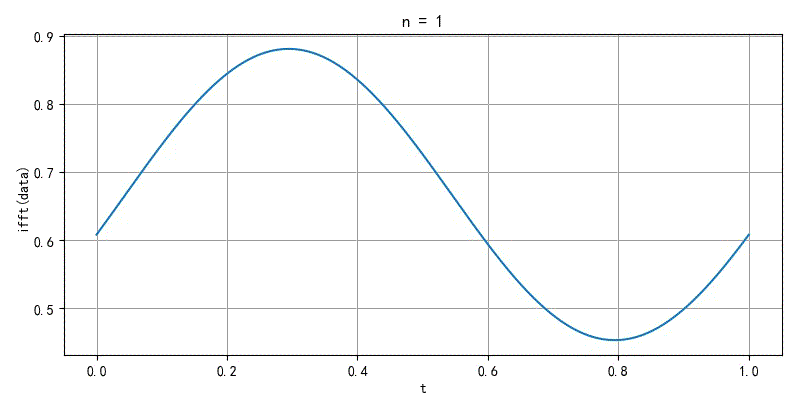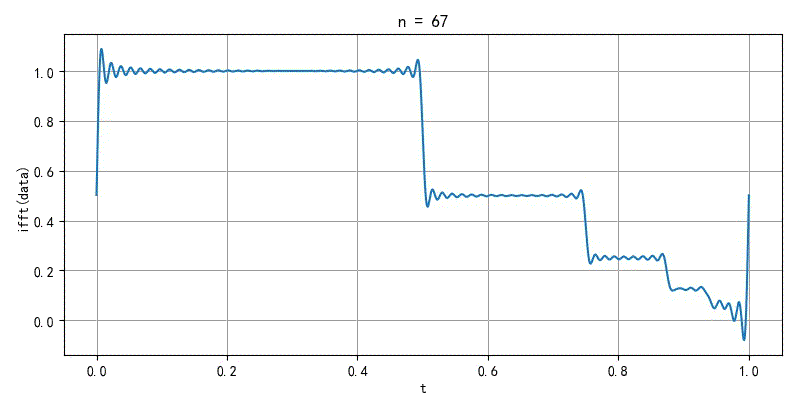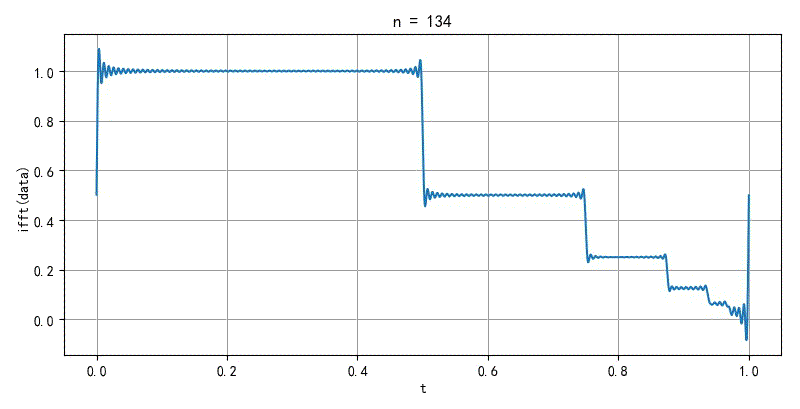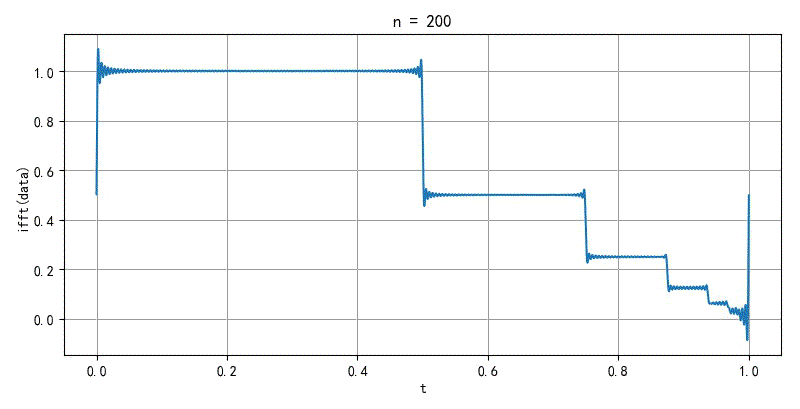
▲ 图2.2.2 无限间断点信号收敛特性利用Python编程,完成上述实验的参考方案可以查看CSDN 博文:傅里叶变换中的狄利克雷条件[2] :https://blog.csdn.net/zhuoqingjoking97298/article/details/115107590
信号与系统 2023(春季) 作业要求 - 第五次作业: https://zhuoqing.blog.csdn.net/article/details/129729625
[2]傅里叶变换中的狄利克雷条件: https://blog.csdn.net/zhuoqingjoking97298/article/details/115107590