上一篇-前菜篇,我们对PDM进行了一些头脑风暴,思考实验,并没有涉及具体的理论。但是我们发明了自己的PDM,核心思想是,进行抽象,用10数字流代表PDM,用窗口滑动平均,窗口内平均的1的密度来反映电压的高低。也留下了问题就是如何来编码满足我们这种需求?上一篇实际也大致介绍了思想,即差分思想,实际上我们现在应该能大概设计出这种算法了。
人总是习惯于直接的思维,就是直接给出需要的东西,但是对于计算机等其实这不一定是最好的方式。
我们先举个简单的例子来引出,类似我们前面进行的抽象,同样假设要告诉别人电压是多少,实际就是要告诉别人数字。
比如我手里有一串数字比如是5和10,要告诉别人,我们有不同的方式,首先是绝对值的方式,只要以下步骤
1.我手里有个5
2.我手里有个10
我们也可以是差分的方式,
假设开始以0为初始状态。
1.我手里有个比上一个数大5的数,即5。
2.我手里有个比上一个数大5的数,即10。
还不够,上述每次差分都是变化的,即每次都直接告诉对方差值,其实也可以固定一个幅度的差值。但是方向可以变,比如固定幅值为5,可以正和负,每次都只能告诉对方是+5还是-5,即只能告诉别人大了还是小了,大了就减小,小了就增大.
假设要告诉别人我手里有的值是0.
假设开始以0为初始状态。
1.手里的值是0,大于等于初始状态0, 告诉对方要+5. 这次行为记录为1.
2.此时双方记录的偏差的累积值是5(积分器累计偏差),这时我意识到往上偏了,我实际手里是0,而告诉别人是5,多告诉了,所以现在告诉别人要-5. 这次行为记录为0.
以上记录偏差需要积分器,知道多了还是少了要比较器,+5还是-5是反馈器。
3.此时值变为了5-5=0. 然后继续前面的过程。
所以记录的行为是告诉别人1010101010,即+5,-5的来回调整,最终平均下来就是+5和-5的次数一样,也就是平均值0.
实际上面我们就已经设计出来了,现在来画出其框图,很简单,无需再解释了。
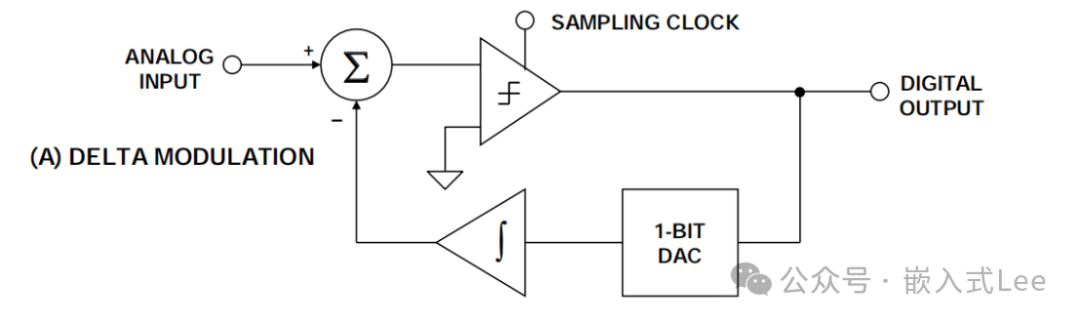
可以使用matlab的工具箱Delta sigma toolbox进行仿真。
ADI有一个在线网页可以形象的仿真每一步。可以对照上面的描述一步步去理解。
https://www.analog.com/en/design-center/interactive-design-tools/sigma-delta-adc-tutorial.html
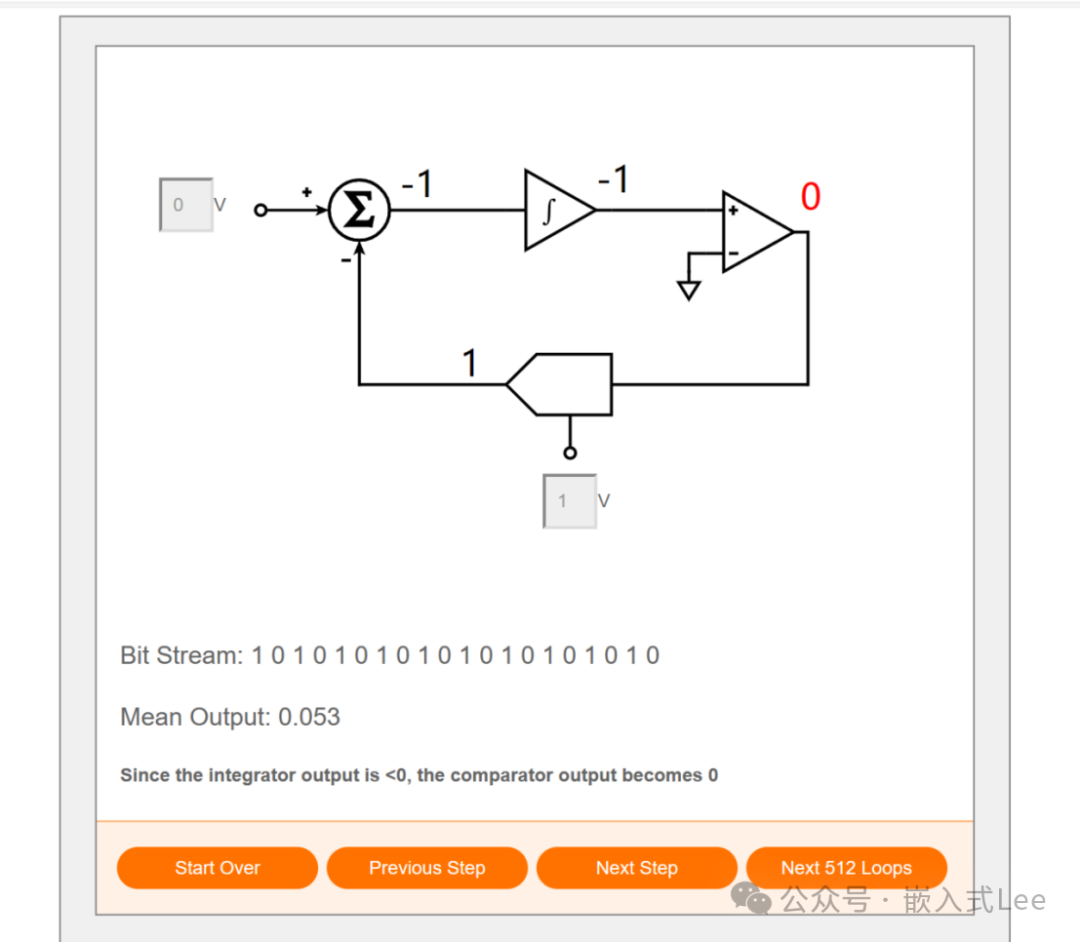
设置输入电压比如0V, 1bit D/A电压幅度1V。点击start over回到初始状态
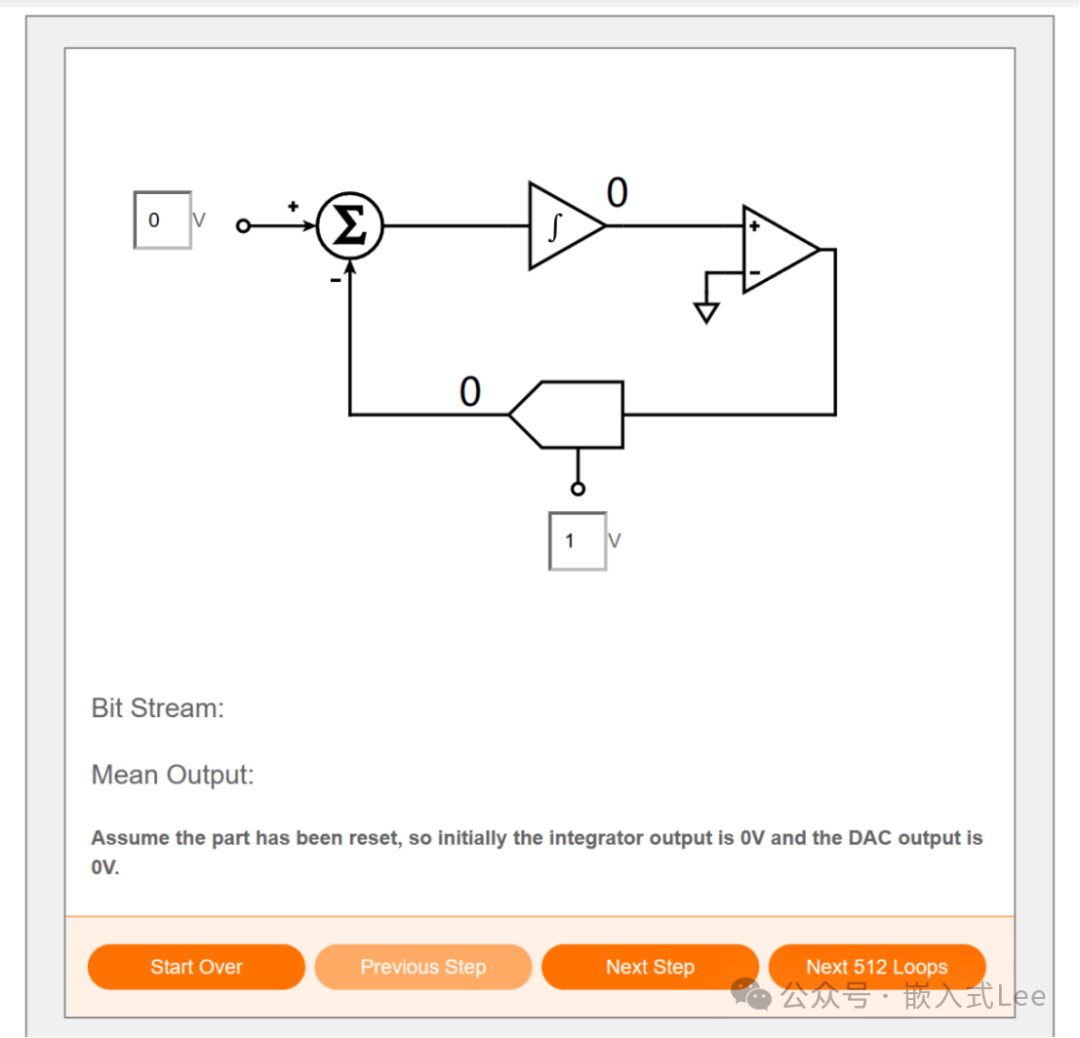
点击Next Step进入下一步,先计算偏差,输入为0,默认DA输出0,如下红色的偏差0,
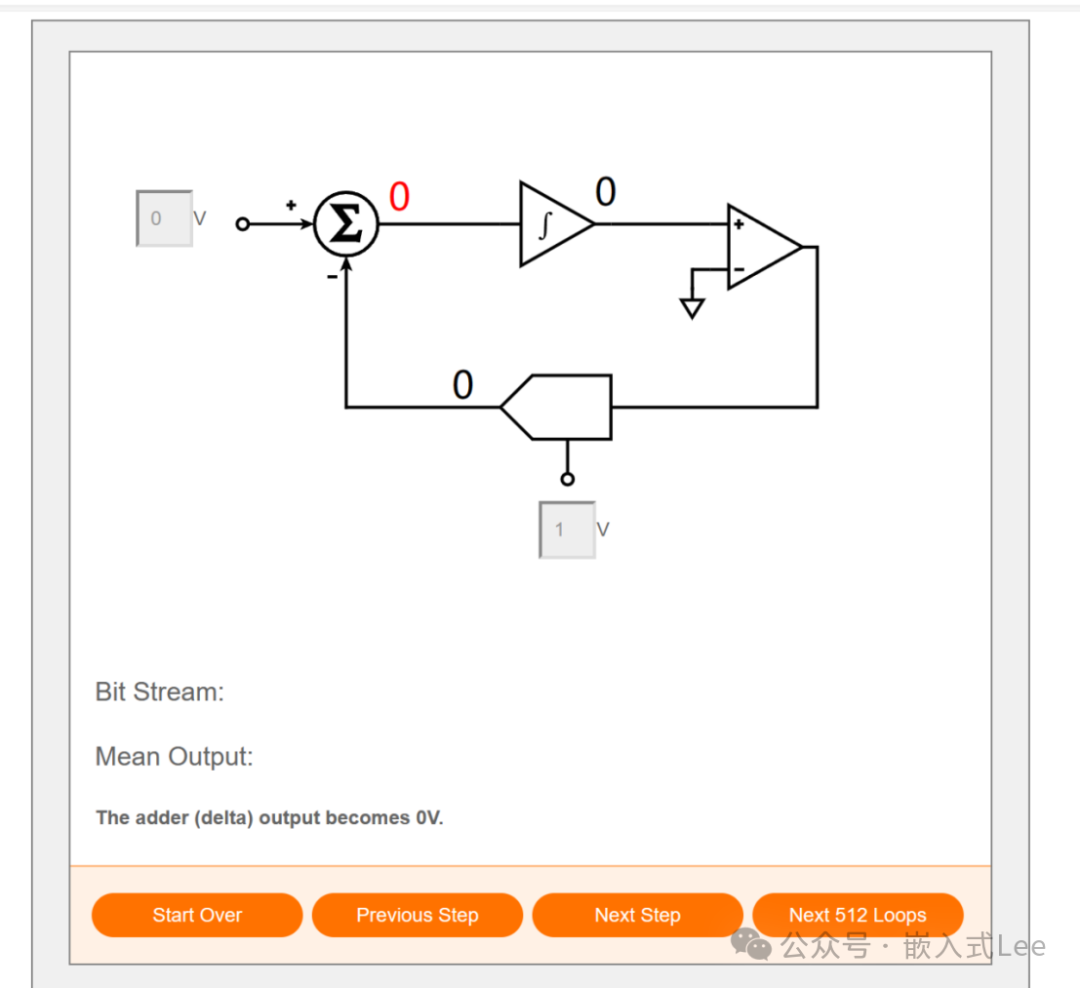
点击Next Step偏差积分为0
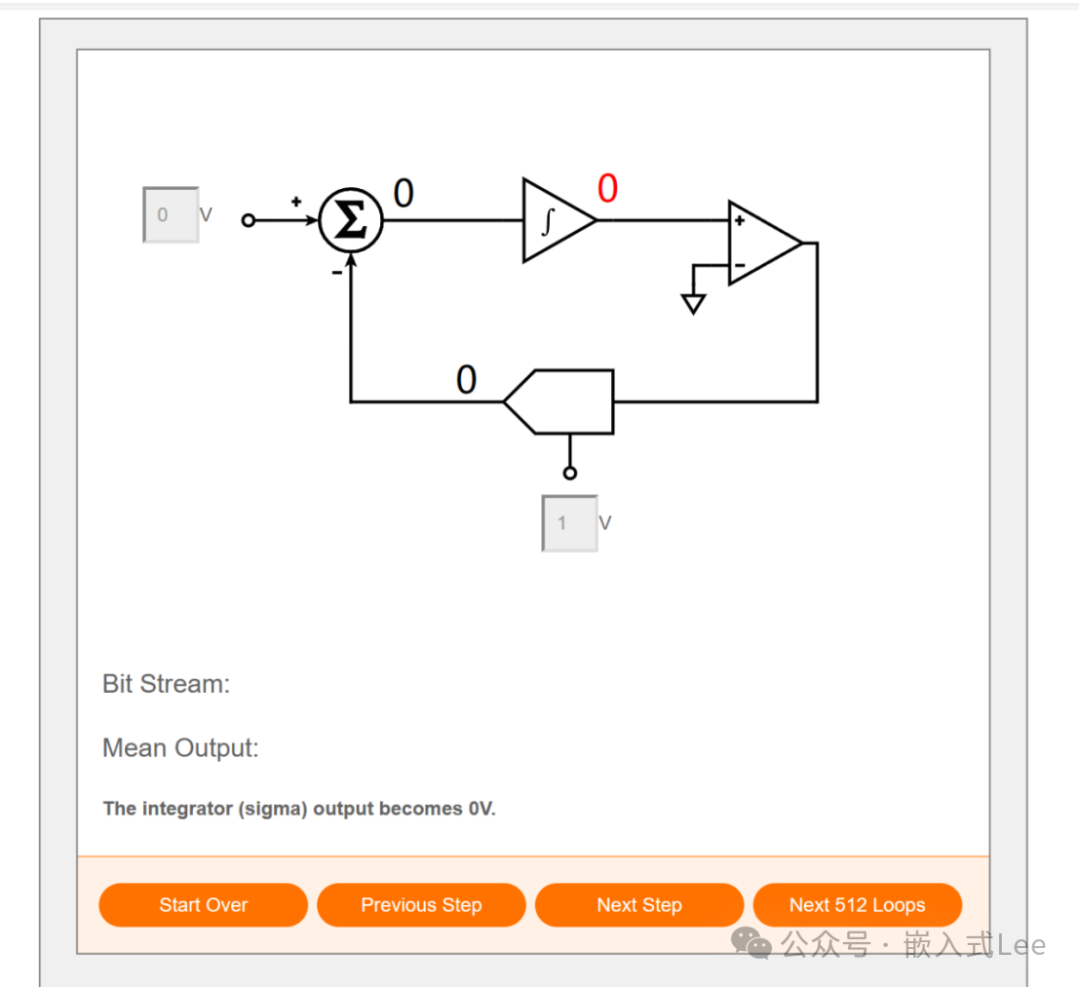
点击Next Step,比较器输出为1
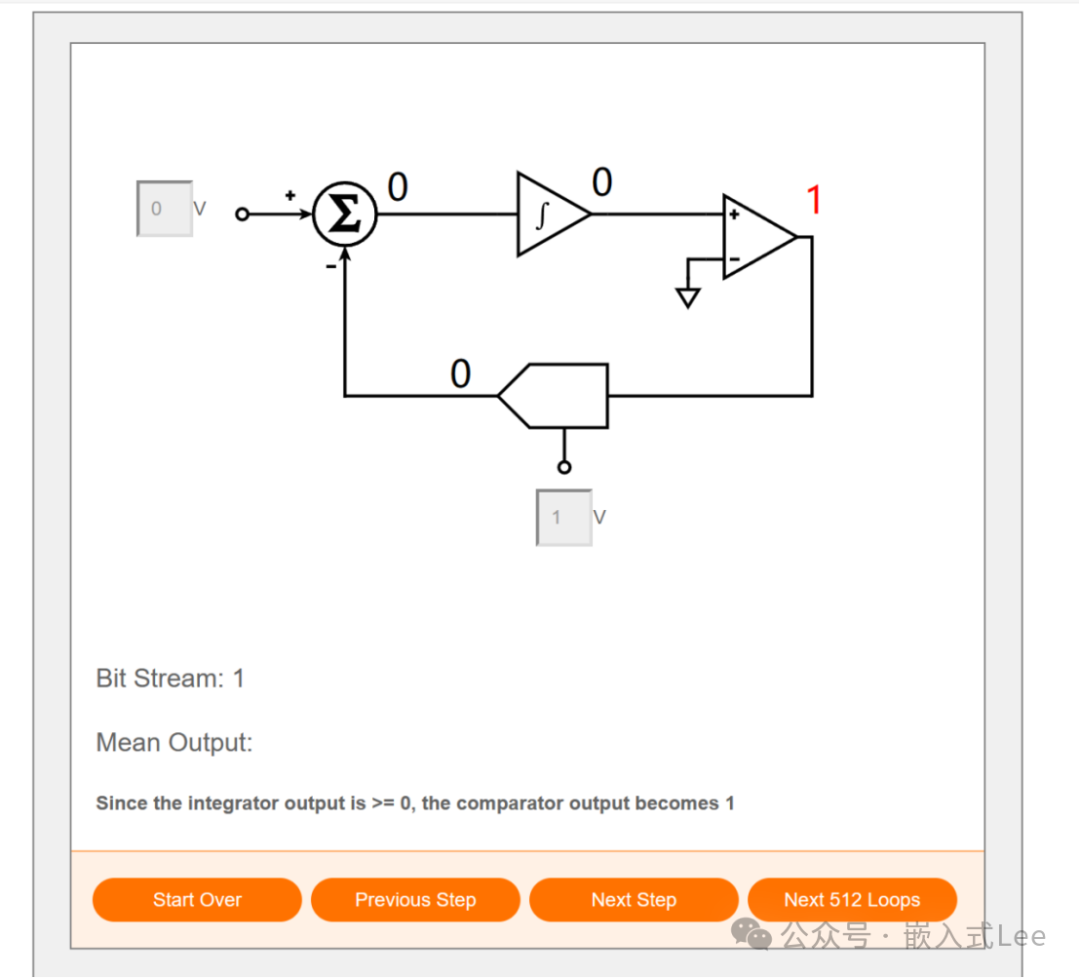
点击Next Step,比较器输出1,控制DA输出REF+即+1V
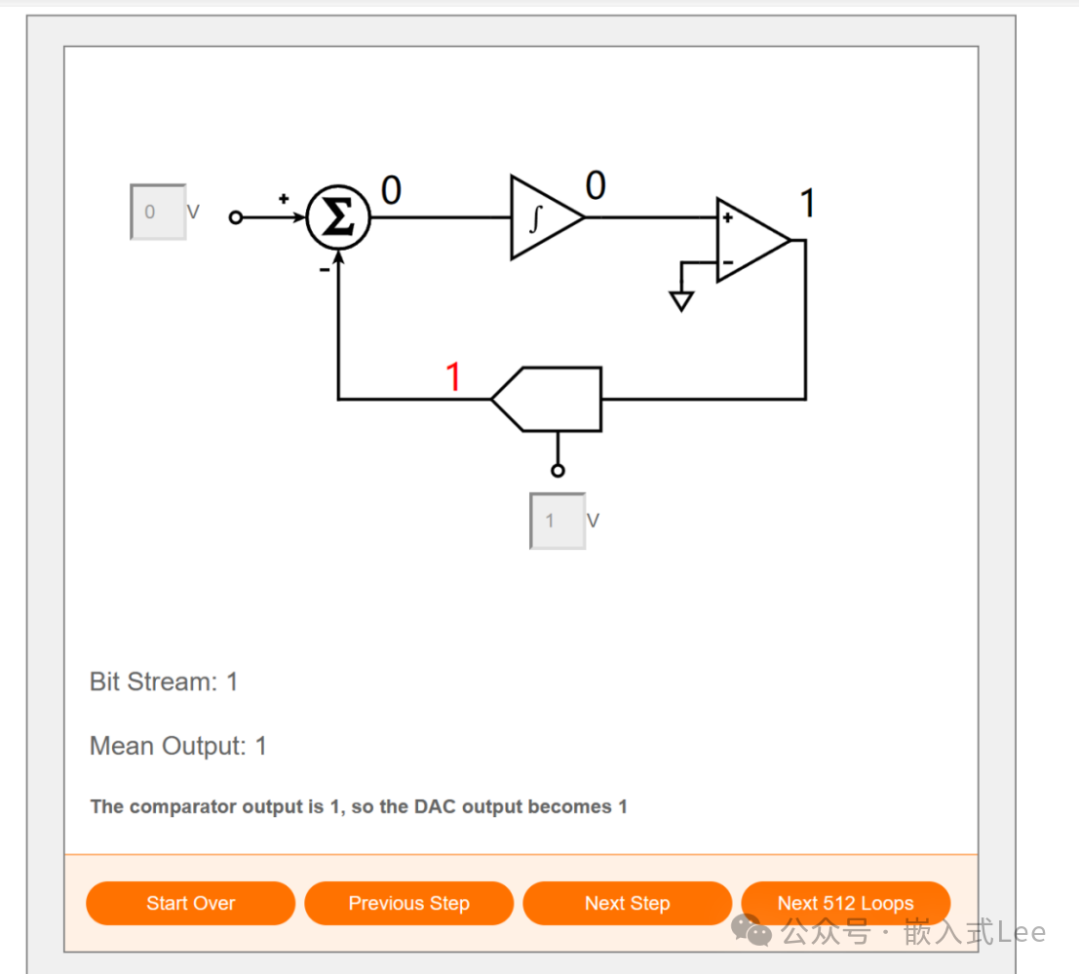
点击Next Step,计算新的偏差为-1
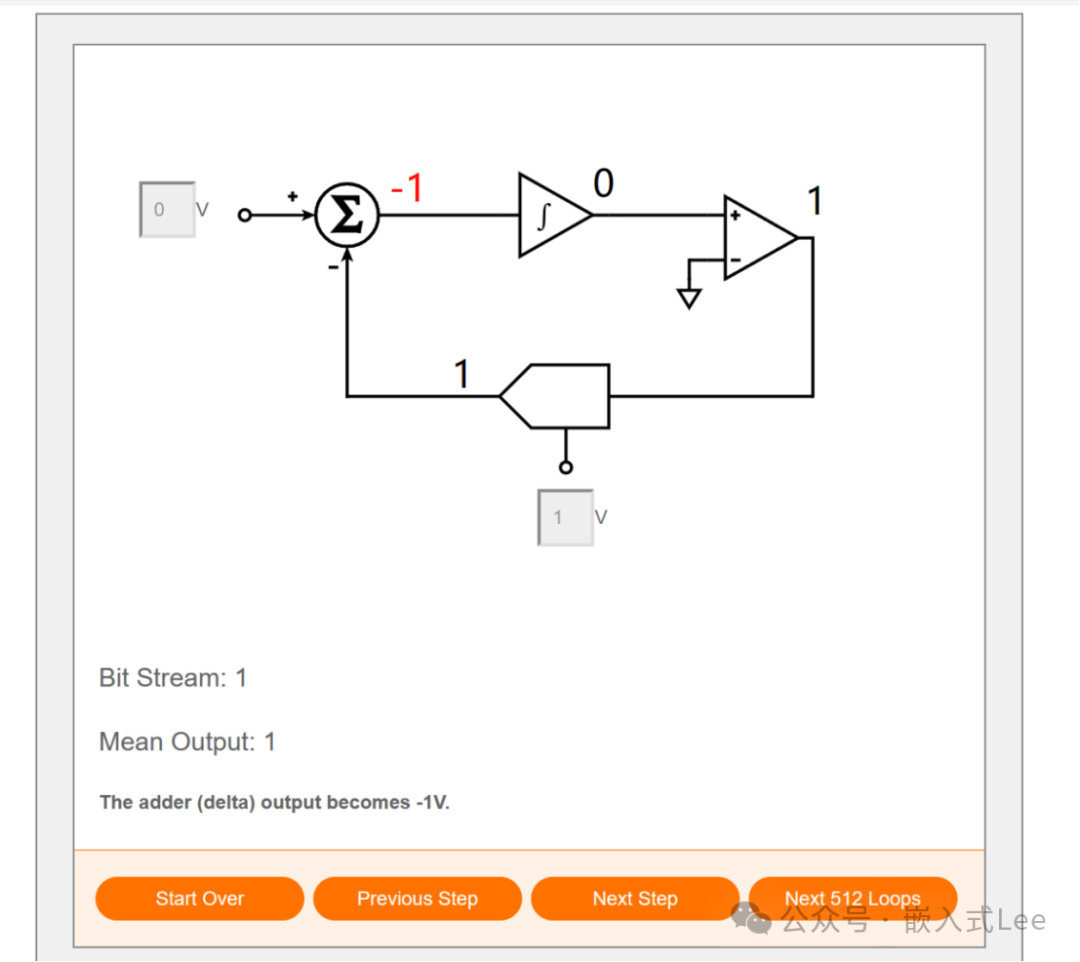
点击Next Step,对偏差积分0+-1=-1
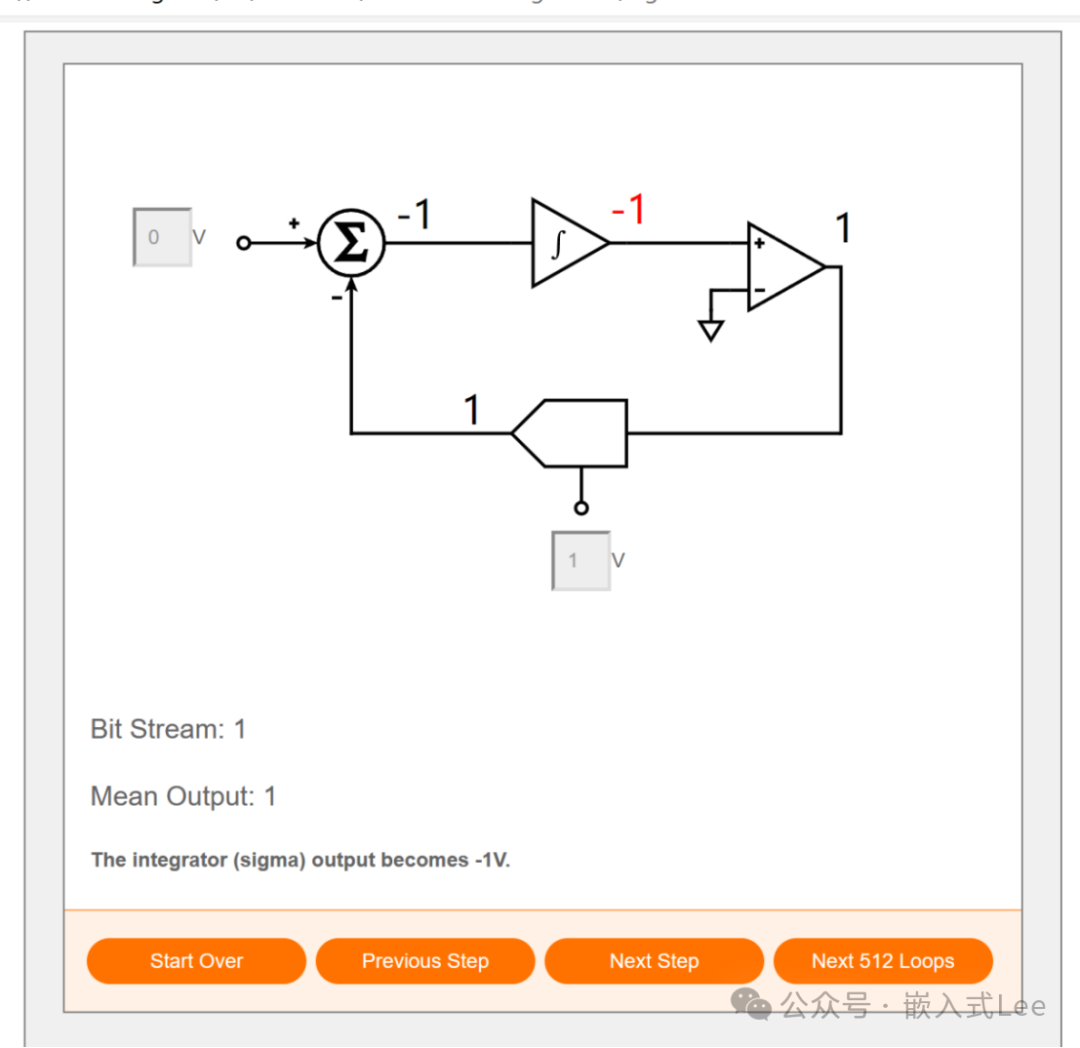
后面就是重复前面的步骤,
可以看到最后输出10101010的序列,计算20步之后是
10101010101010101010,即PDM编码,对应的就是1的密度为50%,即峰峰值的一半,即0V。
如果输入0.5,20步之后,1的个数为15/20即3/4, 即峰峰值的3/4, 即-1往上偏移2*3/4=-1+1.5=0.5.
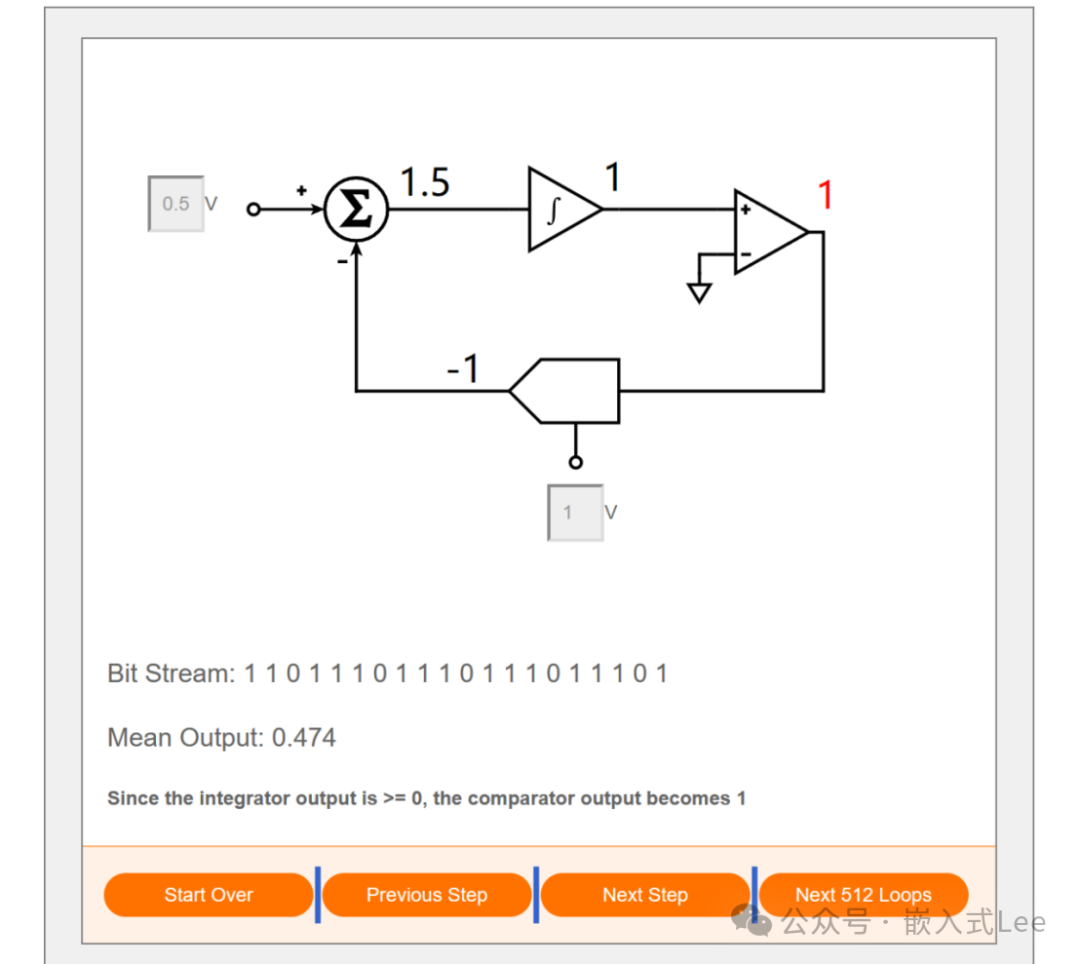
我们再来看上面的框图,可以看到对偏差进行积分,然后通过负反馈反向调整。这不就是理想运放的模型吗。
理想运放放大倍数无限大,所以只要有一丁点偏差就会触发后面比较器向偏差相反方向调整,通过DA要不就往+REF要不就往-REF调整。最终收敛可以偏差很小,也就是输出和输入的偏差很小,作为ADC采样就是采集的很准,这也就是sigma-delta可以做到24位甚至32位高精度的原因,但是他是用长时间的比较收敛来获得的,也就是长时间的平均来表示其值,所以采样率就低了,不适合采样高速信号,这就是这个世界总是充满矛盾的,没有这么完美。
一句话总结,哦豁,原来我们设计的PDM编码就是一个理想运放模型。
再来一句话总结, 哦豁,差分-反馈,大了就减小,小了就增大,三岁小孩都知道的道理,就这么简单。但是要保证偏差小精度大,就要很灵敏,即很小的偏差就要能检测到以决定如何调整,即放大倍数要大。
你看高深的技术,原来总是这么朴实无华,我们能发明PDM也就没什么奇怪的了。
但是,道理很简单,应用还是需要深入研究其原理的,我们从感性的认识到抽象的模型再到原理的分析,这样的步骤去理解会更透彻,而不是一上来就陷入莫名其妙的模型,算法,公式当中完全不知所云。后面我们会再从不同角度:时域,频域等角度去分析其特性,最终应用到实处,比如PDM播放音频的实践。