前面《UAC+PDM音频播放实践之-使用逻辑分析仪分析PDM信号》https://mp.weixin.qq.com/template/article/1711549811/index.html一文介绍了如何使用逻辑分析仪进行PDM分析。前面大概介绍了如何去判断一个PDM输出信号是否大致正确,涉及到了一些感性的理解,未涉及具体的原理。这一篇开始我们开始介绍PDM的原理。我们不一上来就摆公式,算法,而是依赖于自己的思考,问题,慢慢去引出相关概念,思想,原理。
所以本篇前菜篇,都是感性的思考,不涉及严格理论,重点在引出问题,引出思考,引出思想。
学习一个新的技术,个人觉得不需要一上来就陷入该技术的原理。而是先去思考一些问题,一项技术不会凭空产生,肯定是有其背景,所以自然而然我们会问这些问题:”这个新的技术为什么会出现?”,”这个新的技术出现是为了解决什么问题?”,”这个新的技术是基于什么旧的技术吗?”。面对新的内容,新的技术时刻问自己这些问题,然后自己先去思考,搜索资料,你会发现其实你也可以重新发明一遍这项技术,那么你才是真正的吸收了该项技术,真正学习到了其核心思想,这才是最重要的。一上来就上一堆公式,一堆原理的肯定根本没有理解其核心。
所以我们就以上述几个问题来问自己,然后去寻找答案。
我们看到PDM,脉冲密度调制,就去思考,查询其近亲,或者其先驱。自然很简单的大家都熟悉的PWM就映入眼帘了.PWM大家都知道,脉冲宽度调制,脉冲周期不变,宽度变化,即可等效于其平均电压不同,很简单的原理。
如下图:理想PWM,宽度可以0%~100%无极调整。
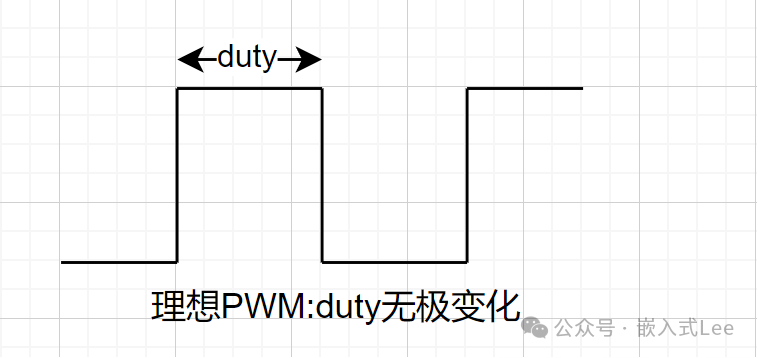
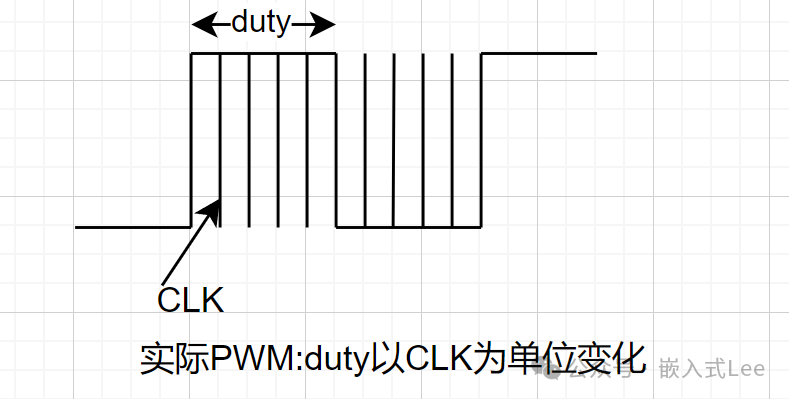
如果脉冲宽度可以无极变化,那么就可以实现电压的无极调整,当然实际这是不现实的。实际PWM是由时钟驱动的,时钟有最小的CLK单位,那么PWM的占空比调整颗粒度就是PWM的时钟颗粒度,无法无极调整。如果一个周期有1024个CLK,从0到1023,那么脉宽可以0到1023,即0%到100%,调整的分辨率是1/1024,即最多1024个等级。对应的就是分辨率是10位(2^10)。
如下图:实际PWM,宽度不能无极调整,颗粒度是1CLK。
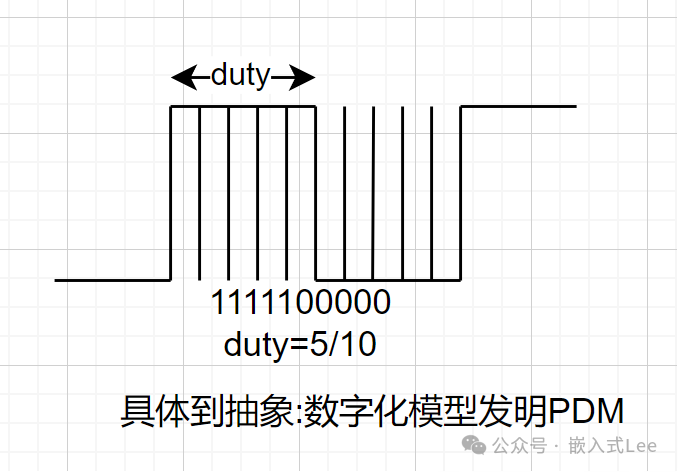
以上我们看到了PWM的颗粒度CLK,我们再换个角度来思考,我们来关注CLK,以CLK为单位进行划分,那么每个CLK对应的电平要么就是0,要么就是1,占空比就是1的个数的占比。转化为数字信号就是10序列。比如一个周期有10个CLK,占空比50%,对应的数字信号就是1111100000。实际上我们这里做了具体事务到抽象的过程,即脉冲宽度到01编码的抽象过程,具体到抽象,是进行一般分析的一般步骤,只有抽象才能找到一般规律。至此我们是不是可以给我们的这个抽象行为取个名字了,1的个数的比例代表不同的电压,比例不就是密度吗,那么就叫做脉冲密度调制吧,这不就是PDM吗,恭喜你就快要发明新的技术了,你看发明一项新的技术不就是这么简单朴实无华,只要自己多问几个为什么就自然而然能想到了。
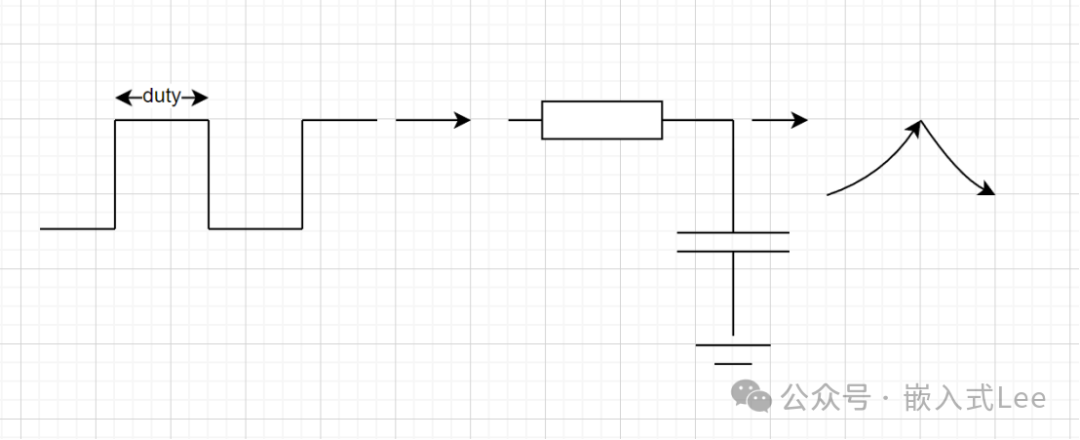
好的我们继续,我们上一节发明的PDM,不就是PWM吗,我们什么也没做,就是把PWM变为了10的序列来描述。没错这一小步就是创新发明的一大步,具体到抽象,这就是0到1的突破,后面才是1到99的优化。没错我们发明的PDM他就是PWM,这里先剧透一个结论”PWM就是特殊的PDM,就是频率不变的PDM”。别急慢慢来,任何一项技术都是要解决具体的问题的,我们来看看我们原来的PWM有什么问题。
PWM占空比能等效不同电压如下所示,PWM原始是一部分高,一部分低,这样不能实际使用,那么需要经过储能元件,电容来实现均衡。高时给电容充电,低时放电,这样就是后面的这种有脉动的形状,还不够理想,理想希望是一条直线,但是至少比原来好了。
从以上我们可以看出,充电和放电时间越长脉动越大,对于需要的比较均匀地输出不友好。此时我们可以调整电容的值来进行调整,输入源头PWM的周期大,即高和低都持续比较长时间时,可以电容大一点储能能力强一点,能长时间保持均衡,实际对应的就是对于低频信号,RC的低通滤波,截止频率为1/(2*PI*R*C),C增大就是截止频率降低,我们这里从更能直接感性理解的储能角度来说明。相应的PWM周期小,频率大,则电容可以小一点,这样可以快速充放电,快速响应变化,如果此时还用大电容,则来不及响应原始信号就变了,跟不上原始信号的变化,也就是截止频率为1/(2*PI*R*C),C减小就是截止频率增加,从频率角度看就是对于原始高频信号,截止频率也要高,避免滤掉了有效的高一些的频率成分。
以上我们知道我们的目的是要输出均匀的电压,即固定输入占空比,输出是一条直线。但是这是不可能的,电容储能也有充放电过程输出就有脉动。那么怎么减小脉动呢,那就从源头来看,原因是源头的高和低的持续时间,持续时间越大,越不利于均匀输出。那么怎么办,自然而然的就是减小这种持续时间,也就是将高和低均匀的分开。得益于我们之前的抽象PWM即对应10的序列,我们依然以50%的PWM为实例,原来是1111100000,我们重新排列为1010101010,这样不就是更均匀了吗。
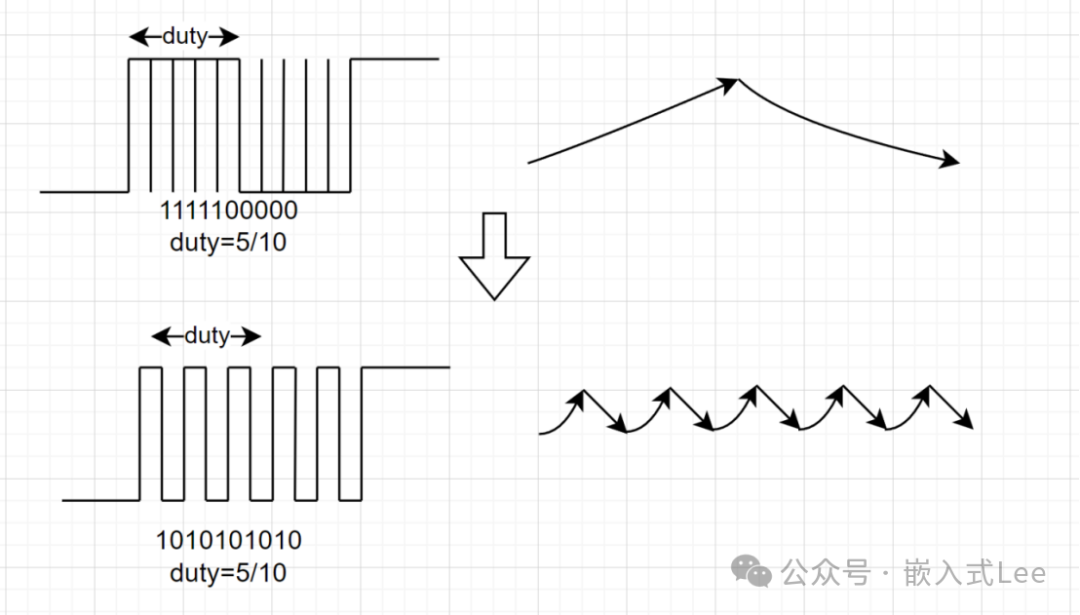
我们再仔细一看,哎不对呀,这不就是把频率变为原来的5倍了吗,不还是PWM吗?确实是,解决PWM波动的问题的一个思路就是增加PWM的频率,这里看起来就是变为了原来的5倍的频率,但是思想的本质是不一样的。不要小看我们这里111110000到1010101010的思想背后的魅力,这时0到1的一大步创新。
我们再来看依然是周期是10个CLK,占空比是3/10的情况呢,这时可以尽量让1均匀分布,就变为了1001001000,或者0100100100,可以看到他不是固定频率的PWM了,而是频率会变了,但是我们依然还是以1的个数占的比例来等效电压。所以现在问题变为了给定一个占空比即一个1的比例,如何去分配这些1,我们将原来的问题抽象为了一个数学问题,而这个即PDM编码算法,我们后面再讲。这一篇都是从简单的感性思考层面去考虑。
我们继续来优化我们发明的PDM。
我们前面看到PWM是以一个PWM周期为单位进行等效的,哪怕你CLK单位很小,但是前后两个PWM的等效还是间隔为一个PWM周期,这样造成了不均匀。解决不均匀的一个方式就是细分我们前面已经应用了。既然我们已经建立了CLK为单位的10序列的数据流,那么我们理应想到以CLK为单位进行处理分析了,于是我们可以应用常用的窗口滑动平均的思路来分析了,即对数据流定一个窗口,每次流入1位然后流出1位,对这个窗口内的数据求1的占比不就等效于其等效电压吗,此时我们将电压平均的颗粒度降低到了CLK为单位,恭喜你又发明了PDM的过采样的思想!!!。
如下所示,原来10个bit等效一个电压,间隔10bit,现在还是10个比特等效一个电压,但是间隔一个bit,后面的更精细,这就是所谓的过采样,即1个CLK就有一个等效电压。
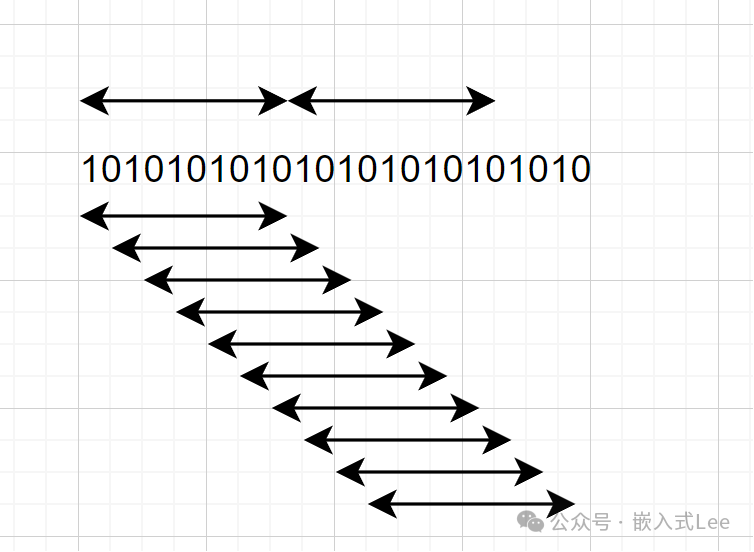
好的上面实际上我们已经知道如何根据一个PDM的数据流,大概去分析其对应的电压了,即框定一个窗口,数该窗口内的1比例,一次推进1位。

比如如下示例
0101011011110111111111111111111111011111101101101010100100100000010000000000000000000001000010010101
由于要表示正负数,我们可以设置一个偏置,即占空比50%处即中间电压处为0,此时1和0的密度相同即类似于101010序列,而负数我们对应于0~50%的电压,即0的比例高,比如负的最大值对应于0000序列,正数对应于50%~100%电压,即1的比例高,比如正的最大值对应于111序列。
我们手动对上序列人工解析,假如我们选择窗口范围是10(这里只是假设,实际是根据过采样大小,输入采样率确定的),那么前面我们计算的1的比例就如下,可以看到是正弦波的上升的部分。可以看到电压精度只有1/10,如果我们选择窗口范围更大则分辨率更高。我们看到输出的数据变为了每个CLK都有一个,这就是过采样了,实际我们可以抽取进行降采样,比如每隔3个选一个
010101101111011111111111111111111101 6/10 抽取
010101101111011111111111111111111101 7/10
010101101111011111111111111111111101 7/10
010101101111011111111111111111111101 7/10 抽取
010101101111011111111111111111111101 7/10
010101101111011111111111111111111101 8/10
010101101111011111111111111111111101 8/10 抽取
010101101111011111111111111111111101 8/10
010101101111011111111111111111111101 9/10 抽取
010101101111011111111111111111111101 9/10
所以要提高电压分辨率可以提高窗口的范围,即在更长时间范围内找1的比例,在1000个里面找分辨率就是1/1000,但是随之而来就是需要更多的时间去反应一个值,这样变化率就低了,无法跟踪快速变化的值,这就是PDM的缺点,矛盾永远是存在的。实际上我们利用了时间换精度,对于慢速变化的信号,我们可以在长时间内对其进行考察,以达到更高的精度和分辨率。
以上我们实际知道了数据流如何对应其电压值,那么我们现在的问题是已知电压如何编码数据流呢。 这里先剧透下实际就是1bitSigma-Delta ADC的原理了,也可以简单剧透下其思想,即使用差分思想,既然用1的密度来表示电压,那么我们就看当前值和目标值的差异,当前值小于目标值就增加一个1,提高电压,否则就减小一个1减小电压,最终会达到收敛,或者来回震荡,但是其平均值是收敛的。
比如用1代表正参考电压V+,0代表V-的参考电压,目标值是0即50%的电压。
如果当前编码是1即V+大于目标电压0,所以下一次输出0即V-的电压,对前面两次电压输出的积分0就是等效输出,即10代表(V+)+(V-)=0. 积分输出的电压再和输入信号比较,继续以上过程。利用运放负反馈的原理,只要反馈值和输入值有偏差就反向调整输出,最终保证输出和输入是一样的,即跟踪到了输入值。
这样输出10101010序列就代表等效电压0,即50%的电压。
从一项技术背后总结其核心才是最有意义的,才能举一反三为己所用,才真正的是学懂了才能得心应手的应用,并为自己打开思路。所以PDM实际给我们带来了一些有价值的思想,我们可以总结一下。
1.抽象,把具体问题抽象成模型,数学问题,来考虑,这是普通人和牛逼的人思考问题的最大的差别,也是有创新创造和无创新创造的人的最大区别。
2.细分,即微分思想。
3.差分, 即变化的思想,有时不需要知道绝对,知道变化即可,打了就减小,小了就增大思想就是这么简单。
4.均摊,窗口滑动的思想。
5.矛盾,时间换精度,从矛盾对立的角度寻找解决方案,一个方向走不通时考虑下其对立面,往往两个方向是相互的此消彼长。类似的有空间换效率等。
足够多的bit数取平均可以得到更精细的分辨率,但是更多的bit需要更长的时间,所以只能减少每个bit的时间,即增加频率。正因为该原因所以才使得其对于高频响应比较困难,高频采样和精度就是一对矛盾。