
信号与系统2024(春季)作业要求以及参考答案汇总[1]
信号与系统2024(春季)作业要求 - 第二次作业[2]
分别写出下面信号的直流分量与交流分量。
注: 交流分量可以使用原信号减去对应的直流分量来表示。
(1) 三角波信号
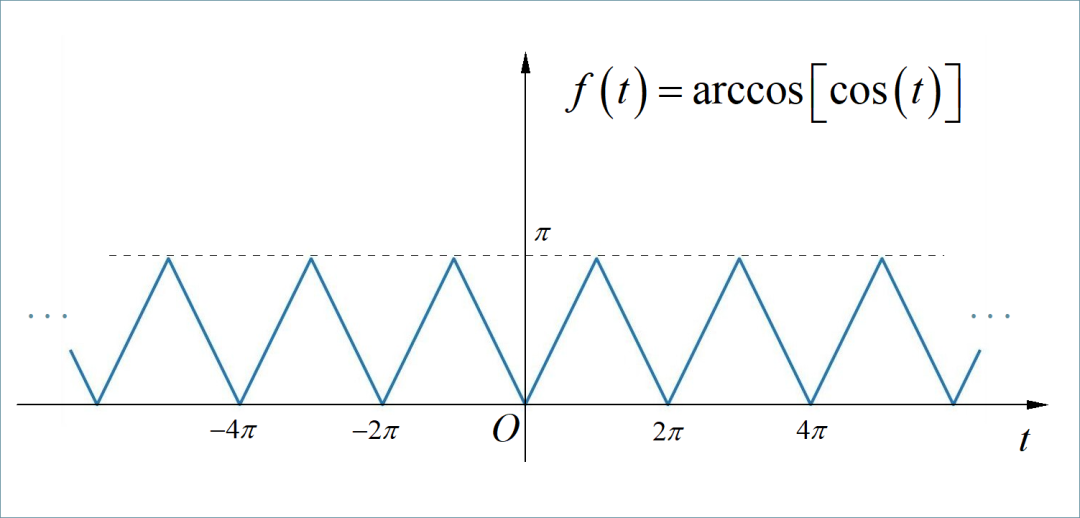
▲ 图1.1.1 周期三角信号□ 解答:
这是一个周期对称三角波信号,它的直流分量是一个周期内信号的平均值。根据波形参数,可以分别求出对应的直流分量和交流分量。
(2) 半波整流信号
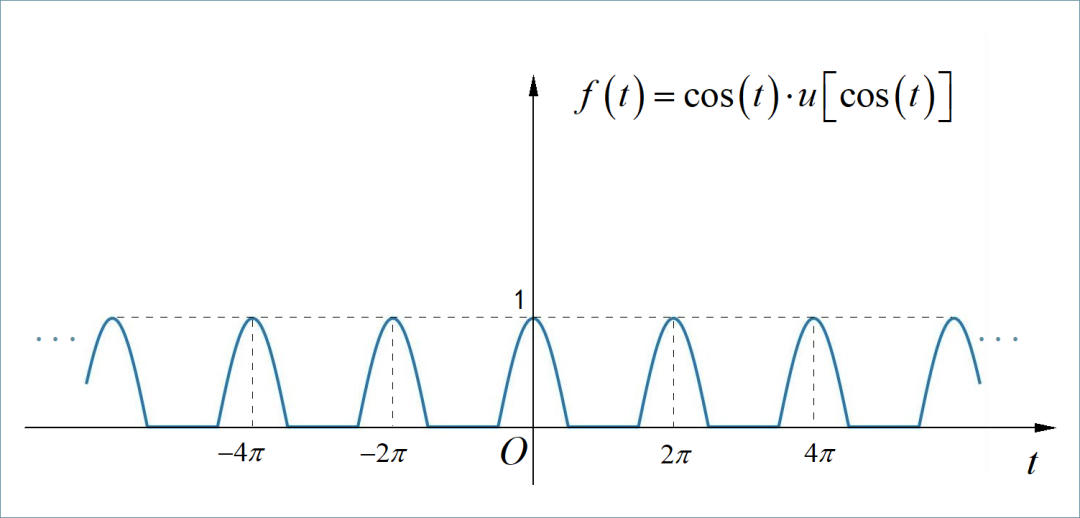
▲ 图2.1 半波整流信号□ 解答:

(3) 非周期信号
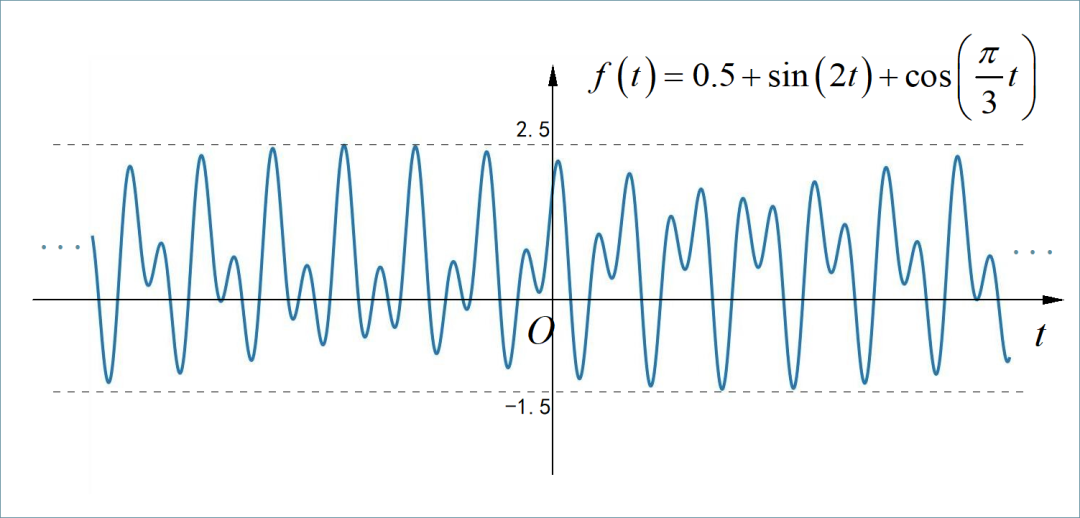
▲ 图2.2 非周期信号□ 解答:
这是一个非周期信号,根据信号的表达式可以判断出:
(4) 交错矩形信号
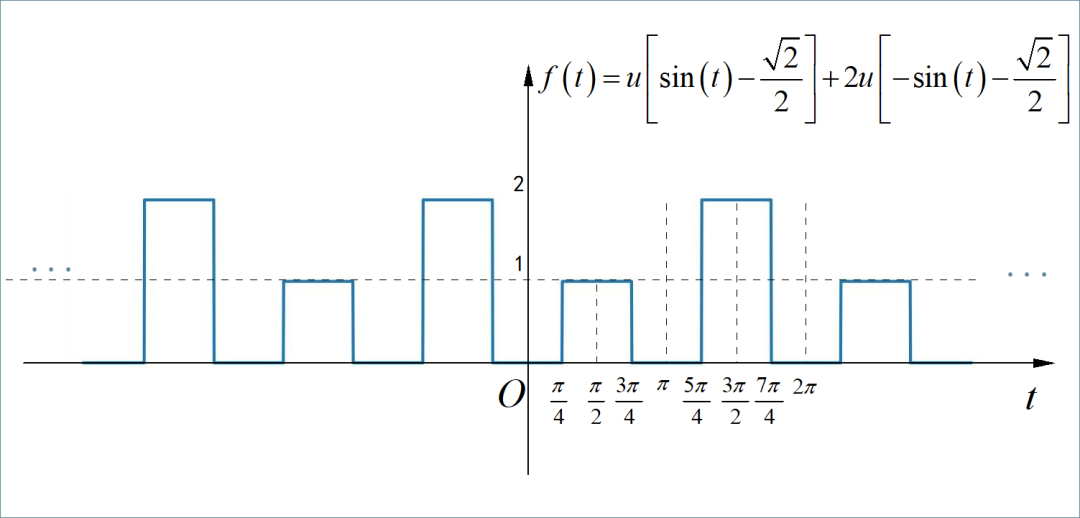
▲ 图1.1.4 交错矩形脉冲信号□ 解答:
(1) 奇偶分解
分别绘制出下面有现场信号的的积分量和偶分量。
□ 第一小题解答:

▲ 图1.2.1 连续时间信号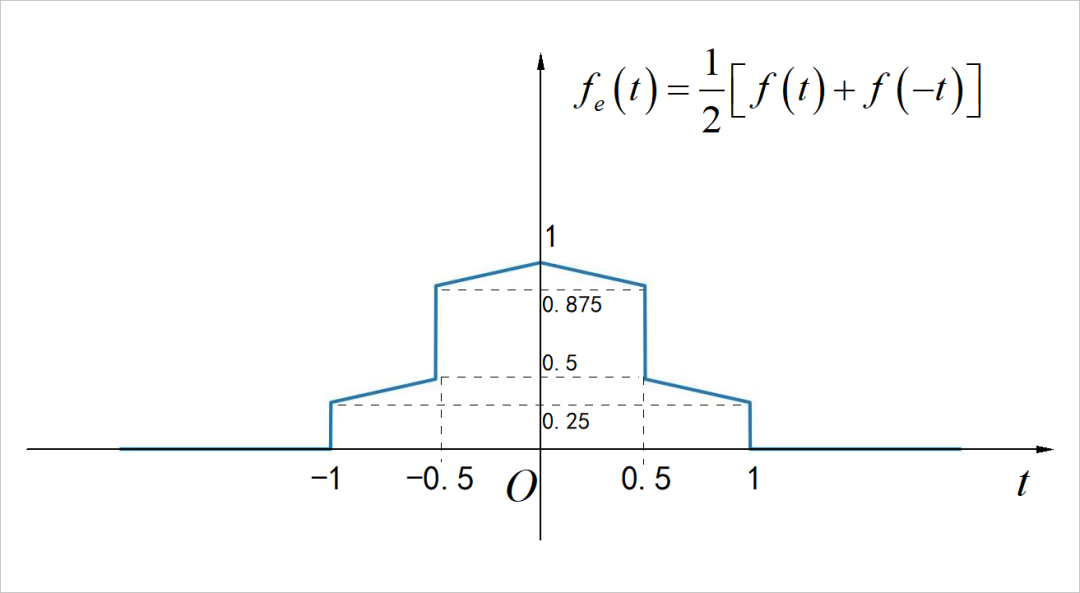
▲ 图2.3 信号的偶分量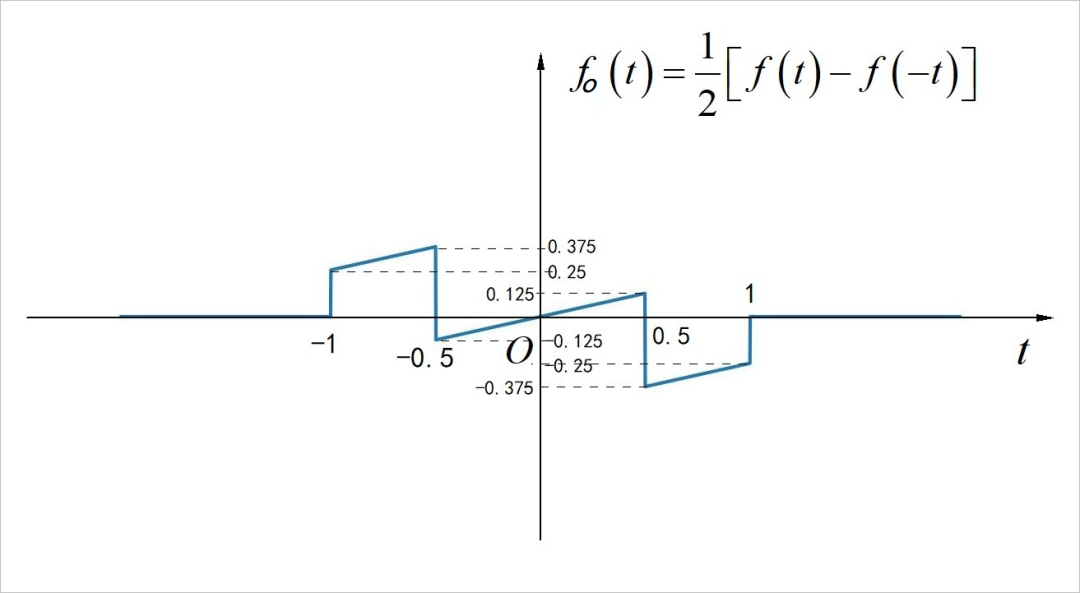
▲ 图2.3 信号的奇分量□ 第二小题解答:
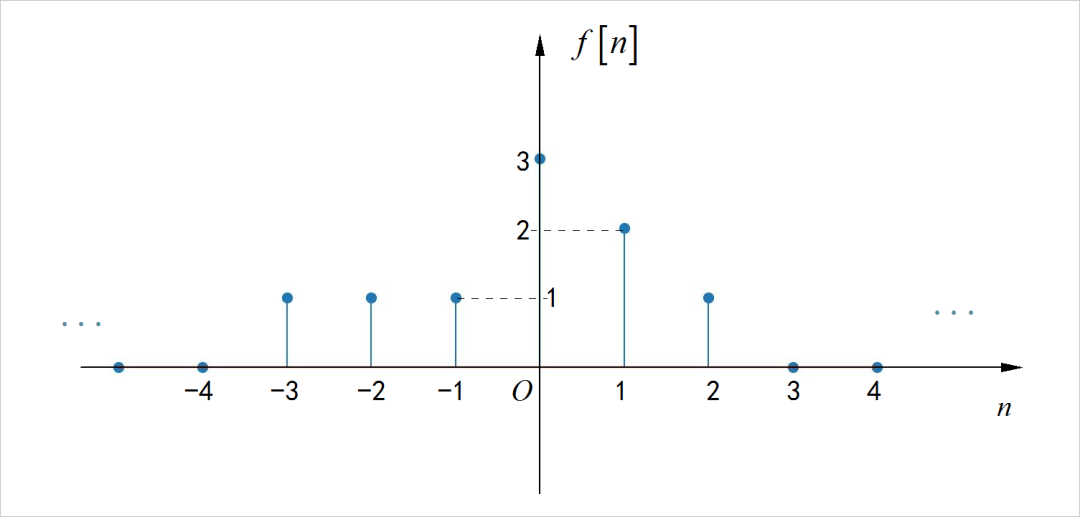
▲ 图1.2.2 离散序列信号
▲ 图2.5 信号的偶分量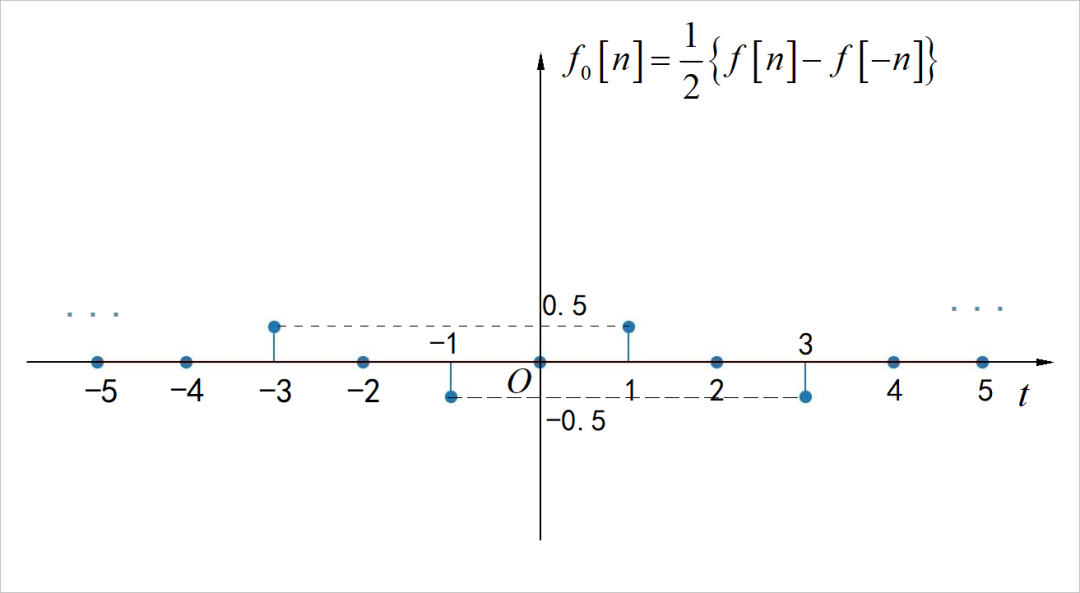
▲ 图2.6 信号的奇分量(2) 求解原信号波形
根据已知的信号 偶分量与左半边波形,绘制出原始信号 的波形。

▲ 图1.2.3 信号的偶分量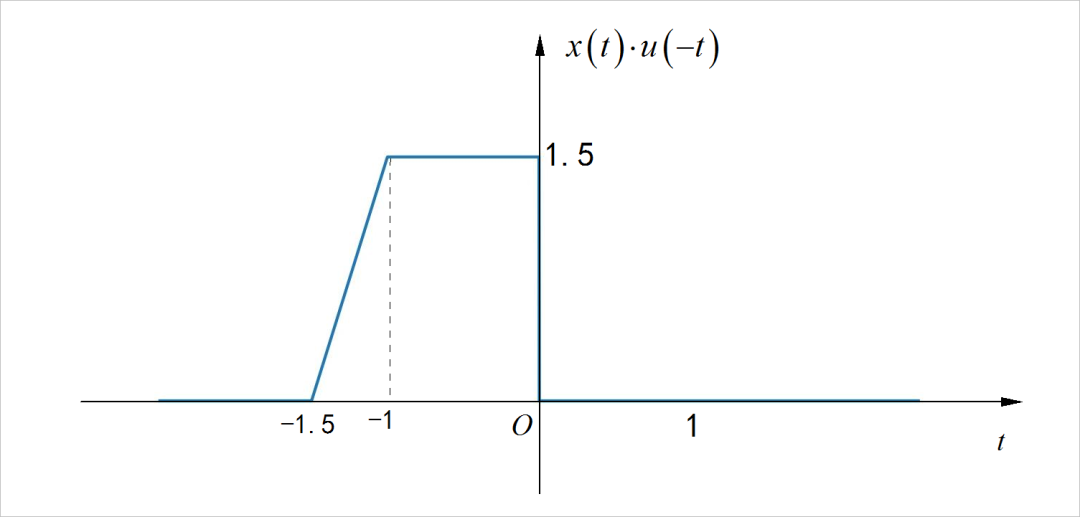
▲ 图1.2.4 信号的左半边部分□ 求解
根据已知信号的偶分量 以及信号左边信号,可以求出信号奇分量的左边部分:
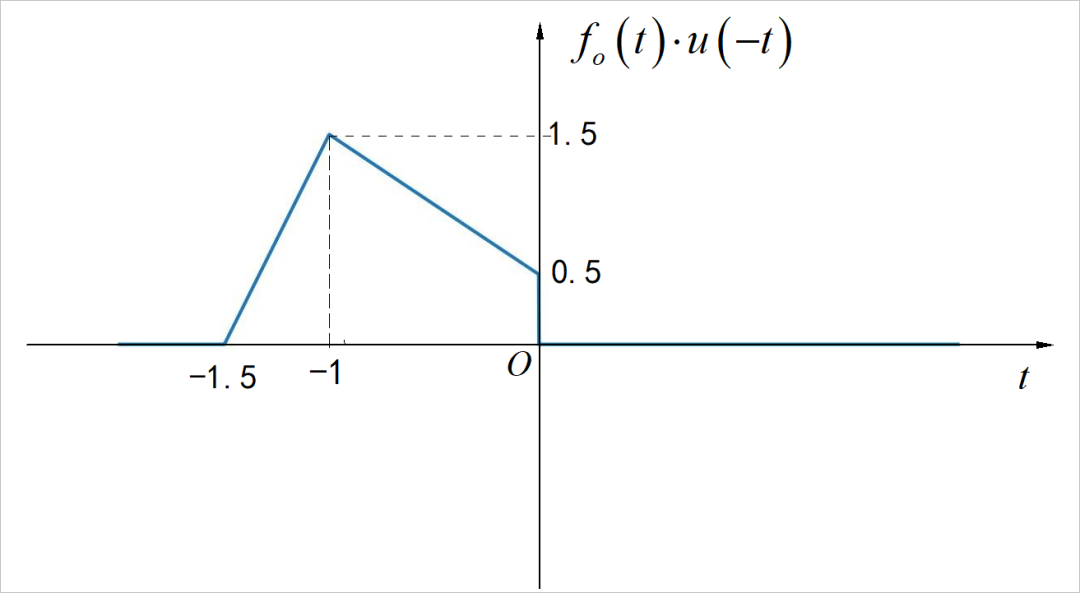
▲ 图2.9 信号的奇分量左半部分根据奇分量的对称性,可以绘制出全部奇分量的波形:

▲ 图2.10 信号的奇分量将偶分量加上奇分量,便可以得到信号波形。

▲ 图2.11 信号的波形(1) 信号奇偶分解
绘制出下面连续时间信号与离散序列的积分量和偶分量。
□ 第一小题解答:

▲ 图1.2.5 连续时间信号
▲ 图2.13 信号的偶分量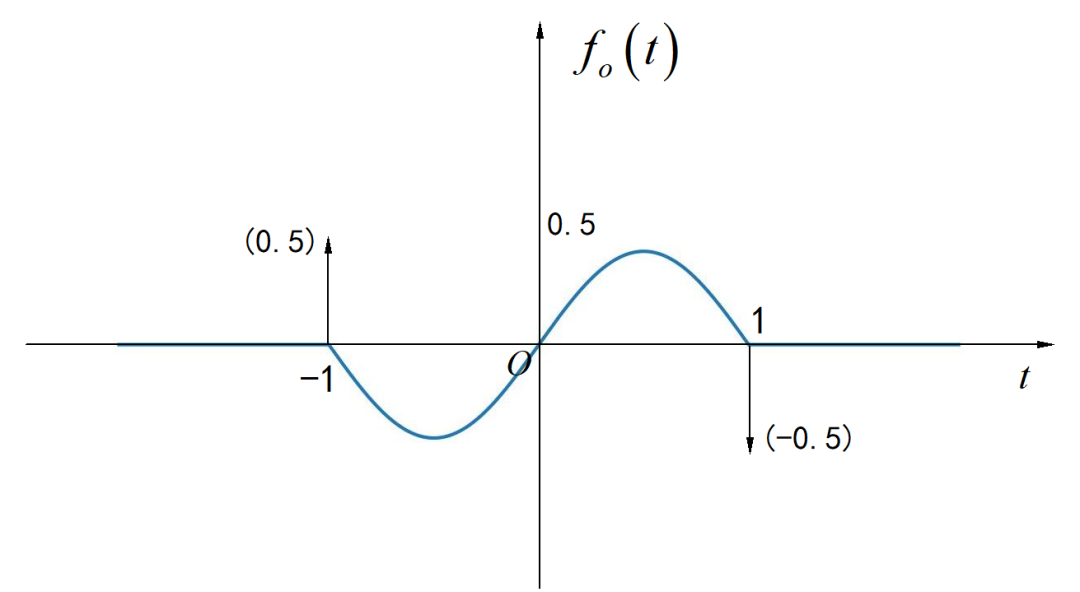
▲ 图2.14 信号的奇分量□ 第二小题解答:
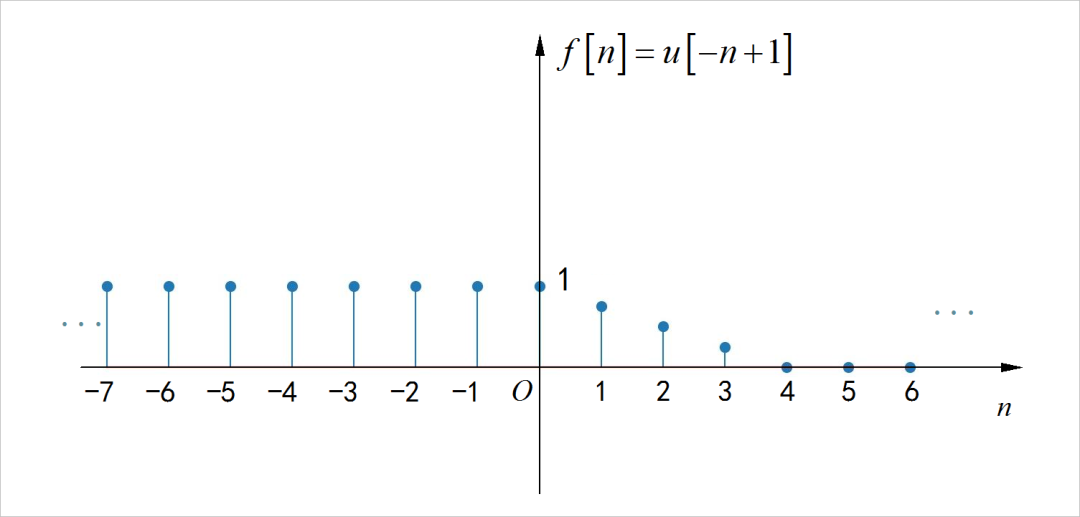
▲ 图1.2.6 离散时间序列信号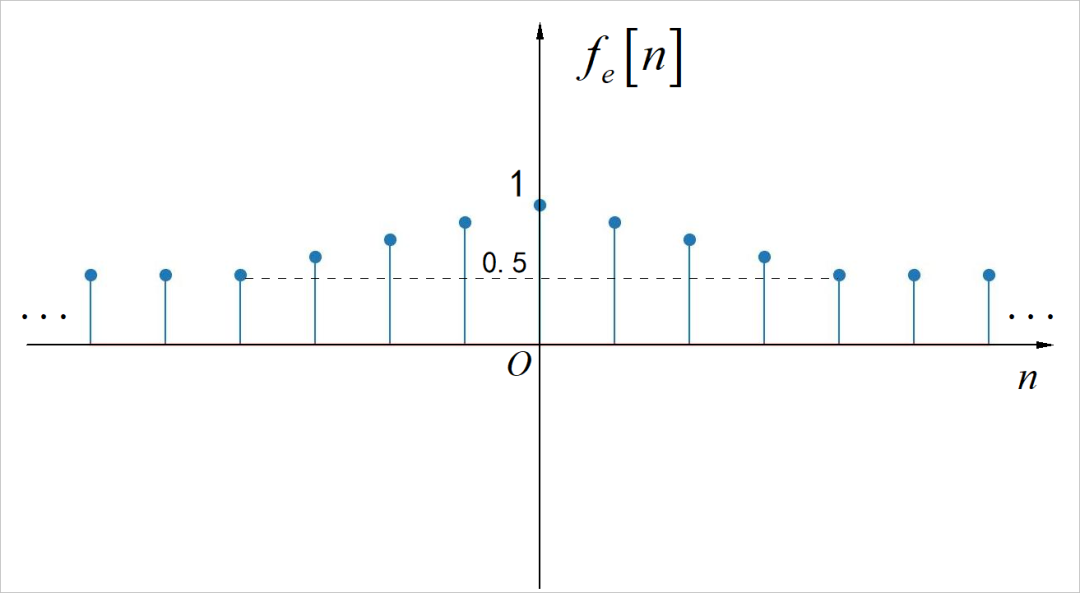
▲ 图2.16 信号的偶分量
▲ 图2.17 信号的奇分量已知连续时间信号 以及离散序列信号 的波形如下图所示,请根据表达式绘制出对应自变量变化后的信号波形。
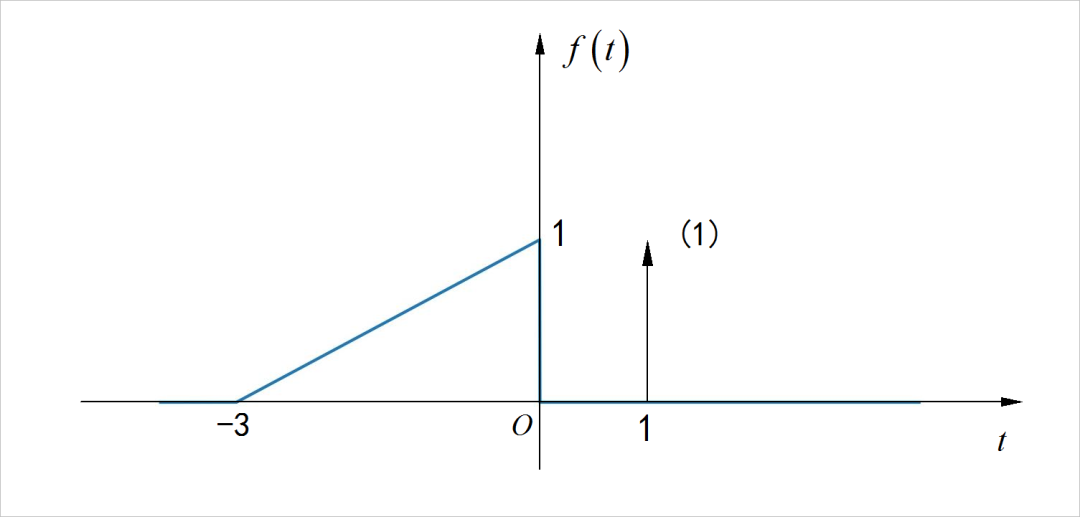
▲ 图1.3.1 连续时间信号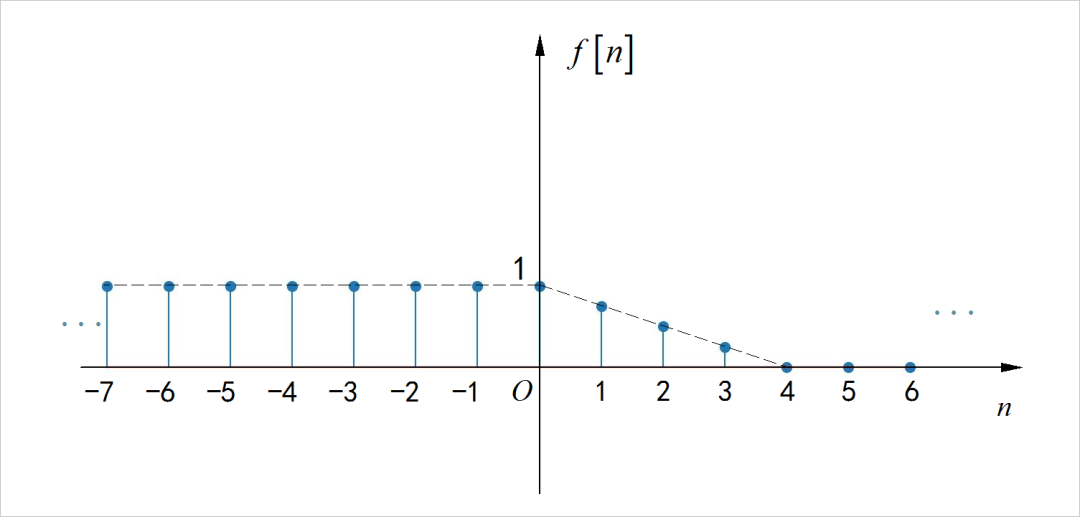
▲ 图1.3.2 离散时间序列(1)
□ 解答:
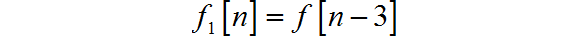
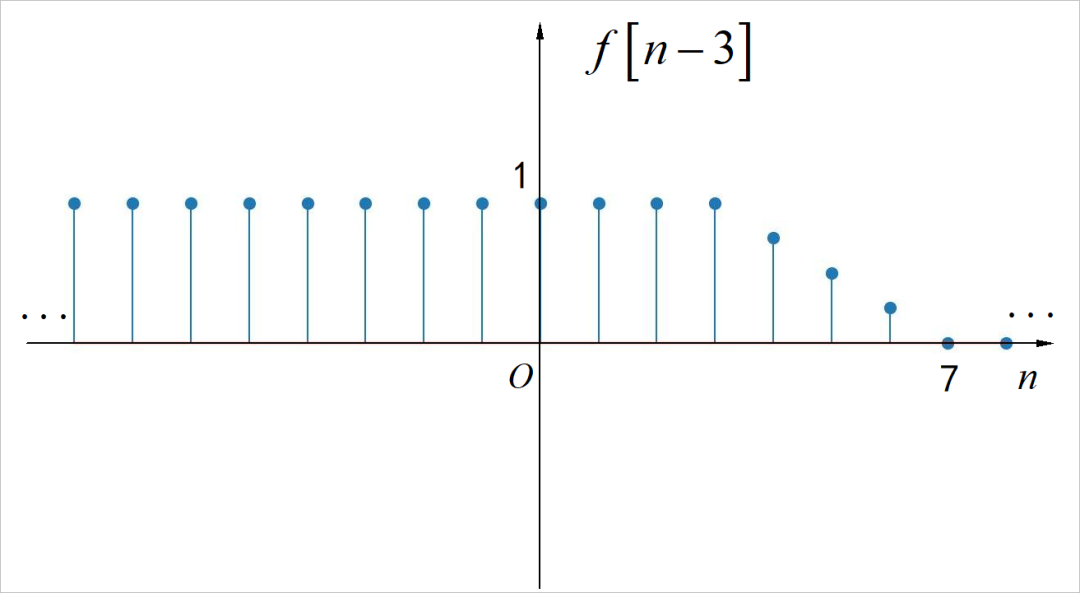
(2)
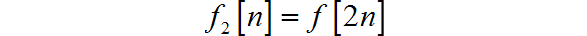
□ 解答:
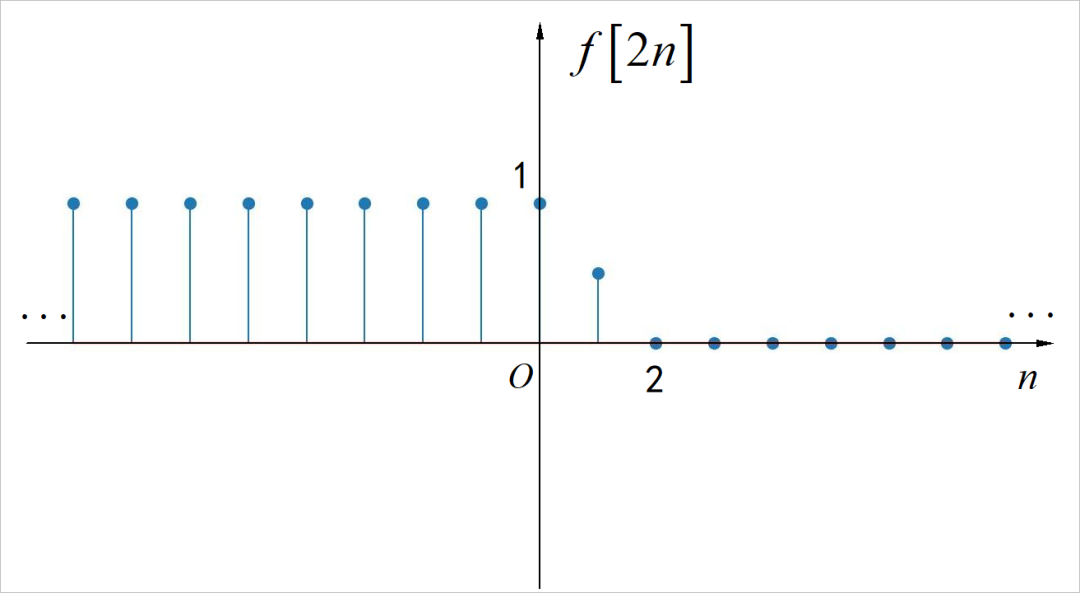
(3)
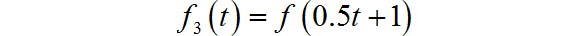
■ 求解:
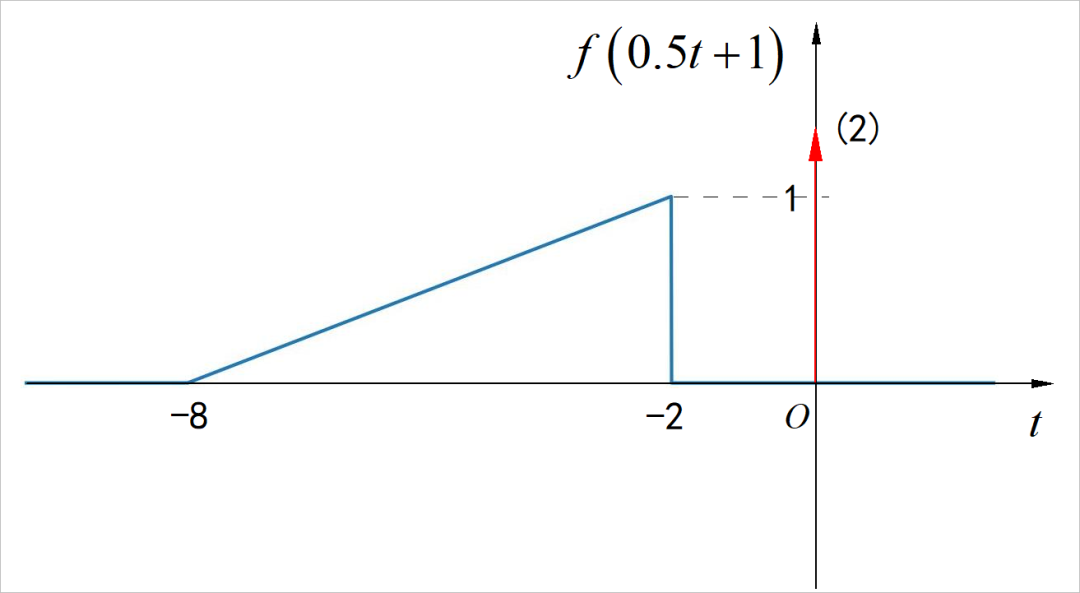
(4)
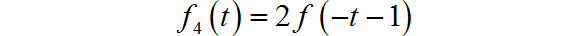 □ 解答:
□ 解答:

(1) □ 解答:
□ 解答:

(2)
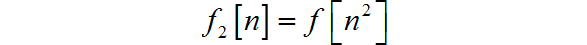 □ 解答:
□ 解答:
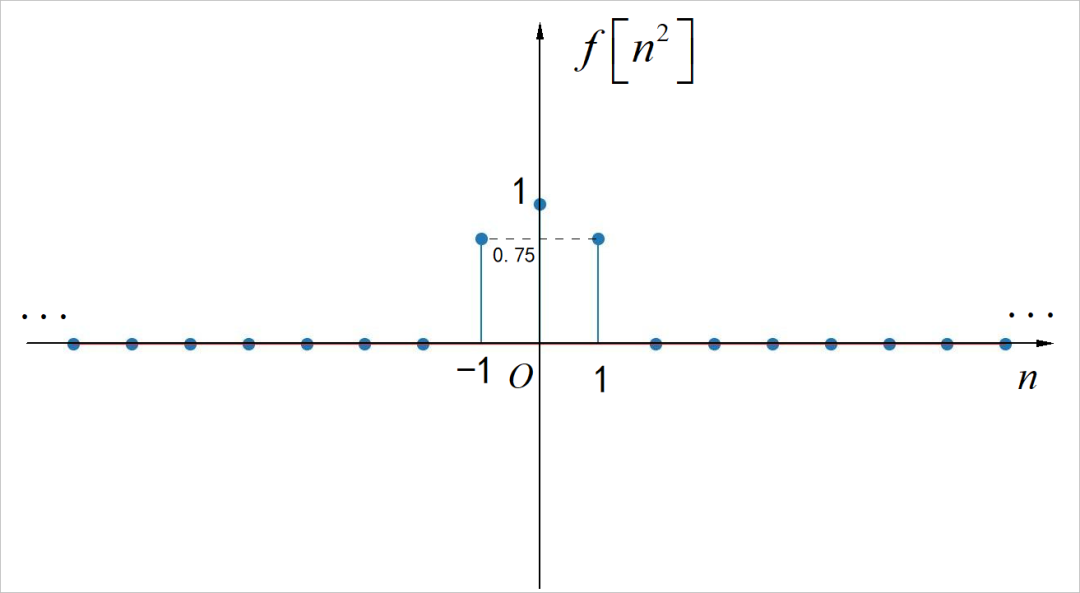
(3)

□ 解答:
由于自变量需要开方,所以要求 。信号的波形如下图所示:
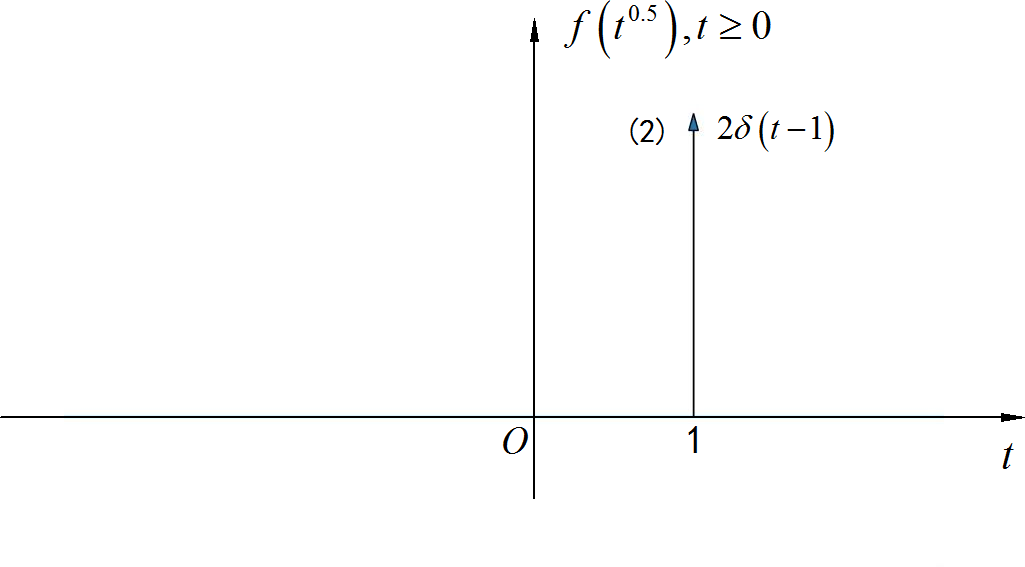
这里需要应用到 函数复合函数的特性: $$\delta \left[f\left( t \right)} \right] = \sum\limits_k^{} {{1 \over {\left\right)} \right|}}\delta \left( {t - t_k } \right)}$$ 其中 是函数 的零点。
(4)

□ 解答:
这个题目,实际上是必做题 第三小题的结果与 的乘积。可以看到最终的结果应该是 。所以函数为:

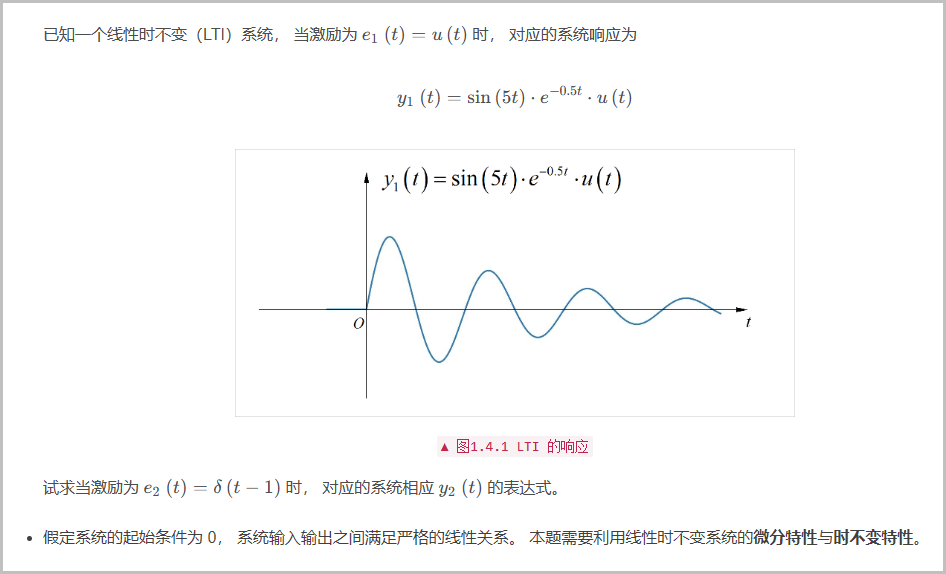 □ 解答:
□ 解答:
根据 LTI的微分特性,在 的作用下,系统的输出
因此,在 作用的系统输出

▲ 图4.1 输出波形的示意图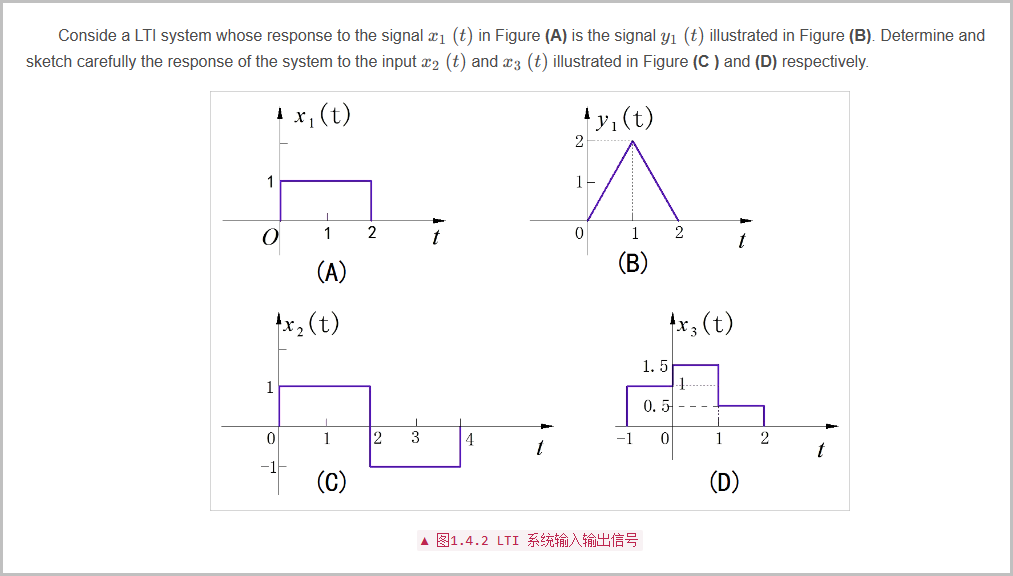
□ 解答:
对于信号 可以由 表示成:
所以对应的输出对应的信号波形为:
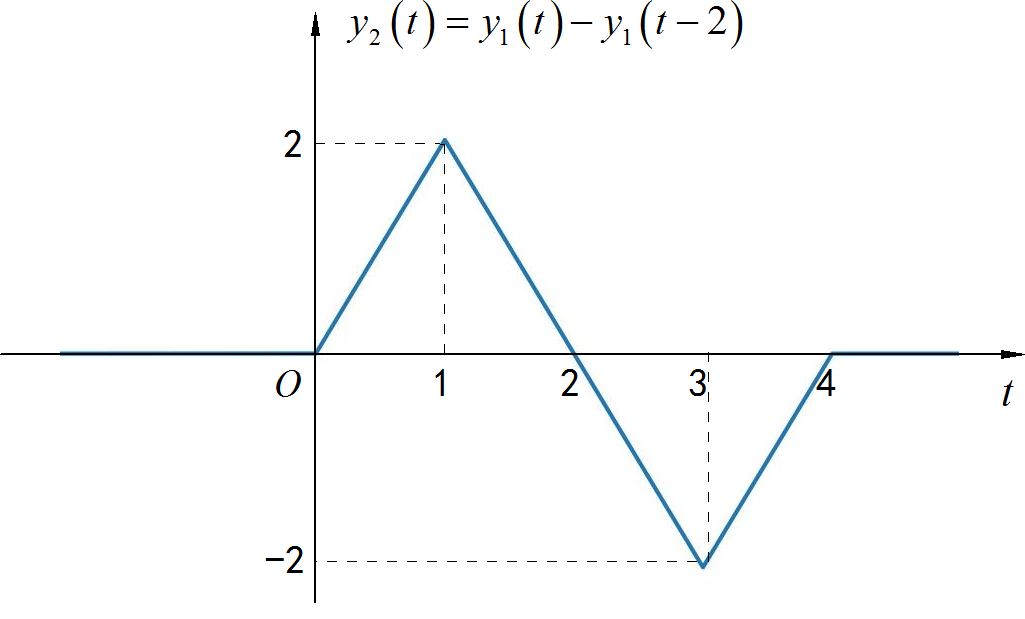
▲ 图1.4.2 信号波形对于信号 可以由 表示成:
那么对应的系统输出对应的信号波形:

▲ 图1.4.3 信号波形判断下列系统是否可逆。如果可逆则给出对应的逆系统。如果不可逆,则给出两个不同的输入信号,他们所引起系统的输出是相同的。
题目中,输入信号为 ,输出信号为 。
(1)
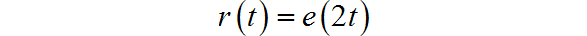
(2)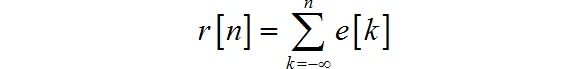
(3)
(4)
□ 解答:
(1) 系统可逆,逆系统为:
(2) 系统可逆,逆系统为:
(3) 系统可逆,逆系统为:
(4) 系统可逆,逆系统为:
讨论下面电路输入输出之间是陈本可逆?
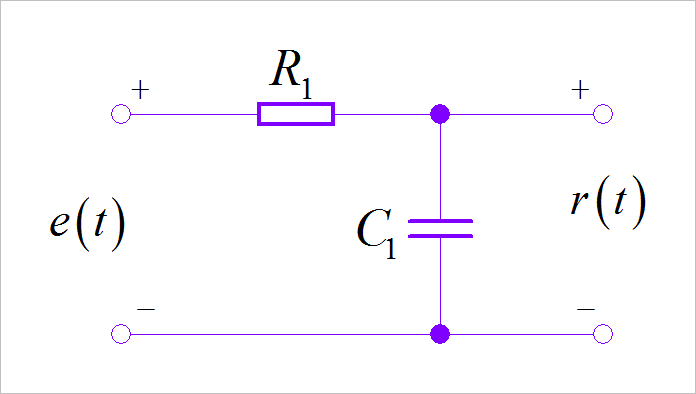
▲ 图1.5.1 低通滤波电路□ 解答:
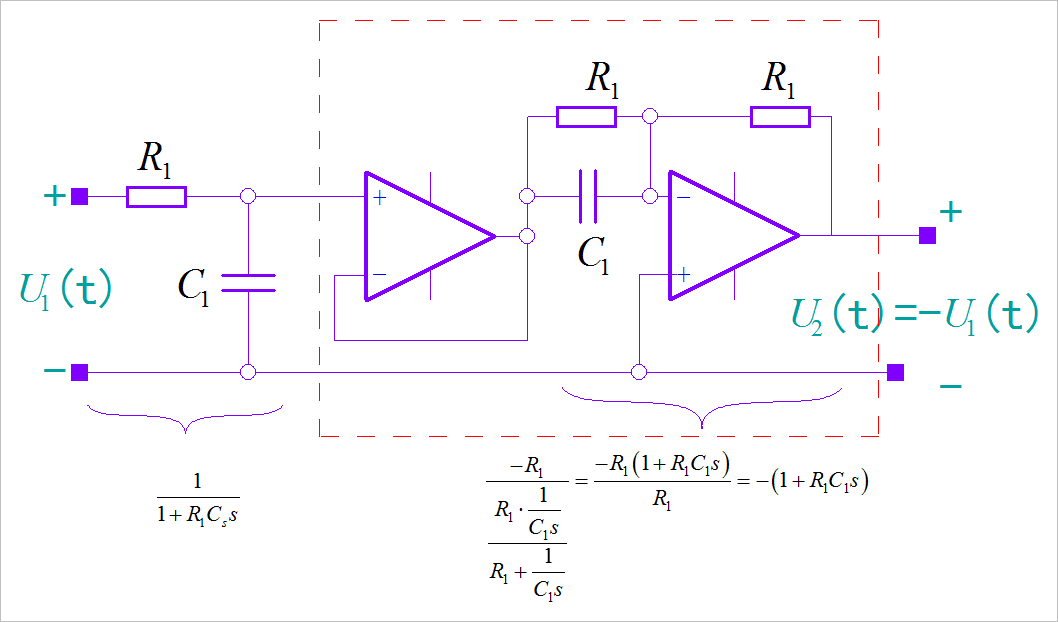
▲ 图1.6.1 RC低通滤波器的逆系统注意,上述电路最后还需要再经过一级的反向,才真正实现将原始信号进行恢复。
参考文献: Inverse Analog Filter:History, Progress and Unresolved Issues[4]
相关讨论: Low Pass Filter Inverse[5]
根据下面表格描述系统的输入输出关系表达式,分别判断系统的线性、时不变、因果 特性。
□ 解答:
| 序号 | 系统输入输出关系 | 线性? | 时不变? | 因果? |
|---|---|---|---|---|
| 1 | 线性 | 时不变 | 因果 | |
| 2 | 线性 | 时变 | 因果 | |
| 3 | 线性 | 时变 | 非因果 | |
| 4 | 线性 | 时变 | 非因果 | |
| 5 | 非线性 | 时不变 | 因果 | |
| 6 | 线性 | 时变 | 因果 | |
| 7 | 线性 | 时变 | 非因果 |
试写出下面各图对应的系统输入输出之间的微分方程和差分方程。请大家注意本题中采用了不同的符号表示了积分、延迟,请大家注意辨识这些不同的表示方法。
本次作业中有一些框图与 信号与系统 2022 春季学期第二次作业[6] 中具有相同的结构,但是相关系数进行了改变,请大家注意区分。
□ 第一小题解答:
(1)

▲ LTI系统框图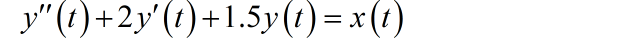
□ 第二小题解答:
(2)
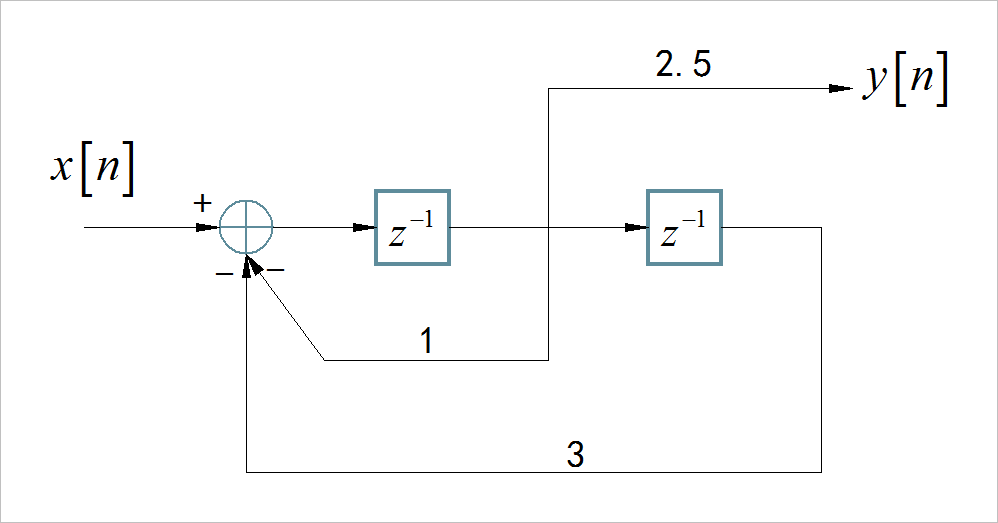
▲ 图1.7.2 离散时间系统框图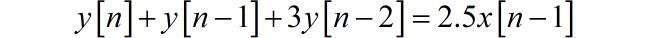
□ 第三小题解答:
(3)
在系统狂种种见增加临时变量 ,
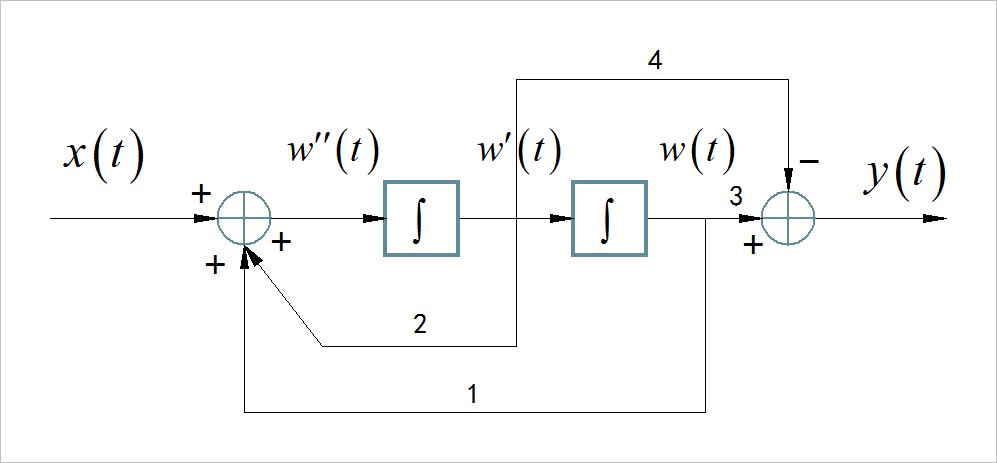
▲ 图7.3 增加有临时变量的系统框图根据两个综合器,分别列写出两个微分方程:

使用算子方法,对微分方程进行化简。使用 D 作为微分算子,上面两个方程转换成算子方程:

因此:
 最终,系统对应的微分方程为:
最终,系统对应的微分方程为:
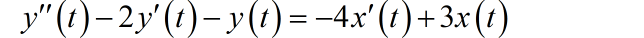
□ 第四小题解答:
(4)
在系统框图中增加中间临时变量。
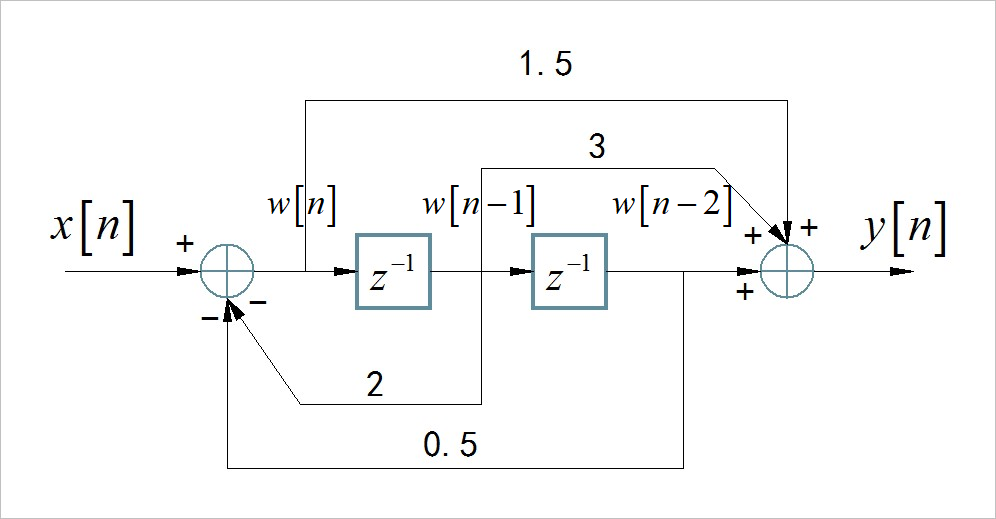
▲ 图7.4 增加有中间变量的系统框图根据两个综合器,列写出两个差分方程:
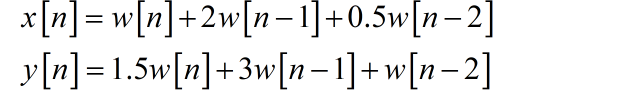
仿照前面使用算子方法,消去中间变量。这里省略了中间的步骤,给出最终的差分方程:
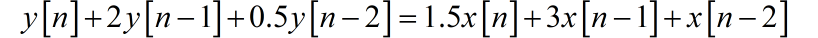
□ 第一小题解答:
(1)
给系统框图增加两个中间变量。
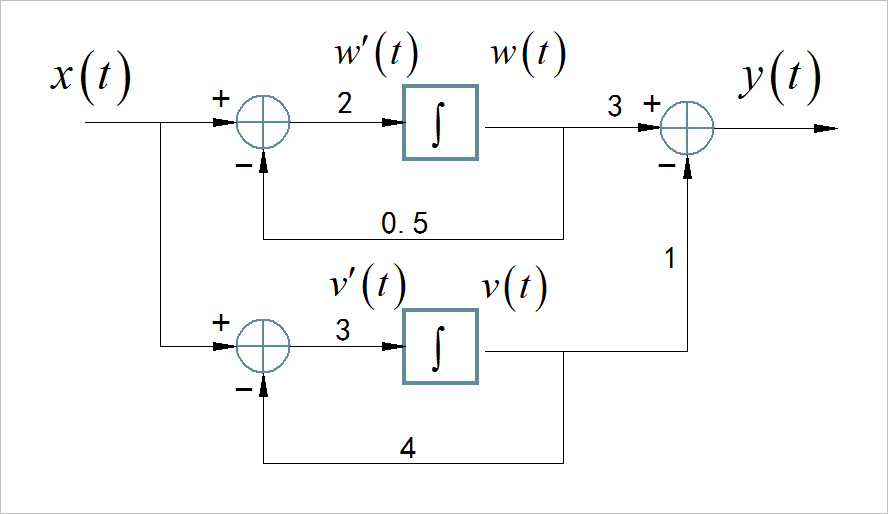
▲ 图7.5 增加有中间变量的系统框图列写出微分方程:
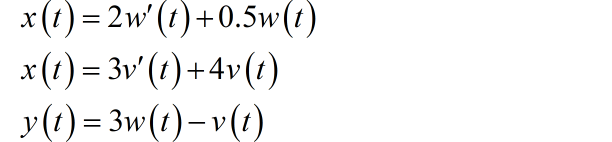
还是使用微分算子方法,化简上述微分方程组,可以得到:

最终可以得到系统的微分方程:

□ 第二小题解答:
(2)
给系统增加一个中间变量:

▲ 图7.6 增加有中间变量的系统框图根据最上面的两个综合器,列写出两个差分方程:
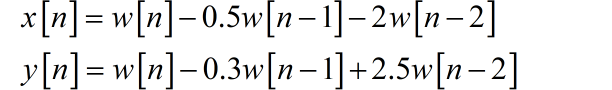
同样使用延迟算子方法,消去中间变量,下面给出最终的差分方程:

信号与系统2024(春季)作业要求以及参考答案汇总: https://zhuoqing.blog.csdn.net/article/details/136798840
[2]信号与系统2024(春季)作业要求 - 第二次作业: https://zhuoqing.blog.csdn.net/article/details/136533172
[3]RC低通滤波器的逆系统: https://zhuoqing.blog.csdn.net/article/details/124342292
[4]Inverse Analog Filter:History, Progress and Unresolved Issues: https://www.mdpi.com/2079-9292/11/6/841/pdf
[5]Low Pass Filter Inverse: https://electronics.stackexchange.com/questions/273756/low-pass-filter-inverse
[6]信号与系统 2022 春季学期第二次作业: https://zhuoqing.blog.csdn.net/article/details/123258268