
(1) 微分方程求解
已知 LTI 系统输入输出之间的微分方程如下:
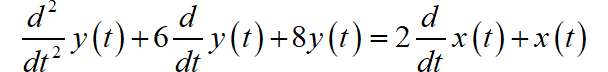
输入信号为:
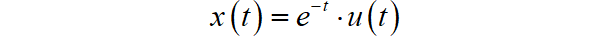
系统的起始状态为:
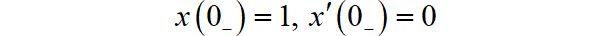
分别求出:
(1) 系统的完全响应;
(2) 指出响应中的自由响应、强迫响应、瞬态响应、稳态响应、零输入响应、零状态响应各个分量;
(3) 求解该系统的单位冲激响应,单位阶跃响应。
提示: (1)根据奇异函数匹配 方法求出系统 时刻的处处条件求解完全响应中待定系数; (2)自行验证第三小题中单位冲击相应与单位阶跃响应之间的微分关系;
(2) 差分方程求解
已知离散时间系统对应的二阶后向差分方程如下:
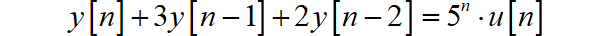
初始条件为:
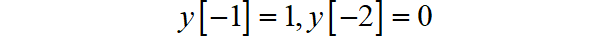
分别求出:
(1) 该系统的完全响应;
(2) 分别指出系统的自由响应、强迫响应、瞬态相应、稳态响应;
(3) 求出系统的零输入响应、零状态响应。
(1)求解系统的单位冲激响应
已知 LTI系统对应的微分方程为:
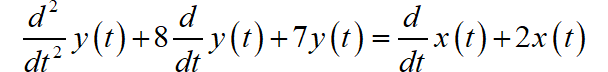
求解该系统的单位冲激响应。
(2) 求系统的单位冲激响应
已知 LTI 系统的输入输出之间对应的微分方程为:
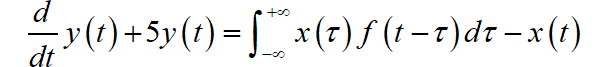
其中: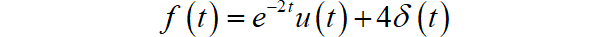
求该系统的单位冲激响应: 。
提示: 上面方程右边包括有系统的输入信号 与 的卷积以及 部分。根据单位冲激响应的定义,把 代入方程右边之后便可以得到关于输出信号的微分方程,求解之后便可以得到系统的单位冲激响应。
(1)电路系统
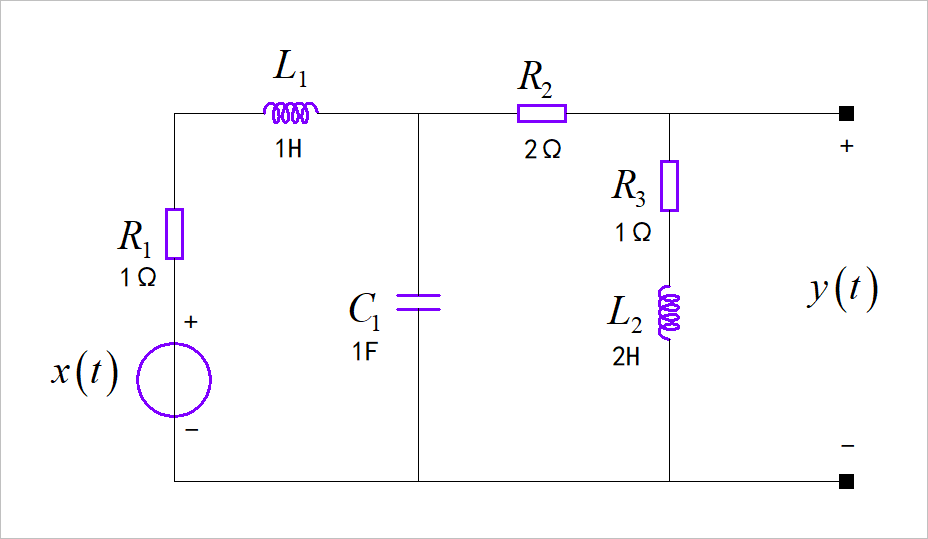
▲ 图1.1.1 RLC电路(2) 液体混合
在某一容器中对 A、B 两种液体进行混合。在第 步,把 升液体 A 和 升液体 B 都导入容器中,假设 。该容器已有 900 升 A 与 B 的混合液。均匀混合后,再从容器中倒出 100 升混合液。如此重复上述过程在第 个循环结束后,假设 A 在混合液所占百分比为 。
(1) 试列写出 , 之间的差分方程;
(2) 如果已知 , ,求解 ;
(3) 指出其中的自由分量和强迫分量;
(4) 当 时,
注意: 这个题目中,混合溶液的体积以及 的变化与去年作业有所区别。
(1) 带有互感的电路
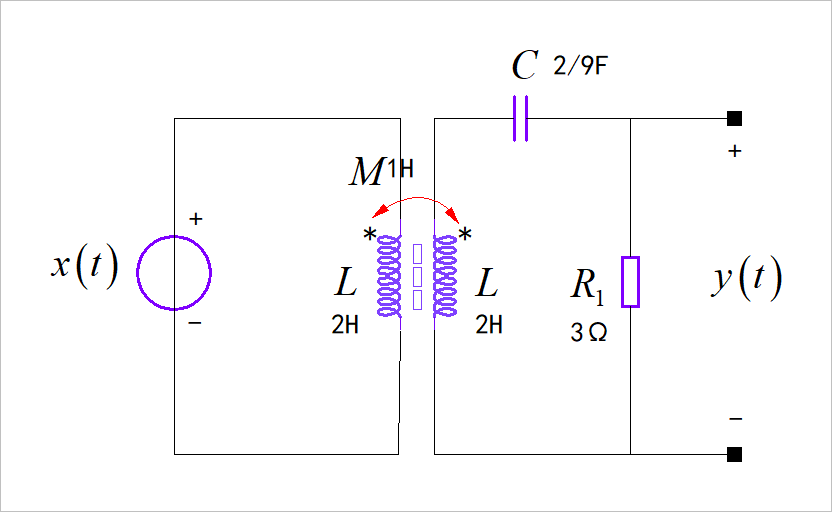
▲ 图1.1.2 带有互感的电路(2)双音频电路差分方程
在电话拨号中,使用了双音频信号对按键进行编码。比如下面序列对应着两个频率信号叠加后采样后的序列, 。采用频率为 ,对应采样间隔为 。
在设计一个双音频信号芯片中,希望通过迭代方式产生下面双音频序列。请写出下面双音频序列对应的差分方程,以及对应的起始条件。 。
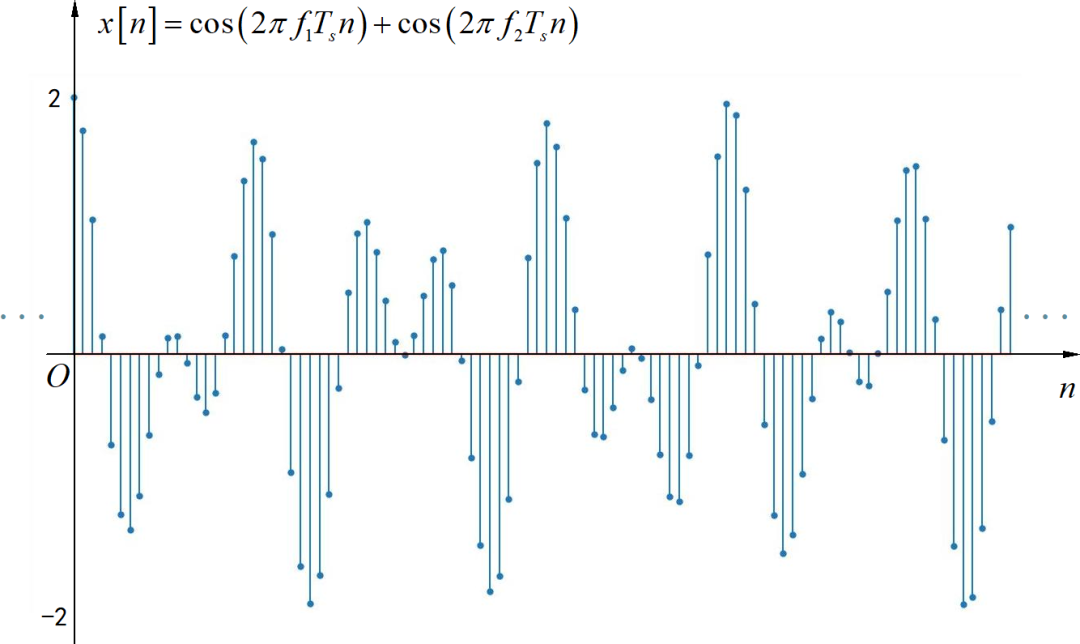
▲ 图1.1.3 双音频信号序列有一系统在激励信号为 时完全响应为:
当激励变为: 时完全响应为:。(1) 求该系统的零输入响应的: ;
(2) 系统的其实状态不变,求其对激励为 时的完全响应
提示: 求解第一问:将完全响应分解成对应的零输入响应和零状态响应。在两次输入信号下分别为 作用下,对应的零输入相应的分量 保持不变;而两次零状态响应 之间满足微分关系: $r_{zs1} \primeleft( t \right) = r_{zs2} \left( t \right)$r_1 \left( t \right) = r_{zi} \left( t \right) + r_{zs1} \left( t \right) = 2e{ - t} u\left( t \right)
r_2 \left( t \right) = r_{zi} \left( t \right) + r_{zs2} \left( t \right) = r_{zi} \left( t \right) + r'_{zs1} \left( t \right) = \delta \left( t \right)$$将上面两个等式相减便可以得到关于 的微分方程,求解该微分方程得到 之后,便可以得到。 。
求解第二问时,可以先根据第二次输入 时的结果求出系统的单位冲激响应的 。然后在利用卷积计算出输入信号为 时的零状态响应,加上系统的零输入响应 便可以得到系统的完全输出了。
如果已知系统的输入输出关系可以使用二阶常系数差分方程来描述。在输入信号为
时对应的系统响应为:$$y\left[ n \right] = \left[ {2n 3 \times 5n 10} \right] \cdot u\left[ n \right]$$(1) 如果系统起始为静止的,也就是零状态(满足松弛条件),试确定该系统的二阶差分方程;
(2) 如果激励为:
求系统的响应: 。这次实验是针对一款由运放搭建的放大滤波电路进行建模分析。实验目的:
实验作业是选做题,大家可以根据自己的时间安排以及经验,选择合适的软件工具对电路进行分析。
2020年的新冠疫情使得很多人被迫留在了家里。今日头条在2020年9月份有一篇博文: 在家做核子研究:怎么DIY一个粒子检测器[3] 记录了博主Steve Foster 和他的16岁儿子关在家里,鼓捣着 DIY 一个粒子探测器,这是他在网上碰巧看到了一篇介绍欧洲核子研究中心(CERN)外联项目的文章,这个项目说,你能以不到30英镑的价格打造你自己的粒子探测器?
之所以能够使用很便宜的方法来探测放射性粒子,主要得益于可以使用PIN光电管来代替盖革管检测高能光子所产生的电离放电脉冲电流。

▲ 图2.1 用于检测放射性粒子的两款PIN光电管在博文 怎么DIY一个粒子检测器[4] 介绍了他制作放射粒子检测器所使用的传感器和相关电路。下图便是检测电路的原理图。
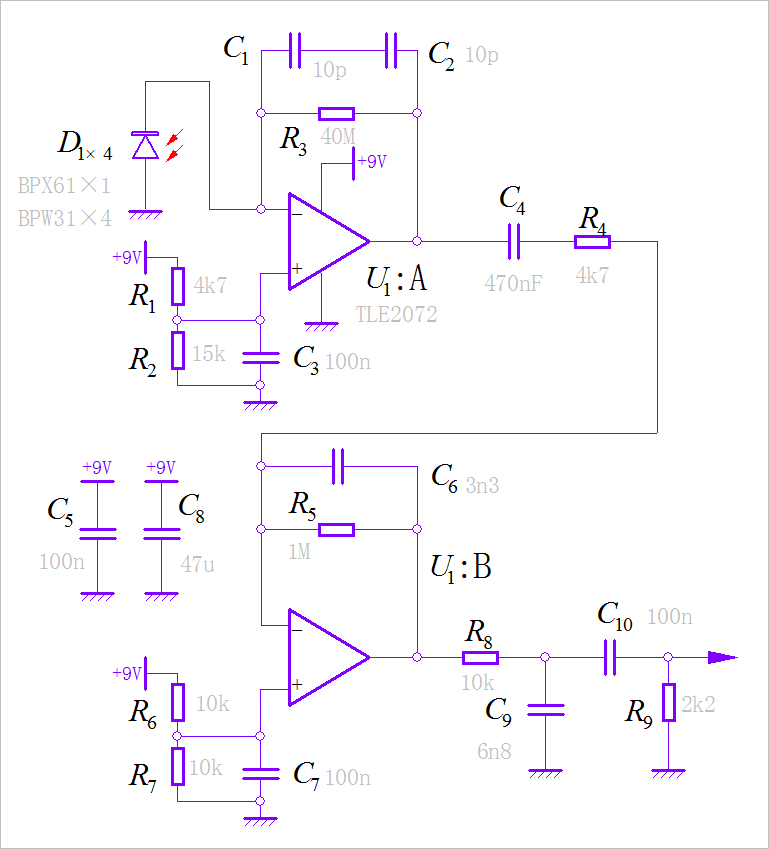
▲ 图2.2 对放射性粒子电流进行放大的电路原理图由于放射性粒子在PIN光电管所产生的电流非常短促,可以近似看成一个冲击电流: 。其中 反映了粒子不同的能量所产生冲激电流的强度。
对于每一个放射性粒子所产生的电流,电路放大后输出的信号反映了该电路的单位冲击相应信号 。下图便是“Steve Foster” DIY的粒子探测器所记录的放射脉冲信号。
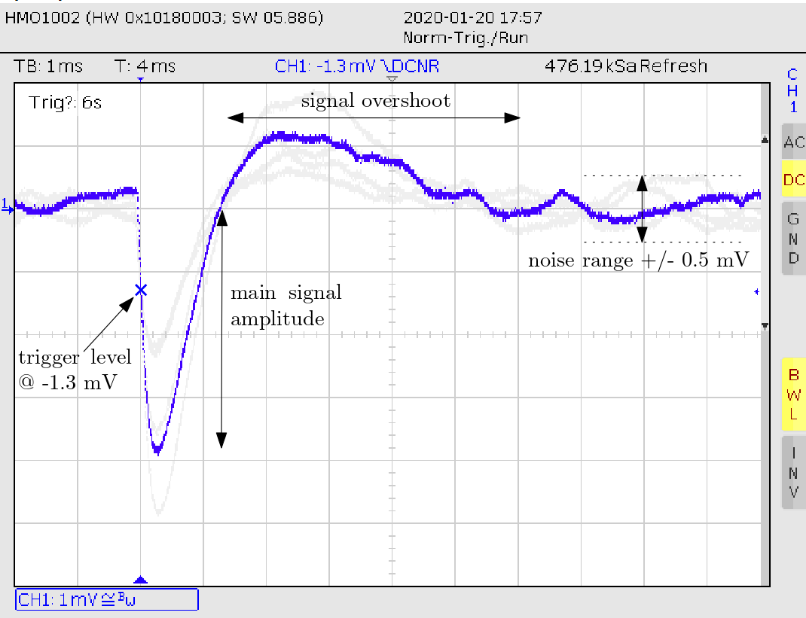
▲ 图2.1.3 记录到α粒子电路输出脉冲信号通过统计信号的峰值可以获得放射性粒子能量谱分布,进而可以对放射源特性进行进一步分析。
根据【图2.2】电路图,请建立电路输入端,即光电管D 到电路输出端电阻 上电压之间的微分方程。求解该电路系统的单位冲击响应,对比【图2.1.3】实测的脉冲信号,看他们是否波形上是出相符的。
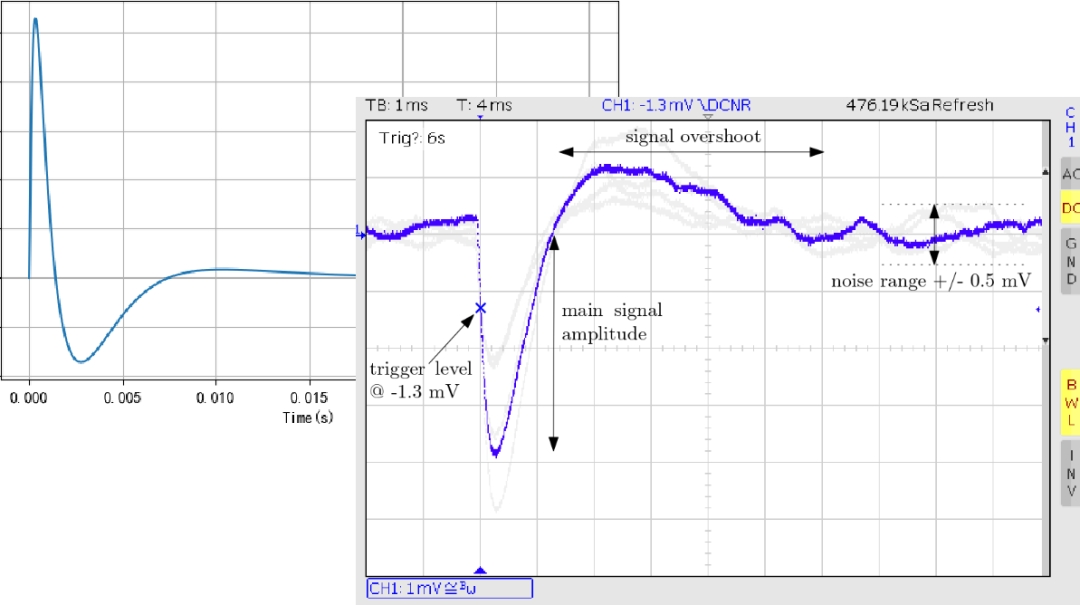
▲ 图2.2.1 电路求解仿真的波形与实际测量波形对比大家可以根据自己所熟悉的电路仿真工具和软件来完成电路的单位冲激响应信号的分析。比如可以选择:
在博文 滤波器电路的Python仿真[5] 给出了利用Python求解该粒子放大电路的分析过程。大家可以参照进行学习和求解。
对于上述复杂动态电路系统,使用s域分析方法可以方便得到输入输出之间的转移函数,由此可以进一步获得输入输出之间的微分方程。下面是博文中利用Python中的符号推导软件获得输入输出之间的转移函数。利用系统仿真工具便可以获得系统的单位冲激响应。
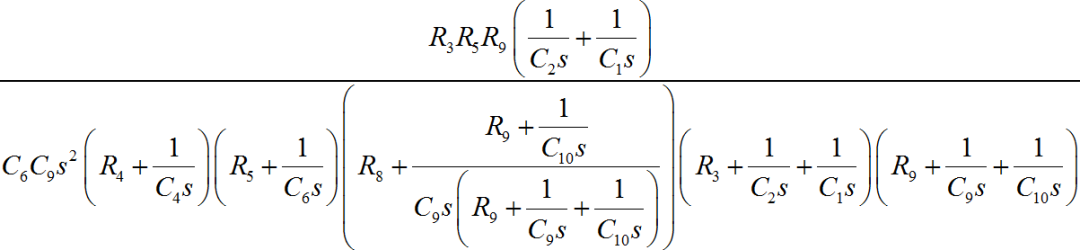
▲ 图2.3.1 在上述博文中给出的电路输入输出之间的S域的转移函数相应的Python编程可以参见上述博文。
信号与系统 2023(春季) 作业要求 - 第三次作业: https://zhuoqing.blog.csdn.net/article/details/129423119
[2]信号与系统 2022 春季学期第三次作业: https://zhuoqing.blog.csdn.net/article/details/123403423
[3]在家做核子研究:怎么DIY一个粒子检测器: https://www.toutiao.com/i6877045217581597191/?tt_from=weixin&utm_campaign=client_share&wxshare_count=1×tamp=1601268327&app=news_article&utm_source=weixin&utm_medium=toutiao_ios&use_new_style=1&req_id=2020092812452701013109907703B3DAE7&group_id=6877045217581597191
[4]怎么DIY一个粒子检测器: https://zhuoqing.blog.csdn.net/article/details/108854559
[5]滤波器电路的Python仿真: https://blog.csdn.net/zhuoqingjoking97298/article/details/108936689?ops_request_misc=%25257B%252522request%25255Fid%252522%25253A%252522160905372916780310129439%252522%25252C%252522scm%252522%25253A%25252220140713.130102334.pc%25255Fall.%252522%25257D&request_id=160905372916780310129439&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_v2~rank_v29_name-1-108936689.pc_search_result_no_baidu_js&utm_term=%E7%94%B5%E8%B7%AF%20%E4%BB%BF%E7%9C%9F%20%E5%8D%93%E6%99%B4