今年打算做2件事。
① 板级低噪放课程:
打算做板级低噪放设计课程,课程内容,打算是从原理图+版图仿真开始,然后画板,然后投产+调测。
价格的话是149元,如果前期报过系统课程的话,则优惠50元,为99元。
②芯片LNA共学营:
这个项目主打自己学习为主,外援老师教授为辅助。 报名的号友,都会在一个群里,学习主要是靠自学。我每天会花四个小时左右在芯片学习上。因此我会列出每周自己的学习计划,以及给出自己的学习心得。号友可以参考我的计划,也可以遵照自己的计划进行。中间,会请老师进行辅导和答疑,大概会进行三次左右。
共学营开营后,会设置一个流片的deadline(目前打算设置在一年左右),需要在这个deadline之前把版图准备好,大家一起流片。
价格是3999元。
你有意愿报名的话,可以加我微信,说明一下意向,并注明是对板级有兴趣,还是芯片级的有兴趣。
说明意向的时候,不用付费,等我差不多规划完,确认开班了,我再统一拉群。

(1)
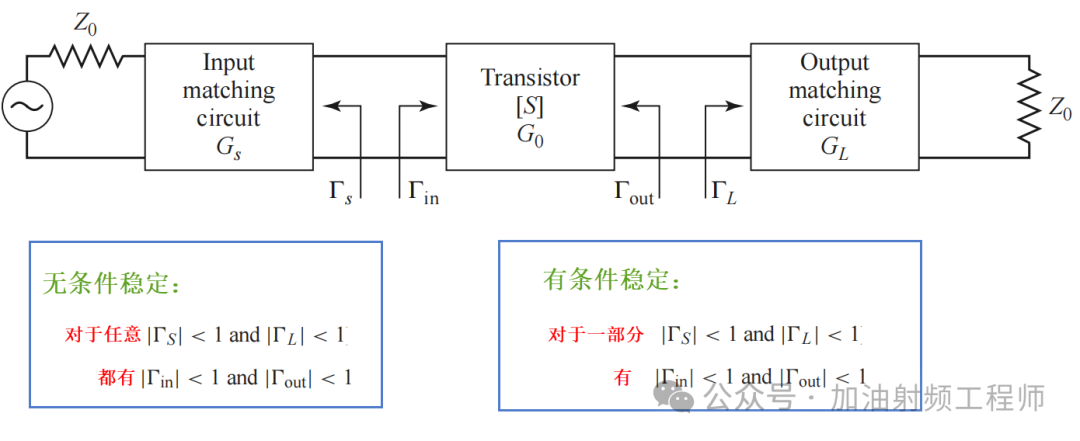
放大器有两种类型的稳定性,一种称为无条件稳定,一种称为有条件稳定。
所谓无条件稳定,就是不管放大器的源是多大,负载是多大,只要源和负载都是无源的,放大器都不会发生振荡。
所谓有条件稳定,就是只有放大器的源和负载,处在一个范围之内,放大器才不会发生振荡。
如果用图和公式来表示的话,可以如下图所示。
(2)
判别放大器是否是无条件稳定,在文献[1]中提到,有两种方法。
一种是K-△准则,即:
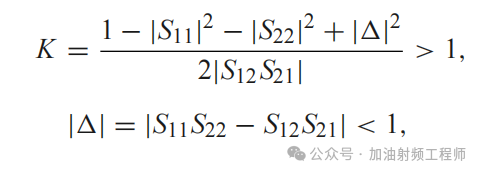
另外一种是u准则,即:
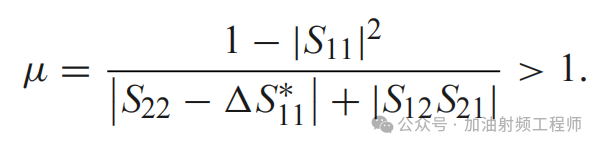
不过,在文献[2]中,还提到一个u'准则[2],如下图所示。
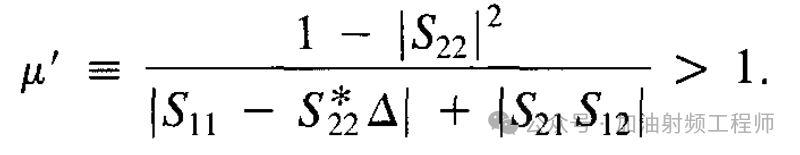
这个u'和u有点对偶的关系,一个是在ΓL平面,一个是在ΓS平面,而且两个准则,等价,即:
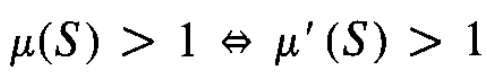
在文献[1]中,有这样一段话:

也就是说,因为K-△准则,包含两个判别式,所以不能用来比较两个器件之间的稳定程度;但是u可以,u越大,意味着稳定性越大。
(3)
所以,为啥u越大,意味着稳定性越大呢?
首先来看一下u的定义。
文献[2]中提到:

也就是说,u不仅仅是一个公式,它具有物理意义,表示的是在ΓL平面内,SMITH圆图的原点与不稳定区域之间的最短距离。
比如说,在[1]的Example12.2中,有:

计算出来的u值为:
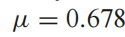
计算出来的输出稳定圆(Output stability circle),如下图所示。其中绿箭头所示的长度,为|CL|-RL=0.675,和上述计算出来的0.678基本一致。
也就是说,这个计算验证了上述的说法。即u表示的是SMITH圆图上的原点与不稳定区域之间的最短距离。
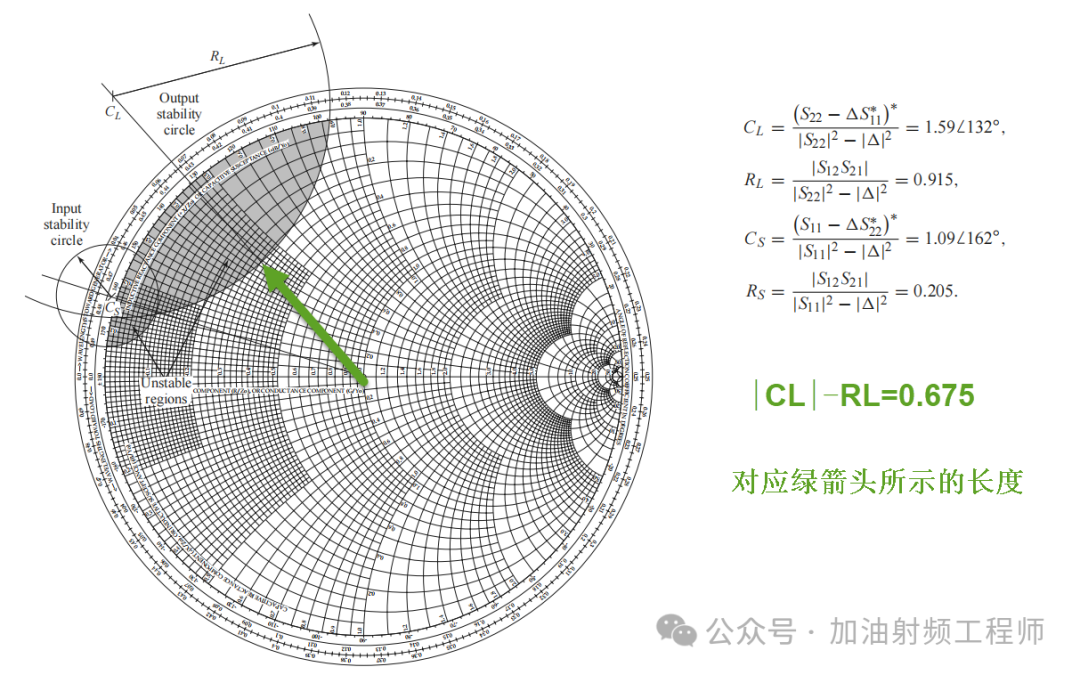
从这点看,当u越大,那就说明这个不稳定圆离SMITH圆图的中心越远,在SMITH圆图内的不稳定区域就越小,放大器就越稳定。
当u>1时,输出稳定圆在SMITH原图外,此时在SMITH圆图内没有不稳定区域,放大器无条件稳定。
参考文献:
[1] David M. Pozar, Microwave Engineering
[2] Marion Lee Edwards, Jeffrey H. Sinsky, A New Criterion for Linear 2-Port Stability Using a Single Geometrically Derived Parameter

课程吆喝处哈(已在平台上购买的同学,加我微信,领课件资料哈!)!
想了解接收机的底层理论知识,可以选择这门课;
想了解ADS的系统仿真,可以选择这门课;
想了解SystemVue的系统仿真,可以选择这门课。
想报名的同学,可以海报底部扫码哈!
