1 二项式分布推导计算
二项分布的推导过程主要基于组合数学和概率论的基本原理。假设有一个随机试验，每次试验只有两种可能的结果，通常称为“成功”和“失败”。成功的概率为p，失败的概率为1−p。现在进行n次独立重复试验，在这n次试验中成功k次的概率。
推导过程如下：
1) 确定组合方式：
首先，需要确定在n次试验中成功k次的组合方式有多少种。这可以通过组合数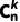
（也叫二项式系数）来计算，它表示从n个不同项中选取k个的不同方式的数目。组合数的计算公式为：
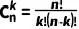(1)
其中n!表示n的阶乘，即 n×(n−1)×…×2×1。
2) 计算每种组合方式的概率：
接下来，计算每一种组合方式对应的概率。由于每次试验成功的概率是p，失败的概率是1−p，且试验是独立的，所以成功k次且失败n−k次的概率为pk×(1−p)n−k。
3) 将组合数与概率相乘：
最后，将组合数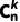与每一种组合方式的概率pk×(1−p)n−k相乘，并考虑到所有可能的k值（从0到n），得到成功次数为k的总概率。因此，二项分布的概率质量函数为：
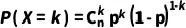k=0,1,2,…,n (2)
这个公式描述了在n次独立重复试验中成功次数为k的概率，即二项分布的概率质量函数。
需要注意的是，当n和k的值较大时，直接计算阶乘和组合数可能会非常繁琐。在实际应用中，通常会使用编程库中的二项式分布函数来进行计算，这些函数已经优化了计算过程，可以高效地处理大数值的情况。
2 从二项分布到泊松分布推导计算
从二项式分布推导泊松分布的详细计算过程涉及几个关键步骤和近似。逐步推导：
首先，回顾二项式分布的概率质量函数：
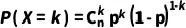k=0,1,2,…,n (3)
其中，X 表示在 n 次独立重复试验中成功的次数，p 是每次试验成功的概率。
现在，考虑一种特殊情况：当 n 很大，p 很小，但 np 保持为一个中等大小的常数时，二项式分布可以近似为泊松分布。
推导过程如下：
1) 使用斯特林公式近似阶乘：
斯特林公式给出了阶乘的一个近似表达式：
(4)
e 是自然对数的底数，约等于 2.71828。
利用这个公式，我们可以近似计算组合数：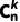
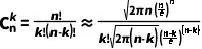(5)
简化后得到：
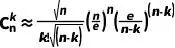(6)
2) 将 p 替换为 λ/n：
在泊松分布的上下文中，我们通常使用参数 λ 来表示平均发生率或期望值，即 λ=np。因此，可以将 p 替换为 λ/n得到
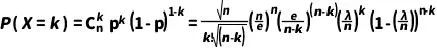(7)
进一步简化，考虑到 n 很大而 k 相对较小，并且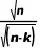
的影响在 n 很大时可以忽略。
。
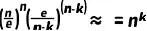上式子简化为
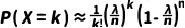(8)
根据指数函数的性质
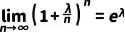(9)
3) 当 n 趋于无穷大时，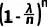
趋近于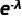 
（这是由指数函数的定义和性质得出的）。因此，上述(8)式进一步简化为：
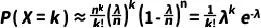(10)
这就是泊松分布的概率密度函数。综上所述，当二项式分布中的试验次数 n 很大，而每次试验成功的概率 p 很小时，通过一系列近似和变换，我们可以将二项式分布近似为泊松分布。这种近似在统计学和概率论中非常有用，特别是在处理大量小概率事件时。
3 泊松分布在分子免疫检测中的应用
在分子免疫检测中，泊松分布可以用于描述在一定区域内（如细胞表面、组织切片等）随机出现的抗原分子数量或者荧光标记分子的数量。例如：
1）流式细胞术分析
在流式细胞仪中，我们可能对单个细胞上特定抗原受体的数量感兴趣。假设平均每个细胞上有 λ 个受体，那么根据泊松分布，给定细胞上具有 k 个受体的概率可以通过泊松概率质量函数来计算：
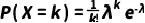
这有助于研究人员了解细胞群体中不同受体表达水平的细胞比例。
2）免疫组化或免疫荧光实验：
在这些实验中，抗体与组织切片上的靶蛋白结合后，通过显色剂或荧光探针进行可视化。每单位面积（如一个视野或一个细胞核内）的阳性信号点数可以服从泊松分布。
实验人员可能想要知道在一定的观察窗口内观测到 k 个信号点的概率，特别是在背景噪声较高的情况下，泊松分布可以帮助量化这一随机过程。
3）病毒或微生物计数：
分子免疫检测也包括对病毒颗粒、细菌或其他微生物的定量。例如，在病毒载量检测中，如果已知样本中的平均病毒浓度，泊松分布可以用来预测在一次检测中发现某个病毒拷贝数的概率。
4）基因表达定量：
在RNA测序（RNA-Seq）数据分析中，泊松分布模型有时也被用于估计转录本的丰度。尽管更为复杂的统计模型常被使用，但在某些简化条件下，基因表达水平的变化可以近似为泊松过程。
通过泊松分布的建模和计算，研究者能够更准确地推断出生物分子的实际分布情况，并以此为基础进行进一步的数据分析和统计推断。
4 计算实例
泊松分布可以被用来精确描述超低浓度蛋白分子的检测过程。以下是泊松分布在分子免疫检测中的一个具体计算示例：
假设我们正在检测一种特定蛋白质分子的浓度，其平均出现率为λ。为了简化计算，我们假设λ=3，即平均每个样本中有3个蛋白质分子。现在，我们想要计算在一个样本中检测到k个蛋白质分子的概率。这可以通过泊松分布的概率质量函数来完成。概率质量函数的公式为：
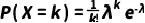
其中，X是观察到的蛋白质分子数，k是具体的次数，λ是平均出现率。
例如，我们想要计算在一个样本中检测到恰好2个蛋白质分子的概率。将λ=3和k=2代入公式，我们得到：
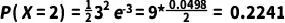
所以，在一个样本中检测到恰好2个蛋白质分子的概率约为0.2241。
假设在一项针对某种细胞表面抗原的流式细胞术实验中，我们已知平均每个细胞上大约有4个该抗原分子（λ=4）。现在想要计算在给定的一个细胞上观察到恰好有6个这种抗原分子的概率。
根据泊松分布的概率质量函数，可以这样计算：
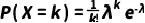
将 λ = 4 和 k = 6 带入公式：
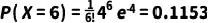
所以，在这个例子中，观察到一个细胞上有6个该抗原分子的概率约为11.53%。
类似地，我们可以计算其他k值的概率。如果我们想要知道检测到蛋白质分子数少于或等于某个特定值（比如3）的概率，我们可以计算所有小于或等于3的k值的概率，并将它们相加。这称为累积分布函数。值得注意的是，由于泊松分布的前提是事件之间是相互独立的，因此在实际应用中，需要确保样本中的蛋白质分子是随机分布的，且每个分子的检测是独立的。此外，λ的估计也是非常重要的，它可以通过实验数据或理论模型来得出。通过这种方法，泊松分布在分子免疫检测中为我们提供了一种精确量化超低浓度蛋白质分子的工具，对于生物医学研究和临床诊断等领域具有重要意义。
荧光分子计数中，泊松分布可以用于预测在某个区域内（如细胞内或显微图像的像素点）随机出现荧光标记分子的数量。例如，在单分子荧光成像实验中，我们对每个细胞内某种蛋白质分子的平均表达量为λ个。
假设研究者使用了荧光标记技术来检测和量化细胞内的某种蛋白质，并且通过分析得知，在一个典型细胞内平均有100个这种荧光标记的蛋白质分子（即λ=100）。现在他们想要计算在一个特定细胞内恰好观测到120个荧光信号的概率。
应用泊松分布概率质量函数：
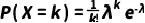
将 λ = 100 和 k = 120 带入公式：
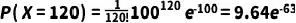
这个结果非常小，表示在给定条件下，观察到恰好120个荧光标记分子的概率极低。在实际数据分析时，通常会用泊松分布来拟合整个分子计数的数据集，以获得总体表达水平、变异性以及不同表达水平下的细胞比例等统计信息。
