ADC — 模数转换器是连接模拟世界与数字世界的桥梁。说到这里,有些朋友会问,我们为什么需要模数转换?为什么需要ADC?
简单来说,自然世界里面的很多信号,比如声音信号、手机信号、电视信号等,都是具有一定频率,以及带宽的信息。这些信息被我们所熟悉,但是这还不够的,我们希望这些信号能够被机器熟悉,被机器识别,从而达到信息的传递,以及物物相连。机器能够识别的是数字信号,能够处理的也是0101的数字信号,所以说ADC是让一些模拟信息能够被MCU,DSP,FPGA这些处理器处理的媒介。如图一 ADC转化过程。
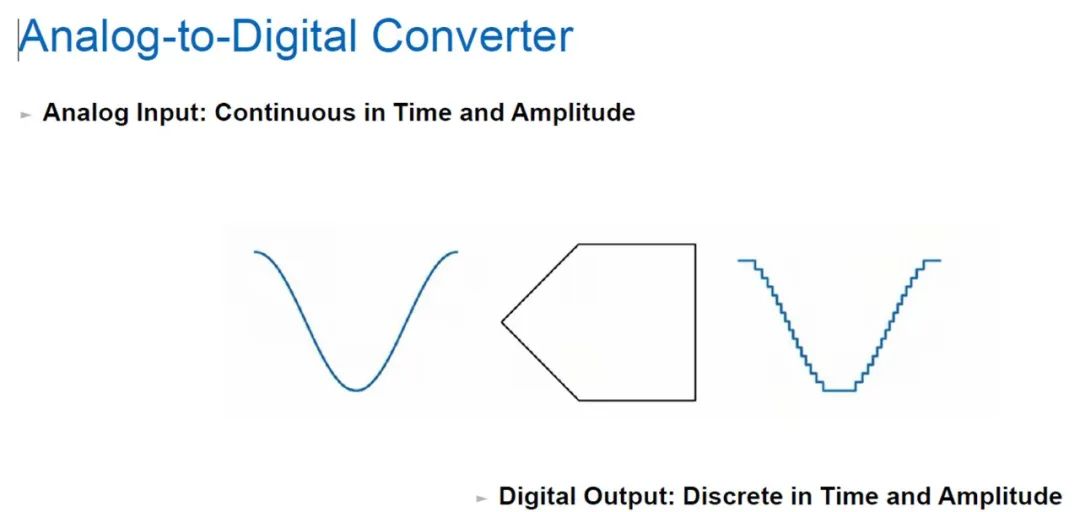
图一 ADC转化过程
什么是Sigma-Delta ADC?
Sigma-Delta ADC一般由Σ-Δ调制器和降采样抽取滤波器组成,以远高于Nyquist频率的采样频率对输入信号进行采样,采样后的信号经调制器处理后转换为低位高码率的数字信号流。
也就是ADC里面分为两部分,一部分是调制器,另一部分是可配置数字滤波器,调制器的作用是将模拟信号完成模数转化并整形,数字滤波器的作用是抽取,平均,滤波。整个过程都是在ADC内部完成的,ADC将数据流通过SPI总线总线传递给MCU。如图二 Sigma-Delta ADC 内部框图
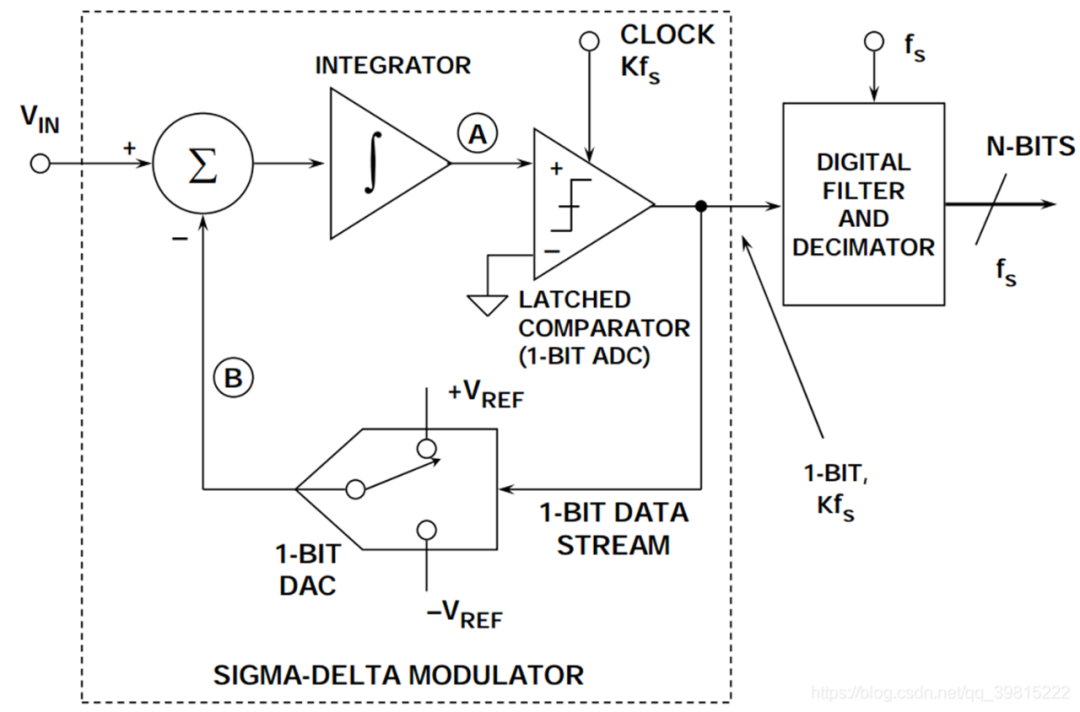
图二 Sigma-Delta ADC 内部框图
Sigma-Delta ADC的主要优势是超高信噪比,换句话说就是有效位数高,通俗地讲就是精度高,测得准。目前24位,32位的Sigma-Delta ADC非常多,已经不是很稀缺了,缺点也很明显,处理信号的带宽相对来说比较窄,这是由于我们在设计此类ADC的限制,保留采样信号中的低频信息,滤除高频噪声。
如图二左半部分就是Σ-Δ调制器,它包含一个加法器、积分器、一个比较器和一个1Bit DAC。右半部分就是降采样抽取滤波器,那么它们是如何配合工作呢?
Sigma-Delta ADC如何实现高精度高性能?
1、过采样
过采样技术在1946年被首次提出,是指用远大于Nyquist频率的采样频率对输入信号进行采样,用过采样率(Over Sampling Ratio, OSR)来衡量过采样程度。OSR与信号带宽fb之间的关系为:OSR=fs/(2fb)。
过采样技术会给ADC带来两个优势:首先,较高的采样频率会降低前级抗混叠滤波器的设计要求,过渡带可以稍微平滑;其次,过采样技术可以提高信噪比。当采样频率提高时,量化噪声的功率谱密度Se(f)会随之降低,从而提高带宽内的信噪比,如图三所示。
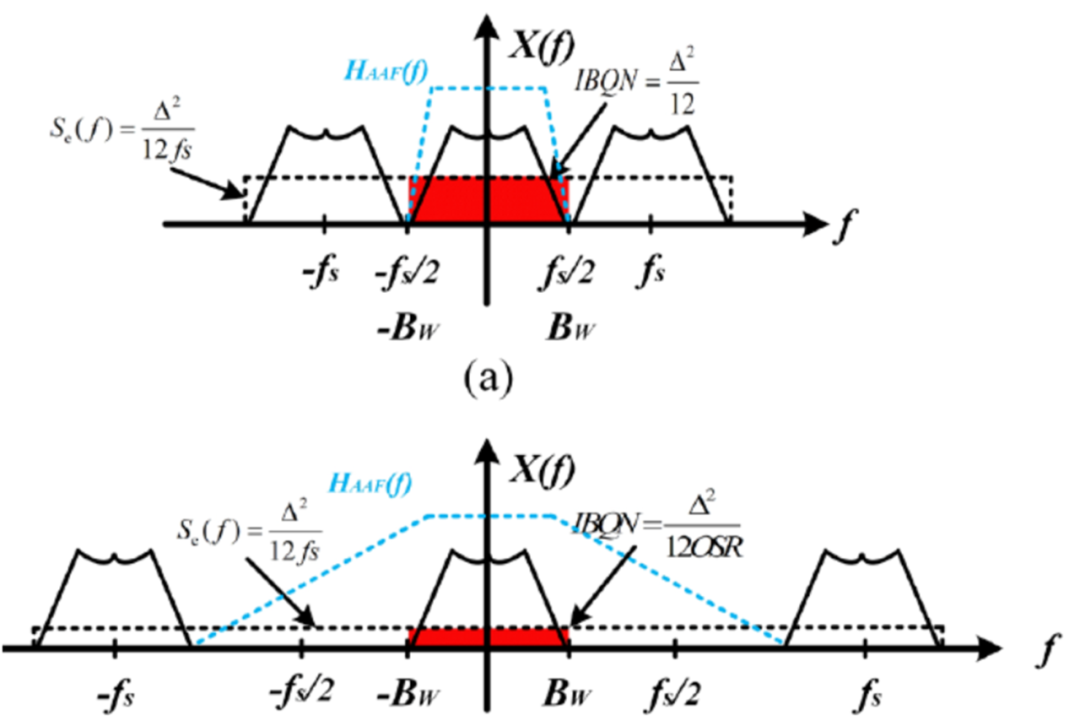
图三 过采样示意图
a代表常规的奈奎斯特采样,b代表过采样
怎么去理解这个图呢,我们都知道采样定理,通常的我们的采样频率应该是大于输入信号的2倍以上,我们采样后信号才不会出现混叠,信号信息才不会丢失,如图三a所示,此时的fs/2刚好等于输入信号最大频率,此时的量化噪声的功率谱密度:
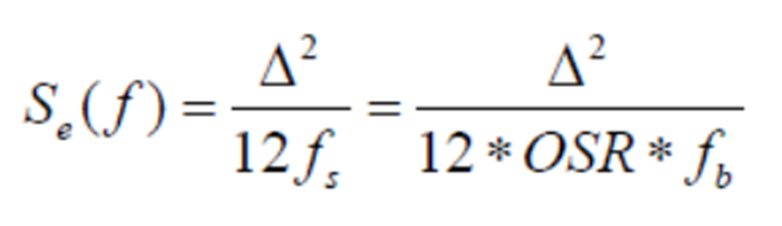
当采样频率提高时,Se(f)降低,即量化噪声的功率谱密度降低,这有点类似我们电源里面的扩频技术;另外一方面,过采样之后,我们的抗混叠滤波器就比较好设计了,因为如上图表现,Haaf(f) 设计一个低阶的平滑的低通滤波器就足够了。
2、量化噪声整形
过采样技术能有效降低信号带宽内的量化噪声,但仅通过增大采样频率来提高ADC的信噪比,会大幅度增加功耗,提高电路设计难度。因此,Sigma-Delta ADC的另一种精度提升技术——噪声整形技术于1954年首次提出,基本原理是改变量化噪声在频谱上的分布,将低频噪声搬移到高频,经后级数字抽取滤波器可以滤除信号带宽外的大部分噪声,从而提高带宽内的信噪比,如图四所示。
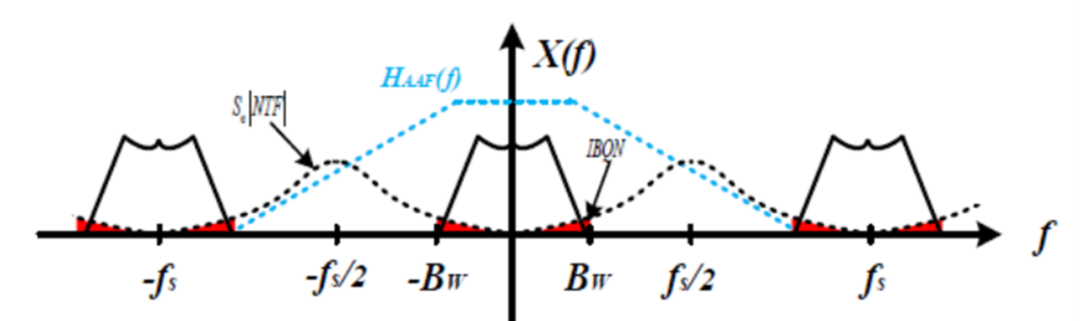
图四 整形后的量化噪声
噪声整形技术是通过利用积分器来构建具有高通特性的环路滤波器,对量化噪声进行整形,具体的公式推导此处就省略了,最后的量化噪声公式类似于一个正弦波。
由图可见,频率越低,噪声也越低,噪声频谱不再类似于矩形,而是变为幅度与频率相关的类似于正弦波的波形。这样的话,量化噪声在低频段的能量谱密度更小,信号带宽内的总噪声越小,那么信号的载噪比就提升上去了,性能就提升了。
3. 数字抽取滤波
可以理解为通过数字滤波器后将调制器的数字输出的N位加起来,然后取平均值,这样的话,相当于输出速率降低了,但是采集的数值更加接近于此段时间的平均值,如图五,可以看看Sigma-Delta ADC的采样过程。
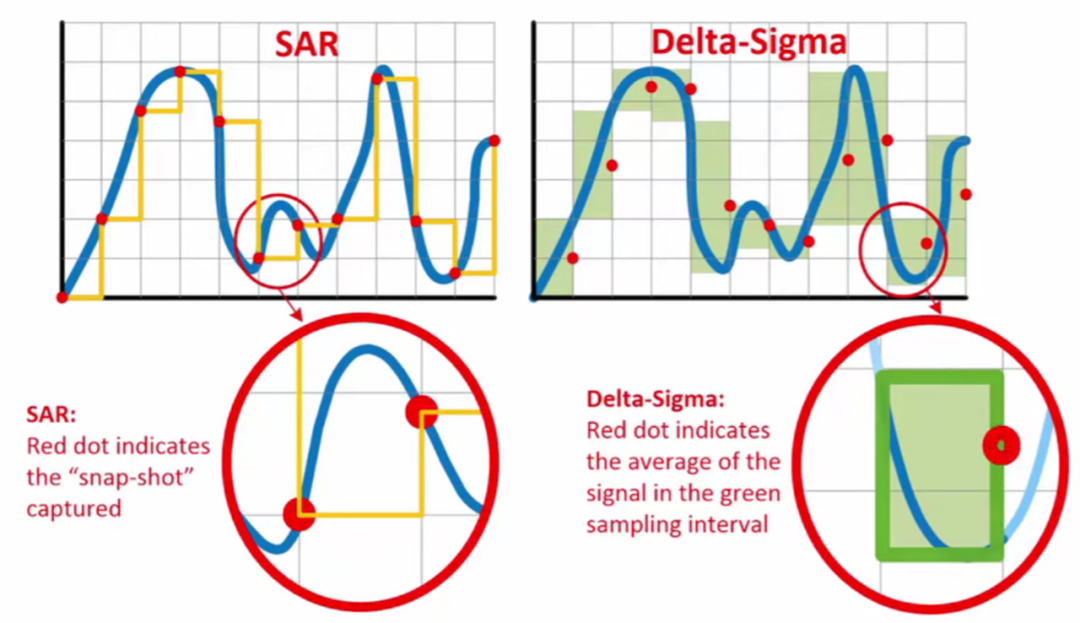
图五 Sigma-Delta ADC的采样过程以及与SAR采数区别
Sigma-Delta ADC的应用

扫一扫订阅新闻邮件,及时获取最新技术资讯

