统计学-随机变量

我发现微积分，线性代数，概率，统计，这四个学科有点难舍难分。但是应该从微积分，线性代数这样学才是对的，不然你是看不懂统计和概率的。

统计学是说两个事情，一堆数据如何描述，以及数据如何推断。

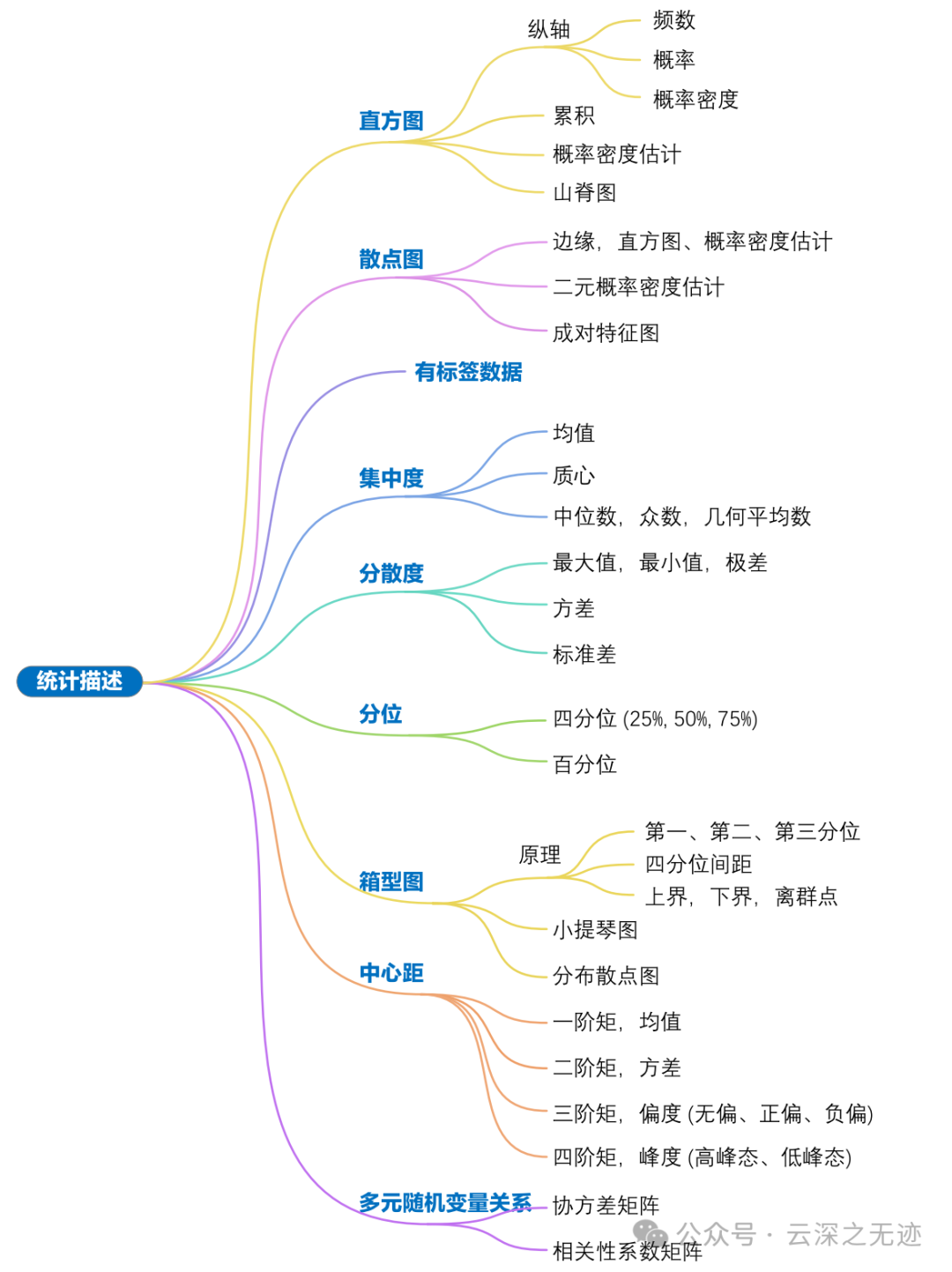
统计描述 (descriptive statistics) 是指对数据进行整体性的描述和概括，以了解数据的特征和结构。统计描述旨在通过一些表格、图像、量化汇总来呈现数据的基本特征，比如中心趋势、离散程度、分布形态等。统计描述通常是数据分析的第一步，可以帮助我们了解数据的基本情况，判断数据的可靠性、准确性和有效性。 

在大学第一次学这些内容的时候，并不能很好的理解全部的内容，但是一年多的工程实践，让我有了那么一点点的全局的感觉。

“随机变量不同于代数中的变量，因为它具有一组完整的值，并且可以随机获取任何值。代数中使用的变量一次不能具有多个值。如果随机变量X = {0,1,2,3} 那么X可以是随机的0、1、2或3，其中每个都有不同的概率。”

随机变量

统计描述

随机变量是指变量的值无法预先确定仅以一定的可能性(概率)取值的量。它是由于随机而获得的非确定值，是概率中的一个基本概念。 

因变量

变量拥有这些特点

随机变量在统计和概率中非常重要的概念，必须先具有随机变量，才会有后续概率分布的概念。

随机变量用来表示随机现象的结果，可以看成一组值，每个值都有一定的概率被取到。

我感觉以前没有学好的原因就是一些基础概念的不理解。

接下来就是概率：

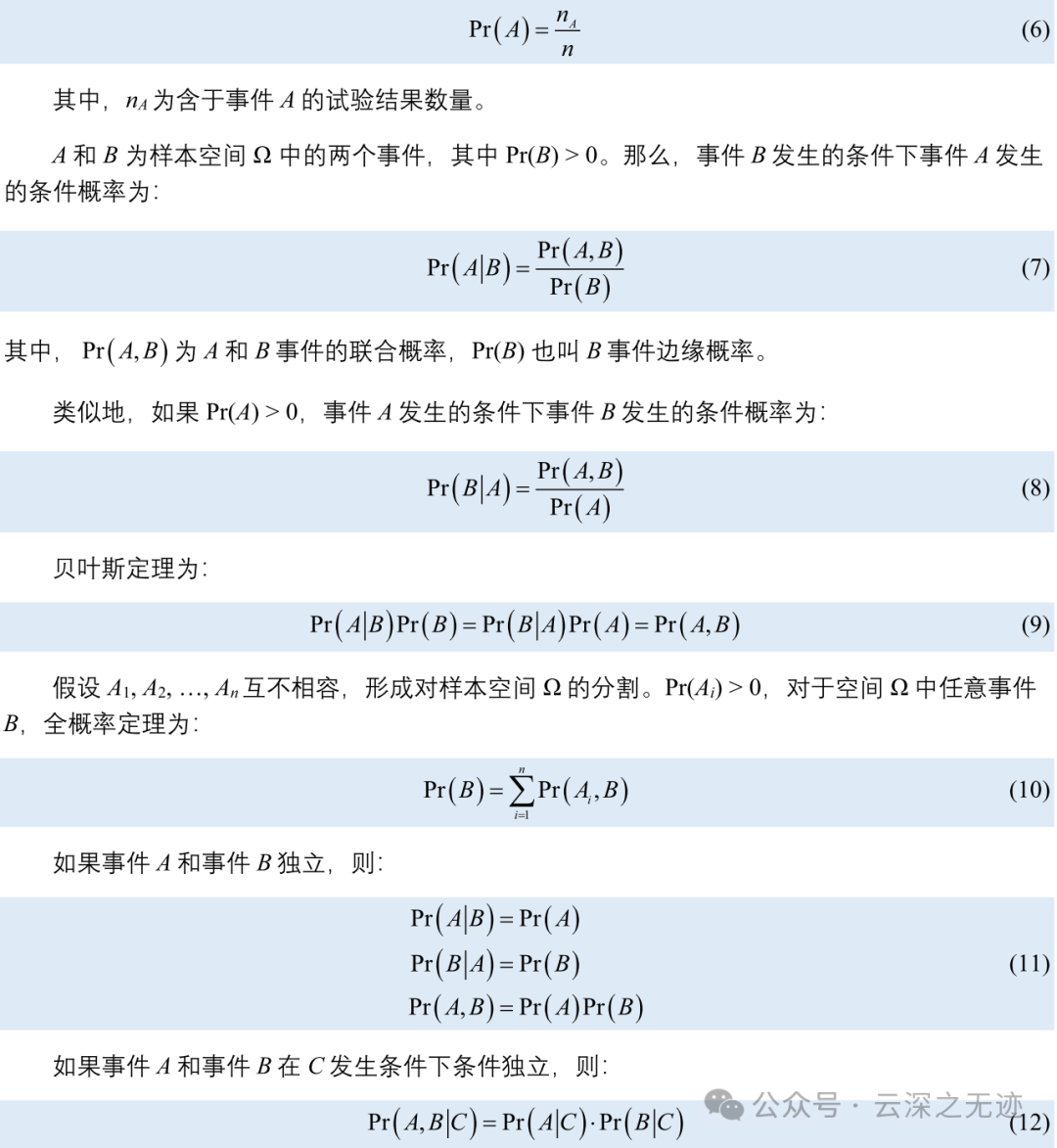
古典概率空间

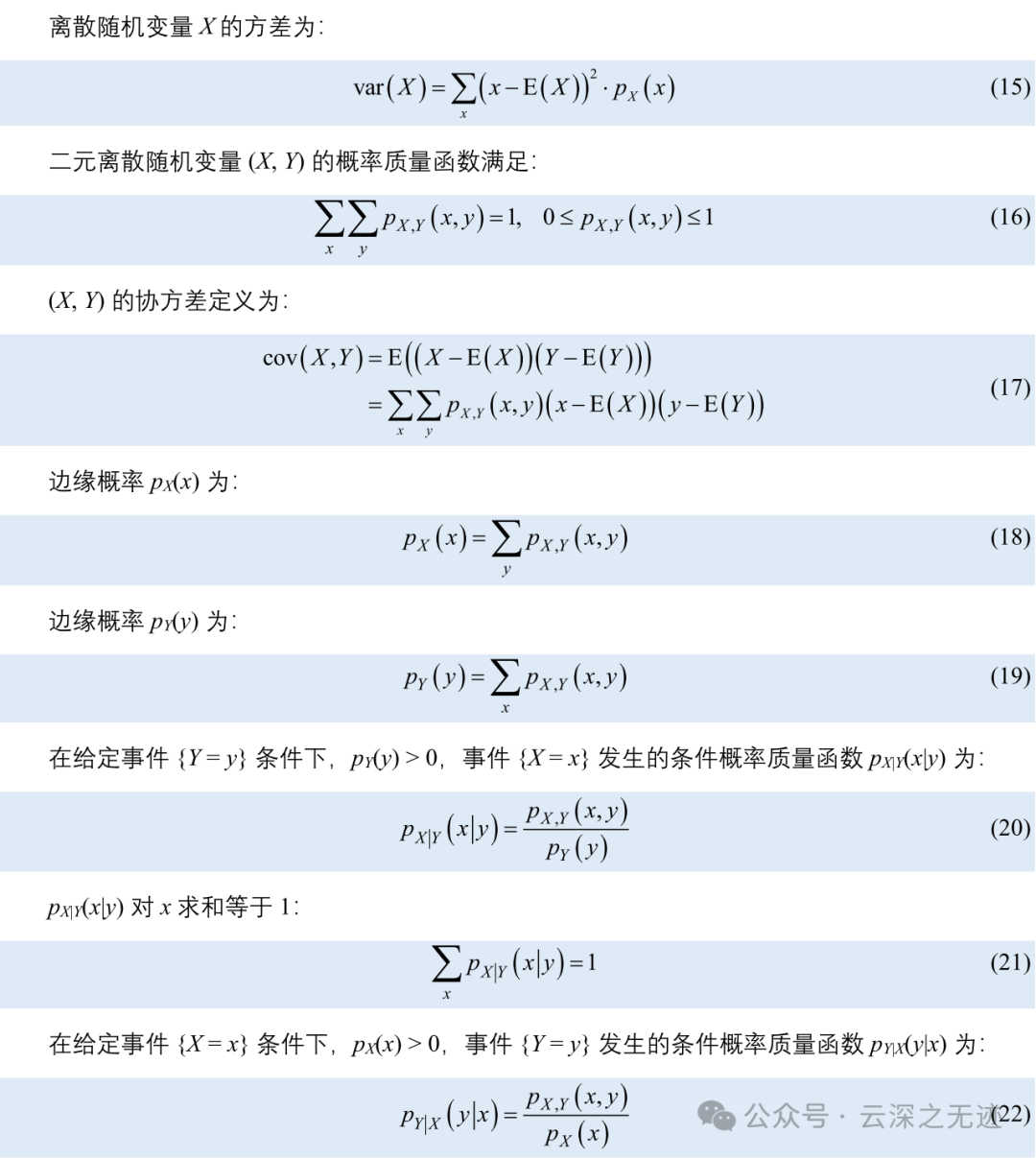
就是这样的

比值就行

这里插一句，其实上面的分类有些混乱，其实研究完随机变量，就是研究多高多个随机变量之间的关系。

先看两个变量之间的关系

这样的，就无非是发生和不发生以及有顺序在

再补一个条件概率：

条件概率（英語：conditional probability）就是事件A在事件B发生的条件下发生的概率。条件概率表示为P（A|B），读作“A在B发生的条件下发生的概率”。边缘概率是某个事件发生的概率。联合概率是两个事件一起发生。

总结一下：

这一趴算OK

至于为什么是古典概率，大概就是因为在古代大家就在研究这个。

这些个是离散随机变量，我这里就有点知识匮乏了

高斯分布就不放了，我搞不懂了

接下来看统计描述：

书里面吧，人家公式啥的写的更详细，我这里就盗图了。

用Adobe Illustrator美化matplotlib输出图

书是使用的上面文章里面的书。

直方图通常将样本数据分成若干个连续的区间，也称为“箱子”或“组”。直方图中矩形的纵轴高度可以对应频数、概率或概率密度。

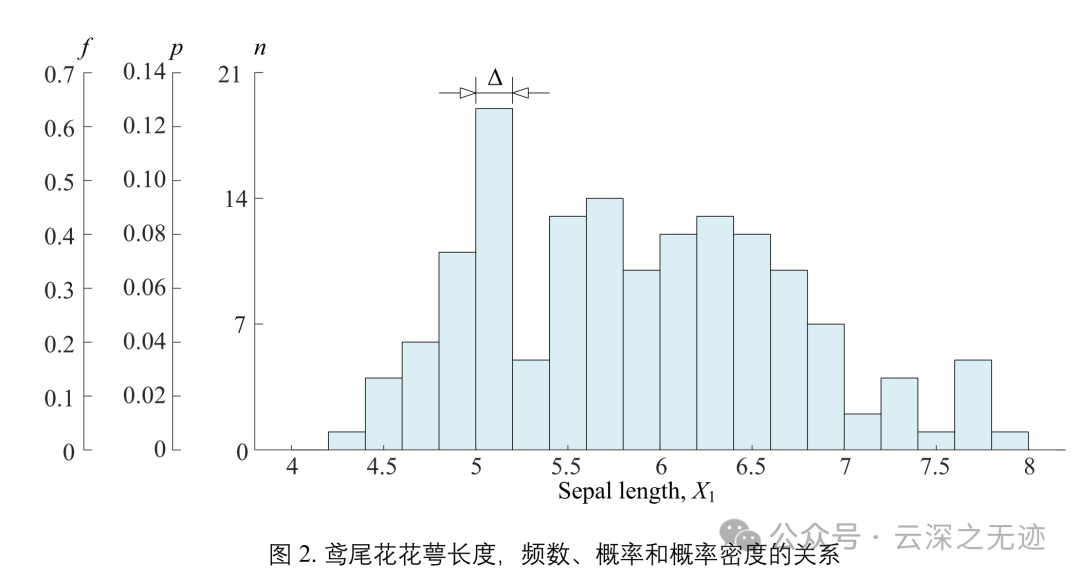
一般我们使用的时候，频数用到最多。

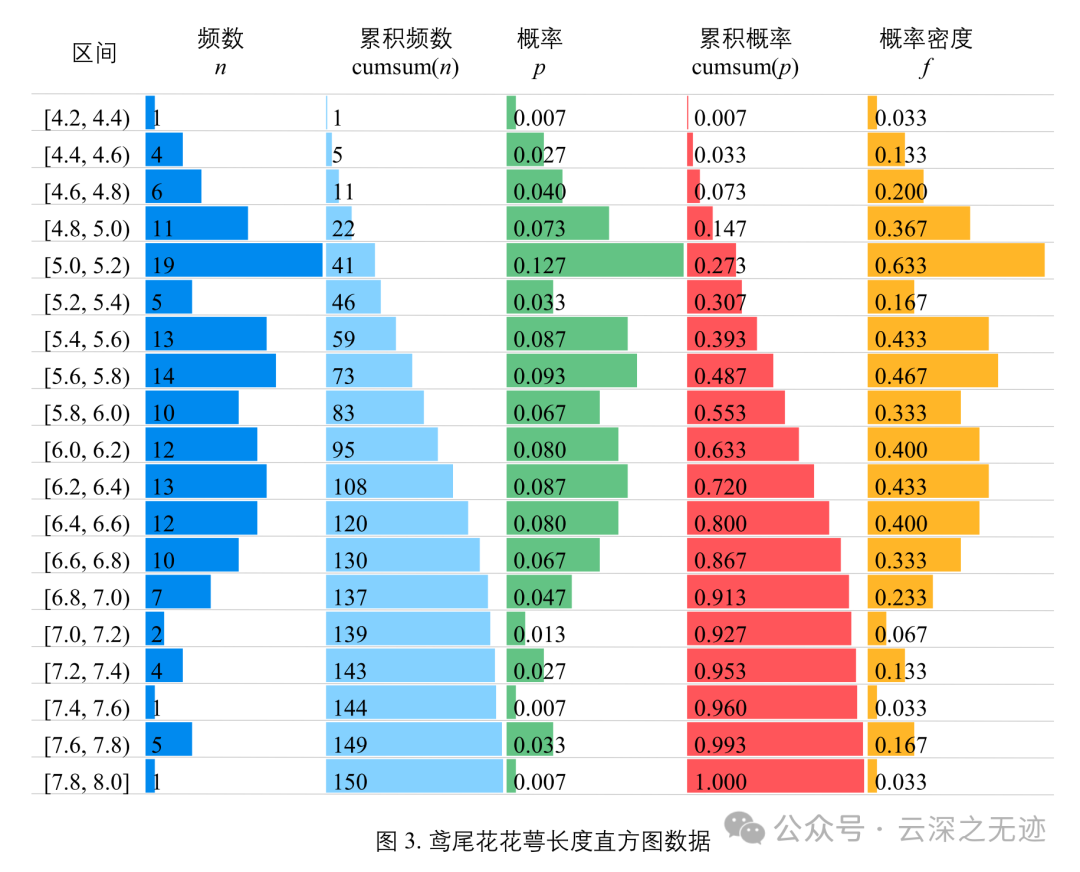
你看这个图多漂亮，就算不懂都一目了然

频数，也叫次数，是指在一定范围内样本数据的数量。显然，频数为非负整数。

频数除以样本总数的结果做概率

概率除以组距得到的是概率密度 (probability density)

积分是什么？

先不管哪些公式啥的，就记住我说的话：指的是对函数的积累总和或面积的计算过程。在微积分中，积分是求解函数的定积分或不定积分，用于计算曲线下面积、求函数的反导数等。

就是加起来，求和，至于把什么加起来再说，反正就先认为是加起来。

就是积分这个Fx，从a到-♾️

这里补充一个知识：

一开始文章里面的这个地方的♾️是没有符号的，感谢王老师

记住积分的区间

王老师口中的累积概率函数也是概率分布函数的意思

概率密度函数描述的是随机变量在某个取值点的概率密度，是描述随机变量分布的基本函数之一。

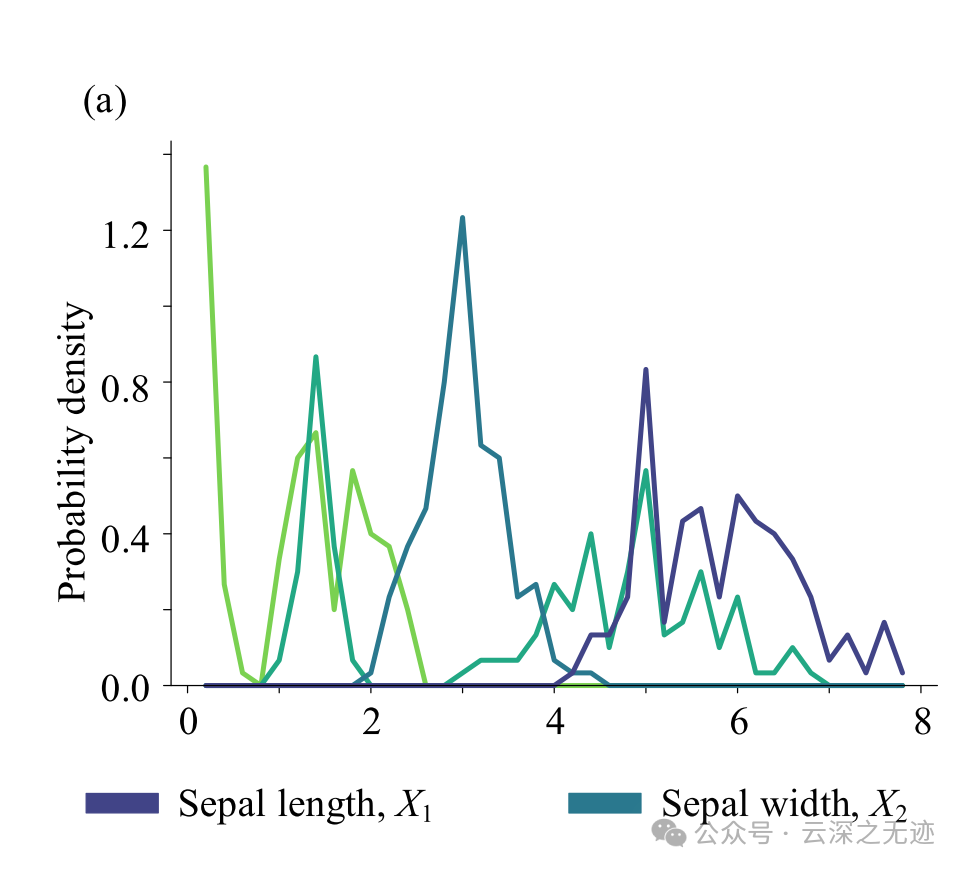
纵轴是概率密度，你可以看下面的值，对应的密度是多少

名词出现，概率密度？其实很多时候都是从物理上面拉概念。

概率密度（Probability Density），指事件随机发生的几率。概率密度等于一段区间（事件的取值范围）的概率除以该段区间的长度，它的值是非负的，可以很大也可以很小。

在实际问题中，往往无法直接获得概率密度函数，因此需要通过概率密度估计来估计概率密度函数。

概率密度函数：在数学中，连续型随机变量的概率密度函数（Probability density function，简写作PDF），在不致于混淆时可简称为密度函数，是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。

下图中，横轴为随机变量的取值，纵轴为概率密度函数的值，而随机变量的取值落在某个区域内的概率为概率密度函数在这个区域上的积分。

当概率密度函数存在的时候，累积分布函数是概率密度函数的积分。

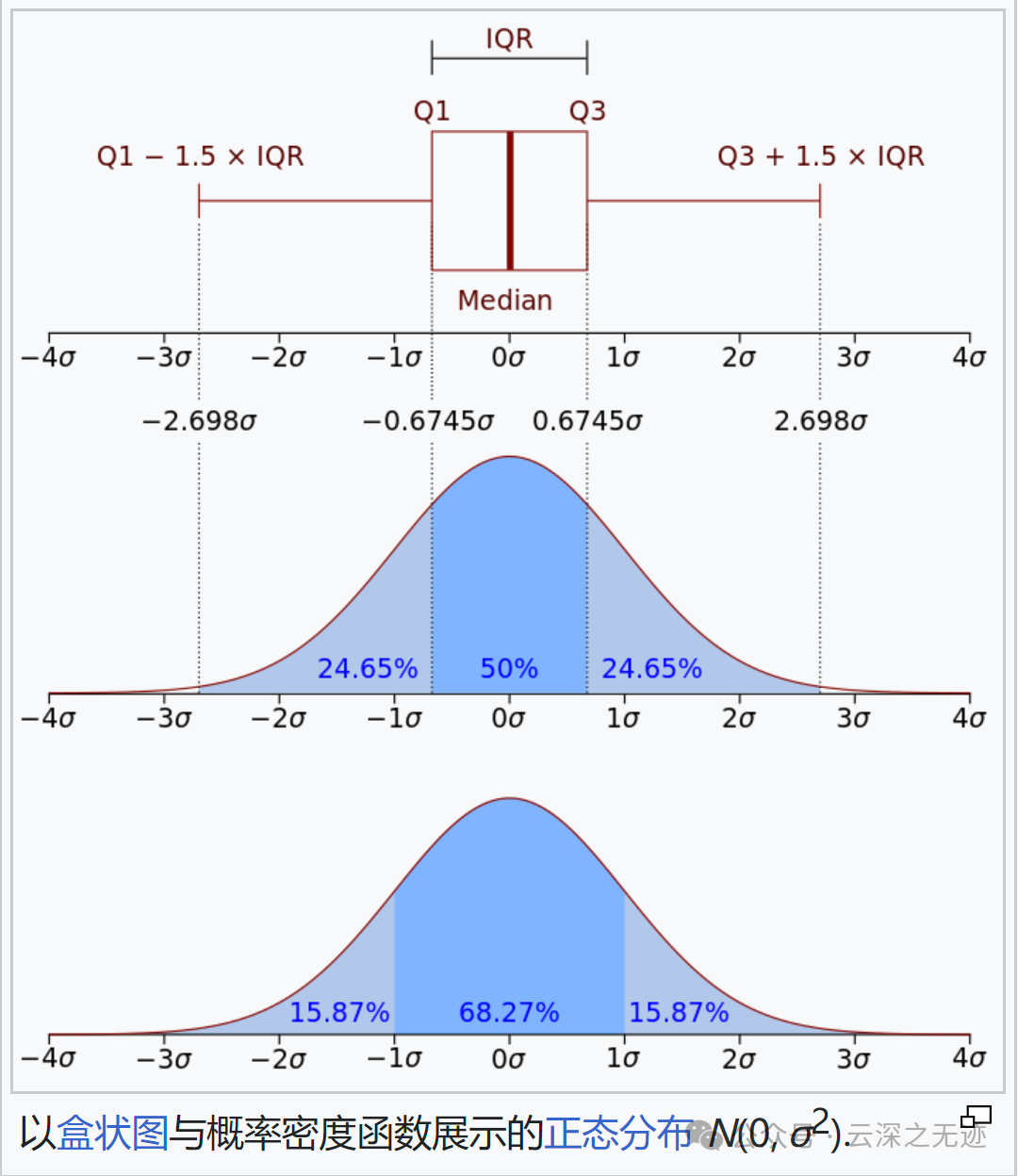
图就是这样

概率密度函数可帮助确定随机变量值的较高和较低概率的区域。

对于离散变量，PDF 将给出给定 x 值的概率值。例如，糖果制造商生产多种颜色的某一类型糖果。生产的糖果中有 30% 为黄色，10% 为橙色，10% 为红色，20% 为绿色，30% 为蓝色。

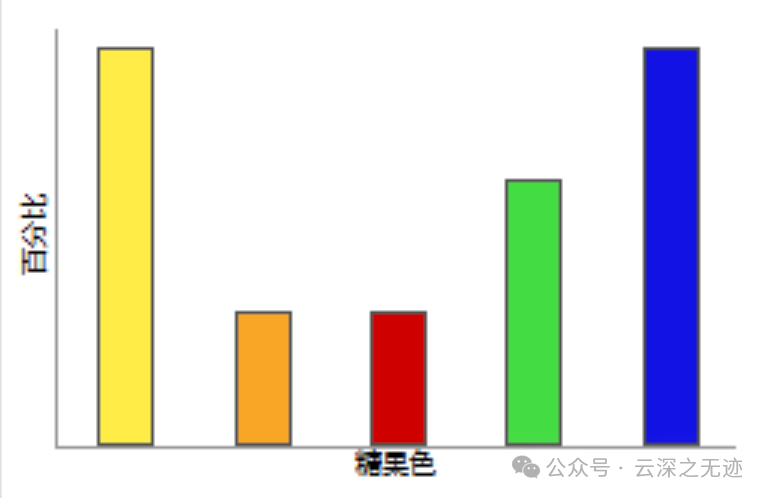
概率密度函数 (PDF) 是一个用于表示连续随机变量的概率分布的等式。例如，为葡萄酒瓶切割软木塞的机器可产生直径不同的软木塞。在下面的软木塞直径条形图中，每个条形表示具有相应直径的软木塞的百分比。

曲线是软木塞直径的 PDF。可使用 PDF 确定随机变量值的较高和较低概率的范围。例如，只有较小百分比的软木塞 (1%) 直径小于 2.8 厘米。

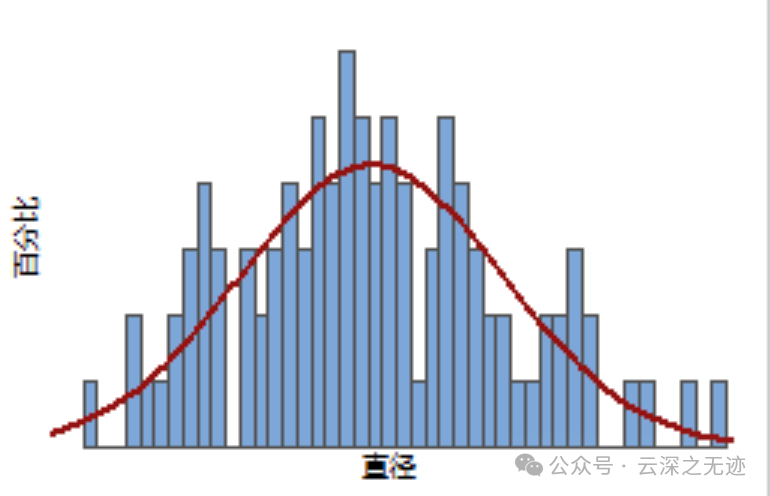
这个图不咋样

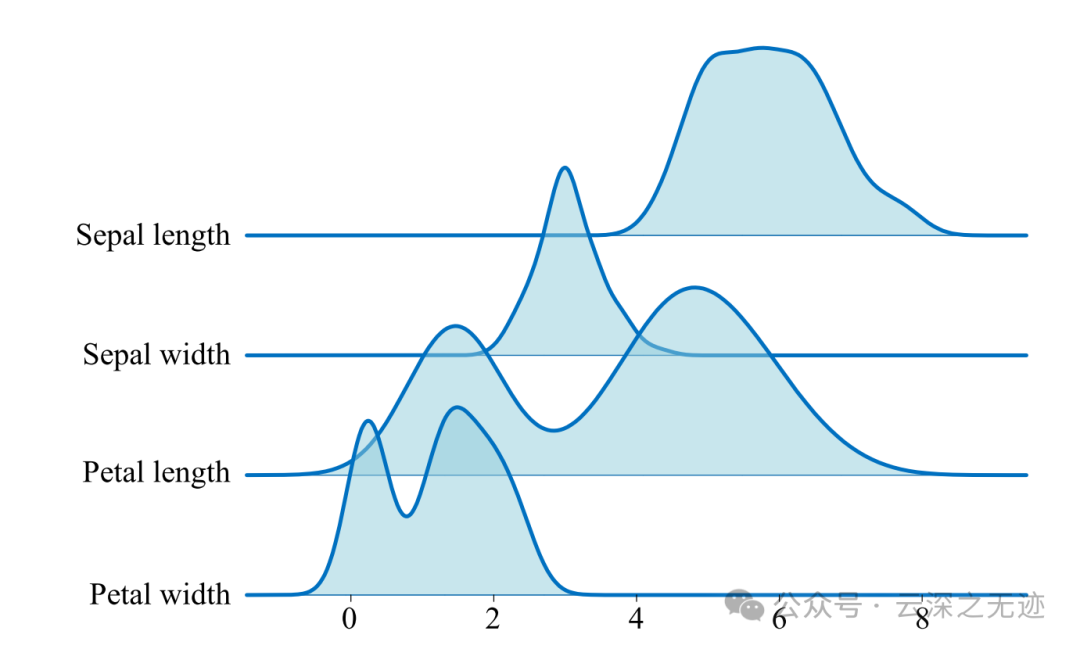
山脊图

散点图常用于探索数据中的异常值、趋势和模式，并且可以发现变量之间的相互作用和关联性。

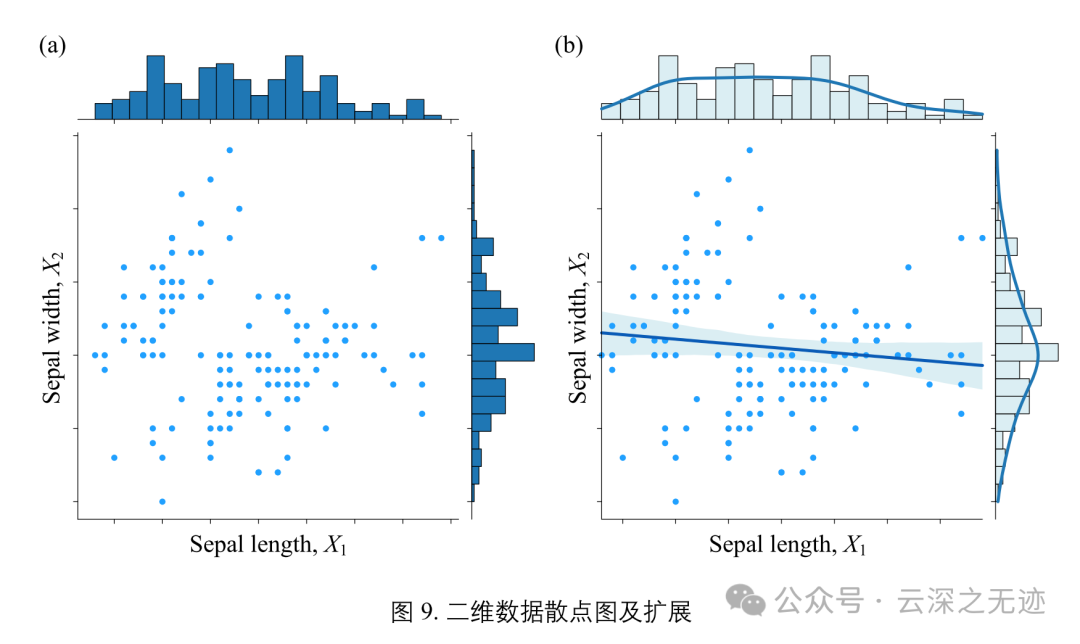
散点图还可以进行扩展，就是在边缘做计算

左是边缘直方图，右是加了概率密度曲线

其实就是变量之间的关系的可视化。

这里说一下使用的这个数据集：

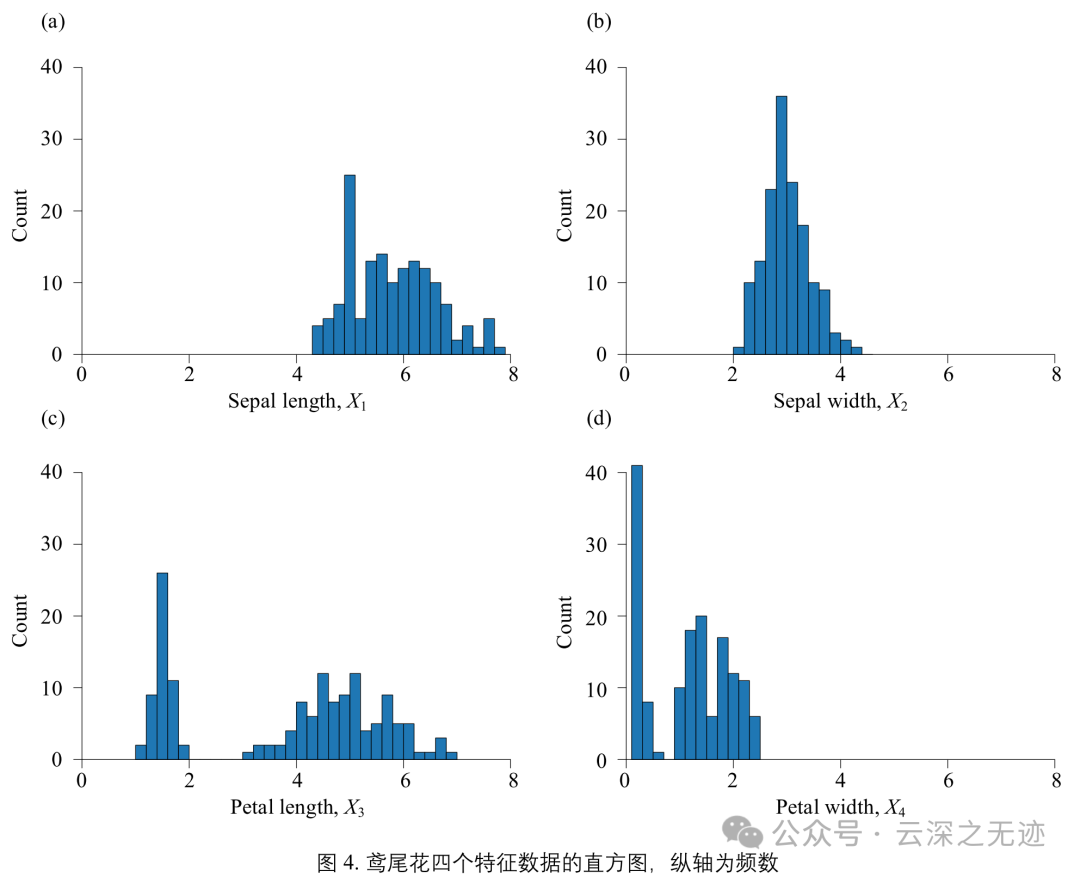
鸢尾花数据集共收集了三类鸢尾花，即Setosa鸢尾花、Versicolour鸢尾花和Virginica鸢尾花，每一类鸢尾花收集了50条样本记录，共计150条。

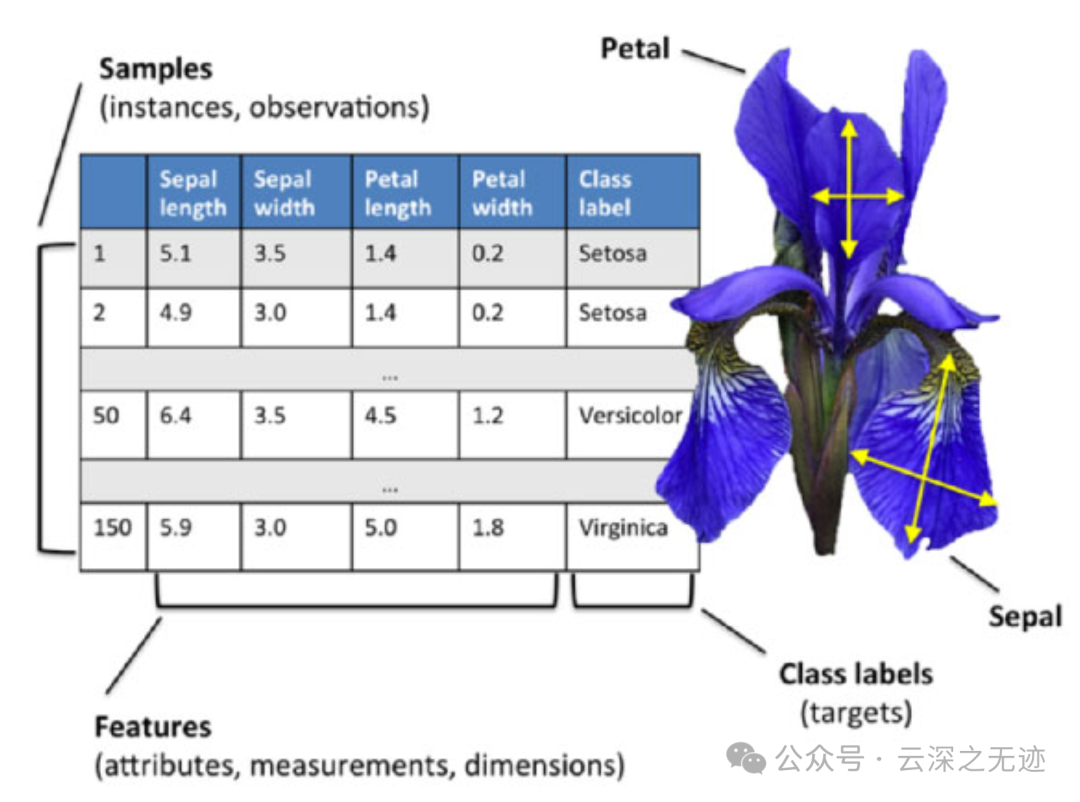
数据集包括4个属性，分别为花萼的长、花萼的宽、花瓣的长和花瓣的宽。对花瓣我们可能比较熟悉，花萼是什么呢？花萼是花冠外面的绿色被叶，在花尚未开放时，保护着花蕾。四个属性的单位都是cm，属于数值变量，四个属性均不存在缺失值的情况，字段如下：

• sepal length（萼片长度）

• sepal width（萼片宽度）

• petal length（花瓣长度）

• petal width （花瓣宽度）

• Species（品种类别）：分别是：Setosa、Versicolour、Virginica

单位都是厘米。

数据集是很小的

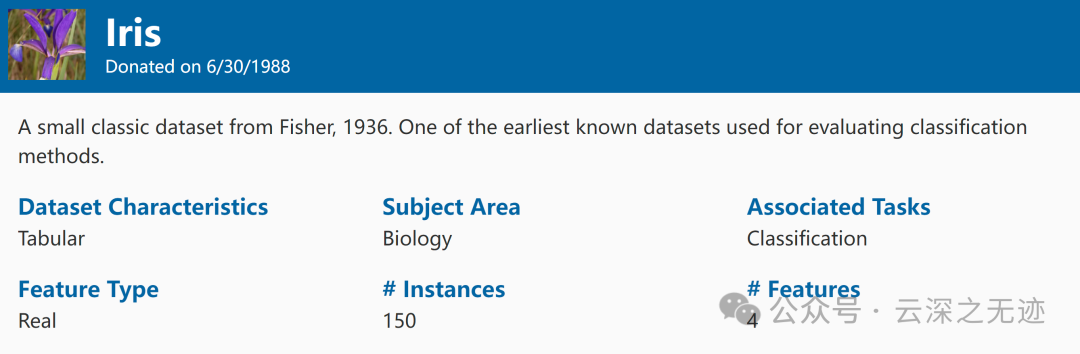
官方的位置

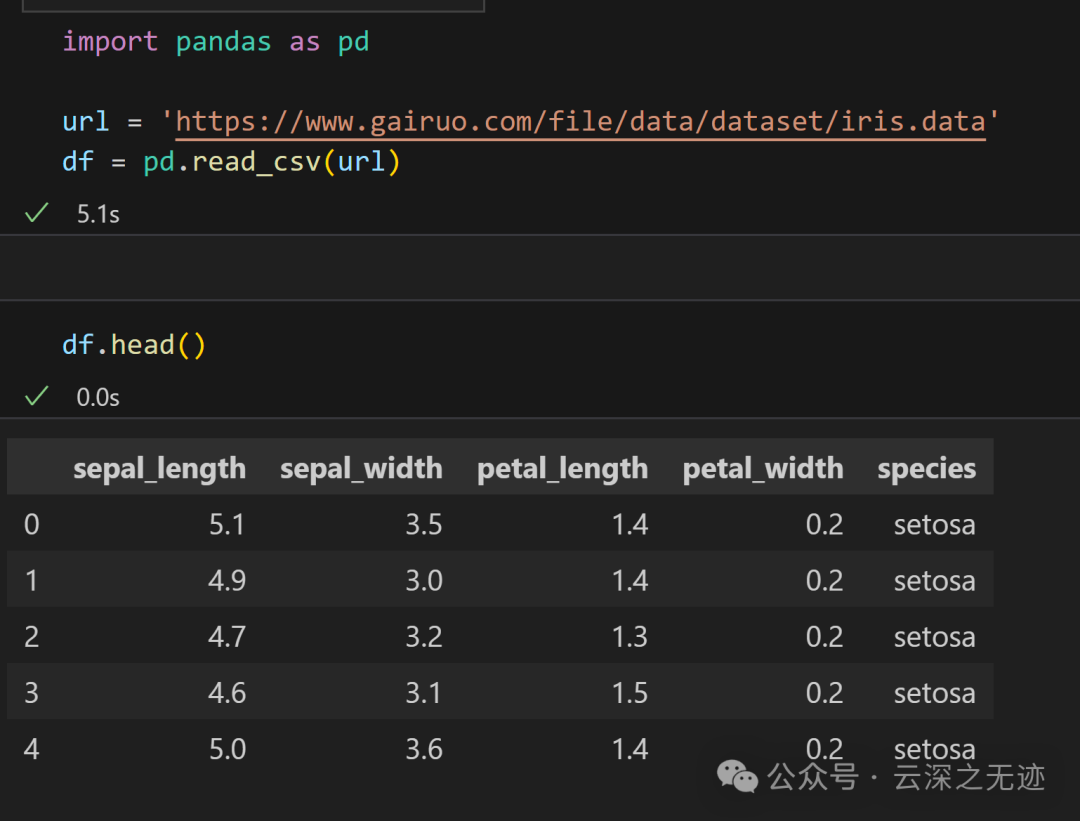
可以用pandas来下载

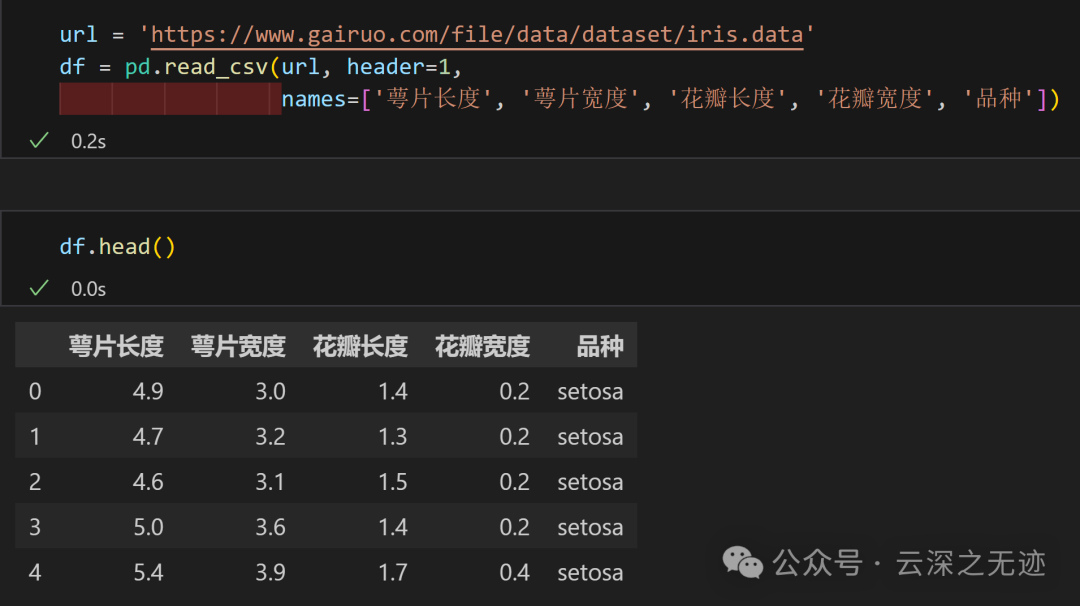
我们简单的来进行一个替换

接下来安装一下Spyder

可以安装一个插件开启notebook

看看优点

看看补全

但是这个Jupyter的插件是无法在安装的

这个是信号与系统里面的内容，看到了这个概密度函数

一个函数如果满足如下条件，则可以称为概率密度函数：

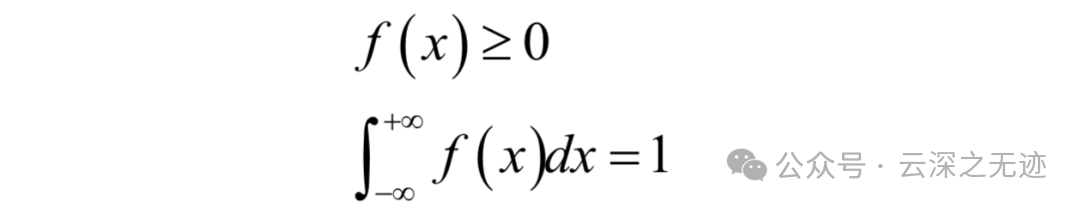
这可以看做是离散型随机变量的推广，积分值为1对应于取各个值的概率之和为1。

分布函数是概率密度函数的变上限积分，它定义为：

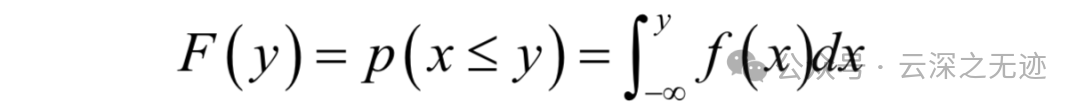
显然这个函数是增函数，而且其最大值为1。分布函数的意义是随机变量的概率。注意，连续型随机变量取某一个值的概率为0，但是其取值落在某一个区间的值可以不为0：

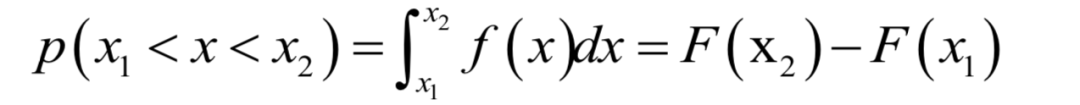
虽然连续型随机变量取一个值的概率为0，但取各个不通过的值的概率还是有相对大小的，这个相对大小就是概率密度函数。这就好比一个物体，在任意一点处的质量为0，但在这一点有密度值，密度值衡量了在各点处的质量的相对大小。

从这个角度，我们可以将概率密度函数解释为随机变量落在一个区间内的概率与这个区间大小的比值在区间大小趋向于0时的极限：

这个过程如下图所示：

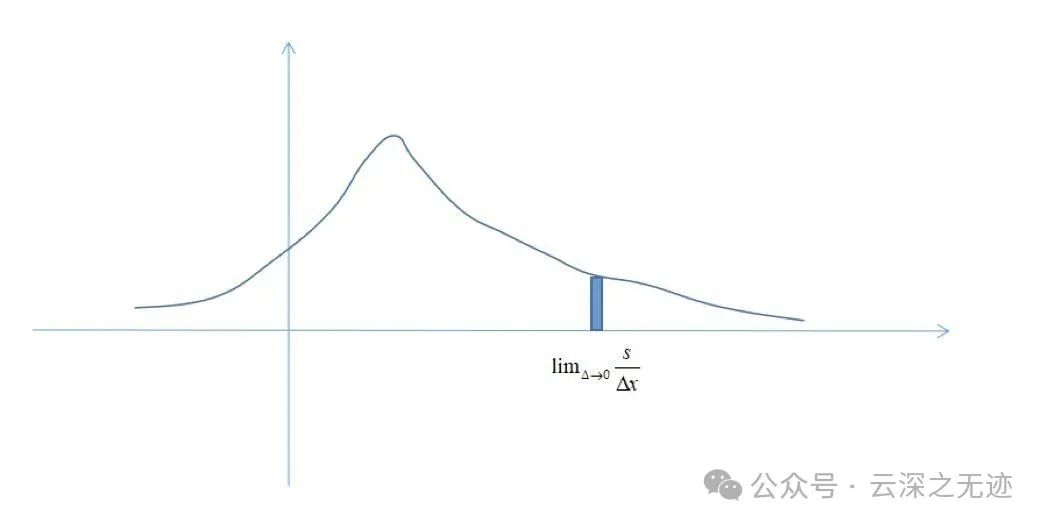
还是以上面的正方形为例，如果要计算随机点(x, y)都落在区间[0, 0.5]内的概率，可以这样计算：

这个面积，就是积分值，对应于分布函数。最常见的连续型概率分布是正态分布，也称为高斯分布。它的概率密度函数为：

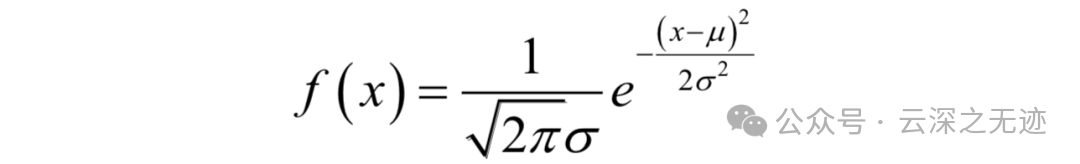
其中μ和σ分别为均值和方差。现实世界中的很多数据，例如人的身高、体重、寿命等都近似服从正态分布。

另外一种常用的分布是均匀分布，如果随机变量x服从区间[a,b]内的均匀分布，则其概率密度函数为：

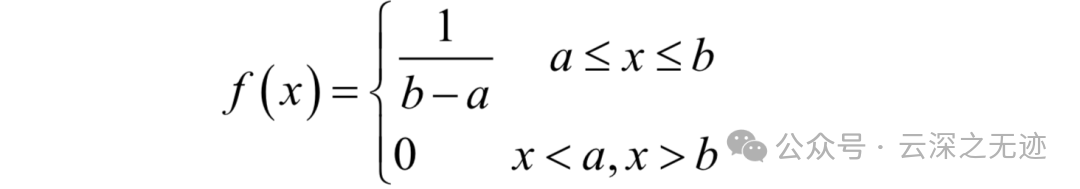
在程序设计和机器学习中，这两种分布是最为常见的。

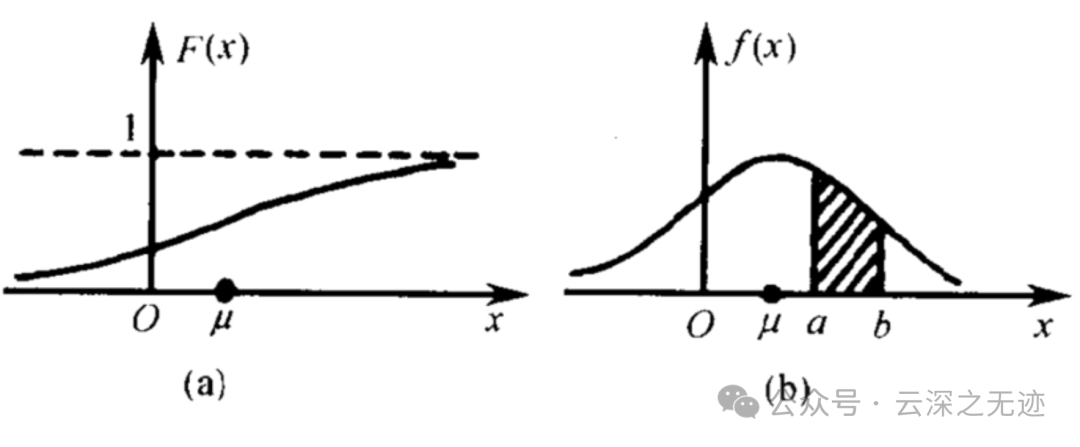
概率密度函数用数学公式表示就是一个定积分的函数，定积分在数学中是用来求面积的，而在这里，你就把概率表示为面积即可。

本来是感觉这本书非常有用，但是发现还是要数学知识扎实才能看爽

不过在此之前也可以先看看这个

接下来的文章如果会发的话，那就是要上强度了。

https://cloud.tencent.com/developer/article/1514756

https://zhuanlan.zhihu.com/p/48140593

https://github.com/Visualize-ML/Book5_Essentials-of-Probability-and-Statistics

https://juejin.cn/post/7141566114412101662

https://www.gairuo.com/p/iris-dataset

http://archive.ics.uci.edu/dataset/53/iris

https://support.minitab.com/zh-cn/minitab/21/help-and-how-to/probability-distributions-random-data-and-resampling-analyses/supporting-topics/basics/using-the-probability-density-function-pdf/