近期,上海交通大学机械与动力工程学院张文明教授团队在传感器领域著名期刊《IEEE Sensors Journal》上发表文章“Design and sensitivity analysis of a micro-resonant accelerometer with adjustable stiffness”,提出了多电极分布式静电驱动MEMS谐振加速度计的设计方案,并通过施加控制电压实现了谐振梁的刚度调控,理论和实验研究了MEMS谐振加速度计的多模态动力学特性和检测性能,对提高谐振加速度计灵敏度和克服非线性谐振传感系统中峰值频率对驱动强度的依赖性有重要意义。本文第一作者是山东理工大学李磊副教授,通讯作者是张文明教授。
内容摘要
本文采用分布式静电驱动形式设计了一类刚度可调式MEMS谐振加速度计,在实现高频模态驱动和提高谐振加速度计灵敏度方面具有很大潜力。首先,设计并制备了一个由敏感质量块、谐振梁、单驱动电极、双调节电极和单传感电极组成的谐振加速度计,并对其动力学行为进行了表征。然后,基于前三种弯曲振动模式,分别实现了85 Hz/g、134 Hz/g和135Hz/g的加速度检测灵敏度,并通过开环响应对谐振加速度计中谐振梁的性能进行了全面评估。通过理论预测和实验测量发现,随着调节电极上施加的控制电压增加,可以有效地提高谐振加速度的灵敏度和信噪比。特别是当谐振梁工作在临界屈曲附近时,基于基频模态振动检测的灵敏度可以从85Hz/g提高到4920Hz/g。最后,实验证明了由调节电极产生的静电力可以克服由几何刚度硬化引起的频率-振幅依赖性。本文研究结果为高灵敏度线性谐振加速度计的设计提供了理论指导和实验支持。
图文解析
MEMS谐振式加速度计能够利用频移实现加速度信号的精确感知,由于其体积小、灵敏度高、重量轻、能耗低和便于集成等优点,在导航制导、重力探测、智能穿戴等领域得到了广泛的关注。然而,由于振动结构的尺寸缩小到微观尺度,其峰值频率往往依赖于驱动力幅值,大大降低了谐振检测精度,此外,谐振加速度计的灵敏度提升和信噪比改善也一直是微谐振传感领域重点关注的问题。本文通过引入调节电极来减小谐振梁的弯曲刚度,并提出了一种新的高灵敏度加速度测量方案。随着控制电压的增加,谐振式加速度计的灵敏度可以得到提高,突破了单晶硅尺度对谐振式加速度计灵敏度的限制。此外,控制电压对谐振梁的刚度软化作用在提高谐振加速度计的信噪比和克服几何非线性的刚度硬化效应方面也起到了积极作用。图1描述了多电极分布式激励MEMS谐振加速度的结构设计方案,包括一个敏感谐振结构,用于驱动、调节和传感敏感结构的四个分布电极,以及一个可移动的集中质量块,敏感谐振结构两端分别与锚点和集中质量连接。当施加加速度信号时,集中质量可以沿着谐振梁的轴向方向运动,其产生的惯性力作用在敏感谐振梁上。然后,通过测试惯性力诱导的谐振梁频率变化,可以实现加速度信号的感知。图2给出了加速度检测的具体实验方案,将加速度计置于0、30度、-30度、90度、-90度平面时,可以分别产生0g、0.5g、-0.5g、1g、-1g的加速度信号,通过开环测量谐振加速度计的响应频率实现了加速度计的灵敏度标定。实验结果表明,基于谐振梁的前三阶弯曲模态,加速度信号检测的灵敏度分别为85 Hz/g、134 Hz/g和135Hz/g。
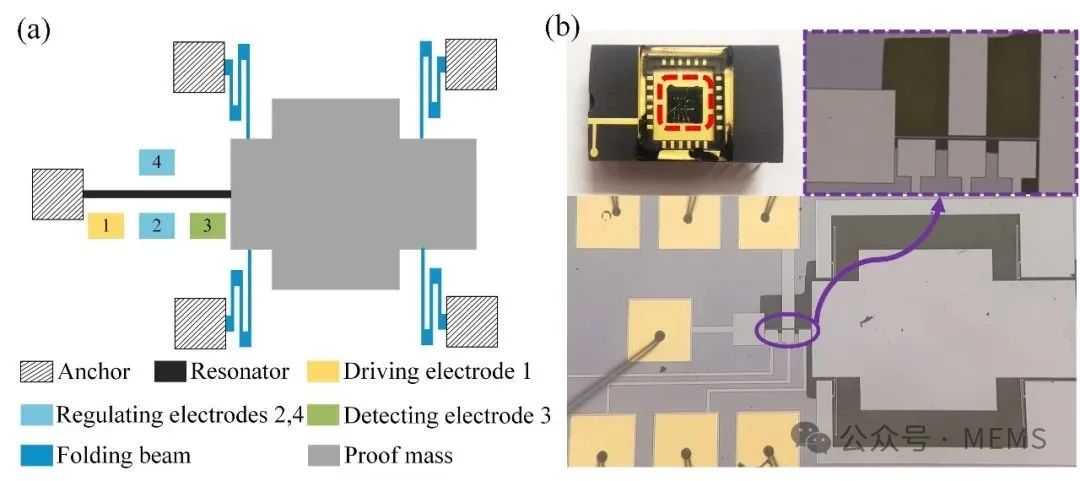
Fig.1 (a) Structure diagram of distributed electrostatically driven MEMS resonant accelerometer; (b) Optical diagram and package diagram of micro-resonant accelerometer
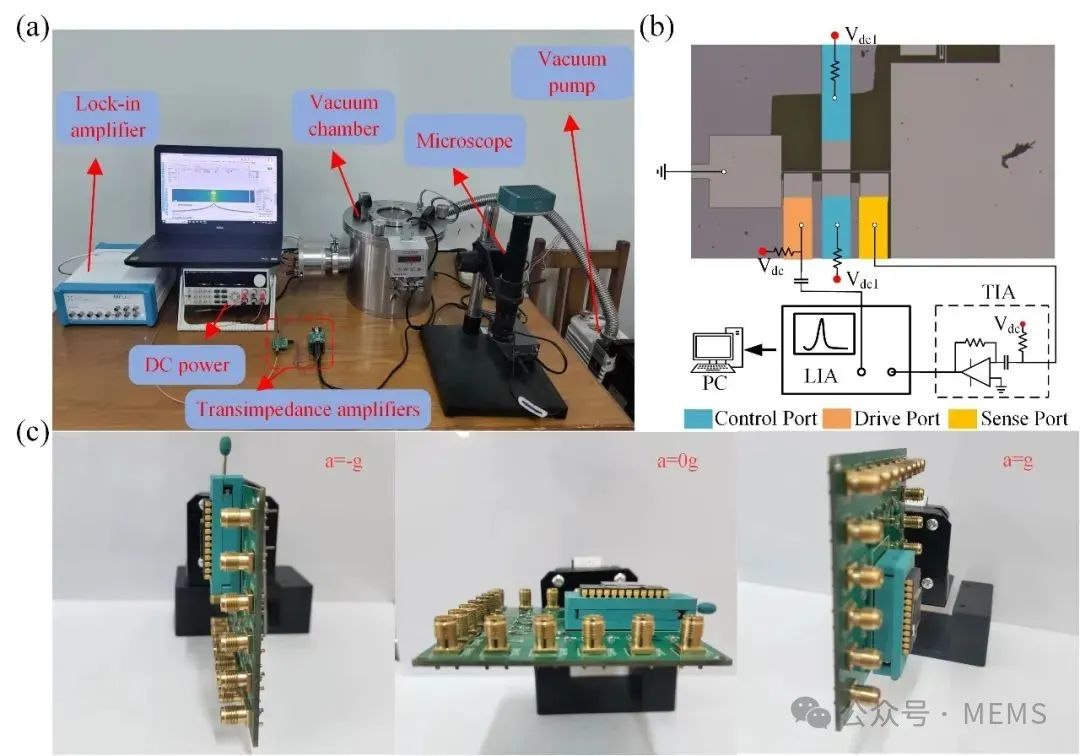
Fig. 2 (a) MEMS resonant accelerometer experimental device diagram; (b) Open loop frequency response measurement setup of the accelerometer. (c) Different placement forms of resonant accelerometer.
根据作者之前的研究结果,随着控制电压的不断增加,谐振梁将达到屈曲状态,使谐振梁由单稳态转变为双稳态。为了进一步提高谐振加速度计的灵敏度,本文提出利用谐振梁的临界屈曲点进行检测。图3 (a)显示当控制电压达到128.8V时,谐振梁的第一阶固有频率降至0,并达到临界屈曲状态。当正向加速信号作用于谐振加速度计时,谐振梁处于双稳态工作范围,随着加速度信号的增强,谐振梁的固有频率增加,灵敏度约为90Hz/g。同样,当负加速度信号作用于谐振梁时,谐振梁处于单稳态工作区间,随着加速度信号的增大,谐振梁的固有频率显著增大,灵敏度达到4984Hz/g,如图3 (b)所示。
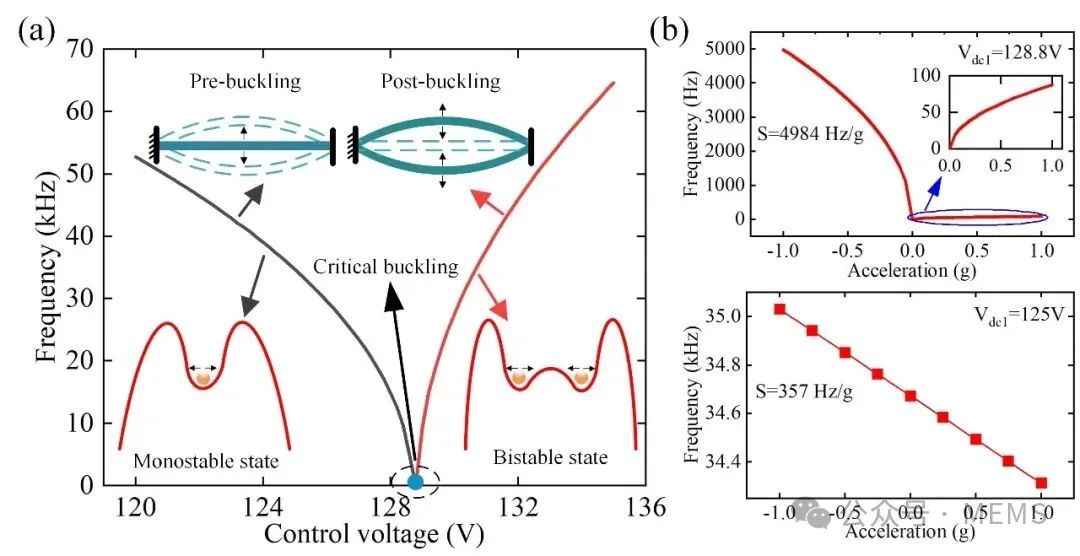
Fig.3 (a) The fundamental frequency of the resonant beam varies with the control voltage before and after buckling; (b) Effect of acceleration on fundamental frequency of resonant beam when the control voltages are 128.8V and 125V.
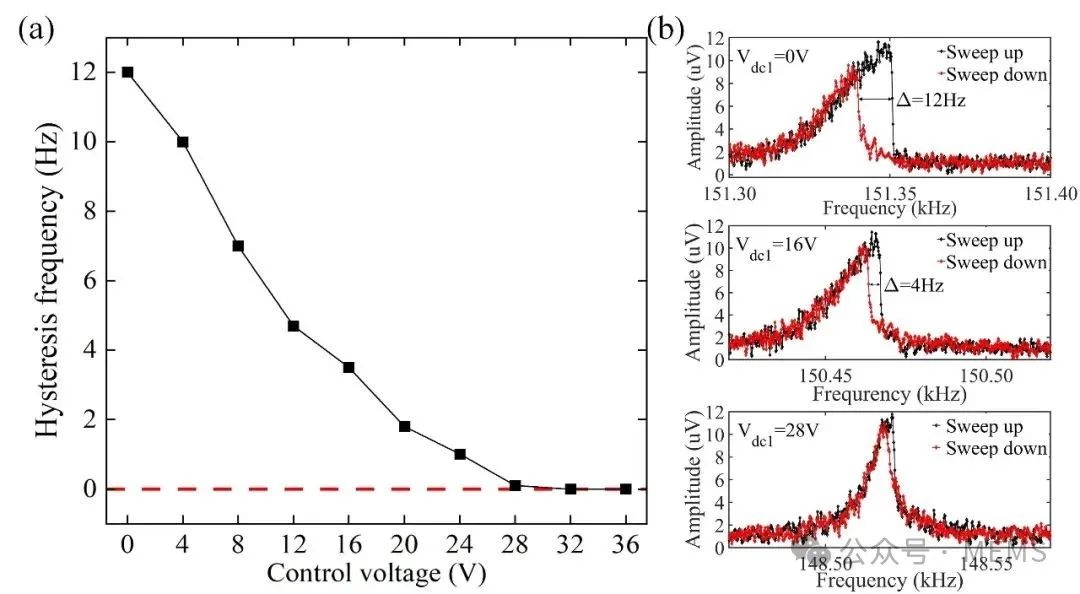
Fig. 4 (a) The influence of control voltage on hysteresis frequency under the same response amplitude; (b) Amplitude-frequency characteristics of the acceleration when the control voltage is 0V, 16V and 28V at 0 g.
由于几何非线性,谐振梁存在明显的刚度硬化,导致了正向扫描峰值频率与反向扫描峰值频率之间存在迟滞,并造成峰值频率对驱动力的依赖性。本文实验研究了控制电压对谐振梁非线性振动行为的影响,结果显示当谐振梁的响应幅值相同时,随着控制电压的增加,第一阶振动的迟滞频率明显减小,如图4(a)所示。例如,考虑谐振梁的响应电压约为12uV,当控制电压增加到28V时,谐振梁的迟滞频率基本变为0,如图4(b)所示。因此,调节电极的引入可以克服由几何非线性引起的谐振检测误差。


