帮帮我，傅里叶先生

一、前言

  前两天，通过实验对比了普通的PWM信号以及 UART发送的PDM信号，经过RC低通滤波之后的交流信号的大小 普通的PWM波形经过 RC低通滤波之后，所存在的交流信号 在占空比为 50% 的时候，达到最大。而使用 串口输出的占空比可调的信号，低通滤波之后的交流分量则呈现一种比较奇怪的分布。

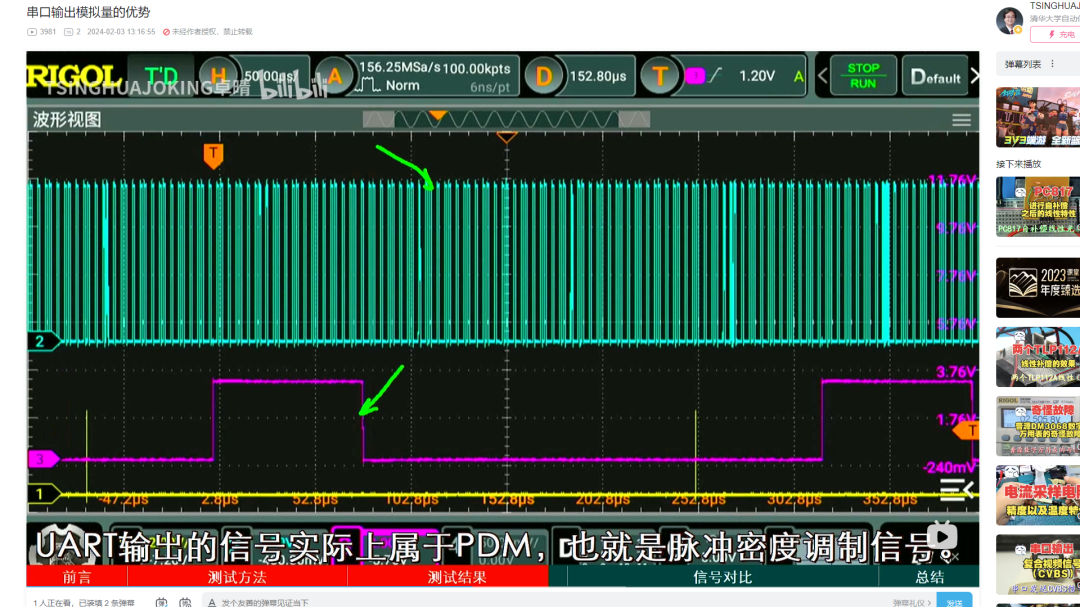
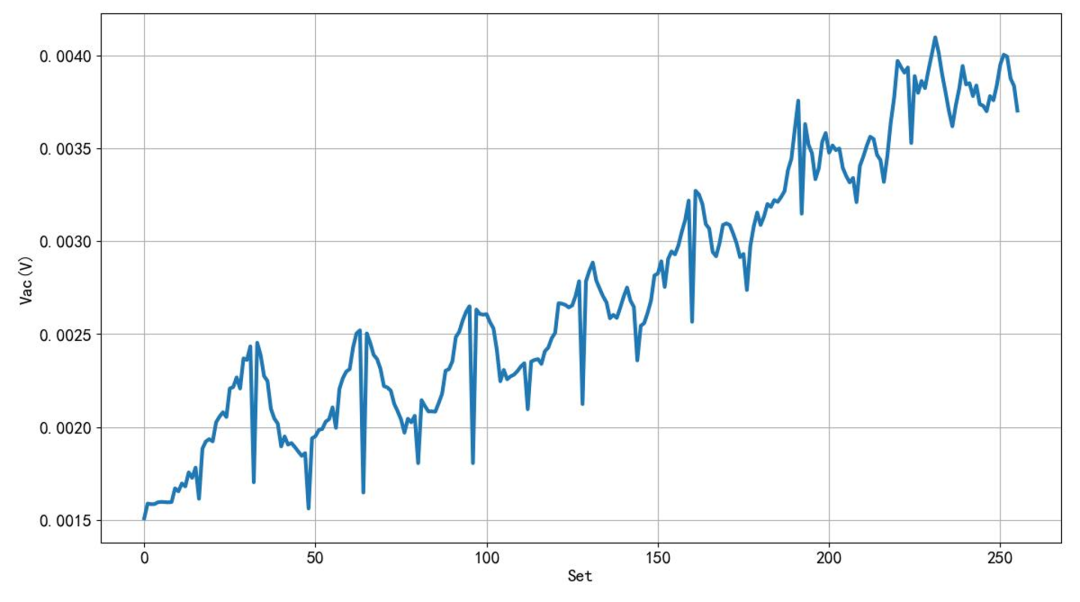
首先，比起普通的 PWM波形来讲，串口输出的信号低通滤波之后的交流分量要小得多。但它随着占空比从 0 到 100% 的变化过程中，这种奇怪的电压变化令人感到疑惑。那么问题来了，这个使用 数字万用表DM3068实际测量单片机发送信号的交流分量曲线，哪些是理论上可以计算出来的，哪些是测量误差造成的呢？下面，就是应用信号与系统理论来解释这个问题的时候了。

二、理论分析

1、电路分析

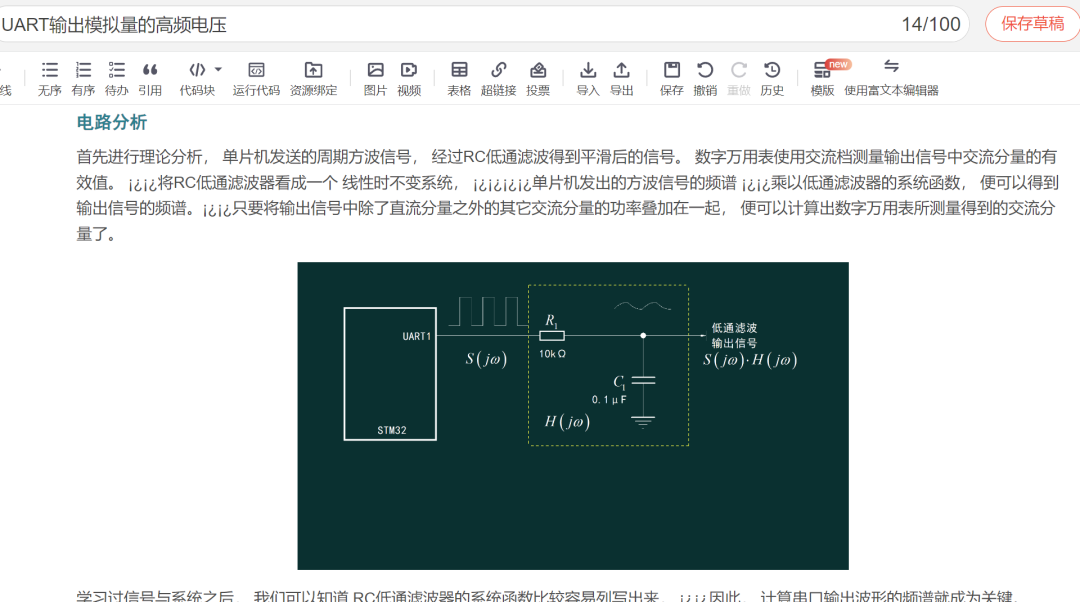
  首先进行理论分析，单片机发送的周期方波信号，经过RC低通滤波得到平滑后的信号。数字万用表使用交流档测量输出信号中交流分量的有效值。将RC低通滤波器看成一个 线性时不变系统， 单片机发出的方波信号的频谱乘以低通滤波器的系统函数，便可以得到输出信号的频谱。只要将输出信号中除了直流分量之外的其它交流分量的功率叠加在一起，便可以计算出数字万用表所测量得到的交流分量了。

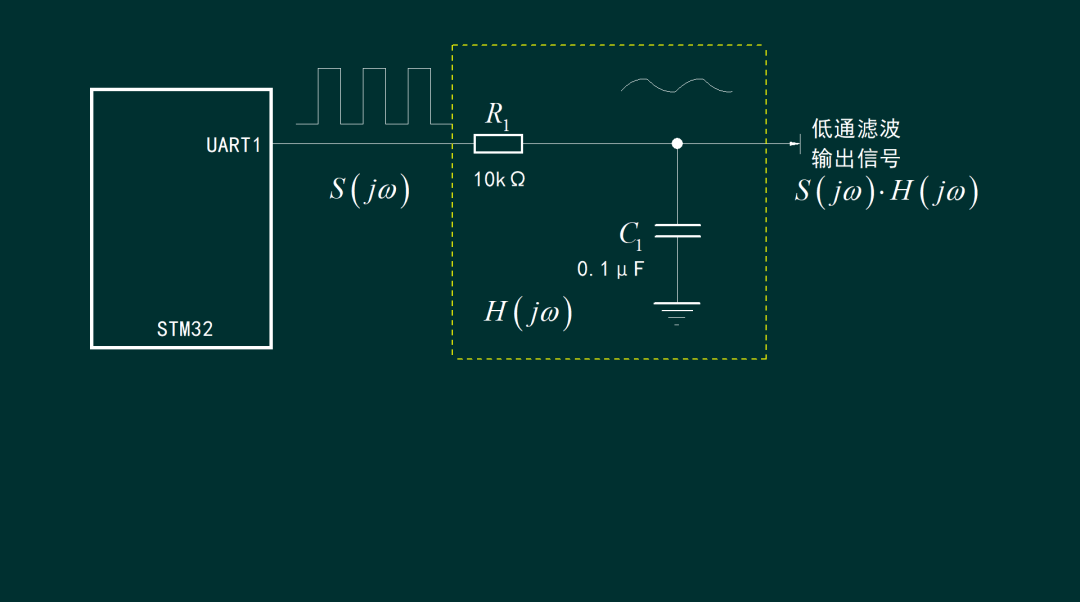
  学习过信号与系统之后，我们可以知道 RC低通滤波器的系统函数比较容易列写出来，因此，计算串口输出波形的频谱就成为关键。下面让我们讨论一下由串口输出的占空比可调的方波信号的频谱。

2、输出信号频谱

  这是串口输出的PWM信号，随着占空比增加，其中为高电平的比特位数也增加了。高电平的位数均匀分布在32个字节中的 256位中。这是占空比为25%的信号，它是由不同的方波信号叠加而成。如果我们知道在任何一个时间位置上的脉冲的频谱，只要将所有脉冲频谱叠加在一起，便可以得到该信号的频谱了。下面就按照这个思路进行分析。

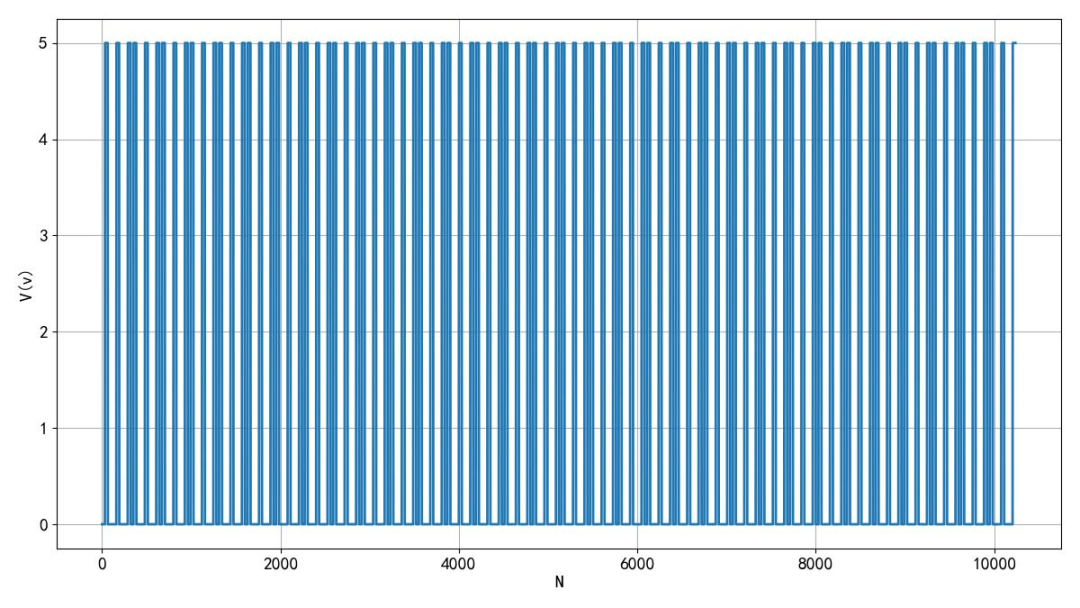
  一切都从这个高度为 E，宽度为 tao 的脉冲信号讲起，它的频谱是一个对称的sinc函数，  如果将它平移到 t0，那么对应的频谱 就只要在后面乘以一个相位因子。下面就可以把 串口输出信号中所有脉冲的频谱加在一起了。

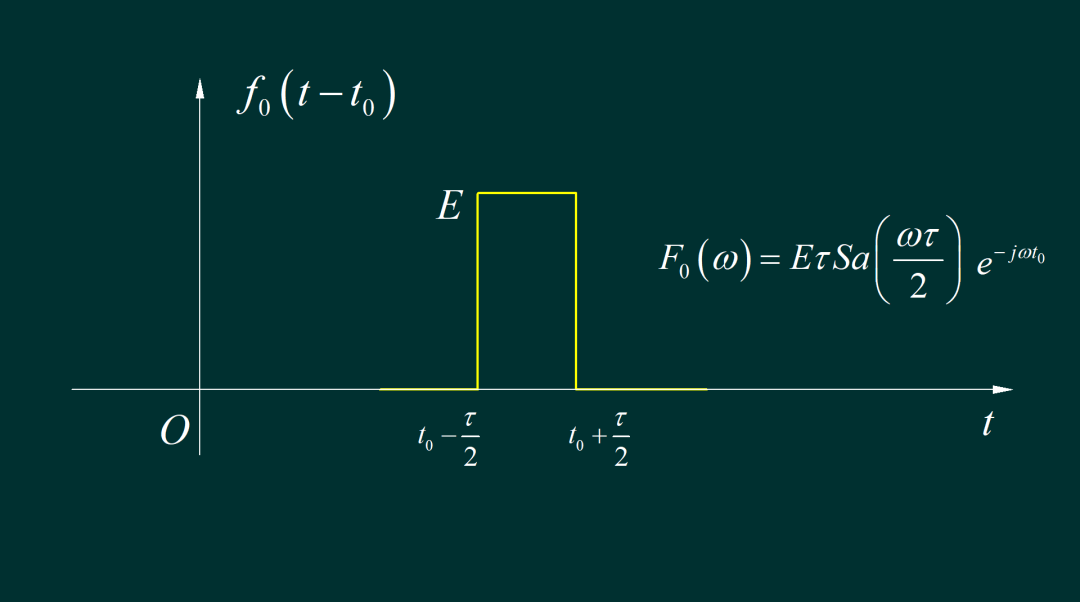
  使用 x[n] 表示 串口输出信号对应位的数值，1 表示有脉冲，0 表示没有脉冲。32个字节总共包括有 256个数据位，32个起始位和32个停止位。将它们的频谱分别计算出来，然后乘以 x[n] 进行叠加，这样就得到了输出信号的频谱。请注意，串口输出的是一个周期为 32个字节对应的周期信号，它的频谱是离散频谱，在上面计算得到的基础上，进行离散化而得。 最后，我们便得到了串口输出信号的实际频谱了。其中的 E 是3.3V电平，tao 是每一比特对应的时间，为1微秒。将这个频谱乘以 RC 低通滤波器的系统函数之后，再把所有交流分量叠加在一起，便可以计算出数字万用表所测量到的交流分量的大小了。

三、仿真结果

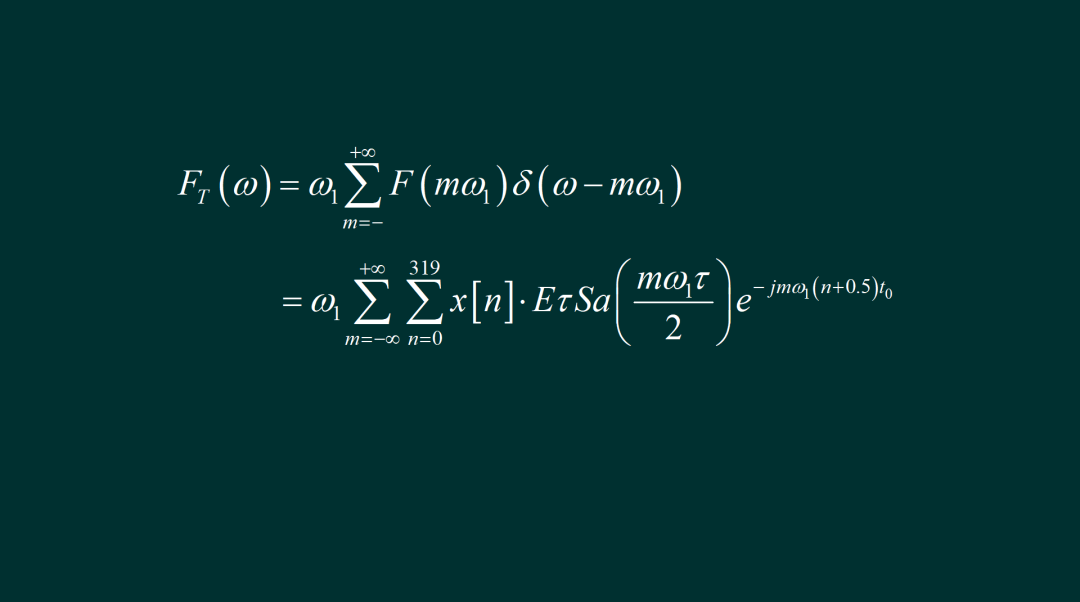
  有了理论分析之后，下面就是通过 Python 编程，分别计算输出占空比从 0 到 100%的过程中，串口信号滤波后交流分量的大小了。这是计算出来的结果。果然不出所料。可以看出与实际测量的结果挺像的。看看这些细节部分，原来以为是测量噪声，现在看来实际上就是这个样子。另外一个与测量结果不同的是，输出交流信号的大小是关于占空比50% 左右对称的。对比数字万用表实际测量的结果，输出交流分量则是随着占空比的增加而逐步上升。这一点是与理论分析不符合的。通过理论分析，让我们知道了测量结果中哪些是真实的，哪些是测量误差。

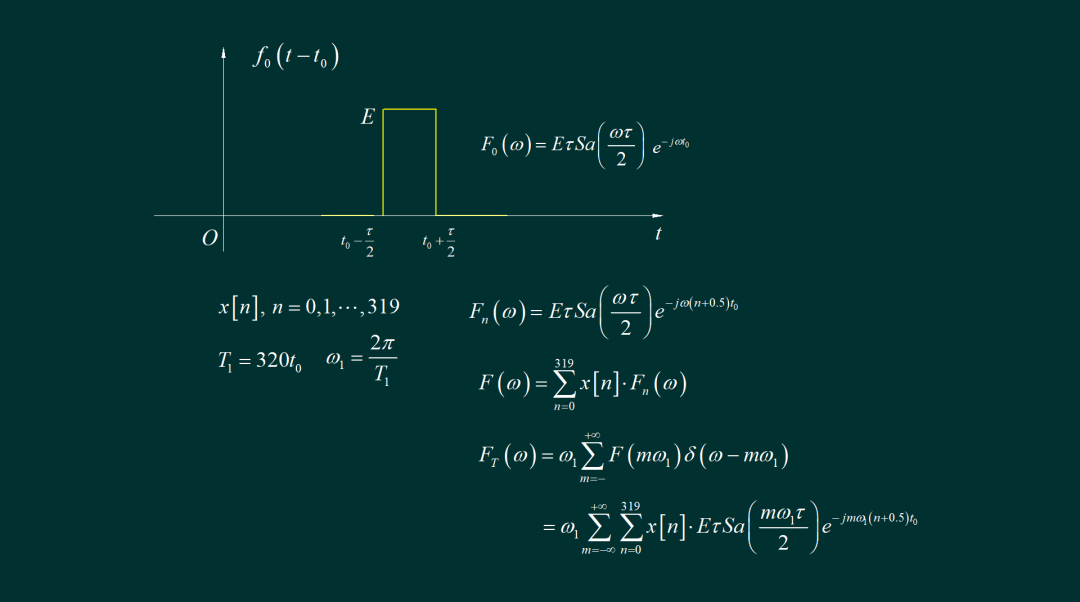
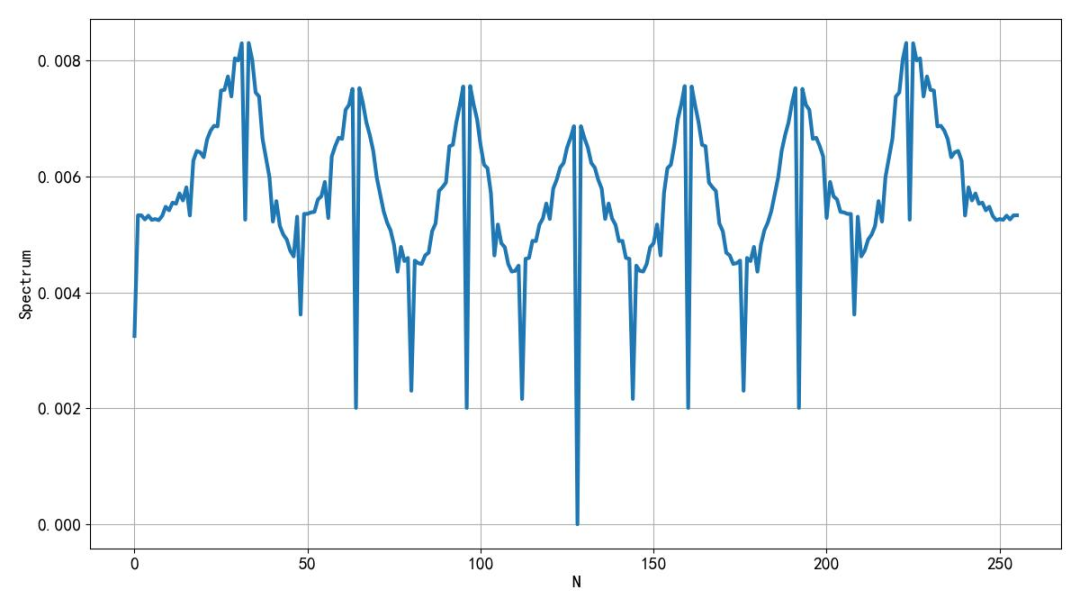
#!/usr/local/bin/python
# -*- coding: gbk -*-
#******************************
# TEST1.PY                   - by Dr. ZhuoQing 2024-02-07
#
# Note:
#******************************

from headm import *

#------------------------------------------------------------

BYTE_NUM = 32
buf = bytes([0]*BYTE_NUM)
bitbuf = [0]*(10*BYTE_NUM)

def Buf2BitBuffer():
    global bitbuf, buf

    id = 0
    for b in buf:
        bitbuf[id] = 0
        id += 1

        for i in range(8):
            if b & (1<<(7-i)): bitbuf[id] = 1
            else: bitbuf[id] = 0
            id += 1

        bitbuf[id] = 1
        id += 1


#    for i in range(len(bitbuf)):
#        bitbuf[i] = 0

#    for i in range(32):
#        bitbuf[i] = 1


#------------------------------------------------------------
Buf2BitBuffer()


#------------------------------------------------------------
bits = 1e-6
T = bits * (10 * BYTE_NUM)
printf(T)
tao = bits
OMEGA = 2*pi/T
E = 3.3

#------------------------------------------------------------
FREQUENCY_NUM = 50
fbuf = [0]*FREQUENCY_NUM

R = 10e3
C = 0.1e-6


def BitBuffer2Frequency():
    global bitbuf,fbuf

    for i in range(len(fbuf)):
        fbuf[i] = 0

    for id,b in enumerate(bitbuf):
        shiftt = id*tao+tao/2

        if b == 0: continue

        for iidd,f in enumerate(fbuf):
            omega = 2*pi*iidd / T

            a = omega*tao/2
            if a == 0:
                fv = tao
            else: fv = tao * sin(a)/a

            fv *= exp(-1j * omega * shiftt)

            a = 1/(1+1j*omega*R*C)

            fbuf[iidd] += fv*a*OMEGA*E



    fbuf[0] = 0


#------------------------------------------------------------

def ACenerge():
    global fbuf
    return sqrt(sum([abs(f)**2 for f in fbuf]))


def SetDACBuffer(dac):
    global buf
    count = 0

    blist = []
    for i in range(BYTE_NUM):
        b = 0
        for j in range(8):
#            count += 1
#            if count < dac:
#                b |= (0x80>01 >j)

            count += dac

            if count >= 0x100:
                count -= 0x100
                b |= (1<
        blist.append(b)

    buf = bytes(blist)

#------------------------------------------------------------

def ShowBitBuffer(drawflag = 0):
    global bitbuf

    bitcurve = []
    BIT_LENGTH = 32

    for b in bitbuf:
        if b == 0: bitcurve.extend([0]*BIT_LENGTH)
        else: bitcurve.extend([5]*BIT_LENGTH)


    plt.clf()
    plt.plot(bitcurve, lw=2)

    plt.xlabel("N")
    plt.ylabel("V(v)")
    plt.grid(True)
    plt.tight_layout()

    if drawflag == 0:
        plt.draw()
        plt.pause(.001)
    else:
        plt.show()


#------------------------------------------------------------
'''
plt.draw()
plt.pause(.001)

for i in range(0x100):

    SetDACBuffer(i)
    Buf2BitBuffer()
    ShowBitBuffer()

    pltgif.append(plt)

pltgif.save()

exit()

'''
#------------------------------------------------------------

SetDACBuffer(0x40)
Buf2BitBuffer()
ShowBitBuffer(1)





exit()

#------------------------------------------------------------

ACDim = []
for i in range(BYTE_NUM*8):
    printf(i)
    SetDACBuffer(i)
    Buf2BitBuffer()
    BitBuffer2Frequency()
#    printf(bitbuf)
    ACDim.append(ACenerge())

#------------------------------------------------------------



printf(ACDim)


plt.plot(ACDim, lw=3)
#plt.plot(bitbuf, lw=3)

plt.xlabel("N")
plt.ylabel("Spectrum")
plt.grid(True)
plt.tight_layout()
plt.show()

#------------------------------------------------------------
#        END OF FILE : TEST1.PY
#******************************

※ 总  结 ※

  本文分析了串口输出的PWM波形低通滤波后的交流分量，Python仿真程序可以在 CSDN博文中找到。这里应用了信号的傅里叶分析的数学工具。回答了看似奇怪测量结果中的现象。这个过程比较有趣，可以在来年春季学期的信号与系统课程中，当做一个实验作业请同学们进行练习。