短波红外在光学遥感应用中发挥重要作用,调制传递函数在轨测试是评价短波红外相机成像质量的重要手段。理论上基于倾斜刃边法的在轨测试方法主要用于可见光波段高分辨率相机,选择采样区域的自由度相对较大。短波红外相机受限于探测器水平,其采样区域受到小像素阵列、低像元分辨率的限制,可供选择的采样区域受限。地物目标在短波红外波段表现出独特的图像特征,可供选择的刃边图像与其他波段存在明显差异,适用于其他波段的采样区域在短波红外波段存在失效的可能。
据麦姆斯咨询报道,近期,中国电子科技集团公司第五十四研究所与河北省光子信息技术与应用重点实验室的科研团队在《激光与光电子学进展》期刊上发表了以“短波红外相机调制传递函数在轨测试”为主题的文章。该文章第一作者和通讯作者为王伟。
本文将倾斜刃边法应用到短波红外波段,分析调制传递函数对于评价成像质量的全面性。通过推导边缘扩散函数、线扩散函数、调制传递函数之间的关系,分析倾斜刃边法的基本原理和流程。最后基于商业卫星短波红外相机载荷,选取短波红外遥感影像地物目标,计算沿轨和垂轨方向全频率调制传递函数,并对结果进行分析说明。
傅里叶光学中定义点扩散函数(PSF)表征光学系统对点目标的输出光场分布,数学上表示为光学系统对脉冲函数的脉冲响应。对于线性空间不变非相干光学成像系统,成像过程为物方点源目标经光学系统作用后像空间光强的线性叠加,数学上表示为物方目标与点扩散函数的卷积。
遥感相机实际在轨成像过程中,大气信道衰减、加工装调误差、冲击振动、探测器噪声等因素都会造成图像对比度的恶化,从而导致调制传递函数的降低。由于各影响因素之间相互独立,光学遥感相机调制传递函数是成像过程各环节扩散函数或调制函数的累积,可以全面地表征相机成像质量,其在轨测试具有重要参考价值。
基于刃边法的在轨MTF测试方法
倾斜刃边法提取单一倾斜刃边图像计算调制传递函数,刃边目标可以分解为点目标与线性目标的几何变换:理想点目标是二维空间冲激函数,沿指定路径移动形成线性目标。相机对线性目标的响应即为线扩散函数(LSF),可表示为点扩散函数沿特定路径的积分,对线扩散函数的傅里叶变换取模即可得到光学相机调制传递函数。基于倾斜刃边的调制传递函数标校流程如图1所示。
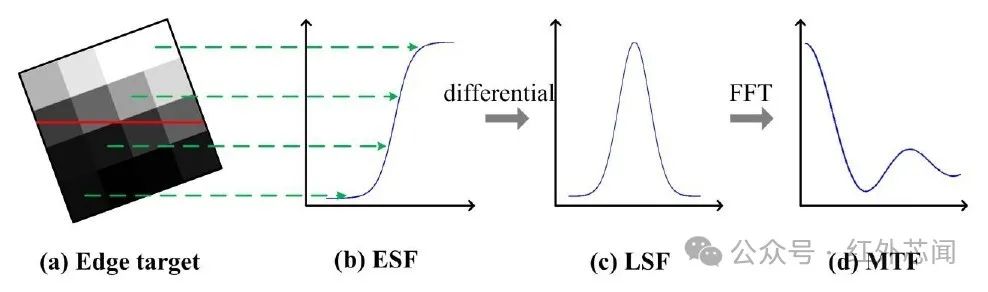
图1 调制传递函数在轨测试流程
本文涉及的短波红外相机是长光卫星技术股份有限公司“吉林一号”卫星星座光谱01~02系列卫星有效载荷之一,相关指标参数如表1所示。短波红外相机采用小规格、大像元分辨率非制冷型焦平面探测阵列,采用焦面滤光片分光的方式提供1000 nm ~ 1700 nm波段范围内四通道短波红外影像,地面像元分辨率约为100 m。


图2 短波红外遥感影像采样区域示意图
短波红外相机在轨测试
选定倾斜刃边图像后,首先确定刃边边缘位置。为降低图像分辨率对刃边边缘提取精度的影响,采用三次样条插值模拟刃边明暗色阶的平滑过渡,以增加采样点获取亚像素级边缘。对扩充后的刃边色阶灰度值进行最小二乘拟合并计算拟合曲线的二阶导数,灰度变化最大即二阶导数为零的点即为刃边边缘位置。对像素阵列每一行的刃边边缘位置进行线性拟合既可得到刃边边缘模型,上述过程如图3所示。
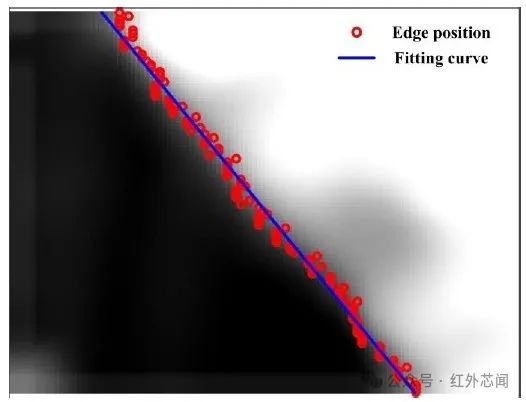
图3 提取倾斜刃边边缘示意图
以刃边边缘模型为基准,将边缘两侧像素沿拟合直线的方向投影,按照灰度梯度变化配准数据点并绘制散点图,拟合散点图以确定边缘扩散函数。多项式拟合和Fermi拟合是常用的拟合方法,图4所示为多项式拟合和三阶Fermi拟合对比。

图4 边缘扩散函数多项式拟合和Fermi拟合对比曲线
对边缘扩散函数微分得到的归一化线扩散函数如图5所示。在图2所示的影像中沿垂轨方向和轨方向各采集两幅刃边图像,按照前述流程计算调制传递函数,各采样区域数据统计如图6和表2所示。

图5 (a)归一化线扩散函数和(b)归一化调制传递函数示意图

图6 归一化调制传递函数曲线
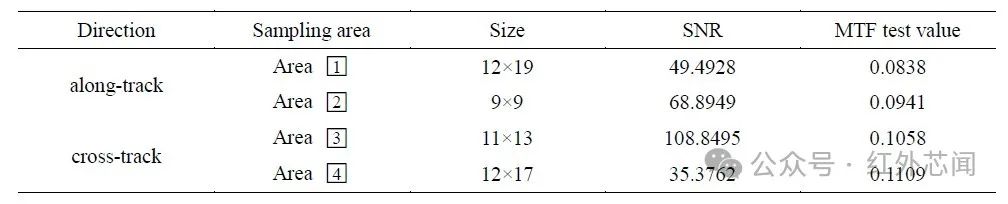
采用倾斜刃边法时,应选择面积尽可能大、明暗边界清晰的地物目标以降低配准误差,短波红外相机分辨率限制了可供选择的地物目标,地物目标的非均匀性辐射与探测器非均匀性响应均会引入计算误差,因此需要对影像数据进行多次采样筛选出结果较为稳定的区域。
针对短波红外相机像质评估,将倾斜刃边法引入短波红外波段,在傅里叶光学基础上分析说明基于倾斜刃边的调制传递函数在轨测试原理。选择短波红外遥感影像中的地物目标对该方法进行验证,奈奎斯特频率处相机调制传递函数在0.0838~0.1109之间。试验结果表明,对于地面像元分辨率严重受限于探测器的短波红外相机,倾斜刃边法在轨测试依然有效,具有工程实用价值。进一步建立完整的遥感相机在轨调制传递函数模型是重要研究方向,对评估遥感相机设计、提升在轨测试精度具有重要意义。
DOI: 10.3788/LOP232235
延伸阅读:
《新兴图像传感器技术及市场-2024版》
《光谱成像市场和趋势-2022版》


