这篇文章我将告诉大家如何用复数法来分析谐振电路,LC谐振电路它的特点是使电路在特定频率下的幅值产生较大的变化,LC谐振电路如下图所示:
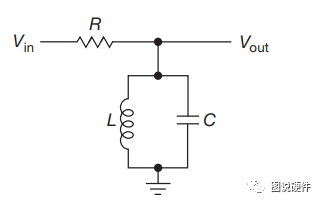
我们来计算LC部分的阻抗:
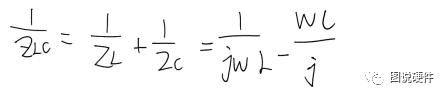
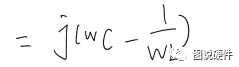
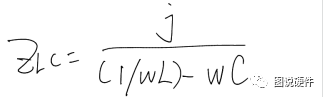
电阻在此电路中,起分压的作用,当频率为:
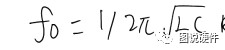
此时频率下的ZLC无穷大,所以此LC电路的响应如下图所示:
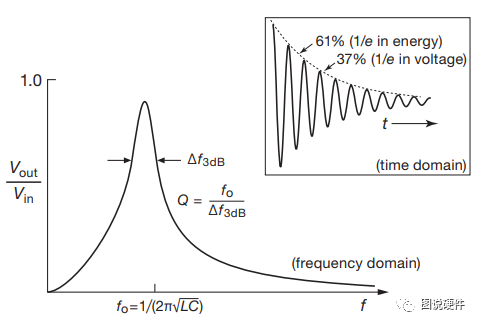
当我们输入一个方波时,通过傅里叶变换我们知道脉冲包含了许多其他频率,所以LC会在相应频率下将阻抗变化为无穷大,而其他频率点的阻抗偏小,所以在上升沿的一瞬间可以看到电压在某一频率下震荡起来,而这一频率往往就是fo,但是大家在实际测量中可能会发现电感与电容的寄生参数会影响到谐振频率。
电感的质量因数Q会影响谐振频率:
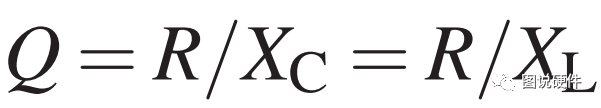
除了以上介绍的并联式RCL谐振,还有一种串联RCL谐振,如下图所示:
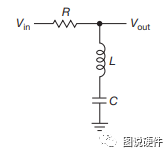
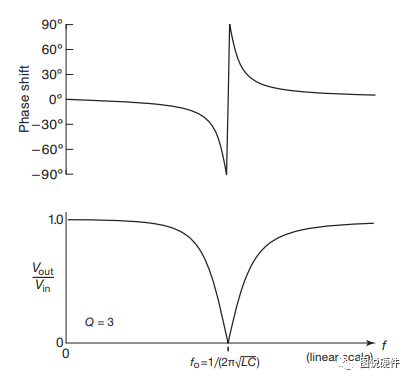
通过以上串联方式的RCL电路的阻抗公式,你会发现在谐振RLC电路阻抗为0,但是在现实中由于寄生参数的存在 VOUT/VIN不会在谐振频率上完全为0,下图为质量因数=3时 VOUT/VIN的曲线,此类谐振电路一般应用于射频电路中,值得一提的是串联LCR谐振电路的电压和电流之间的相位会在谐振点附近发生反转(感兴趣的同学可以通过阻抗法推导得知),如下图所示:
看完RLC谐振电路我们可以再来看一下LC滤波电路,由于LC滤波器是二阶滤波器所以它的效果比普通RC电路好很多,如下图所示:
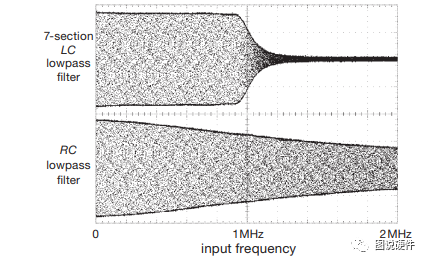
阴影部分是通过滤波器的波形,横坐标是频率,我们可以看到二阶滤波器比一阶滤波器好太多了。
本片短文到此为止,如果你喜欢的话,可以点赞分享收藏给你的朋友。如果你觉得本篇文章有哪里说的不好或者不对的,可以在评论区指出或者发私信告诉我,谢谢。