在高频信号下，很多器件失去了原有的特性，如我们经常听到的“高频时电阻不再是电阻，电容不再是电容”，这是咋回事呢？那就看今天的文章吧！
容抗的概念
电容有两个重要特性，一个是隔直通交，另一个是电容电压不能突变，先来看一下百度百科对容抗的解释。
简单说，虽然交流电能通过电容，但是不同频率的交流电和不同容值的电容，通过时的阻碍是不一样的，把这种阻碍称之为容抗。
容抗与电容和频率的大小成反比，也就是说，在相同频率下，电容越大，容抗越小；在相同电容下，频率越高，容抗越小。
如何理解容抗与电容大小和频率成反比呢？
以RC一阶低通滤波器举例。
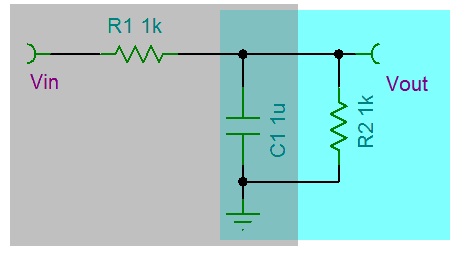
Vin通过R1电阻对电容C1进行充电，Vin的电势加在电容C的两个金属极板上，正负电荷在电势差作用下分别向电容的两个极板聚集而形成电场，这称「充电」过程。
若将Vin拿掉，在Vout上加一个负载R2（青色部分），电容两端的电荷会在电势差下向负载流走，这称为「放电」过程。（流过电容的电流并不是真正穿过了极板的绝缘介质，指的是外部的电流）
衡量电容充电的电荷数为Q，Q=CV，其中C是常量，所以电荷数和电压呈正比。
C=Q/V，电容量代表了电容储存电荷的能力，微分表达式为：
电流是单位时间内电荷数的变化量:
结合(1)和(2)两个公式可得到：
从公式可以看出：电容上的电流和电压的变化量成正比，或者说电容上电压的变化量和电流是成正比的。
即在电压一定时，电容越大，单位时间内电路中充、放电移动的电荷量越大，电流越大，所以电容对交变电流的阻碍作用越小，即容抗越小。
在交变电流的电压一定时，交变电流的频率越高，电路中充、放电越频繁，单位时间内电荷移动速率越大，电流越大，电容对交变电流的阻碍作用越小，即容抗越小。
容抗用 表示，公式如下，其中 是频率， 是容值
因为（ ），所以容抗也可以用如下的公式表示：
感抗的概念
感抗与电感的大小和频率成正比，也就是说，在相同频率下，电感越大，感抗越大；在相同电感下，频率越大，感抗越大。
感抗用 表示，公式如下，其中 是信号频率， 是感值
因为（ ），所以感抗的公式可以用如下表示：
感抗和容抗又被称为电抗，电路的总的阻抗Z由电阻R和电抗X组成。
掌握了预备知识，我们再来看电阻、电容和电感的实际等效模型。
理想的电阻、电容和电感就是如下的这样子，在实际中并不存在，电阻里面会有寄生电容和寄生电感在，在电容里面会有寄生电阻和寄生电感的存在，在电感里面有寄生电阻和寄生电容。
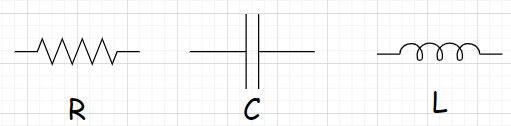
理想电阻器
理想电阻的阻抗即为阻值R：
电阻实际等效模型
电阻上会存在寄生并联电容C寄生串联电感L的存在。
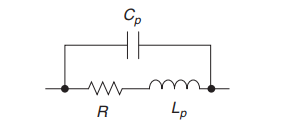
根据上图可得电阻的实际等效阻抗为：
化简可得：
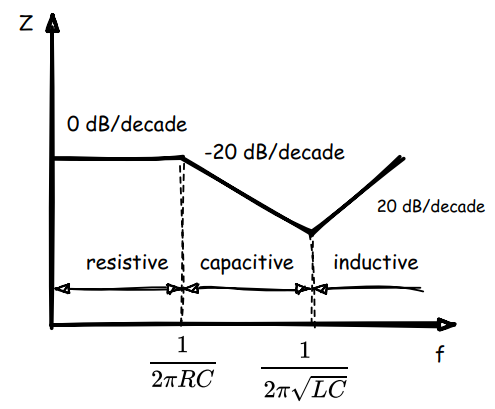
实际电阻器的阻抗和频率曲线，有两个节点，分别为 和 频率小于 时，呈现电阻特性，在 和 之间，呈现电容减少阻抗，频率大于 ，呈现电感增加阻抗的特性。
f1和f2分别对应RC滤波器的截止频率点和容抗和感抗相等时的频率点。
理想电容器
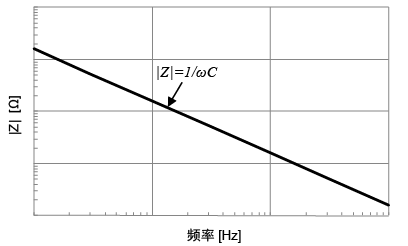
理想电容器阻抗如下图所示，和频率呈反比，随着频率的增加，阻抗逐渐减小，由于理想电容器中无损耗，等效串联电阻ESR为零。
理想电容器的阻抗Z公式为：
电容实际等效模型
理想的电容器在实际中是不存在的，电容的实际模型是一个ESR串联一个ESL，再串联一个电容，ESR是等效串联电阻，ESL是等效串联电感，C是理想的电容。
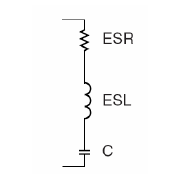
所以上述模型的复阻抗为：
针对以上公式（公式较长，左滑看全部）：
时，电容器表现为容性。
时，电容器表现为感性，因此会有一句话叫高频时电容不再是电容，而呈现为电感，这个电感不是说电容变成了电感，而是指此时的电容拥有了与电感类似的特性。
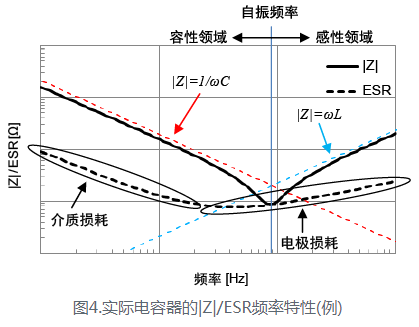
时，此时容抗矢量等于感抗矢量，电容的总阻抗最小，表现为纯电阻特性，此时的f称为电容的自谐振频率。
自谐振频率点是区分电容是容性还是感性的分界点，高于谐振点时，“电容不再是电容”，因此退耦作用将下降。实际电容器都有一定的工作频率范围，在工作频率范围内，电容才具有很好的退耦作用。ESL是电容在高于自谐振频率点之后退耦功能被消弱的根本原因。
下图是实际电容器的频率特性。
理想电感器
理想电感的阻抗为：
电感实际等效模型
电感器的等效模型和电阻是一样的，如下所示：
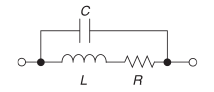
阻抗计算公式和电阻也是一样的，即：
从下图和公式可以看出，理想的电感的阻抗是随着频率的增加而变大的。
等效电感的阻抗图呈一个倒V型，正好和电容相反，倒V的最高点称为电感的自谐振点。
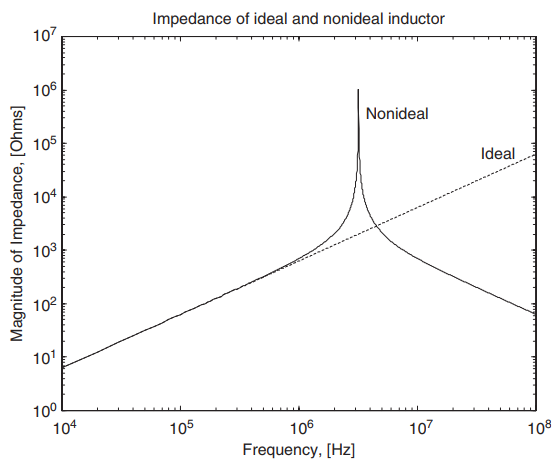
当系统阻尼R提供的衰减不足时，容抗和感抗相互抵消，能量在LC间来回传递，这就是谐振。
电感自谐振频率SRF部分不做过多赘述，在后续的电感选型文章中会重点介绍。
总结
理想的电阻、电容和电感在实际中不存在，都会存在寄生参数，从而在不同的频率下，表现出的特性不同，只有在特定的频率范围内才能发挥出其本身的特性。
今天的文章内容到这里就结束了，希望对你有帮助，我们下一期见，记得点赞/在看/转发哟~
