中国最活跃的射频微波天线雷达微信技术群
电子猎头：帮助电子工程师实现人生价值！
电子元器件：价格比您现有供应商最少降低10%
射频微波天线新产品新技术发布平台：让更多优秀的国产射频微波产品得到最好的宣传！发布产品欢迎联系管理，专刊发布！强力曝光！
麦克斯韦 (James Clerk Maxwell, 1831–1879) 是举世公认的“自牛顿以来世界上最伟大的数学物理学家”，被与其同时代的苏格兰数学家泰特 (Peter G Tait) 誉为：“几乎可以与牛顿比肩的人”。在物理学史上，麦克斯韦具有非常崇高的地位，正如后人所评价的那样，如果我们一定要找出人类历史上十个最伟大的物理学家的话，那么麦克斯韦不仅会以自己的杰出贡献当选，而且还会非常接近最顶尖的位置[1-3]。对于麦克斯韦的功绩，爱因斯坦也曾作了很高的评价，他在1931年纪念麦克斯韦100周年诞辰的文集中写道：“自从牛顿奠定理论物理学的基础以来，物理学公理基础最伟大的变革，是由法拉第和麦克斯韦在电磁现象方面的工作所引起的……这样一次伟大的变革是同法拉第、麦克斯韦和赫兹的名字永远联系在一起的。这次革命的最伟大部分出自麦克斯韦……是牛顿以来，物理学最深刻和最富有成果的工作。”
很显然，麦克斯韦在科学上最伟大的贡献是在电磁学方面。他于1873年出版的《电学和磁学论》一书是集电磁学大成的划时代著作，全面地总结了十九世纪中叶以前对电磁现象的研究成果，并在该书中建立了完整的电磁理论体系。这是一部可以同牛顿的《自然哲学的数学原理》、达尔文的《物种起源》和赖尔的《地质学原理》相媲美的里程碑式的著作。但是这位伟大的科学家由于数学物理基础非常扎实，知识面非常广博，所以其一生在科学的各个领域涉猎甚多，除了电磁学以外，在天体物理、气体分子运动论、热力学、统计物理等方面都做出了开创性的工作。他的贡献如此之多，正如量子论的创立者普朗克所指出的：“麦克斯韦光辉的名字将永远镌刻在经典物理学家的门扉上，永放光芒。从出生地来说，他属于爱丁堡；从个性来说，他属于剑桥大学；从功绩来说，他属于全世界。”
实际上，麦克斯韦在应用力学 (Applied Mechanics) 上也有很多贡献，而其中的某些研究工作已经成为应用力学发展的奠基性成果。由于麦克斯韦作为一名数学物理学家的名气太大，其耀眼的光辉已经大大遮掩了他在应用力学上的贡献，所以很多人甚至大量的力学工作者并不清楚他在力学上有哪些建树。本文从应用力学发展的角度入手，重点考察了麦克斯韦在应用力学研究方面的诸多重要成果。
随着工业和科学技术的发展，应用力学与经典物理学的研究方向逐渐分家。近代应用力学涌现出了若干研究中心，如法国的拉格朗日、拉普拉斯、达朗贝尔、泊松、柯西、纳维叶、圣维南、马略特等人在流体力学、弹性力学、分析力学和天体力学等方面做出了开创性的工作；英国的斯托克斯在流体力学方面提出了N-S方程，雷诺是湍流流动研究的开拓者，泰勒是流体流动稳定性和固体位错研究的开拓者；俄罗斯出现了齐奥尔科夫斯基、茹科夫斯基、查普雷金、谢道福等优秀的力学家。而我国著名的力学家钱学森、张维等人特别推崇近代应用力学的另外一个发源地，即哥廷根大学。近代的哥廷根应用力学学派，以普朗特为首，带动了一大批人致力于将力学应用于工程技术，从工程里面提炼出力学模型，然后上升到理论高度以指导实践。哥廷根学派在上述学术思想的指导下，涌现出了大量的享誉世界的应用力学家，例如铁摩辛柯、冯·卡门、普拉格、邓哈托、那戴、钱学森、钱伟长等。而麦克斯韦既是一位伟大的经典物理学家，又是符合上述应用力学定义的应用力学家，他提出的很多力学理论对于后世解决工程应用问题起到了奠基性作用。
麦克斯韦在应用力学方面的研究涉及到弹性力学、光弹性、结构力学、粘弹性力学、天体力学、流体力学、动力稳定性等方面，后人如果能够在上述任一领域做出其中的一项贡献，便足以名列力学发展的丰碑。具体来说，麦克斯韦在力学上的贡献主要可以归纳为以下几个方面：
在1850年，年仅19岁的麦克斯韦就掌握了当时尚未发展完善的弹性理论，并且发表了一篇题为《论弹性体的平衡》的论文[4]。在该文中，他详细讨论了若干个弹性力学的特殊问题，如三角形的受力问题等。这些问题的精确解大半已为其他学者所解出，但是该文中这些结果是年轻的麦克斯韦独立求得的。通过这篇论文，麦克斯韦初步展示了他突出的数学物理才能，并为其以后的科研打下了基础。此外，麦克斯韦也做了大量的弹性试验，测量了棒与铁丝的弹性系数，并且对水的可压缩性进行了认真思考。
1852年，麦克斯韦提出了光弹性实验的应力–光学定律，即条纹上各点的主应力之差可以表达成
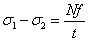
其中，N 为等差线的级数，f 为模型材料的条纹值，t 为模型的厚度。麦克斯韦应用光弹性方法验证了一些弹性力学的解答，结果表明理论解答与实验值非常吻合。所以后人认为麦克斯韦是以光弹性方法实际求解弹性力学应力场的第一人，也是光弹性仪器的实际发明者。到十九世纪末，光弹性方法迅速扩展成为全场测量应力方法的重要手段，在材料、航天、医学、水利、土木等工程领域发挥着巨大作用[5]。
麦克斯韦在结构力学方面的贡献也是很伟大的，他对桁架进行了多年研究，并在1864年进行了总结[6]。这时候，他已经能够对桁架的静定与超静定结构进行区分。对于静定桁架，麦克斯韦在前人的基础上简化了用作图的方式去求桁架的内力，指出桁架的形状和内力图是一对互易图，而该方法也被称为“麦克斯韦力图法”。对于超静定桁架，例如拱和吊桥等结构，麦克斯韦从能量的角度推导出了求解该类超静定结构的一般方法，得到了位移互等定理
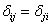
即结构的第一力系在第二力系上引起的弹性位移上所做的功，等于第二力系在第一力系上所引起的弹性位移上所做的功。在此基础上，麦克斯韦又提出了单位载荷法，可以用于求解桁架的位移，即
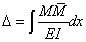
其中，M 和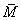
分别为梁上任一截面由于外加载荷和单位力产生的弯矩。上式是莫尔 (O Mohr, 1835–1918) 大约在十年之后进一步整理给出的规范形式，所以该式又称为麦克斯韦–莫尔方法。
1870年麦克斯韦将英国天文学家艾里 (G R Airy, 1801–1892) 提出的弹性力学中的艾里应力函数由二维推广到三维情况，并指出它应满足双调和方程
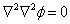
该应力函数
