我们先看看图(1)。
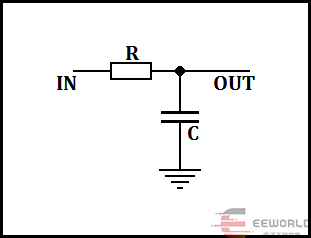
图(1)
这个电路,可以说是最简单的非纯电阻电路,仅有一个电阻和一个电容。
如果输入(IN端)信号是个阶跃函数(某些教材中称亥维赛函数),即时刻零之前电压为零,时刻零之后为1(当然也可以为某个确定的不变数值,这只要乘以一个常数即可),而且电容在时刻零之前没有存储电荷,那么电容两端电压是逐渐上升的。大致如图(2)。
图(2)中,红色曲线是输入信号(阶跃函数),蓝色曲线是输出信号,即电容两端的电压。图中可见,电容两端电压是逐渐上升的,随时间的推移越来越接近输入信号的幅度。数学分析指出,蓝色曲线是一条指数曲线。实际电路中,常用此RC电路实现信号的延迟。如果输入信号是个正弦信号,那么输出信号仍是个正弦信号,但幅度减小,减小多少由电阻的阻值和电容的容抗分压决定。容抗随频率的升高而减少而电阻数值不随频率变化,所以电容两端电压与输入电压的比值随频率升高而减小。
换言之,频率低的信号容易通过这个RC电路,减小得很少,频率高的信号则不容易通过这个RC电路,减小得比较多。所以,这个电路是个低通滤波电路。另外,输出信号与输入信号并不同相,而是落后于输入信号。频率越高,相位落后得越多,最多落后90度。由于该电路的微分方程是一阶微分方程,所以此电路又称一阶低通滤波电路。
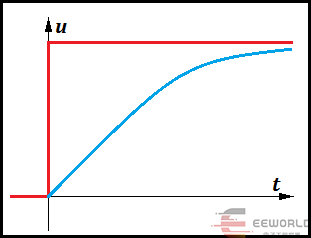
图(2)
该电路中,如果电阻R右端电压上升一个微小数值,例如1毫伏,那么电容中储存的电荷将增加一个微小数值,电荷增加的数值与电容的容量成正比。这是由电容量的定义C=q/u决定的。显然,电容中增加的电荷越多,从电阻方面看过去,电容量就越大。实际电路中,电容量C是不变的,是个常数。
如果我们将电容器原来接地(电压总为零)的一端改接到一个反相放大器的输出端,如图(3),那么会发生什么情况?
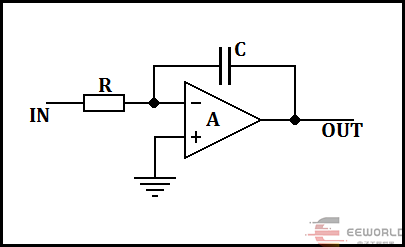
图(3)
假定这个反相放大器的电压放大倍数(电压增益)为A,那么电阻与电容联接处即反相放大器的输入端电压上升一个微小的数值例如1毫伏,那么放大器输出端将下降A毫伏,如果A=100,电容器C的右端将下降100毫伏。我们可以看出来:电容中储存的电荷将增加为图(1)中的99倍,接近100倍。这是因为电容两端电压变化为图(1)中的99倍。
那么从电阻向右看过去,电容器的电容量不是C,而是99C。因为电容器中储存的电荷毕竟是要从电阻流入的。这就好像图(1)中电容变大了,变成了一个容量为99C的电容一样。这种现象,就叫做米勒效应。这个99C的电容当然是虚拟的,是由于反相放大器输出端电压变化而产生的,叫做米勒电容。近似地,可以认为电容器C被放大了反相放大器电压放大倍数那么多倍。如果该电路用于延迟输入信号,那么近似地,延迟时间也将增加到反相放大器电压放大倍数那么多倍。
与图(1)不同的是:图(3)中输出与输入反相。
实际的反相放大电路,例如由双极型三极管构成的共发射极放大电路,或者由MOS管构成的共源极放大电路,如果在集电极与基极之间跨接一个电容,如图(4),由于共发射极放大电路输出与输入反相,从输入端电阻向右看这个电容,同样电容量被近似放大了A倍,A是这个共发射极放大电路的电压放大倍数。
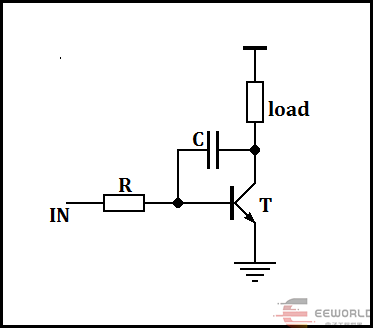
图(4)
双极型三极管共发射极放大电路的电压放大倍数与三极管的特性如三极管的电流放大倍数有关,与负载load有关,等等,所以电容C被放大的倍数也与这些因素有关。
应该注意:即使没有外接电容C,三极管的集电结也存在分布电容。这个集电极到基极的分布电容在共发射极放大电路中同样会被放大A倍,只不过电原理图中没有显示出来罢了。这个被放大了的集电极到基极的分布电容,也叫米勒电容。该电容是影响共发射极放大电路高频特性的重要因素。
如果将图(4)中双极型三极管换成MOS管,因为共源极放大电路是反相放大,漏极与门极信号反相,所以同样存在米勒效应,跨接在漏极与门极之间的电容同样也会被放大A倍,A是MOS管共源极放大电路的电压放大倍数。同样,即使没有外接电容,MOS管的漏极源极之间分布电容也会被放大A倍。这个电原理图中没有显示出来的米勒电容,在开关电源中会产生相当大的影响,限制了开关电源功率开关管的开关速度。图(4)中可以看出:电阻R越小,米勒电容的影响越小。
所以开关电源中总是要求功率开关管的驱动源能够输出足够大的电流,也就是说,要求驱动源近似理想电压源。这样才能够减小米勒电容的影响,使功率开关管有足够的开关速度。
· END ·