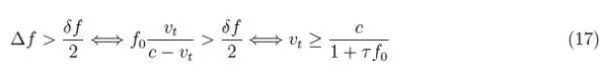航海中常用的声纳是什么原理?是怎样实现导航和测距的?
与使用微波的雷达不同,声纳发射的信号是超声波脉冲,它在海水中的衰减很小。由此,我们可以知道这种设备在水下导航中十分重要。 工作原理
工作原理
总的来说,声纳由潜艇上的发射器和接收器组成。发射器是一个振动电机系统;压电晶体(石英)受到频率为f0的正弦电势差的影响,会以相同的频率产生机械振动。假设f0=21kHz,则会产生一个超声波脉冲,该超声波脉冲一直传播到目标B处,然后被目标B反射。反射的回波将被接收器(麦克风)截获。了解到超声波在海水中的传播速度(c=1500m/s),测量脉冲覆盖返回距离所需的时间Δt,就可以确定发射器与目标之间的距离d,如下所示:
发射器天线具有高度指向性:为了实现360°全景覆盖,天线需绕垂直轴均匀旋转。这样,就可以通过测量正北方向与回波信号传播方向的夹角ρ来确定目标回波的方向。在航海学中,ρ称为极方位,根据目标位置以顺时针(+)或逆时针(-)方向从0°到180°以六十进制进行测量(图1)。通过测量(ρ,d),我们可以获得给定时刻B的位置。如果快速连续重复这些测量,舰载计算机将确定B相对于A的相对速度。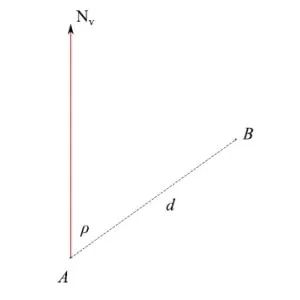 图1:确定目标位置
图1:确定目标位置
 最大距离
最大距离
要确定声纳的最大范围,需要考虑海水对超声波的吸收。具体来说,我们有一个传播波,其时间相关性由持续时间τ的正弦/余弦振荡表示,通常等于1ms: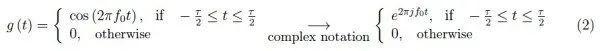
我们假设声纳的发射器在理想情况下是定向的,因此波传播是一维的(沿着发射器原点的x轴)。频率f0对应于波长λ0=cf0-1:因此我们有一个具有指定为λ0的平面波。λ0的唯一性是由石英振荡器的高稳定性保证的。否则,就会出现由函数λ(f)定义的波长范围,其中f属于生成超声波脉冲的振荡器的频带。根据波的传播理论可知,函数λ(f)定义了传播介质的色散定律,如果这个函数不是线性的,就会出现色散现象,脉冲容易变形。因此我们假设λ=λ0。最好将波数k0=2π/λ0,即长度λ0内的完整振荡的数量。由此可见,波的空间部分可写为: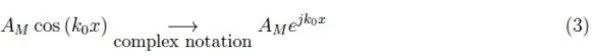
其中AM>0是(恒定)振幅。在存在由水吸收产生的衰减的情况下,振幅在传播过程中趋于减小。我们考虑一个由参数α>0控制的指数衰减,将其称为衰减系数,方程(3)变为:
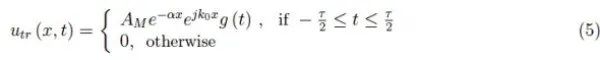
我们说g(t)是一个截断的正弦振荡(图2),并且我们已经从中知道了它的傅里叶频谱(如图3所示)。因此,发射信号的带宽为δf=2/τ=2kHz,发射器发射的不是频率为f0=21kHz的严格的正弦脉冲,而是发射频率范围为f0−δf/2=20kHz~f0+δf/2=22kHz的脉冲。
A上的发射器发射的波到达B并被B反射。如果B相对于A是静止的,则反射过程保留频率和波长,但不保留传播方向,而传播方向可以是以B为中心,在A所确定的追踪半空间内描画的半球中的任何方向。因此,反射脉冲是球面波:
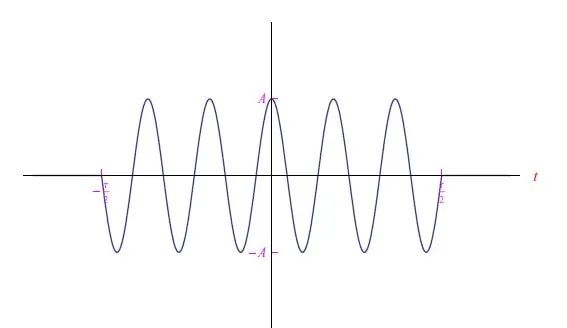 图2:平面波的时间分量(5)
图2:平面波的时间分量(5)
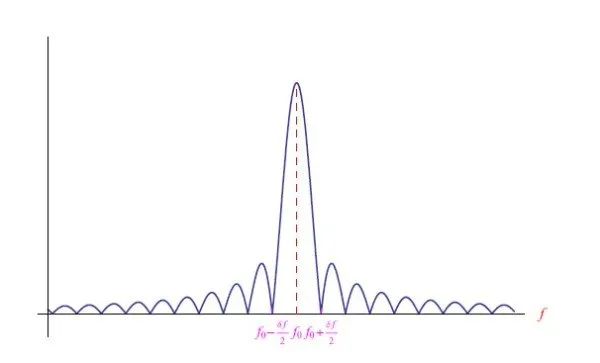 图3:方程(2)的谱密度
图3:方程(2)的谱密度
其中r是空间极坐标系的径向坐标,极点为目标B。如果d是A和B之间的距离,则振幅BM由下式给出:
关于声纳发射的波的传播,最大距离D使得AMexp(−αD)是可以反射的最小振幅。简而言之,当d>D时,波会受到衰减以致不会被反射: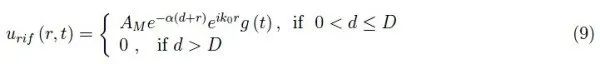
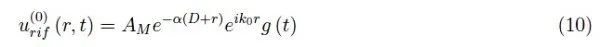
也就是说,如果B位于距离D处,则有反射波。当反射波到达接收器时,我们有r=D: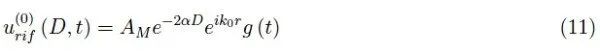
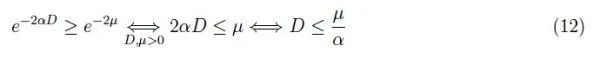

理论示例:典型值为α=10−1m−1,对于µ=104,我们得到D=105m,相当于大约55海里(第一个声纳的最大范围为2,700米)。 脉冲传输频率
脉冲传输频率
现在让我们计算脉冲传输频率,即一个脉冲与下一个脉冲之间的时间间隔T的倒数。为此,我们将来自位于Dmax(公式13)的目标的返回信号称为最远回波。该信号的往返时间由下式给出:
在发送下一个脉冲之前,必须测量最远的回波。所以,我们有:
例如,对于Dmax=105m必须是T>133.3秒。因此我们可以假设T=140s,这对应于频率ν=7.14·10-3Hz。 多普勒频移
多普勒频移
目标的相对速度是通过快速连续测量其位置计算出来的。不过,对利用目标运动造成的反射频率多普勒频移的可能性进行评估是有益的。事实上,反射过程可以理解为B发射脉冲。为此,我们要记住图4中的运动构型,即在A静止的参考系中,B以速度v运动。分量vt被称为横向速度,如果B接近则被视为正值,反之亦然。在这种情况下,反射信号会发生频率偏移:
由此可见,接收器测量的不是f0,而是f0+Δf。然而,当且仅当Δf>δf/2时,多普勒频移Δf是可检测到的,否则f0+Δf落在发射频带内,因此B不一定在移动。图5说明了先前的情况。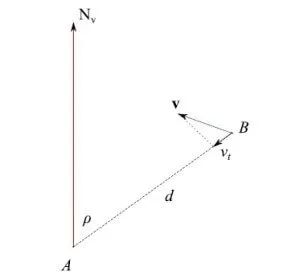 图4:横向速度
图4:横向速度
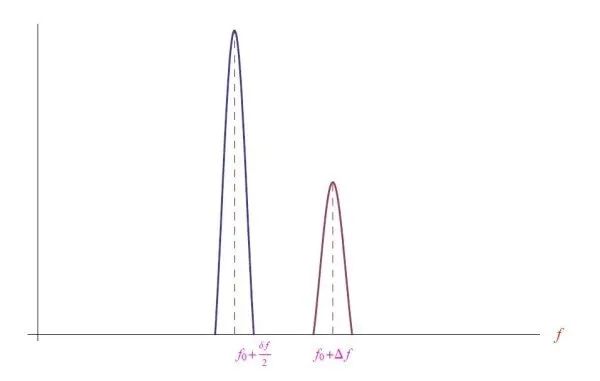 图5:目标的速度使得偏移频率落在传输频带之外
图5:目标的速度使得偏移频率落在传输频带之外
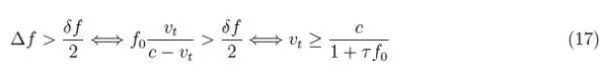

作者:Marcello Colozzo , 来源:EEWeb
参考原文:Sound Navigation And Ranging,由Ricardo Xie编译。版权声明:本文为电子技术设计原创文章,版权所有,未经授权,请勿转载。
 工作原理
工作原理
 图1:确定目标位置
图1:确定目标位置 最大距离
最大距离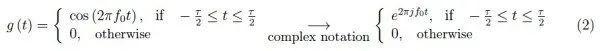
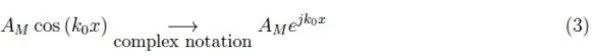

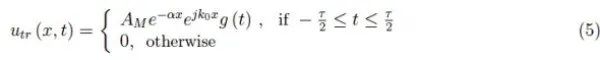


 图2:平面波的时间分量(5)
图2:平面波的时间分量(5) 图3:方程(2)的谱密度
图3:方程(2)的谱密度
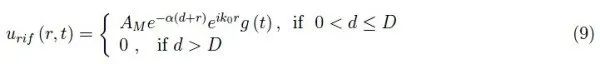
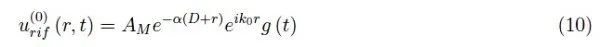
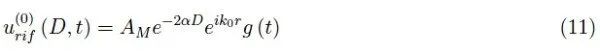
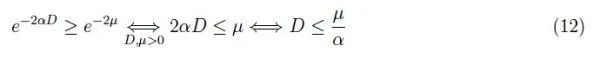

 脉冲传输频率
脉冲传输频率

 多普勒频移
多普勒频移
 图4:横向速度
图4:横向速度 图5:目标的速度使得偏移频率落在传输频带之外
图5:目标的速度使得偏移频率落在传输频带之外