正弦直方图方法测试模数转换器(ADC)

关键要点

• 使用正弦直方图测试方法可以确定模拟数字转换器（ADC）的参数，并优于线性斜坡直方图测试方法。

• 正弦直方图测试方法可以通过滤波器滤出正弦信号的谐波，提高线性度并增加测量精度。

• 正弦直方图测试方法能够更好地预测ADC在快速变化信号处理中的性能，并测量AC相关的错误。

摘要

本文介绍了如何使用正弦直方图测试方法来确定模拟数字转换器（ADC）的参数。相比线性斜坡直方图测试方法，正弦直方图测试方法具有更多的优势，包括能够滤除谐波和噪音，提高测量精度，以及能够更好地预测ADC在快速变化信号处理中的性能。文章详细介绍了正弦波的幅度分布、输出直方图的推导方法，以及如何使用正弦直方图方法来确定ADC的非线性和DNL误差。此外，文章还提供了有关非理想情况和阅读推荐的内容，以帮助读者更好地理解和应用正弦直方图测试方法来评估ADC的性能。

本系列的上一篇文章探讨了线性斜坡直方图测试在确定模数转换器 (ADC) 传递函数方面的有用性。这次，我们将重点关注正弦直方图测试。我们将首先讨论这种形式的直方图测试相对于线性斜坡方法的优势，然后通过方程式并使用正弦直方图方法来确定假设的 4 位 ADC 的非线性。

为什么要进行正弦直方图测试？

产生完美的线性斜坡输入是线性斜坡直方图测试的基本要求。输入信号中的任何非线性都会直接增加测量误差。这是一个问题，因为典型信号发生器产生的斜坡信号的线性度仅限于 8 至 10 位。

相比之下，我们可以滤除正弦信号的谐波，以获得比信号发生器提供的更高的线性度。该滤波器还可以抑制信号上的大部分噪声，以提高测量精度。对于斜坡输入，滤波器不能用于降噪，因为它会改变波形的形状。

在许多应用中，ADC 处理快速变化的信号。动态测试可以更好地预测此类应用中的 ADC 性能。高频正弦输入使我们能够测量 ADC 转换点，然后我们可以使用该转换点来评估 ADC 的交流相关误差（或动态性能）。虽然原则上我们可以使用高频斜坡输入来测量与交流相关的误差，但在较高频率下保持斜坡线性度变得更具挑战性。

正弦波的幅度分布

在线性斜坡直方图测试中，输入分布是均匀的。由于理想的 ADC 具有生成任何代码的相同概率，因此此功能使得分析斜坡直方图方法的测试结果变得非常简单。正弦波具有更复杂的分布，这反过来又使测试方程变得复杂。

让我们推导出正弦波产生的样本的概率密度函数 (PDF)，如下所示（图 1）。

图 1. 示例 ADC 的正弦交流输入。

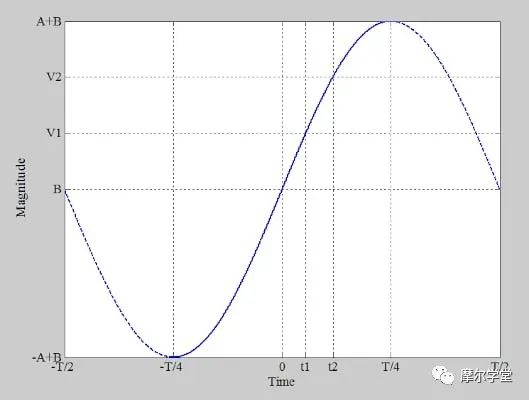
波形对应于以下等式：

在哪里：

A是信号的幅度

B是信号的偏移误差

f是正弦波的频率 (f
 = 1t)。

考虑 −T
4 到 -T4 范围内信号的半周期。这段时间内V IN落在V 1和V 2之间的概率是多少？通过将这两个值代入等式 1，我们可以创建以下等式，我们将使用该等式来查找相应的持续时间 ( t 2 – t 1 )：

等式2。

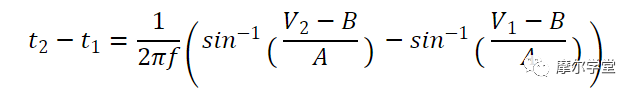
如果我们将该值除以总持续时间 (T
2)，我们就得到V IN落在V 1和V 2之间的概率：

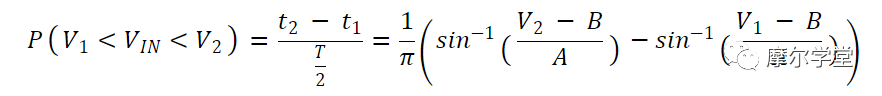
等式 3。

利用上面的表达式，我们可以推导出PDF函数。假设未知 PDF 函数为f ( V IN )，其积分为F ( V IN )。V IN位于V 1和V 2之间的概率如下：

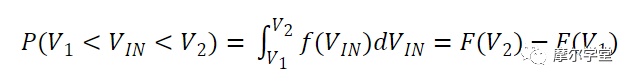
等式 4。

 如果我们比较公式 4 和公式 3，我们可以得出结论，PDF 函数的积分为：

等式 5。

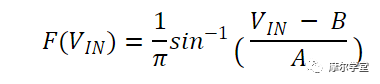
最后，对该函数求导，得到PDF函数：

等式 6。

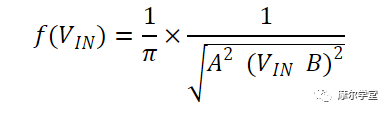
这些计算只考虑了信号的半个周期，但如果我们考虑一个完整的周期，我们仍然会得到公式 6。信号持续时间和V IN 在V 1至V 2范围内的持续时间都会加倍，因此我们最终会得到相同的结果。

在推导测试方程时，我们需要考虑到与斜坡输入不同，正弦波不具有均匀分布。为了进行直观演示，让我们看一下图 2 中的一对图。该图的顶部是公式 6 的图；下半部分是公式 6 的图。底部显示正弦波的旋转图。

图 2.上图：公式 6 的结果。下图：旋转的正弦波。

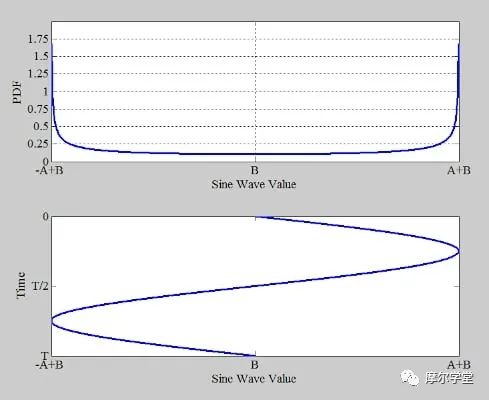
该图表明，正弦波过零附近的点出现的频率低于波峰和波谷附近的点。这是因为正弦波的变化率在过零处达到最大值，在波峰和波谷处达到最小值。因此，零交叉附近的样本不太可能出现。

导出输出直方图

现在我们已经生成了必要的方程，我们可以开始运行测试。我们将使用公式 3 为图 3 中的理想 4 位 ADC 构建输出直方图。请注意，公式 4 对于我们的目的同样有效 — 我只是选择使用公式 3 来进行此特定练习。

图 3. 4 位理想 ADC 传输函数。

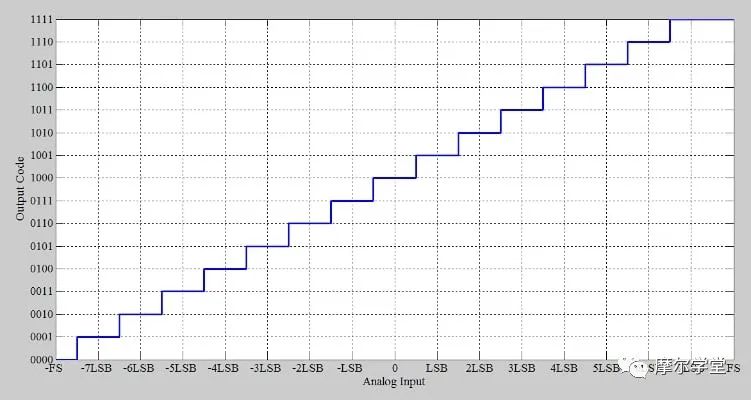
假设如下：

• 将振幅为A 的正弦波施加到 ADC。

• 正弦波没有偏移误差（B = 0）。

• 正弦波的幅度大于满量程电压。

因为正弦波两端超出了ADC的输入范围，所以我们可以确定输入执行了ADC的所有代码。

如果V LE表示上述传递函数左侧的第一个转变点，我们可以使用以下等式来找到其他转变点：

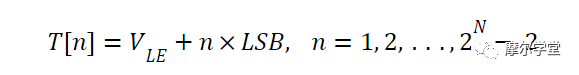
等式 7。

对应于代码 0001 的直方图 bin 的计数（用 H(1) 表示）与输入落在由V LE和 ( V LE + 1 LSB )界定的区域中的概率成正比。应用公式 3，我们得到：

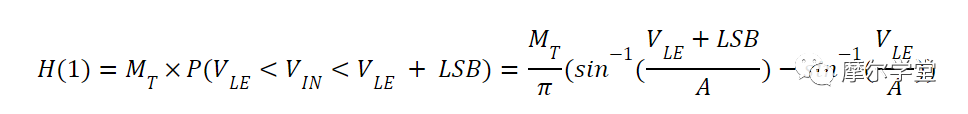
方程 8.

其中M T是捕获的样本总数。如果我们将方程 8 扩展到其他代码，我们可以导出 bin n计数的方程：

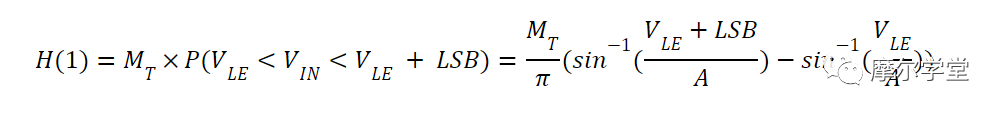方程 9.

为了验证这个方程，我们将使用图 3 中满量程电压为 1V 的传递函数来数字化具有以下特性的正弦波：

幅度 ( A ) = 1.1V

偏移误差 ( B ) = 0

频率 = 390.3 赫兹

我们将使用 40 kHz 的采样率。请注意，选择上述输入频率是为了不成为采样频率的分谐波；否则它是任意的。

通过收集 80,000 个样本，我们生成了图 4 中的直方图。红色曲线绘制了从公式 9 获得的值。

图 4.理想 ADC 的数字代码出现次数直方图。红色曲线显示公式 9 预测的值。

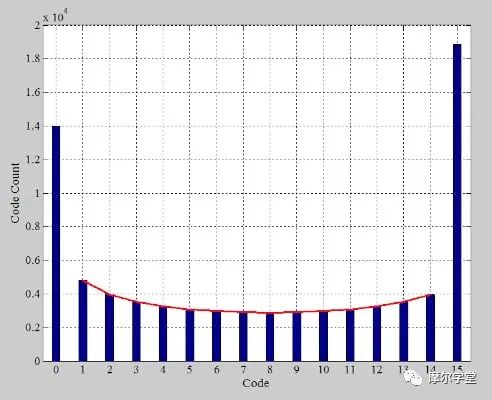
仿真结果与数学分析得到的值一致。为了帮助您更轻松地验证这一点，我在下表中提供了计算摘要。请注意，V LE = –0.9375。

表 1.计算和模拟结果总结。

数学分析预测的代码计数与模拟预测的代码计数接近，但不完全相同。这是因为直方图测试是一种统计方法。因此，更多的样本应该会提高测量的准确性。

使用正弦直方图方法查找 DNL 误差

考虑图 5（红色曲线）所示的非理想 4 位 ADC。

图 5.示例 ADC 的理想（蓝色）和非理想（红色）响应。

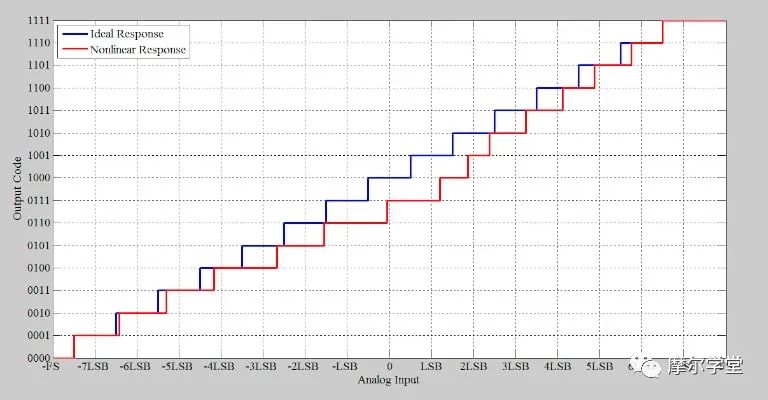
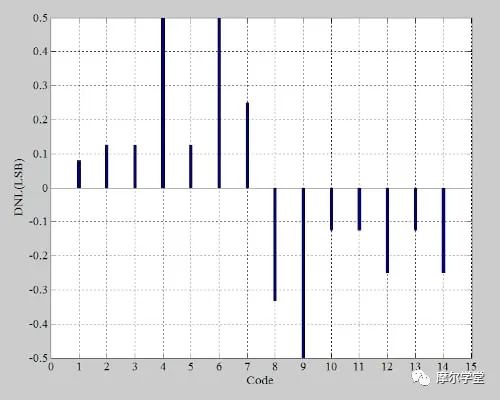
下面的图 6 中提供了该 ADC 的微分非线性 (DNL) 图。

图 6.非理想 4 位 ADC 的 DNL。

与上一节中的理想情况一样，我们将使用满量程电压为 1 V 的非线性传递函数以 40 kHz 的采样率对 390.3 Hz 正弦波进行数字化。同样如前所述，A = 1.1 V，B = 0。

请注意，图 5 中的传递函数没有失调误差或增益误差。因此，第一个和最后一个转换发生在其理想值 ( V LE = –0.9375)。收集 80,000 个样本，我们得到以下直方图（图 7）。

图 7.非理想示例 ADC 的数字代码出现次数直方图。

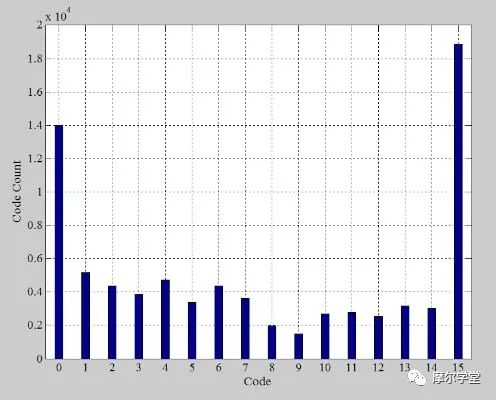
我们排除第一个和最后一个 bin，并将 bin 计数除以公式 9 给出的理想值。这给出了图 8 中的归一化直方图。

图 8.非理想示例 ADC 的数字代码出现次数的归一化直方图。

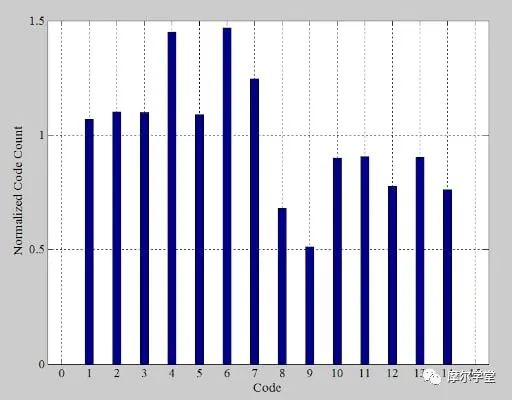
在标准化直方图中，理想的代码的 bin 计数为 1。因此，从 bin 计数中减去 1 会产生 DNL 信息，该信息由图 9 中的红色条形图绘制。蓝色条形图显示实际的 DNL 误差。

图 9.红色：示例 ADC 根据正弦直方图测试的 DNL 响应。蓝色：同一示例 ADC 的实际 DNL 响应。

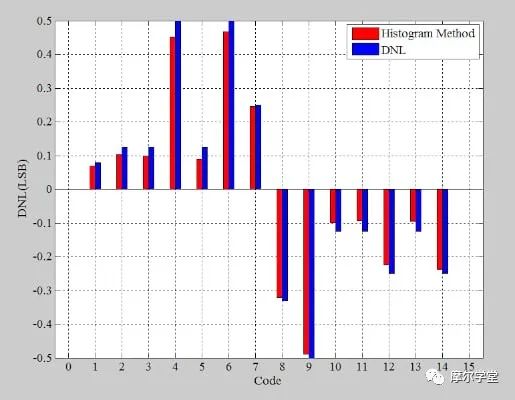
同样，直方图方法的结果接近实际值，但并不完全相同。正确选择不同的测试参数可以提高给定测试时间内的准确性。彻底分析不同测试参数对直方图方法准确性的影响是一个相对复杂的统计问题，涉及置信度、概率等因素。对于那些有兴趣更深入了解这些影响的人，我将在下一节中推荐一些进一步的阅读材料。

非理想性和阅读建议

在上面的示例中，我们使用了没有增益误差或偏移误差的理论 ADC。我们还使用了具有已知幅度和零偏移的正弦波。实际上，ADC 可能同时存在偏移误差和增益误差，并且我们可能不知道输入的确切幅度或偏移误差。这些非理想性会使归一化方程变得更加复杂。

要了解如何考虑这些影响，您可以参阅Mark Burns 和 Gordon W. Roberts 撰写的“混合信号 IC 测试和测量简介”。有关选择不同测试参数（例如所需的过载量和样本数量）的全面讨论，您可以参考J. Blair 的“使用正弦波进行 ADC 非线性的直方图测量”和“ A/D 的全速测试”转换器”作者：J. Doernberg、HS Lee 和 DA Hodges。

今天小编带来了：ISSCC2023套餐，里面有文章、Short Course、PPT、Tutorial等，同学可以拿回去自己学习研究。