一、浮点数如何存储
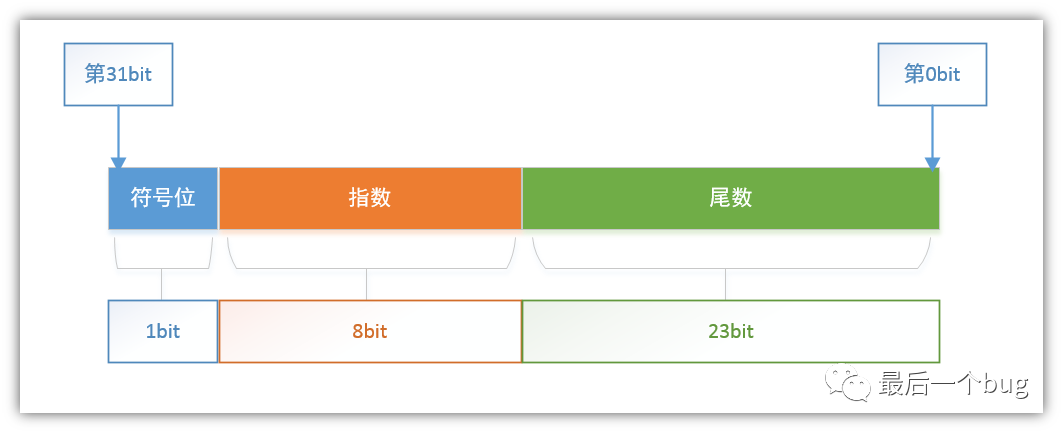
(符号:+/-)1.(二进制尾数)*2^(指数=实际指数+偏移量)
对于这几个名词不是特别好解释,结合实际转化过程会更加好理解。这里以float型浮点数:4.25为例子,如下转化示意图:
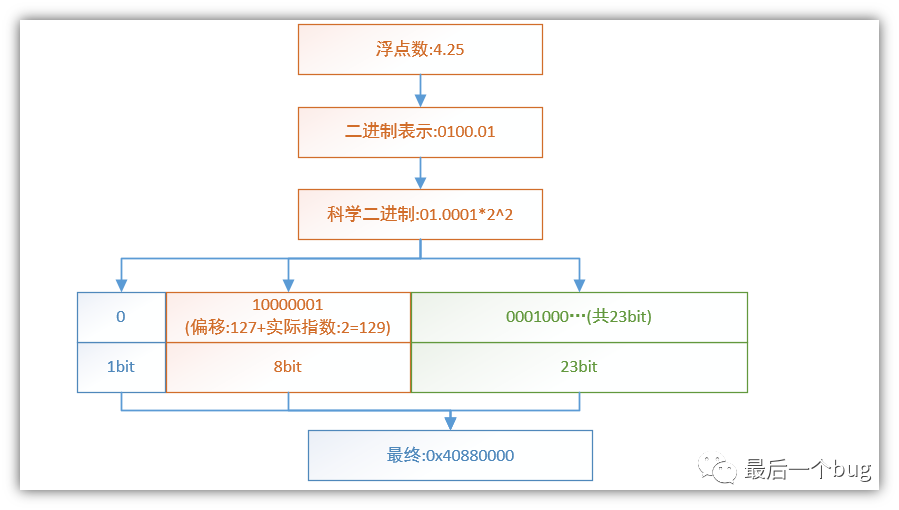
23bit的尾数部分前面0001即为科学二进制的小数点后面部分,其他bit用0填充;
指数部分会添加一个偏移量127,这个仅仅是对于float类型;对于其他浮点类型由于表示的数据范围不同偏移也不同,比如double需要+1023的偏移。
2、浮点精度问题
我们通过上面浮点数的存储方式可以知道8bit的指数最大可以表示255,最大值的指数就是255 - 127 = 128,2^128 = 3.402..e+38;(确实非常大!)
如果用我们的4byte无符号整形表示最大数据为2^32,看起来远远小于浮点表示;不过大家是否想过一个问题,根据数据二进制一一对应原则都是4byte的表示方法为什么有这么大差异,难道浮点数凭空创造了更多的数据吗?
非也非也,指数部分代表着浮点数的范围,尾数部分代表着浮点数的精度;我们从尾数的角度来看,浮点的二进制科学计数法小数点前始终是最高位,这也就意味指数越大,尾数部分所表示的数值越大,其精度越差。
所以,float与uint表示的数据个数都是一样的,整形表示的数据是均匀的,而浮点表示的数据在数值比较小的时候精度比较高,而数值比较大的时候就比较低了;同时也说明浮点表示仅仅是一种近似的表示方法,不能精确的表示数值,所以有时候大家在编程的过程中明明向float类型变量赋值了一个准确的数据,仿真一看数据成了一个近似值。
3、浮点与"=="
这个问题也是大家经常讨论的,不过还是需要具体情况具体分析,到底浮点数能不能用等于号来进行判断呢?首先我们看看什么叫相等,相等就是一模一样,对于计算机而言就是二进制相等,否则我们只能叫近似。
前面我们了解到了浮点的存储形式,如果两个浮点的三个部分都是相等的(符号位+指数+尾数),那么这个时候,这两个浮点数就是绝对的相等,如果不能达到完全相等就只能使用近似判断相等,比如我们常用下面的方式来表示:
/***************************************
*Author:(公众号:最后一个bug)
****************************************/
#define FLOAT_EPS (0.000001) //根据需求
#define Float_Equ(a, b) ((fabs((a)-(b)))<(FLOAT_EPS))
不过,对于浮点数相等大家尽量还是减少使用,较多浮点运算控制器都会有不同的处理方式,比如说扩展精度、截取尾数等等,对于代码的可移植性减弱。
二、玩转浮点数
代码走起~
#include
#include
typedef union _tag_FloatConvert
{
unsigned char byte[4];
float Result;
}uFloatConvert;
/*****************************************
* Fuction: main
* Author :(公众号:最后一个bug)
*****************************************/
int main(int argc, char *argv[]) {
uFloatConvert unFloatConvert;
float fVal = 4.25;
int iVal = 0x40880000;
float *pfVal = NULL;
int *pIVal = NULL;
//1)初学组拼数据经常的错误
fVal = (float)iVal;
printf("*fVal = %.3f\n",fVal);
printf("iVal = %d\n",iVal);
//2) 正确组拼数据
pfVal = (float*)(&iVal);
printf("*pfVal = %.3f\n",*pfVal);
//3)采用共联体进行数据转化(方便)--大家以后可以封装成函数
unFloatConvert.byte[0] = 0x00;
unFloatConvert.byte[1] = 0x00;
unFloatConvert.byte[2] = 0x88;
unFloatConvert.byte[3] = 0x40;
printf("unFloatConvert.Result = %.3f\n",unFloatConvert.Result);
printf("公众号:最后一个bug\n");
return 0;
}

END
→点关注,不迷路←