这是一个常见到的多谐振荡电路,简单而优雅。大家注意到,在LTSpice 仿真软件中搭建的这个仿真电路中,R2,R3的阻值稍微相差一点点。这是为了能够使得电路能够震荡起来。·如果这个电路左右器件参数都是一样的,-那么该电路就无法起振了。今天通过仿真实验,验证一下这个电路的工作频率随着电源电压之间的变化关系。根据近似的分析方法,这个电路振荡频率与电路的工作电压没有关系,只和电路中耦合电容以及三极管基极配置电阻的组织有关系。所以通常来讲,工作电压对于电路的振荡频率没有影响。
为了仿真电源对电路影响,电源参数,被设置成从0V线性上升到20V的变化电源,上升时间为 1秒钟。观察震荡晶体管的集电极和基极的震荡电压波形。这是仿真获得的电路震荡电压信号。上面是集电极电压信号,随着振荡电路工作电压增加,震荡信号的幅值也随之线性增加。基极反向偏置电压幅值也是随着工作电压增加而上升。只是,在真实的三极管电路中,基极反向偏置电压会受到三极管基极反向击穿电压的限制,当大于反向击穿电压制后,基极电压信号就会维持在一个固定的数值了。
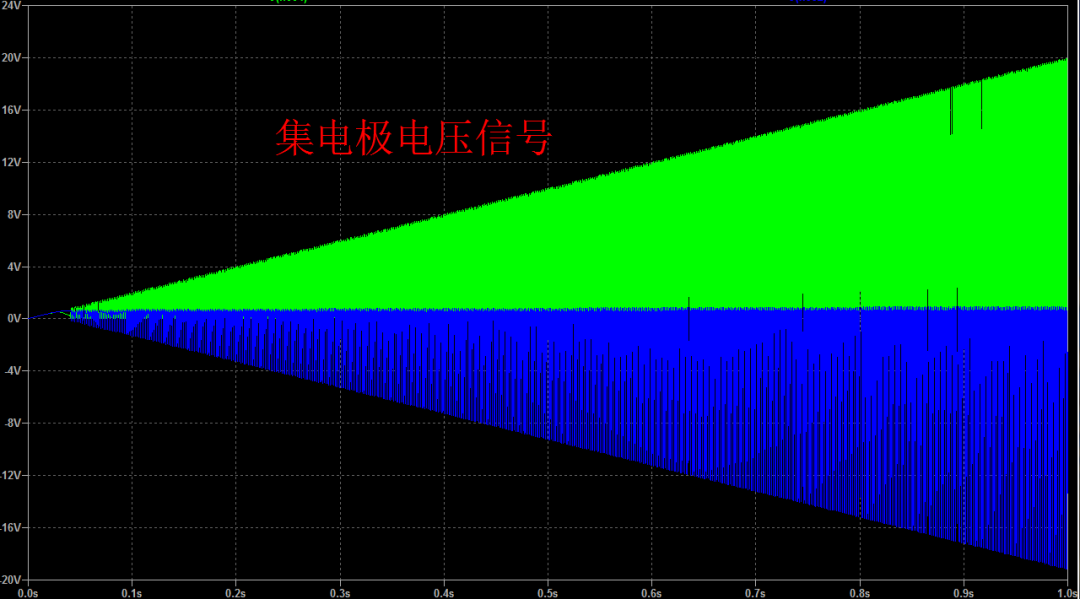
下面将震荡波形放大来看。可以看到集电极和基极信号变化有很大的区别。集电极信号一开始的上升是由集电极负载电阻在耦合电容上充电过程,充电过程非常快,很快就基本上充电到电源电压。晶体管饱和时,对应的集电极低电平只有大约 0.1 V左右。蓝色波形是晶体管基极电压信号,基极反向偏置电压,使得晶体管截止。这个电压下降幅值,实际上是晶体管集电极电压下降经过耦合电容施加在基极上的。这个充电过程是由基极电阻在耦合电容上充电过程,这个充电时间决定了振荡电路的半个周期,一般情况下,这个时间可以近似表达为 log(2) 乘以 Rb Rc。与电路的工作电压无关。
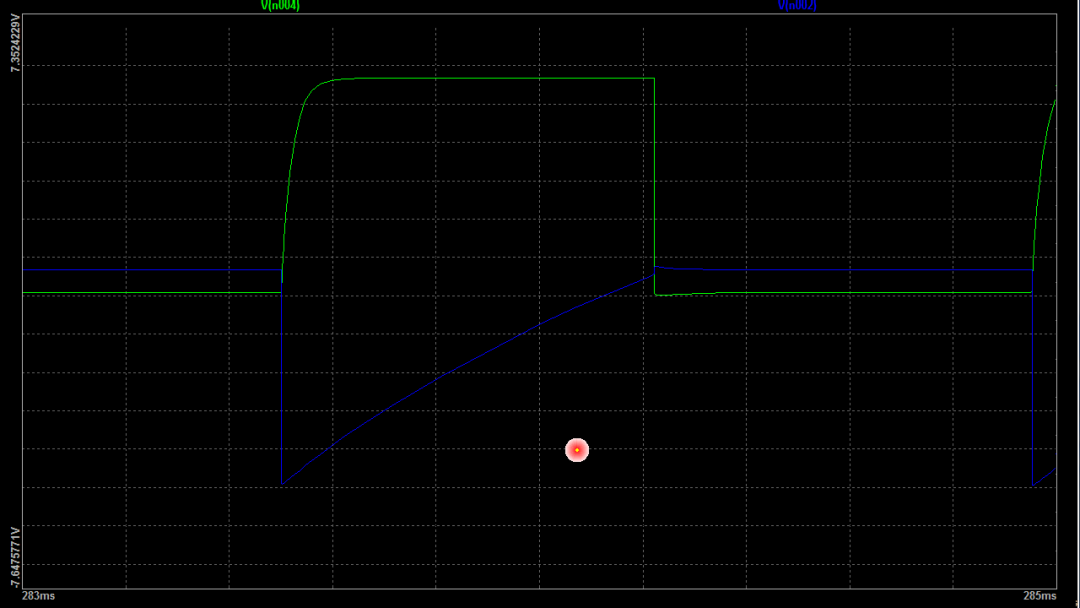
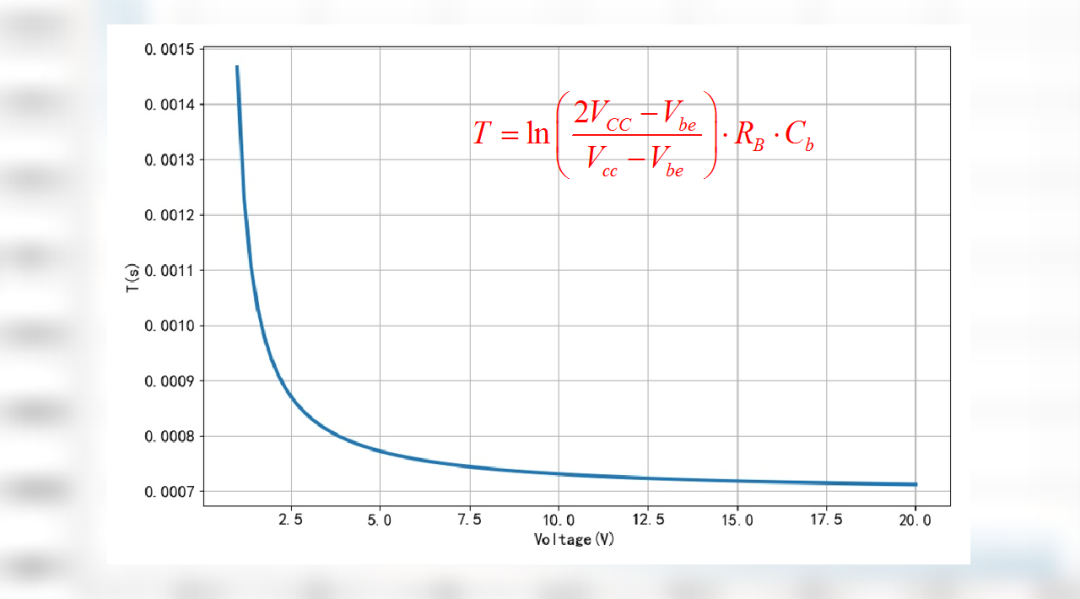
▲ 图1.3.1 放大之后的震荡波形但是,如果考虑到基极的偏置电压 Vbe 的影响,大约为 0.7V。那么这个充电过程的时间就会有变化。充电的终值近似为工作电压 Vcc。充电起始电压为 Vcc 减去 Vbe。电路翻转电压,近似为基极偏执电压 Vbe。那么根据RC充电公式,可以知道对应的充电时间。这个时间就与 Vcc 有关系了。如果 Vbe近似等于0,那么这个公式就退化为上面的近似公式。
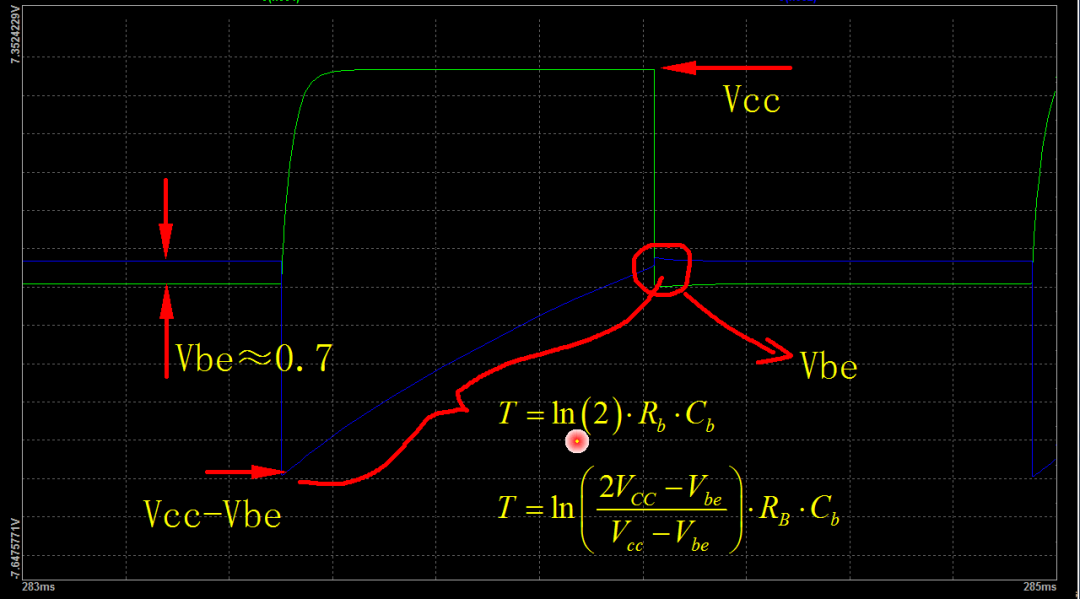
下面根据电路中实际电阻电容参数,绘制出电路工作电压从 1V 变化到 20V时,对应的震荡半周期变化,可以看到电路震荡周期随着工作电压的升高而下降,对应的振荡频率反过来也会随着工作电压上升而上升。
这是根据仿真波形直接计算出震荡周期的变化关系。因为仿真工作电压也是从0V线性增加到 20V,所以这个曲线也反映了多谐振荡电路震荡周期与电源电压之间的关系。这是电路振荡周期,所以比起前面计算的时间要大一倍。但整体变化趋势它们是一致的。这也验证了前面理论分析的正确性。
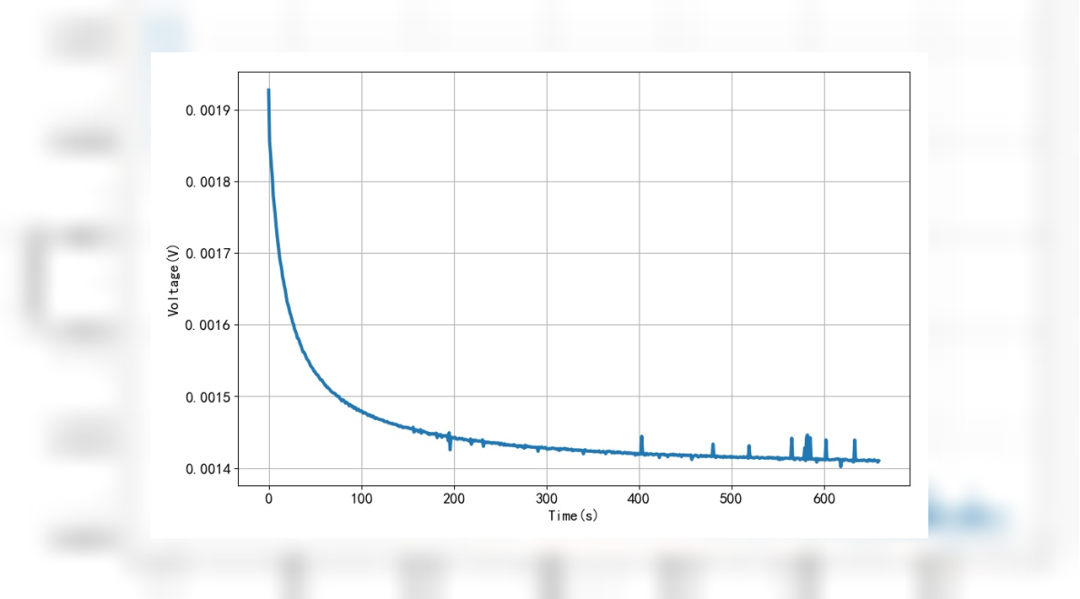
本文分析了多谐振荡电路震荡周期与工作电源之间的关系。仿真实验数据验证了理论分析的正确性。
