我零散地玩了十几年电路,又以音频放大为主,看到过也实验过一些有意思的电路结构,很久以来就有想法要和大家分享。这次要分析的是放大电路中的自举电路。作为一个没有上过一门电子学课,靠兴趣自学过来的DIYer,我若下面讲的内容有错,请各位老师斧正!
“自举”(翻译自bootstrap)这个词汇在多个领域可能见到(字面意思是提着靴子上的带子把自己提起来,这当然不可能),在电路里面,这是一个古老的技术。而且自举也不仅是在放大电路中,例如在电源里面也用到自举,但本人了解不多就不在此讨论了。
音频功率放大器中的自举电容

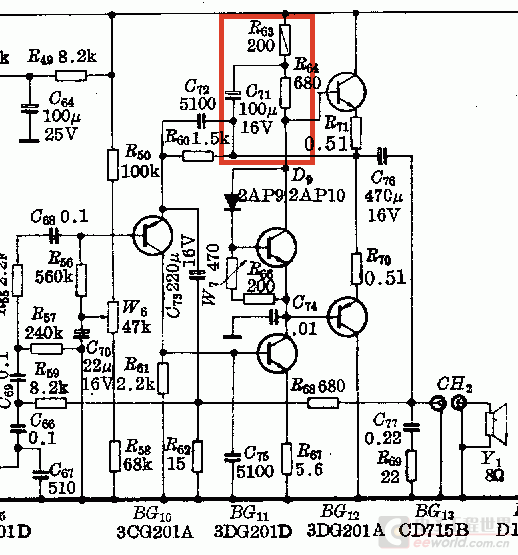
这个自举电路是我最早见到的自举,在古老的分立半导体收音机功率放大部分经常见到(相比用输入输出变压器的那种,其实也还不那么老了,不过收音机早都用集成电路了),就像下图中红框标出的部分这样。
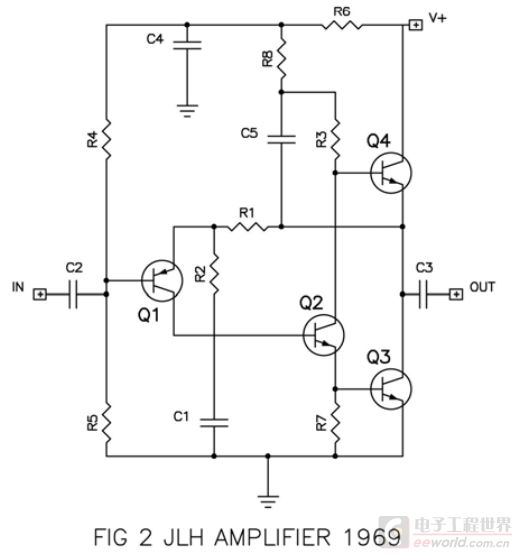
又如,在经典的 JLH 1969 功放电路里面(下图中 R3, R8, C5 构成自举):
不过上面两个电路都包含了负反馈,倘若再弄得简单一些(不实用)来分析,就成下面我画的这个电路了:
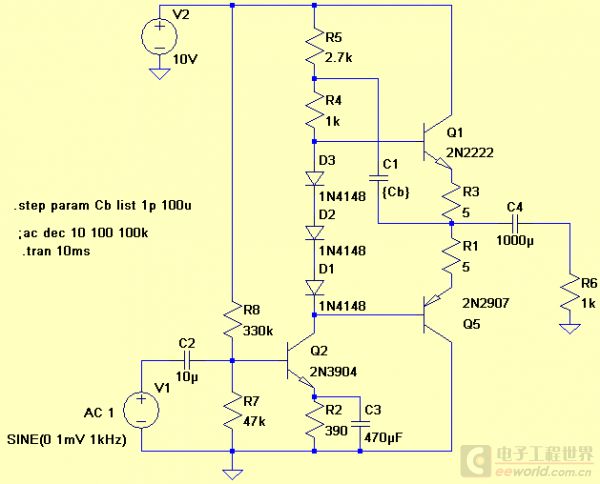
这个电路是一级共发射极放大(Q2),加上一级互补射极输出器(Q1, Q5)。如果先忽略自举电容C1,那么 R4串联R5 一起构成了 Q2 的集电极负载电阻(3.7k)。当然计算Q2电压增益的时候还要把 Q1/Q5 的输入阻抗考虑进去。Q2这一级电压放大的增益和集电极负载阻抗大致是成正比的(这里暂不考虑Miller效应、Early效应),如果后面射极跟随器的输入阻抗足够高的话,也就成了集电极负载电阻越大,增益越大了。可是把直流工作点考虑进来,要想集电极负载电阻越大而集电极电流不变的话,就要提高电源电压……所以集电极负载电阻选择受限。
好了,现在把集电极负载电阻拆成两段,加进来一个自举电容,形成上面的样子,直流工作点不变。现在Q2集电极负载电阻是多少?R4么?似乎不对。看时域仿真分析吧:
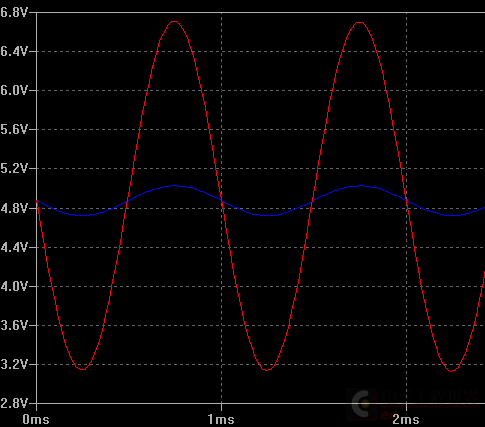
仿真所示输出节点(R3, R1公共端)的电压波形: 100uF 自举电容加入以后(红色线),输出信号幅度比不加电容时(蓝色线)大了一个数量级。
为什么会有这样的效果?上面电路中负载电阻 R4 一端接在Q1的集电极(按交流等效,忽略三个二极管上压降的变化),也是射极输出器的输入,另一端经过自举电容接在射极输出器的输出。因为射极输出器是同相放大,电压增益略小于但接近于1,这是一种正反馈的接法。将上面电路自举起作用的部分摘出来,画成下图:
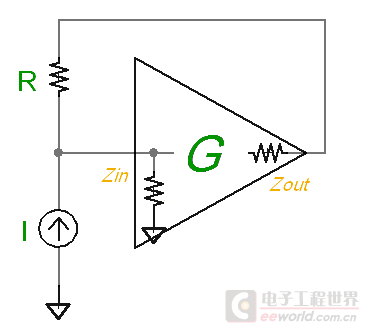
第一级晶体管的输出看成是一个电流源,射极输出器相当于一个增益G约等于1的放大器,它有很高的输入阻抗 Zin 和较低的输出阻抗 Zout. 这里把自举电容的阻抗也合并到 Zout 中。虽然在上面完整电路里面自举电容还接了一个电阻到电源(交流等效地),利用戴维南定理将它等效到放大器中(导致增益下降)。第一级晶体管的输出阻抗和 Zin 是并联关系,可以合并看待。
如上的简化处理之后,电路的增益就不难计算了。根据电流平衡,可以解得放大器输入端的电压是
I*(R+Zout)*Zin/[Zin*(1-G)+R+Zout] = I*[(R+Zout)/(1-G)*Zin]/[Zin + (R+Zout)/(1-G)]
也就是,从第一级晶体管输出端看到的负载阻抗是 (R+Zout)/(1-G) 和 Zin 并联的值。换句话说,自举这一技巧使集电极负载电阻约被“增大”了 1/(1-G) 倍。
不妨再用 spice 仿真验证一下,如下:
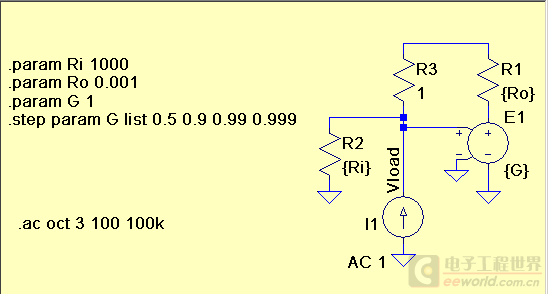
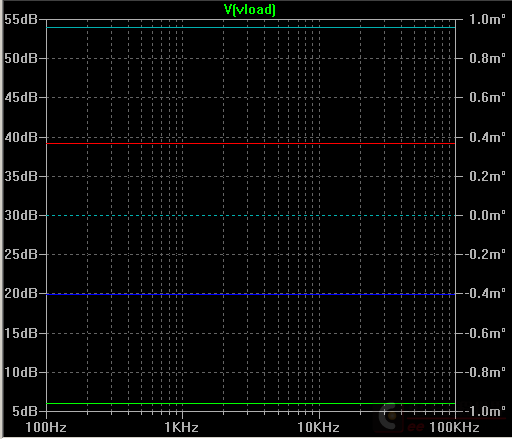
当 G 分别为 0.5, 0.9, 0.99, 0.999 时,电阻被“放大”了2, 10, 100, 1000 倍,导致增益提升 6dB, 20dB, 39dB, 54dB (受到Zin限制,增益不能无限提高)。
最后还有一个小问题:实际的功率放大电路中有负反馈控制了总的增益,那么自举电路是否还起到明显的作用?实际上,负反馈引起闭环增益的下降,是使得前面共发射极电路的输入幅度降低,而单独看这一级的增益仍然是因为自举电路而提升的。开环增益提高使闭环后的频率响应和失真率都改善更多,因此在以前功率放大器中常见这样的电路。
利用自举提升输入阻抗

再把上面电路中的共发射极放大部分忽略,单独看射极输出器呢?哦,电路缺了点啥——需要给射极输出器加上偏置啊。偏置电阻也会成为输入信号的负载,使整个跟随器的输入阻抗降低。不过,将自举电路的接法变形一下,成下面这样之后……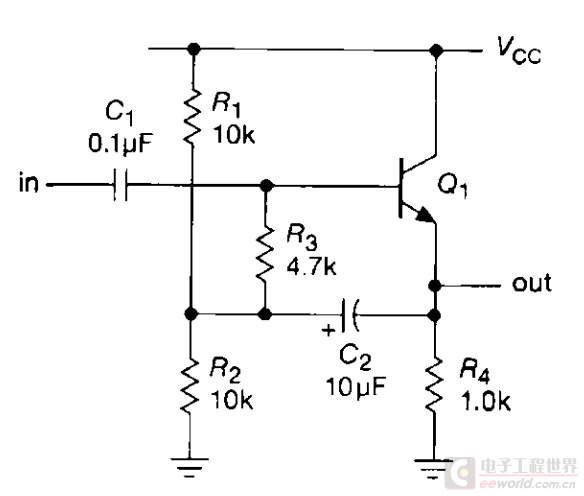
用刚才推导的“电阻倍增”原理,这个电路里面输入偏置电阻从原来的 R3+R1//R2 变为了 (1-G)*R3,对输入阻抗的影响就消除了。不过要进一步提高输入阻抗,Q1的负载需要减轻。下图是 Douglas Self 书里面里讨论高输入阻抗电路时的一个例子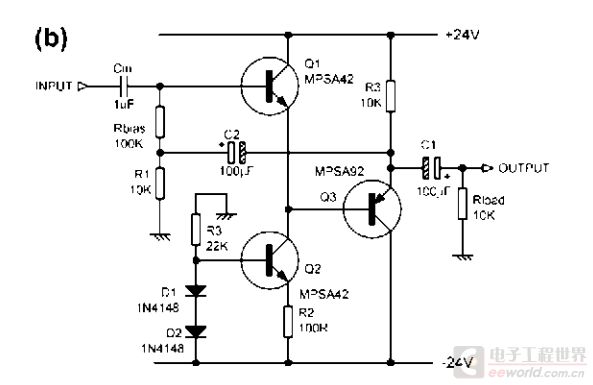
这个图上有两级跟随器,自举电容是从第二级后取出信号的,可以认为这样总增益更接近于1,而且第一个管子的输入阻抗也提高了。
交叉射级输出器中的自举电容

这个四管的两级射极输出器电路是我从黑田彻(日)的书上学来的,在我制作的一个耳机放大器模块中使用了。
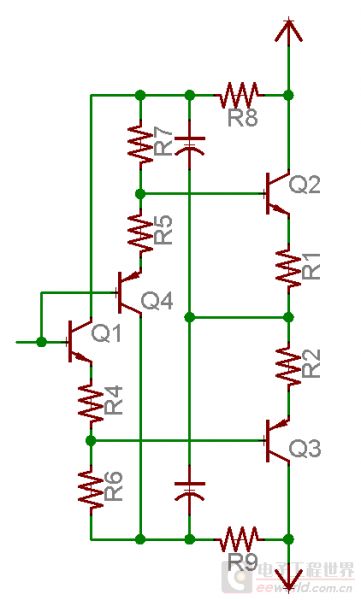
和第一个经典的自举电路有几分相似,作用却不尽相同。首先,按照前面的结论,R4+R6,以及 R5+R7 分别被“倍增”了,等效阻抗提高。注意,Q1 是射极输出器,R4+R6现在是 Q1 的发射极电阻,当它被等效放得很大,就相当于 Q1 发射极接了一个恒流源。同时,自举电容也改变了 Q1, Q4 的集电极交流电位,使 VCE 几乎恒定——这样的好处是大大消除了晶体管集电结电容的影响,在这个电路中减小了输入电容,提升高频性能。
小结一下,到目前我们看到了自举电路的几个用法:
(a) 提高共发射极放大电路的增益(也可以用在共基极放大电路)
(b) 提高射极输出器(跟随器,共集电极电路)的输入阻抗
(c) 稳定射极输出器的发射极电流
(d) 使射极输出器的集电极电压跟随发射极
以上电路共同特点是:
(1) 从射极输出器(电压增益约为1)的输出用自举电容引出信号,馈送到它的前级
(2) 从低阻节点向高阻节点的反馈,自举电容只有一端是强驱动(电压输出)信号
省去自举电容

自举电容的作用是隔直流,即只对交流信号有效,采取自举后不改变直流工作点。倘若工作点选择合适,也可以不用自举电容实现自举,如下面这个电路:
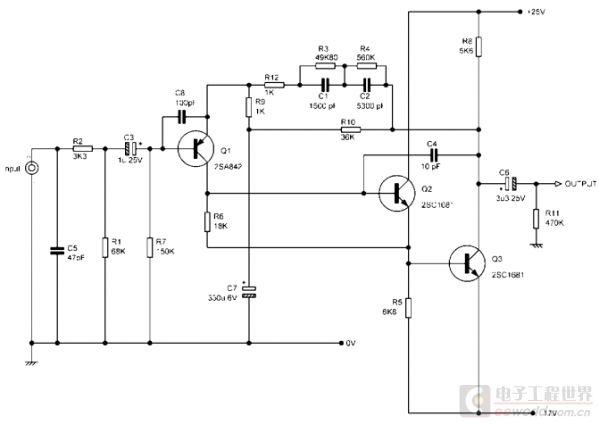
注意 R6 的接法,它是否被自举“倍增”了?
用运放替换射极输出器

自举电路中增益约等于1的放大器,除了用射极输出器实现,也可以用源极输出器、运放缓冲电路等实现。下面电路中电位器用来调整反馈比例,也就是等效于改变增益,从而使电阻“倍增”的倍数可调,实现可调的滤波器。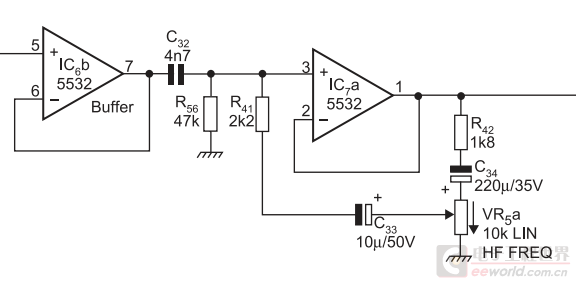
IC7a, 连同 R42, VR5a 构成自举中的放大器,C33是自举电容,使 R41 等效“加倍”。注意,这个“倍数”与VR5a并不是成线形关系的,猜想是特意为之,不然不用自举电路,直接把R41换成电位器了。
再看一个复杂一点的,不那么明显的电路 (pdf里面的图就是这么不清楚了,没办法):
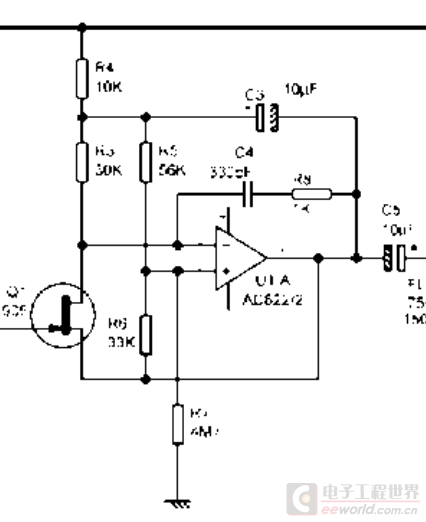
除了一个与电容串联的电阻用在频率补偿,其余几个电阻是为了设置直流工作点的,与增益无关。从JFET的栅极到运放输出,电压增益为1,注意,由于运放强大的开环增益,对交流信号来说JFET的 G, D, S极都是等电位的。由于运放自举的作用,是管子的电流几乎不变,D-S端电压也几乎不变。在这个电路里,自举用来实现很高的输入阻抗。
以上的自举电路中,关键部分——放大器(提供电流的缓冲器)的输出也是信号的输出。好象是添加少量阻容元件就增加了自举功能。下面将要介绍的是,用缓冲器仅仅为了自举,而不输出信号的电路。
场效应管的自举 Cascode

这是我个人很喜欢的电路,下图是我做过的一个放大器的差分输入级,在两个JFET上使用了自举。
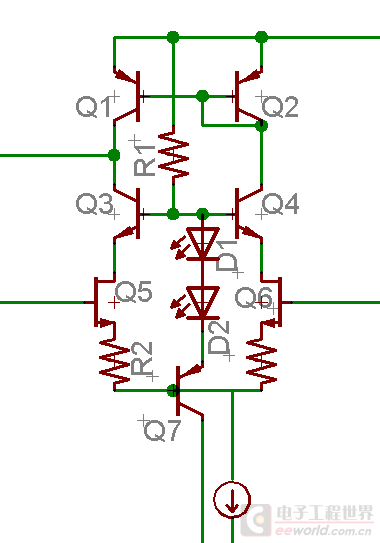
这个电路中 Q5 Q6 两个管子是差分放大,静态电流由源极的公共电流源决定。Q1 Q2组成镜像电流源负载,是很常见的电路接法。Q3 和 Q4 是用来自举的,它们的基极跟随 Q5 Q6 的源极电压变化,因此发射极也跟随 Q5 Q6 的源极电压变化。这个自举电路的目的是让 Q1 Q2 的 VDS 保持恒定,从而消除寄生电容 Cgd 的影响(因为JFET这个电容比较大,是缺点)。R1, D1, D2, Q7 在这里的作用是利用二极管的稳压特性提供一个基本不变的偏置电压。
在此处,如果将 Q3, Q4 看作缓冲器,那么它们输出的信号并没有被引出来使用,只是用来确定 Q5 Q6 的漏极电压了。然而 Q3 Q4 的确是输出了信号的,是从集电极输出的——应用时增益远大于1了。拆开来看,Q3-Q5, Q4-Q6 都是 Cascode 电路,只不过共基极放大部分的基极电压随着差分对管而变动了——所以是自举式的 Cascode.
上面电路中Cascode的共基极三极管偏置方式稍微复杂了点,如果换成适当的JFET,可以使这个Cascode很简洁,如下面这样。
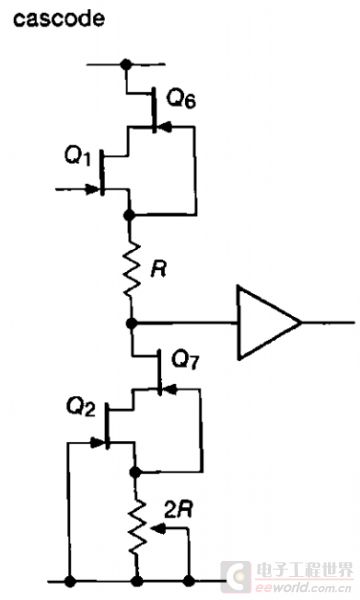
这种接法对 JFET 的选择有所限制,不是随便抓两个管子就行。因为需要保证在设定的电流下,输入信号的那个管子(上图 Q1 Q2)VDS 等于它上面那个自举用的管子的 VGS.
运放电源自举

最后来看一种特殊的自举用法:改变运算放大器的电源电压,让两个电源端跟随输入端而动。这样在那个被自举的运放看来,好象+端输入信号恒定一样——也就是消除了输入共模电压。这个技巧被用来减少运放输入级的失真。
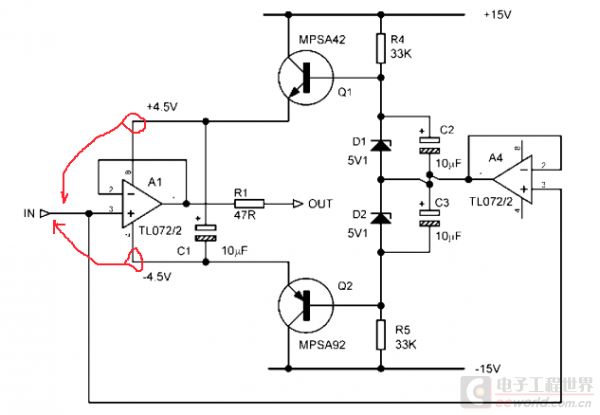
如上图,电源自举付出的代价是不小的,除了增加一个运放作为跟随器外,还因为需要提供大电流使用了两个晶体管扩流。
总结归纳一下上面例子电路中“自举”的要点:有一个提供低阻抗输出的缓冲器(增益约等于1的放大器),它将参考节点的电压缓冲后施加到电路中另外的某个节点,使其交流电压随着参考接点作相同的变化。结果是在某些元件或者部分电路的端子上产生恒压之效,提升电路的某方面性能。
推荐阅读